Guia de Interação
Plano de Aula
Plano de aula: Translações no plano
Plano 2 de uma sequência de 5 planos. Veja todos os planos sobre Simetrias
Tem interesse no tema "Neurociência, adolescências e engajamento nos Anos Finais"?
Inscreva-se neste tema para receber novidades pelo site e por email.
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Marcia Maria Viana Suriano
Mentor: Renata S. Gonçalves
Especialista de área: Pricilla Mendes Cerqueira
Objetivos específicos
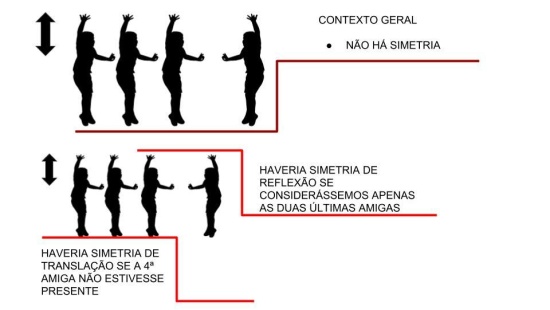
- Construir o conceito de simetria de translação;
- Estudar a movimentação de polígonos no plano cartesiano, trabalhando a sua posição original e localização da forma após transformações.
Conceito-chave
Simetria de translação
Recursos necessários
Folha de atividades impressa, cartões numerados conforme anexo da atividade, Datashow (opcional)
Leitura Complementar
Geometria das transformações. Disponível em: <https://novaescola.org.br/conteudo/2711/geometria-das-transformacoes> Acesso em: 06/02/2018
Habilidades BNCC:
Objetivos de aprendizagem
- Construir o conceito de simetria de translação;
- Estudar a movimentação de polígonos no plano cartesiano, trabalhando a sua posição original e localização da forma após transformações.

Precisa de ajuda para criar uma aula personalizada?
Crie seu plano de aula em menos de um minuto no WhatsApp.
Novo curso gratuito

Conheça nosso mais novo curso sobre adolescências, neurociência e engajamento nos anos finais
VER CURSO