Atividade Principal
Plano de Aula
Plano de aula: Aplicando frações como operador em diferentes contextos
Plano 4 de uma sequência de 5 planos. Veja todos os planos sobre As frações em nosso dia a dia
Por: Luiz Filipe Trovão
Tem interesse no tema "Neurociência, adolescências e engajamento nos Anos Finais"?
Inscreva-se neste tema para receber novidades pelo site e por email.
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Luiz Filipe Trovão
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA06 - Reconhecer que as resoluções de um grupo de problemas que têm a mesma estrutura podem ser obtidas utilizando os mesmo procedimentos.
EF07MA08 - Comparar e ordenar frações associadas às ideias de partes de inteiros, resultado da divisão, razão e operador.
EF07MA09 - Utilizar, na resolução de problemas, a associação entre razão e fração, como a fração 2/3 para expressar a razão de duas partes de uma grandeza para três partes da mesma ou três partes de outra grandeza.
Objetivos específicos
- Efetuar multiplicações envolvendo uma fração e um número natural;
- Realizar uma análise de várias situações problema envolvendo o uso de frações como operador.
Conceito-chave
Multiplicação de uma fração por um número natural; Fração como operador.
Recursos necessários
Lápis, borracha e caderno.
Habilidades BNCC:
Objetivos de aprendizagem
- Efetuar multiplicações envolvendo uma fração e um número natural;
- Realizar uma análise de várias situações problema envolvendo o uso de frações como operador.
Planeje suas aulas pelo Whatsapp!
Qualidade com economia de tempo
Aula
Resumo da aula
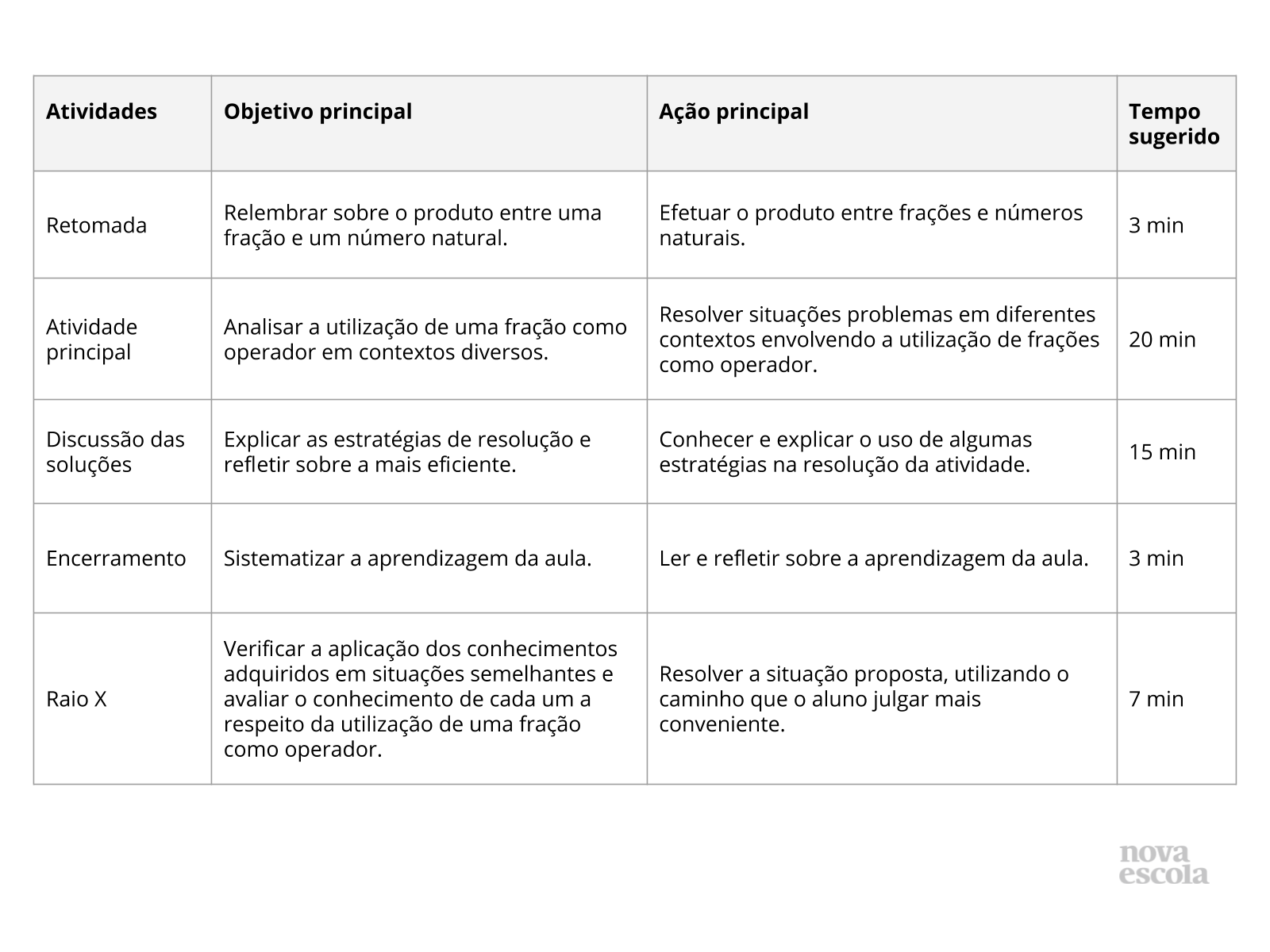
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Materiais complementares:
Acesse o arquivo sobre o plano aqui.
Leituras:
- Nova ordem numérica: https://novaescola.org.br/conteudo/2657/nova-ordem-numerica
- Introdução aos números racionais: https://novaescola.org.br/conteudo/2722/introducao-aos-numeros-racionais
- Dividir as dúvidas para compreender as frações: https://novaescola.org.br/conteudo/2135/dividir-as-duvidas-para-compreender-as-fracoes
Objetivo
Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma. Caso não seja possível a projeção, escreva o objetivo no quadro.
Propósito: Compartilhar o objetivo da aula.
Novo curso gratuito
Conheça nosso mais novo curso sobre adolescências, neurociência e engajamento nos anos finais
VER CURSO
