Guia do Intervenção
Plano de Aula
Plano de aula: Classificação dos poliedros pela base
Plano 7 de uma sequência de 10 planos. Veja todos os planos sobre Prismas, pirâmides e suas planificações
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Maria Carolina Taurisano
Mentor: Paula Massi Reis Pires Pires
Especialista de área: Priscilla Mendes Cerqueira
Habilidade da BNCC
(EF04MA17) Associar prismas e pirâmides a suas planificações e analisar, nomear e comparar seus atributos, estabelecendo relações entre as representações planas e espaciais.
Objetivos específicos
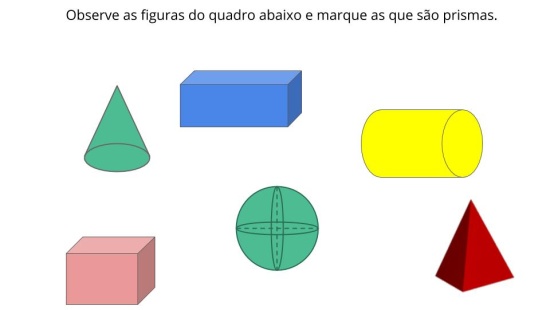
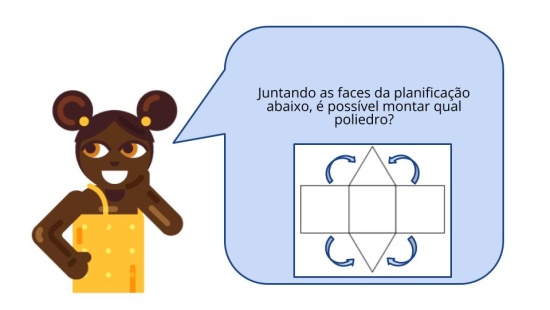
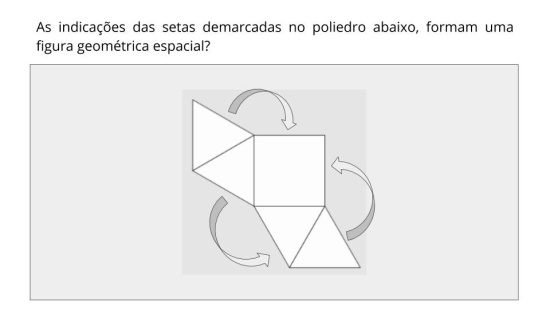
Localizar a base dos poliedros e investigar a possibilidade de classificá-los por meio da base representada.
Conceito-chave
Base de poliedros.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não.
Habilidades BNCC:
Objetivos de aprendizagem
Localizar a base dos poliedros e investigar a possibilidade de classificá-los por meio da base representada.

Precisa de ajuda para criar uma aula personalizada?
Crie seu plano de aula em menos de um minuto no WhatsApp.