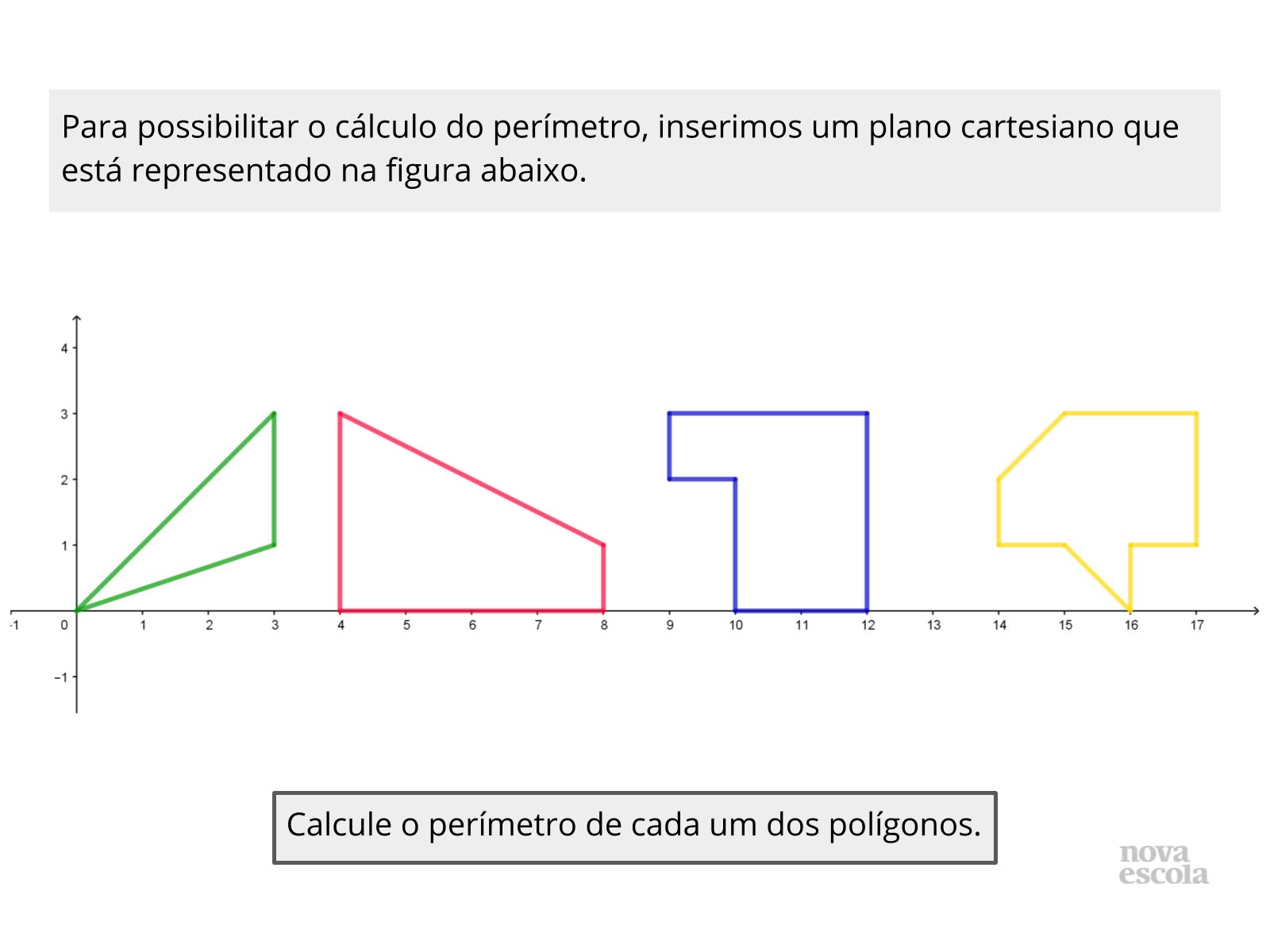
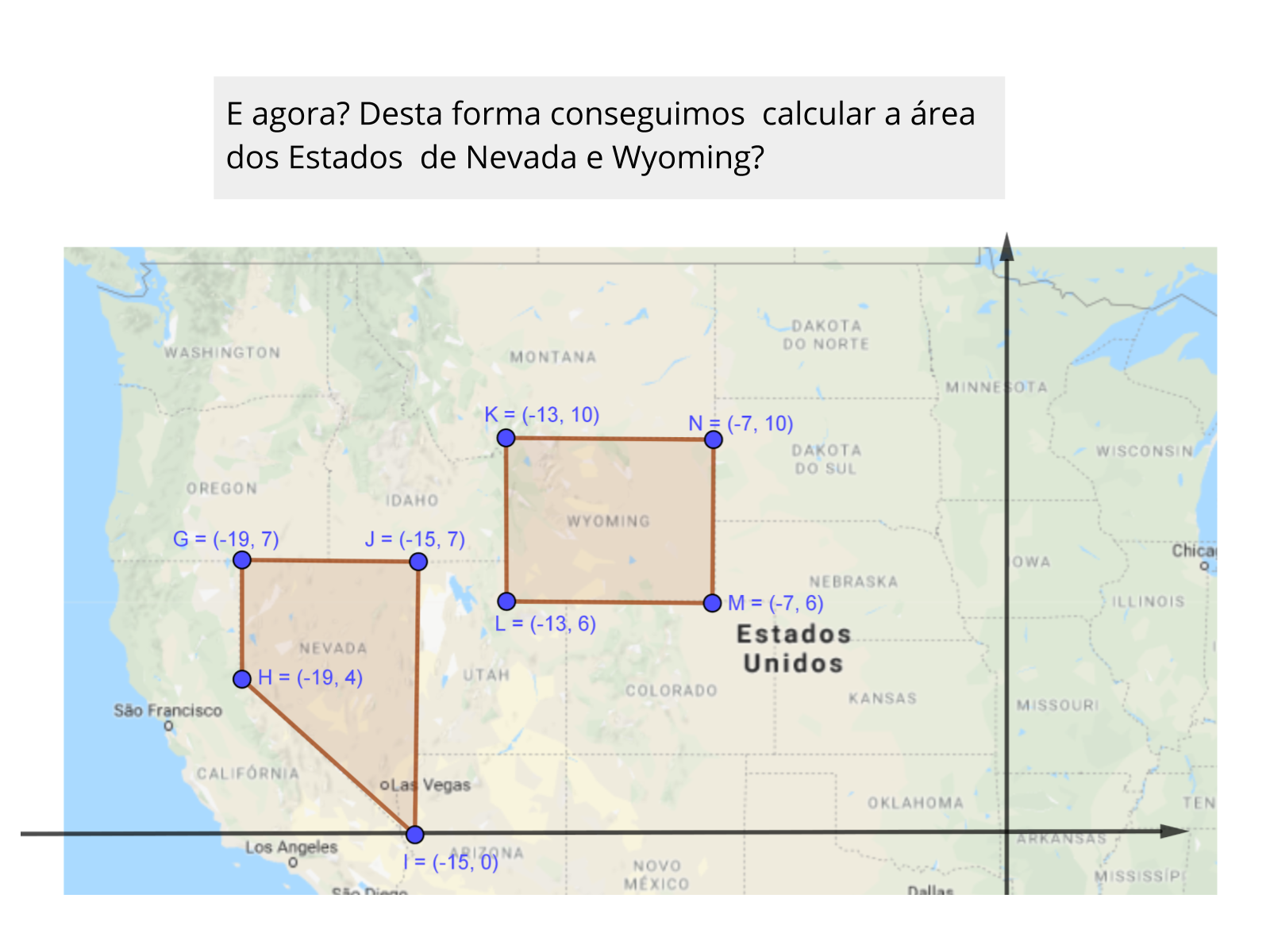
Resolução da Atividade de Retomada
Plano de Aula
Plano de aula: Encontrando o ponto médio de um segmento
Plano 2 de uma sequência de 5 planos. Veja todos os planos sobre Distância entre dois pontos no plano cartesiano
Tem interesse no tema "Neurociência, adolescências e engajamento nos Anos Finais"?
Inscreva-se neste tema para receber novidades pelo site e por email.
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Rodrigo de Melo Pessanha
Mentor: Lara Martins Barbosa
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
(EF09MA15) - Determinar o ponto médio de um segmento de reta e a distância entre dois pontos quaisquer no plano cartesiano, sem o uso de fórmulas, e utilizar esse conhecimento para calcular, por exemplo, medidas de perímetros e áreas de figuras planas construídas no plano.
Objetivos específicos
Calcular o ponto médio em um segmento de reta no plano cartesiano.
Conceito-chave
Ponto médio de um segmento.
Recursos necessários
Malha quadriculada, lápis e régua.
Habilidades BNCC:
Objetivos de aprendizagem
Calcular o ponto médio em um segmento de reta no plano cartesiano.
Precisa de ajuda para criar uma aula personalizada?
Crie seu plano de aula em menos de um minuto no WhatsApp.
Aula
Resumo da aula
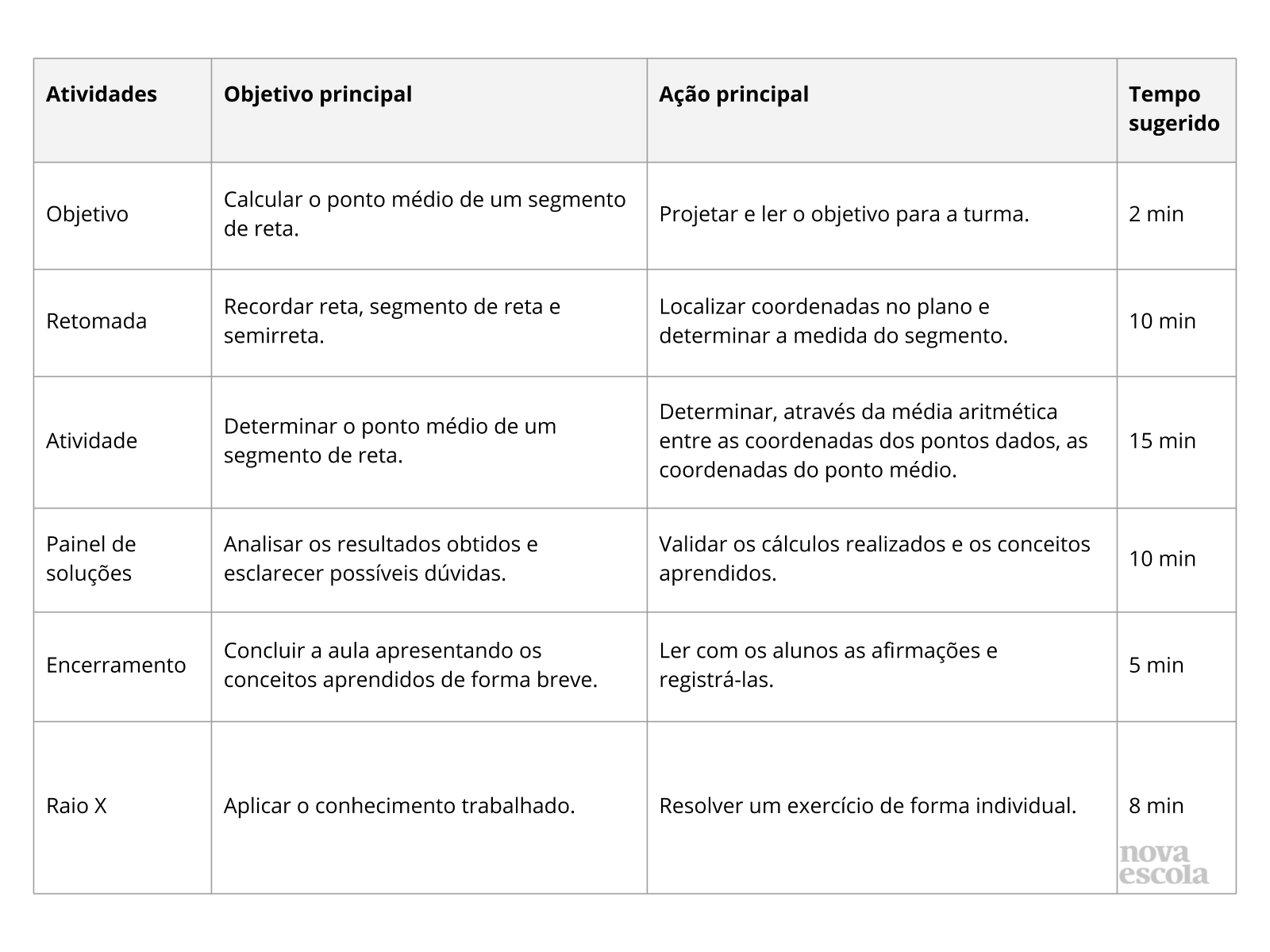Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo
Tempo sugerido: 2 minutos.
Orientações: Professor, leia com os alunos o objetivo da aula e garanta que saibam o significado dos termos matemáticos presentes.
Propósito: Apresentar o objetivo da aula.
Discuta com a Turma:
- O que é um ponto?
- O que é um segmento de reta?
Novo curso gratuito
Conheça nosso mais novo curso sobre adolescências, neurociência e engajamento nos anos finais
VER CURSO
