Guia de intervenções
Plano de Aula
Plano de aula: Receita matemática! Contando faces, vértices e arestas
Plano 6 de uma sequência de 10 planos. Veja todos os planos sobre Sólidos geométricos
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Poliana Aparecida Meredik Capelesso
Mentor: Daniela Pannuti
Revisor Pedagógico: Eliane Zanin
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
(EF02MA14) Reconhecimento e analisar figuras não planas, suas características e representações (esfera, cilindro, cubo, pirâmides, bloco retangular, prisma de base triangular, faces, arestas e vértices, planificação).
Objetivos específicos
Identificar e contar faces, vértices e arestas dos sólidos geométricos.
Conceito-chave
Reconhecer, classificar e diferenciar as figuras geométricas espaciais de acordo com algumas características, mais especificamente faces, vértices e arestas.
Recursos necessários
- Massinha de modelar/gomas,
- Palito de churrasco/dente ou picolé,
- Lápis,
- Borracha,
- Embalagens que representem os sólidos geométricos ou os próprios sólidos geométricos em madeira,
- Folha das Atividades (impressas, passadas no quadro);
- Datashow (opcional).
Habilidades BNCC:
Objetivos de aprendizagem
Identificar e contar faces, vértices e arestas dos sólidos geométricos.
Resumo da aula
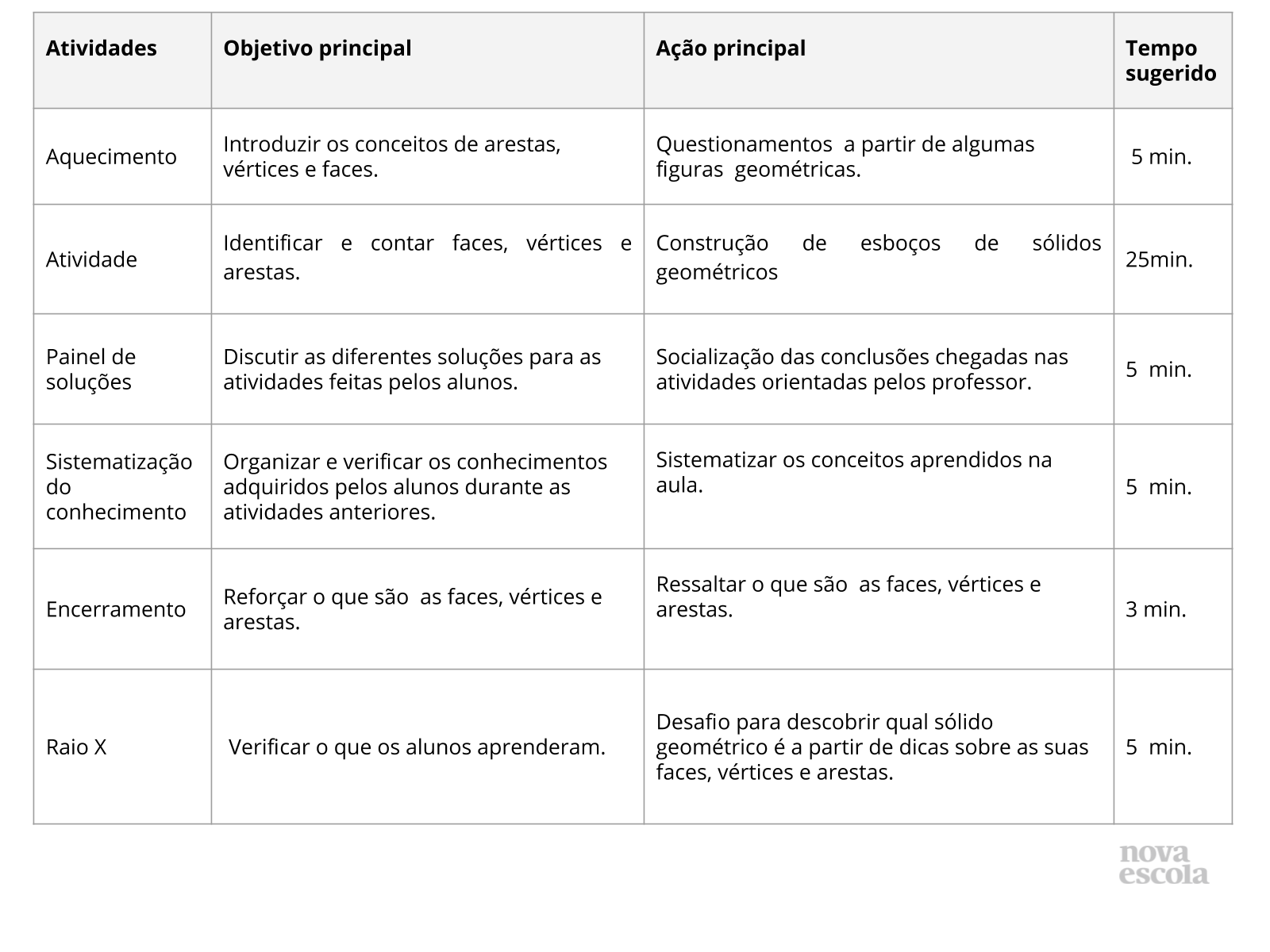 Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Leia o objetivo da aula para os alunos.
Propósito: Compartilhar o objetivo da aula com a turma.
Aquecimento

Tempo sugerido: 5 minutos.
Orientação: Providencie figuras geométricas não planas ou objetos que se assemelham a elas. Para esta aula sugere-se que sejam o cubo, paralelepípedo e pirâmide de base quadrangular. Discuta com turma. Ouça as respostas dos alunos. Pode ser que tenha algum aluno que já tenha algum conhecimento destes conceitos. Deixe que levantem hipóteses e depois fale que a hoje eles aprenderão a identificar aresta, vértice e face dos sólidos geométricos. Explique rapidamente que um vértice é o ponto comum entre os lados de uma figura geométrica, uma aresta é um segmento de reta onde duas faces se encontram e que face é cada um dos lados do sólido.
Propósito: Introduzir os conceitos de aresta, vértice e face.
Discuta com a turma:
- O que vocês acham que é uma aresta? Face? Vértice?
- Alguém poderia vir e me mostrar nestas figuras geométricas não planas onde fica a aresta, vértice ou face?
Organização a atividade principal

Tempo sugerido: 25 minutos.(slides 4 a 6)
Orientação: Organize da maneira que achar mais interessante os materiais a serem utilizados. Pode ser massinha de modelar/gomas e palitos de churrasco/dente/picolé. Sugere-se que a atividade seja feita em duplas, a fim que haja uma troca de experiências entre os alunos. Entregue os materiais para as duplas, o suficiente para montar um esboço de uma figura geométrica não plana. Por exemplo para a montagem de um cubo recomenda-se que cada aluno tenha no mínimo 12 palitos. Oriente os alunos para organizarem suas mesas para que não haja nenhum objeto que possa vir a atrapalhar na atividade e que não mexam nos materiais antes da explicação do que será feito.
Propósito: Organizar as duplas de trabalho e entregar os materiais necessários para a atividade.
Discuta com a turma:
- Todos receberam o materiais necessários para a atividade?
Materiais complementares:
Resolução da Atividade Principal
Material de Apoio:
As trocas que fazem a turma avançar
Atividade principal

Tempo sugerido: 25 minutos.(slides 4 a 6)
Orientação: Antes de iniciar a atividade com os alunos faça um modelo coletivo para exemplificar o que deve ser feito. Use o manual que está nos Materiais Complementares para verificar como deve ser feita a montagem das figuras geométricas não planas. Após deixe os alunos produzirem e explorar a suas produções. Nesta atividade você promoverá a autonomia dos alunos, seja um mediador da aprendizagem, observe a produção deles, apenas interfira quando achar necessário. Fica a critério a seu critério quantas figuras montar na atividade, sugere-se que sejam duas, ou no máximo três, e que todos sigam uma ordem e façam a mesma figura, com a finalidade de explorar coletivamente cada uma.Explique que depois de produzirem seus sólidos, eles farão a atividade para identificação de suas faces, arestas e vértices. Imprima a atividade para cada um dos alunos, você encontra nos Materiais Complementares. Se optar por fazer outros sólidos que não sejam os sugeridos, inclua-os ou substitua-os na atividade escrita. Diga que depois de tudo pronto, farão a socialização das produções e a correção da atividade.Circule entre eles e vá fazendo questionamentos individuais sobre os conceitos.
Propósito: Fazer com que os alunos compreendam a localização das faces, vértices e arestas.
Discuta com a turma:
- O cubo (ou outra figura geométrica) possui quantos vértices? Faces? E arestas?
- As arestas são sempre formadas pela junção de que? E os vértices?
- Alguém saberia me dizer o que concluiu sobre a face?
Sugere-se que a cada forma geométrica construída sejam feitos questionamentos.
Atividade principal
Tempo sugerido: 25 minutos. (slides 4 a 6)
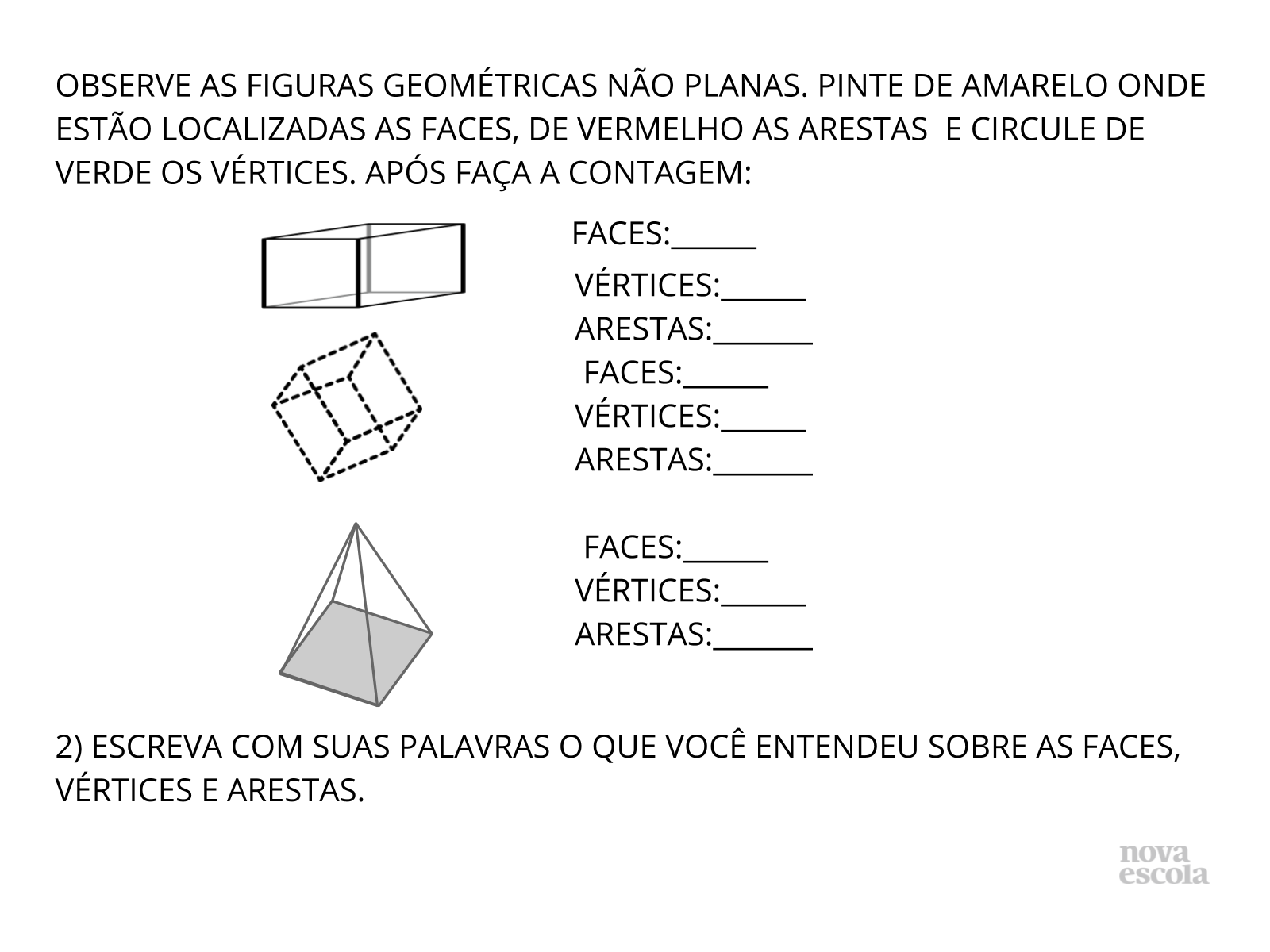
Orientação: Entregue uma cópia desta atividade para cada um dos alunos,você encontra nos Materiais Complementares. Explique que depois de produzirem seus sólidos, eles farão a atividade para identificação de suas faces, arestas e vértices. Se optar por fazer outros sólidos que não sejam os sugeridos, inclua-os ou substitua-os na atividade escrita. Diga que depois de tudo pronto, farão a socialização das produções e a correção da atividade.Circule entre eles e vá fazendo questionamentos individuais sobre os conceitos.Deixe que usem os sólidos produzidos para a identificação e contagem das faces, arestas e vértices. Ao final, peça que escrevam com suas palavras o que entenderam sobre as faces, vértices e arestas.
Propósito: Fazer com que os alunos identifiquem, conceituem e localizem as faces, vértices e arestas.
Discuta com a turma:
- O cubo (ou outra figura geométrica) possui quantos vértices? Faces? E arestas?
- As arestas são sempre formadas pela junção de que? E os vértices?
- Alguém saberia me dizer o que concluiu sobre a face?
Discussão das soluções

Tempo sugerido: 5 minutos.(slides 7 e 8)
Orientação: Estimule os alunos a compartilharem as suas produções. Após finalizar a aula, se possível, promova uma exposição das peças no pátio da escola, ou na própria sala. Faça com que os alunos verbalizem a nomenclatura do seu sólido produzido, bem como, peça para alguns alunos a identificarem as faces, vértices e arestas da figura.
Propósito: Socializar as produções e verbalizar os conceitos.
Discuta com a turma:
- Qual sólido geométrico você produziu?
- Aponte onde estão as faces. E as arestas? E os vértices, quantos são?
Discussão das soluções
Tempo sugerido: 5 minutos.(slides 7 e 8)
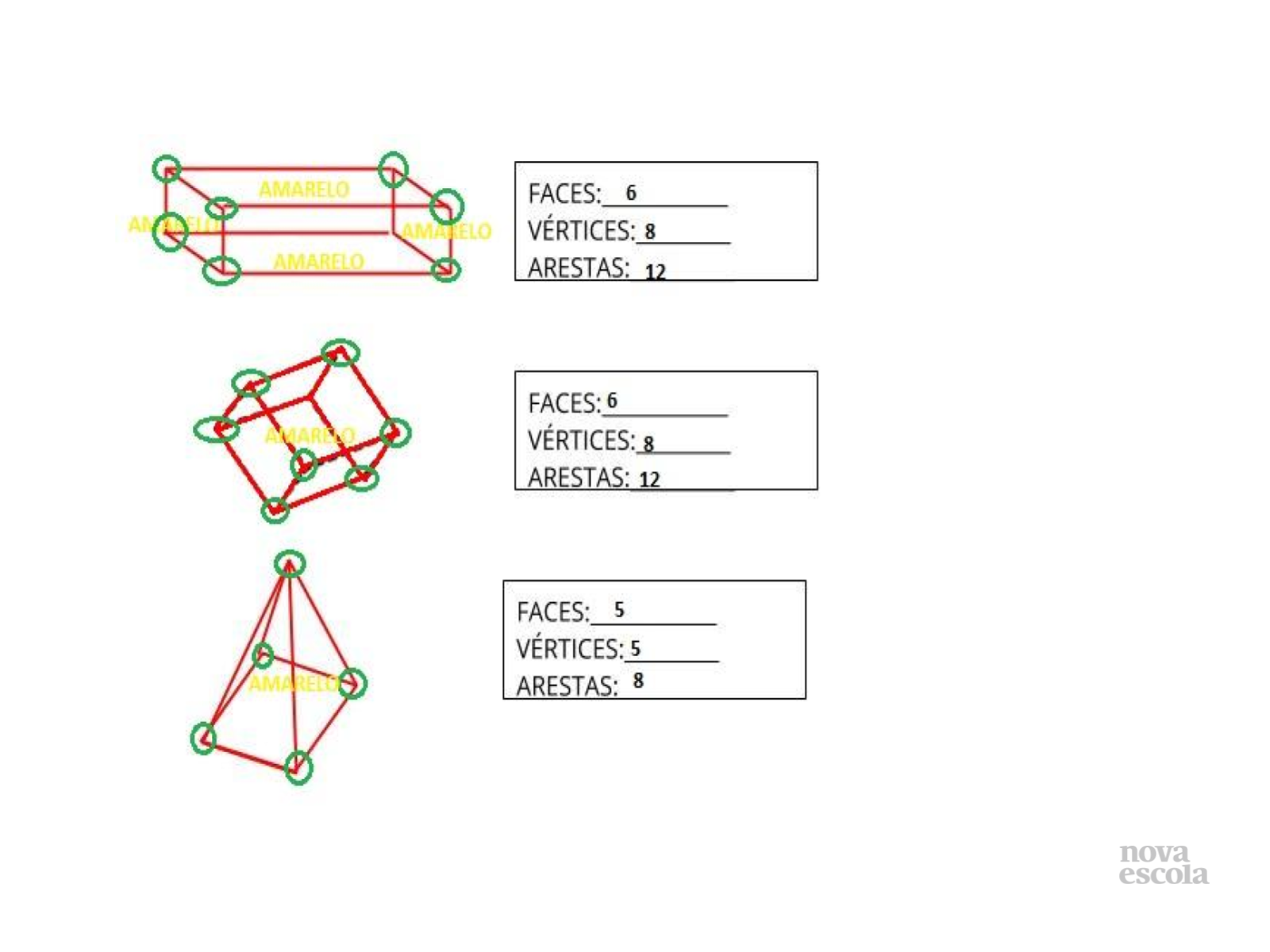
Orientação: Corrija a atividade escrita, coletivamente. Faça com que os alunos verbalizem as nomenclaturas dos sólidos produzidos pela turma, e digam quantas faces, vértices e arestas eles têm. Peça que falem com suas palavras o que entenderam sobre as faces, vértices e arestas.
Propósito: Discutir as soluções da atividade atividade principal a partir da troca de experiências entre os alunos.
Discuta com a turma:
- Como chamamos estes sólidos geométricos?
- Aponte onde estão as faces. E as arestas? E os vértices, quantos são?
- Quem poderia dizer a sua conclusão sobre o que são faces, vértice e arestas?
Sistematização do Conceito
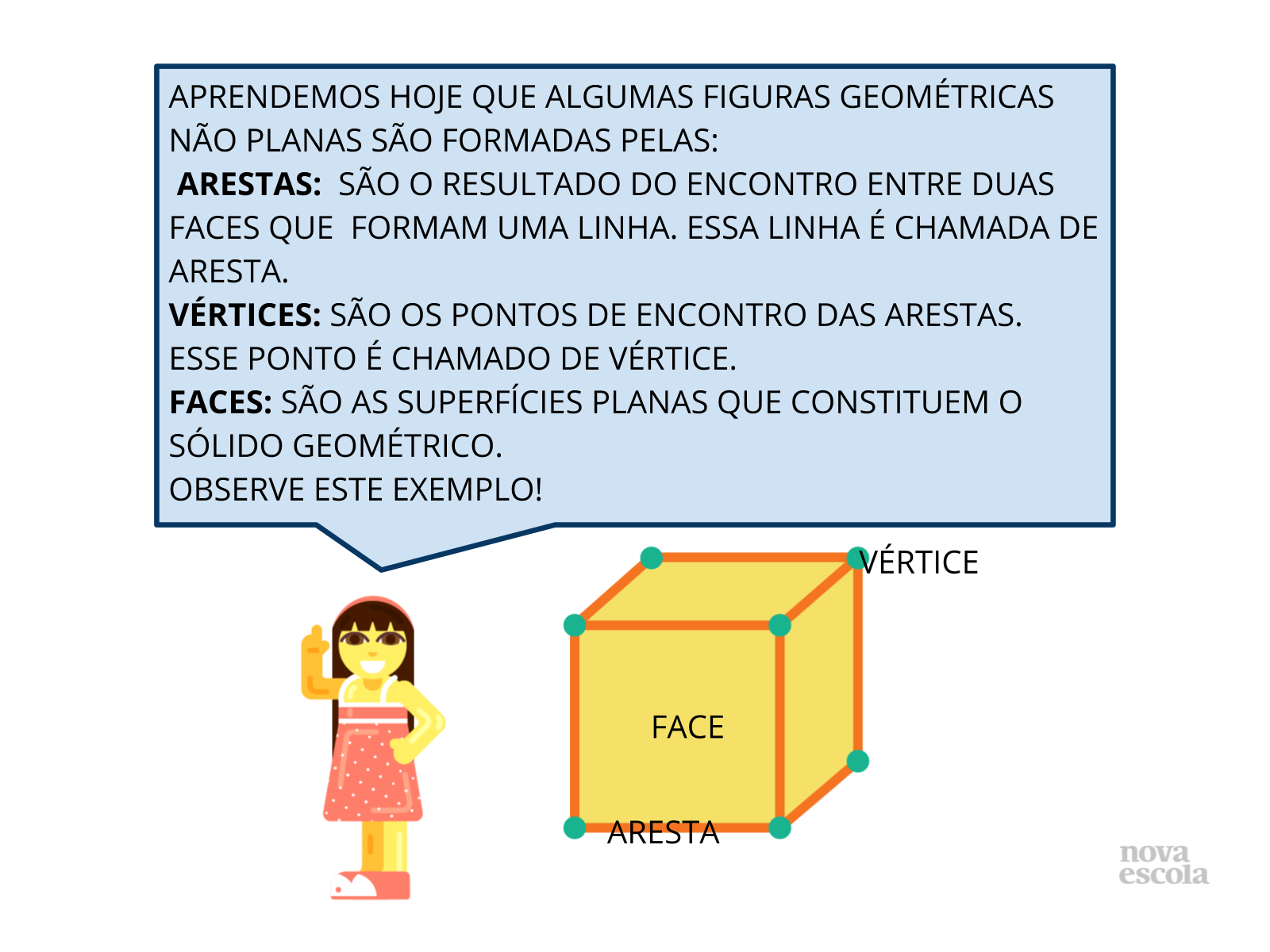
Tempo sugerido: 5 minutos.
Orientação: Retome a atividade realizada reforçando o que são faces, vértices e arestas. Procure fazer o desenho acima no quadro, ou projete este slide, a fim dos alunos visualizarem melhor cada uma das partes.
Propósito: Reforçar os conhecimentos obtidos nesta aula.
Encerramento
Tempo sugerido: 3 minutos.
Orientação: Projete este slide ou escreva o resumo no quadro e peça que registrem em seus cadernos.
Propósito: Resumir a aprendizagem do dia.
Raio X
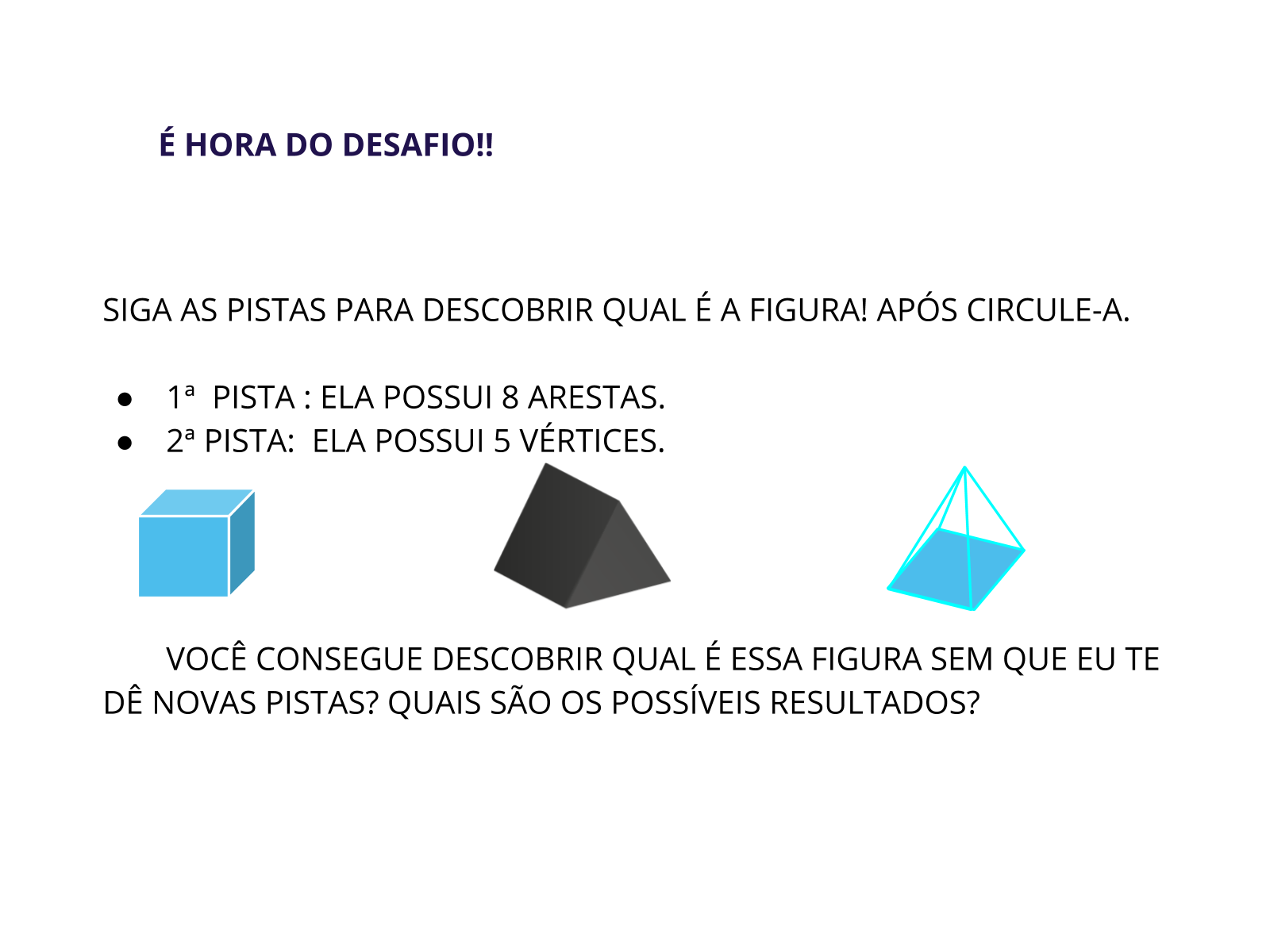
Tempo sugerido: 5 minutos.(slides 11 e 12)
Orientação: Realize a leitura do enunciado e peça aos alunos para que acompanhem esta leitura. Deixe com que os alunos resolvam a proposta individualmente. Enquanto produzem individualmente passe nas mesas para verificar o que eles estão conseguindo fazer ou não.
Discuta com a turma:
- Você consegue descobrir qual é essa figura sem que eu te dê novas pistas? Quais são os possíveis resultados?
- Por que você pensou nisso? Como você chegou neste resultado? ...).
- Existe só uma possibilidade de resposta?
Materiais complementares:
Raio X
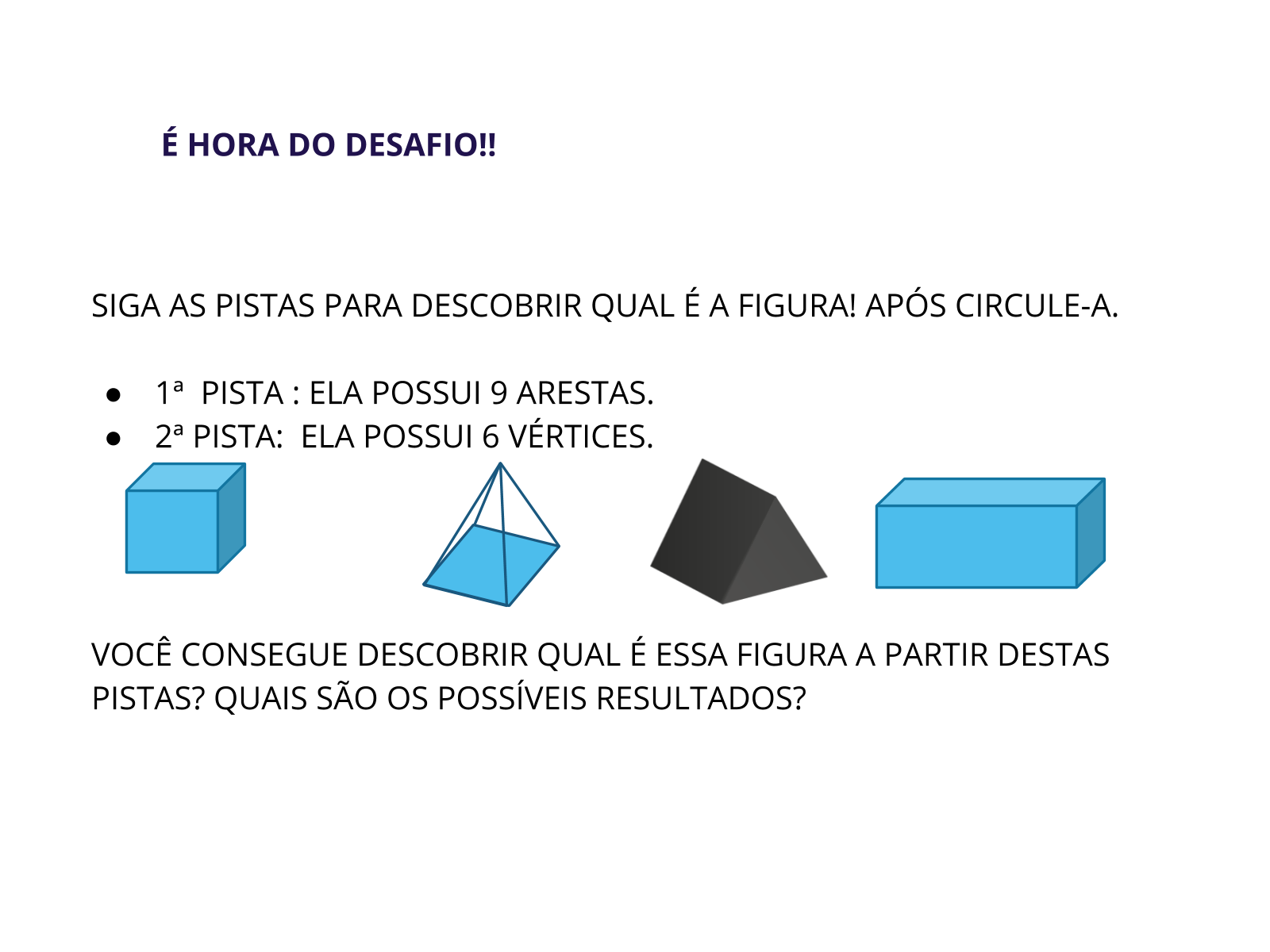
Tempo sugerido: 5 minutos..(slides 11 e 12)
Orientação: Realize a leitura do enunciado e peça aos alunos para que acompanhem esta leitura. Deixe com que os alunos resolvam a proposta individualmente. Enquanto produzem individualmente passe nas mesas para verificar o que eles estão conseguindo fazer ou não.
Discuta com a turma:
- Você consegue descobrir qual é essa figura sem que eu te dê novas pistas? Quais são os possíveis resultados?
- Por que você pensou nisso? Como você chegou neste resultado? ...).
- Existe só uma possibilidade de resposta?
Sugestão de adaptação para ensino remoto
Código do plano
MAT3_16GEO06
Recursos
- Necessários: estojo, papel ou caderno do aluno para que faça as anotações pertinentes.
Algum meio de comunicação com alunos: Zoom, Meet, Google sala de aula, WhatsApp, e-mail ou impressão (essa deve ser a última opção nesse momento de pandemia).
Atividade principal
Sólidos geométricos ou caixas, embalagens que lembrem sólidos geométricos.
Massinha de modelar/gomas/ miolo de pão,
Palito de churrasco/dente ou picolé, canudos, canudos feitos com páginas de jornal ou revistas.
- Opcionais:
Celular, computador ou tablet
Jogo: Sólidos geométricos
Jogo: Sólidos geométricos: Classificação.
Álbum virtual
Flipgrid
Para este plano, foque na etapa da Atividade principal
Aquecimento
O foco do plano deve ser a atividade principal, entretanto, vale a pena iniciar com a atividade de aquecimento para verificar os conhecimentos dos alunos sobre faces, vértices e arestas. Essa atividade pode ser enviada como forma de desafio antes da aula que será realizada. Envie a imagem do slide de aquecimento por WhatsApp ou e-mail e desafie os alunos a enviar suas respostas pelo mesmo meio. Através da atividade você poderá identificar o nível de compreensão da turma sobre esses conceitos.
Atividade principal
O foco desta atividade principal é identificar e contar faces, vértices e arestas dos sólidos geométricos. Os alunos devem ter em mãos: palitos (que podem ser de churrasco/dente ou picolé), canudos, canudos feitos com páginas de jornal ou revistas e massinha (gomas tipo jujuba ou até mesmo miolo de pão). Essa atividade pode ser realizada tanto de forma síncrona como assíncrona, por videoconferência ou por WhatsApp. Os alunos devem montar sólidos geométricos utilizando esses materiais. Cada aluno pode montar um sólido, não precisa montar todos. As instruções podem ser dadas ao vivo ou através de vídeo gravado modelando a atividade. A tabela para preenchimento pode ser enviada em forma de arquivo por e-mail ou WhatsApp. Peça que, se for possível, os alunos gravem um vídeo mostrando as suas produções e explicando como ela foi realizada e o que concluíram sobre os vértices, arestas e faces do sólido que construíram. Você pode pedir que disponibilizem no Flipgrid para que todos sejam disponibilizados para as famílias assistirem. Caso não seja possível, os alunos podem fotografar as suas produções e compartilhá-las em um álbum virtual. Cada um pode criar a legenda para sua produção explicando como foi realizada e suas conclusões.
Discussão das soluções
Na discussão das soluções os alunos devem compartilhar suas produções. Eles podem compartilhar via fotografia e texto ou áudio, ou mesmo gravar um vídeo mostrando sua produção e conclusões.
Você pode incentivar as discussões com perguntas para que possam efetuar comparações entre esses sólidos e suas planificações:
- Qual sólido geométrico você produziu?
- Aponte onde estão as faces. E as arestas? E os vértices, quantos são?
Sistematização do conceito e encerramento
Retome resumidamente com a turma os conceitos explorados na aula. Os alunos devem copiar em seus cadernos para futuras consultas. Pergunte se eles gostariam de acrescentar alguma observação às anotações.
Raio X
A atividade do Raio X pode ser utilizada para verificar se os alunos compreenderam e atingiram o objetivo da aula. As atividades complementares também podem ser exploradas para esse fim. Você pode selecionar as atividades que são mais adequadas para a sua turma e enviá-las pelo meio que está sendo usado por sua escola para interagir com os alunos.
Convite às famílias
Envie para as famílias uma mensagem de texto, áudio ou vídeo explicando o que você está trabalhando com os alunos e de que forma eles podem ajudar na organização ou discussão da resolução ou incentivar em casa.
O envolvimento das famílias nas atividades escolares com os alunos é o ideal nesses momentos, principalmente na organização da rotina deles e de seus materiais.
Esta é uma atividade divertida para ser realizada em família. Os familiares podem ajudar também na parte de gravar o vídeo ou fotografar as produções dos alunos. Pode também incentivar que os alunos joguem os jogos indicados, se for possível.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Poliana Aparecida Meredik Capelesso
Mentor: Daniela Pannuti
Revisor Pedagógico: Eliane Zanin
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
(EF02MA14) Reconhecimento e analisar figuras não planas, suas características e representações (esfera, cilindro, cubo, pirâmides, bloco retangular, prisma de base triangular, faces, arestas e vértices, planificação).
Objetivos específicos
Identificar e contar faces, vértices e arestas dos sólidos geométricos.
Conceito-chave
Reconhecer, classificar e diferenciar as figuras geométricas espaciais de acordo com algumas características, mais especificamente faces, vértices e arestas.
Recursos necessários
- Massinha de modelar/gomas,
- Palito de churrasco/dente ou picolé,
- Lápis,
- Borracha,
- Embalagens que representem os sólidos geométricos ou os próprios sólidos geométricos em madeira,
- Folha das Atividades (impressas, passadas no quadro);
- Datashow (opcional).