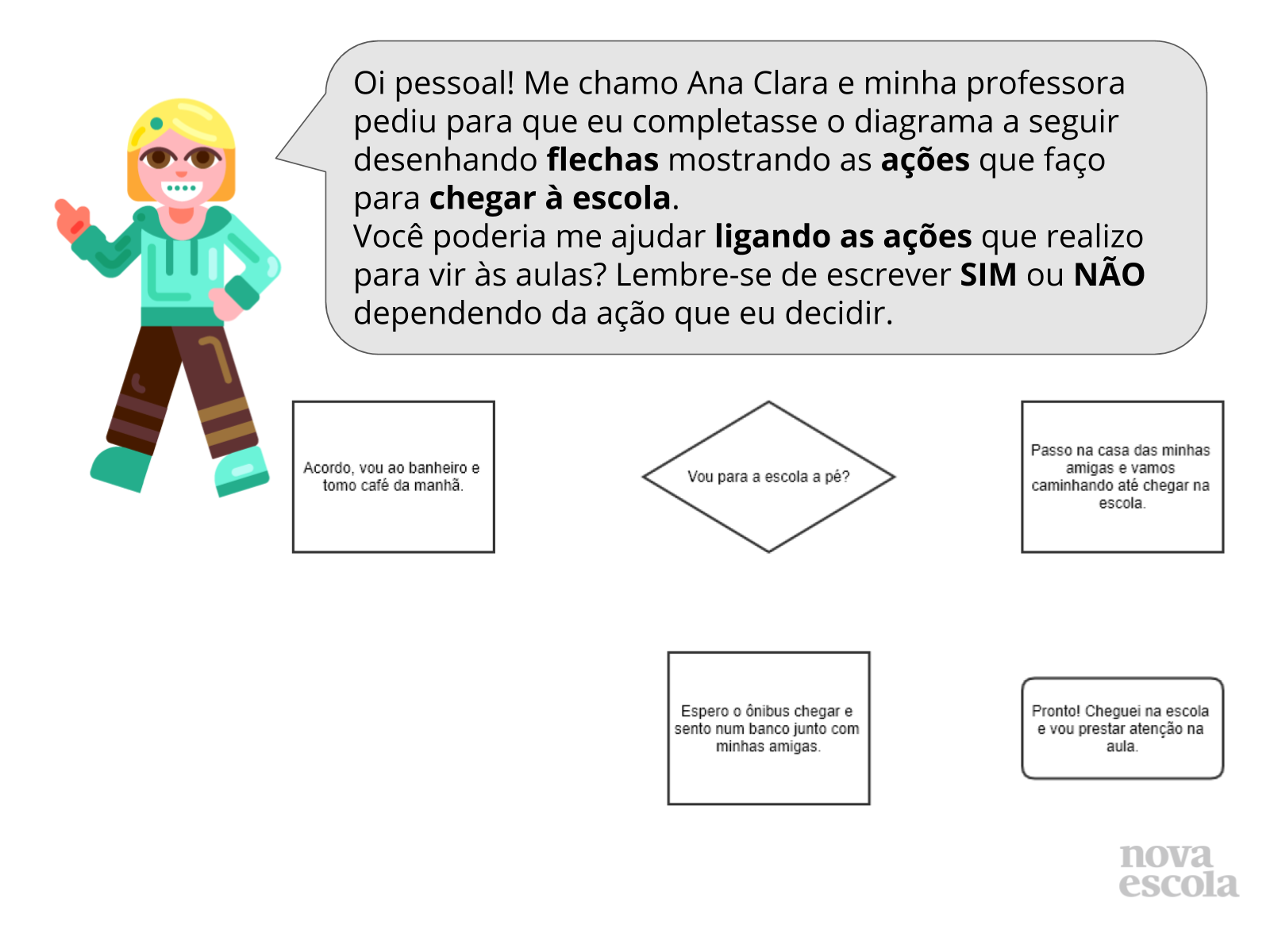
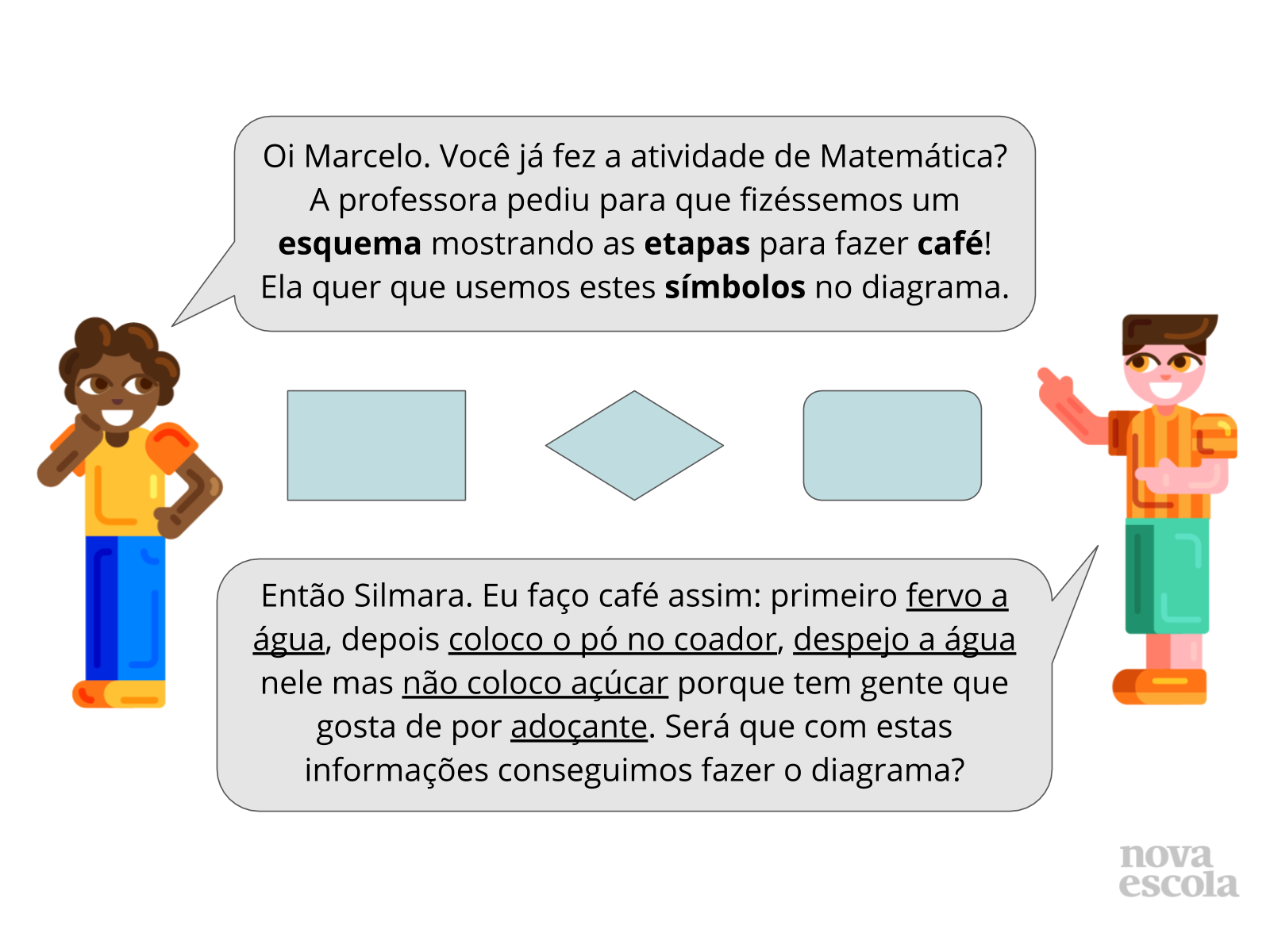
Resolução das atividades
Plano de Aula
Plano de aula: Uma receita para um polígono regular
Plano 4 de uma sequência de 5 planos. Veja todos os planos sobre Fluxogramas para a construção de polígonos
Tem interesse no tema "Neurociência, adolescências e engajamento nos Anos Finais"?
Inscreva-se neste tema para receber novidades pelo site e por email.
Descrição
MAT9_27GEO04 / Uma receita para um polígono regular
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Fabricio Eduardo Ferreira
Mentor: Rodrigo Morozetti Blanco
Habilidade da BNCC
(EF09MA14) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.
Objetivos específicos
- Desenhar com auxílio de régua e transferidor ângulos com medidas pré-definidas;
- Decompor polígonos em triângulos a partir de um único vértice;
- Calcular a soma dos ângulos internos de um polígono;
- Construir um polígono regular a partir da medida de um de seus ângulos internos com auxílio de régua e compasso;
- Descrever por escrito os passos para obtenção de um polígono regular.
Habilidades BNCC:
Objetivos de aprendizagem
- Desenhar com auxílio de régua e transferidor ângulos com medidas pré-definidas;
- Decompor polígonos em triângulos a partir de um único vértice;
- Calcular a soma dos ângulos internos de um polígono;
- Construir um polígono regular a partir da medida de um de seus ângulos internos com auxílio de régua e compasso;
- Descrever por escrito os passos para obtenção de um polígono regular.
Planeje suas aulas pelo whatsapp
Qualidade com economia de tempo
Aula
Resumo da aula
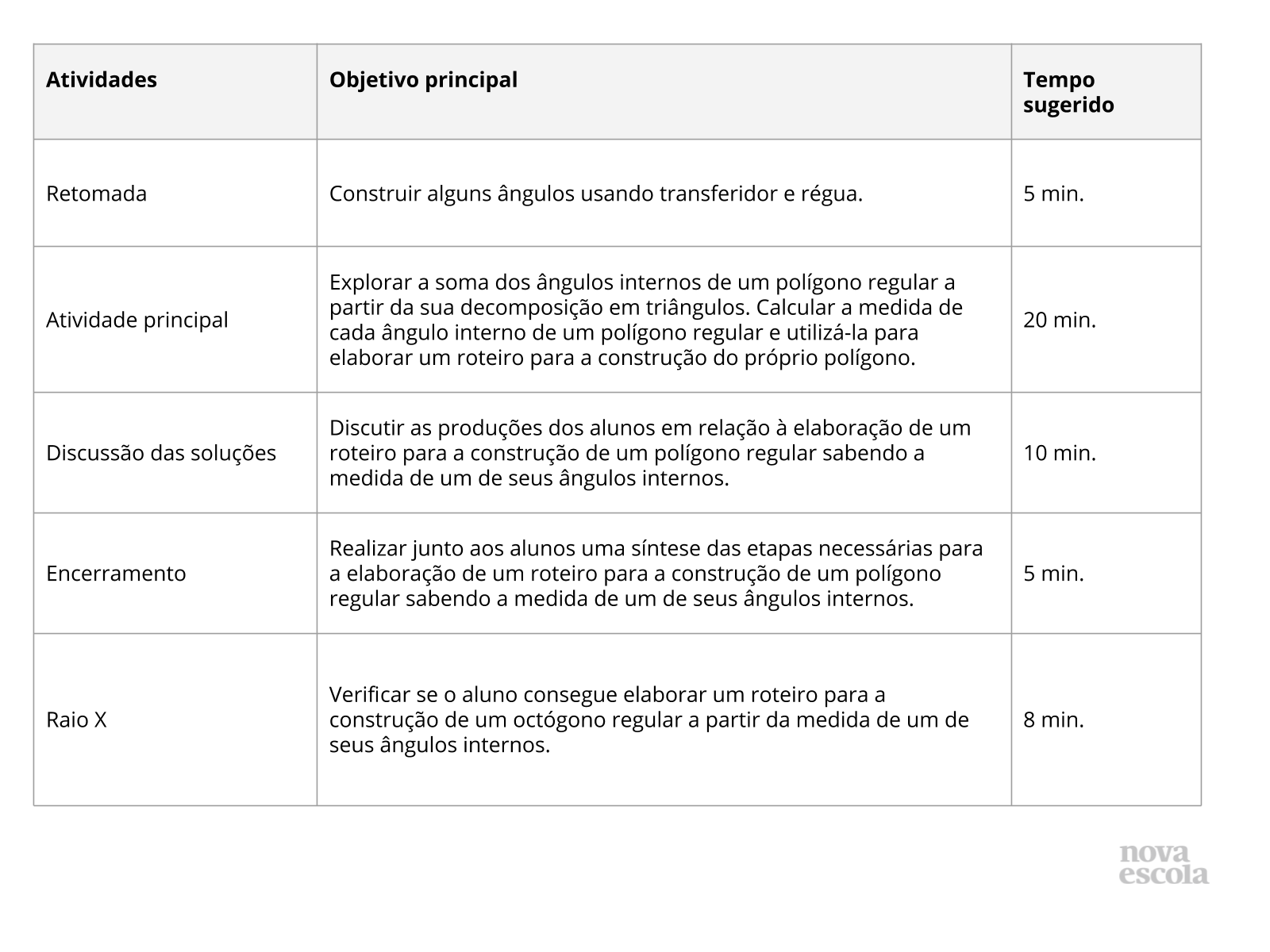
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão. O tempo sugerido prevê 48 minutos de atividade e 2 minutos para compartilhar com a turma o objetivo da aula.
Objetivo

Tempo sugerido: 2 minutos
Orientações:
Compartilhe com a turma o objetivo da aula lendo-o em voz alta, projetando-o (se estiver fazendo uso de apresentação de slides) ou escrevendo-o no quadro.
Novo curso gratuito

Conheça nosso mais novo curso sobre adolescências, neurociência e engajamento nos anos finais
VER CURSO