Atividade Principal
Plano de Aula
Plano de aula: Ladrilhando com polígonos regulares
Plano 9 de uma sequência de 10 planos. Veja todos os planos sobre Figuras bidimensionais: elementos e relações
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA.
Autora: Olenêva Sanches Sousa
Mentora: Paula Massi Reis Pires
Revisora Pedagógica: Eliane Zanin
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
EF5MA17: Reconhecer, nomear e comparar polígonos, considerando lados, vértices e ângulos, e desenhá-los, utilizando material de desenho ou tecnologias digitais.
Objetivos específicos
- Retomar o conceito de polígonos, na perspectiva de composições de mosaicos regulares;
- Fazer composições com polígonos regulares para formar mosaicos regulares;
- Discutir, coletivamente, sobre polígonos regulares e suas possibilidades de formação de mosaicos regulares;
- Pontuar características dos mosaicos regulares;
- Compor mosaicos regulares, reconhecendo os polígonos que os compõem.
Conceito-chave
Mosaicos regulares.
Recursos necessários
- Quadro e pincel;
- Computador;
- Projetor;
- GeoGebra;
- Impressora;
- Internet;
- Atividades impressas da atividade principal - 3º momento (uma cópia para cada trio);
- Atividade raio x (uma cópia por estudante);
- Apresentação dos 5 slides da Atividade Principal (para ser colocada nos computadores de uso discente e para serem projetadas quando em trabalhos coletivos, como nos momentos 1, especialmente, e 2);
- Cronômetro.
Habilidades BNCC:
Objetivos de aprendizagem
- Retomar o conceito de polígonos, na perspectiva de composições de mosaicos regulares;
- Fazer composições com polígonos regulares para formar mosaicos regulares;
- Discutir, coletivamente, sobre polígonos regulares e suas possibilidades de formação de mosaicos regulares;
- Pontuar características dos mosaicos regulares;
- Compor mosaicos regulares, reconhecendo os polígonos que os compõem.
Resumo da aula
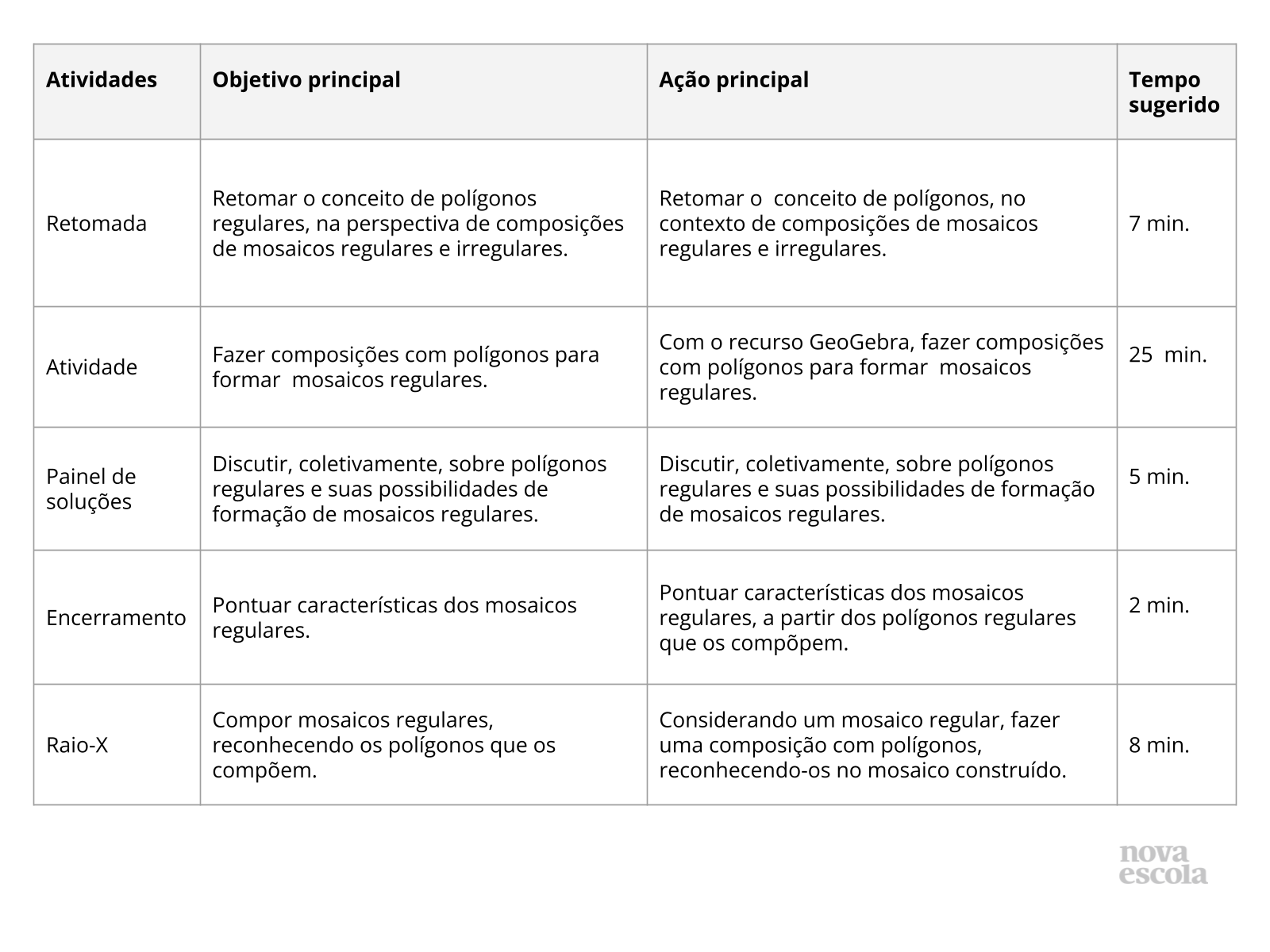
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar a proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo
Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo sugerido: 7 minutos (slides 3, 4 e 5).
Orientação:
- Utilize os slides 3, 4 e 5 como recurso às reflexões acerca das características de um mosaico regular e dos polígonos regulares que o compõem.
- Embora esta aula esteja prevista para ser realizada em um laboratório de informática ou com recursos individuais se necessário, use o quadro para complementações. Em síntese, busque fazer com que todos saibam (ou relembrem) o que é uma composição de polígonos.
- Estando em um laboratório de informática, faça uma apresentação dos slides desta aula, para que todos possam acompanhar em seus computadores, nos momentos que envolvem toda a turma e apenas os grupos.
- Apenas como sugestão, questione se os estudantes conhecem letra e música de “Se essa rua fosse minha” e, principalmente, o verbo ladrilhar. Se desejar, fale um pouco sobre essa música popular infantil, de domínio público e sugira que ouçam ou assistam algum vídeo com alguma versão da música. Também como sugestão, existe uma versão rock, com crianças de 5 a 8 anos, que você pode conhecer e, se quiser, indicar para a turma. Para assistir, no YouTube, clique aqui.
- Vá ao Discuta com a turma para ver intervenções, ponderando as mais relevantes ao seu contexto, no momento.
Propósito: Retomar o conceito de polígonos regulares e suas possibilidades de composição em um plano, formando mosaicos.
Discuta com a turma :
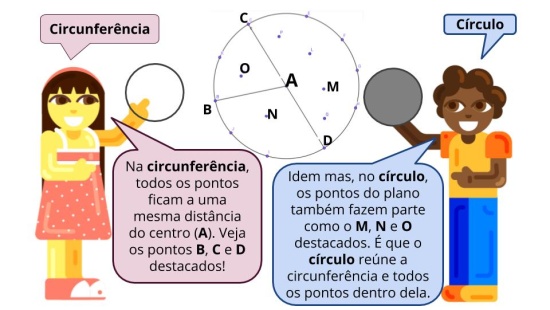
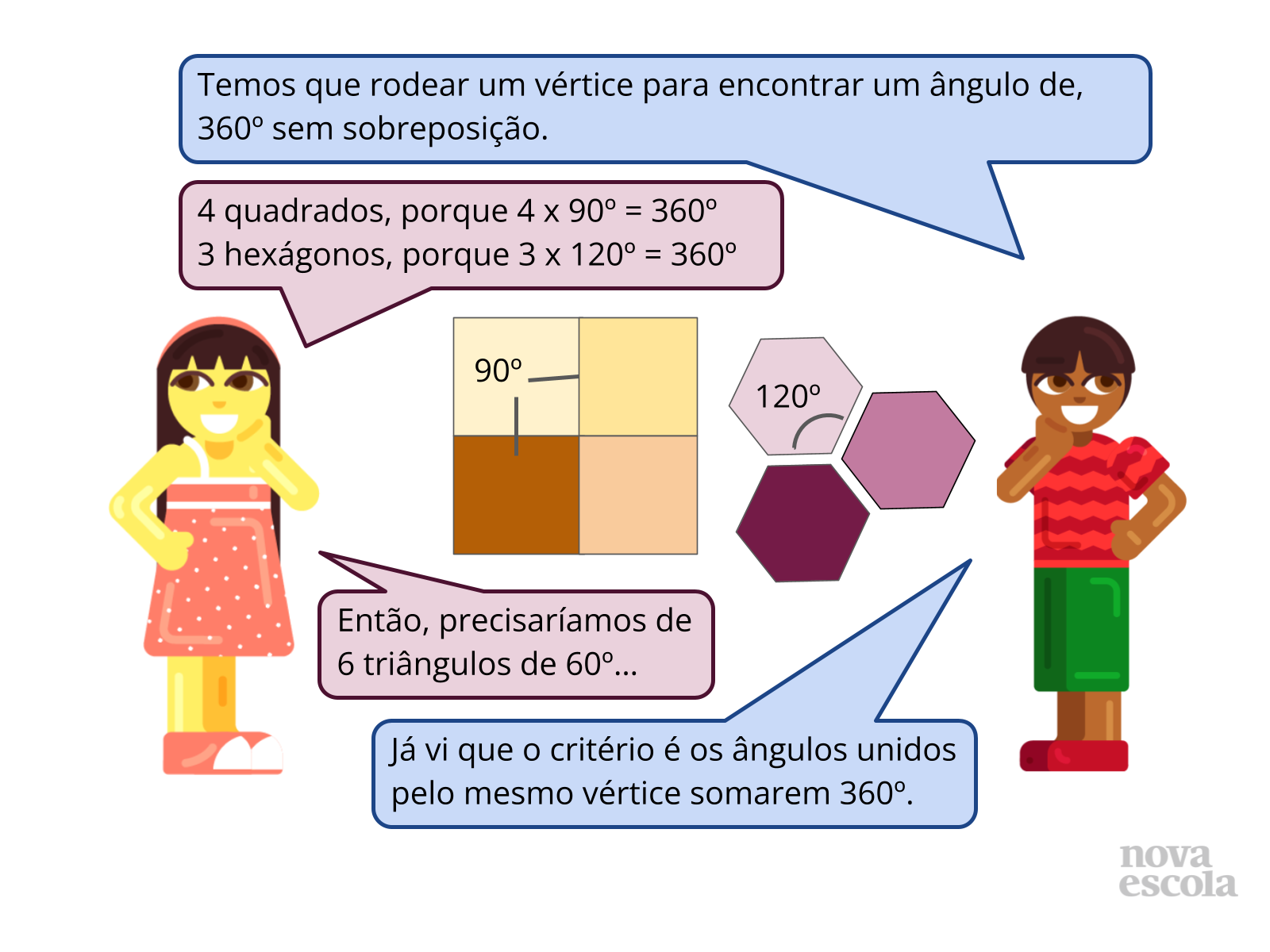
Slide 3 - Foco nos 360º que preenchem um plano: Peça para que os estudantes leiam, silenciosamente, o slide; use as “falas” para puxar a discussão:
- Pode me mostrar, com sua mão, o que a garota quis dizer com “cobrir os 360º”?
- Você pode definir, com suas palavras, o que é um mosaico?
- Para você, por que podemos formar mosaicos (360º) com polígonos? Poderíamos formar com círculos, por exemplo?
- Na ilustração com o mosaico quadrado, o que representa 90º?
- Quantos ângulos de 90º tem um quadrado? Por quê?
- Por que, ainda no mosaico quadrado, os 4 quadrados, lado a lado, unidos por um vértice comum, forma um mosaico?
- E no mosaico formado por 3 hexágonos, o que representa 120º?
- Por que precisamos de 4 quadrados no mosaico de quadrados para uni-los lado a lado por um vértice comum?
- Por que precisamos apenas de 3 figuras no mosaico de hexágonos regulares para uni-los lado a lado por um vértice comum?
- O quadrado e o hexágono, utilizados no exemplo deste slide, são polígonos regulares? Por quê?
Retomada
Tempo sugerido: 7 minutos (slides 3, 4 e 5).
Orientação:
- Utilize os slides 3, 4 e 5 como recurso às reflexões acerca das características de um mosaico regular e dos polígonos regulares que o compõem.
- Embora esta aula esteja prevista para ser realizada em um laboratório de informática ou com recursos individuais se necessário, use o quadro para complementações. Em síntese, busque fazer com que todos saibam (ou relembrem) o que é uma composição de polígonos.
- Estando em um laboratório de informática, faça uma apresentação dos slides desta aula, para que todos possam acompanhar em seus computadores, nos momentos que envolvem toda a turma e apenas os grupos.
- Apenas como sugestão, questione se os estudantes conhecem letra e música de “Se essa rua fosse minha” e, principalmente, o verbo ladrilhar. Se desejar, fale um pouco sobre essa música popular infantil, de domínio público e sugira que ouçam ou assistam algum vídeo com alguma versão da música. Também como sugestão, existe uma versão rock, com crianças de 5 a 8 anos, que você pode conhecer e, se quiser, indicar para a turma. Para assistir, no YouTube, clique aqui.
- Vá ao Discuta com a turma para ver intervenções, ponderando as mais relevantes ao seu contexto, no momento.
Propósito: Retomar o conceito de polígonos regulares e suas possibilidades de composição em um plano, formando mosaicos.
Discuta com a turma :
Slide 4 - Foco nos ângulos dos polígonos para formarem mosaicos: Peça para que os estudantes analisem o slide para puxar a discussão, a exemplo de:
- Pode me mostrar, nas figuras de mosaicos deste slide, qual a medida do ângulo que rodearia um ponto qualquer? Por que a soma das medidas dos ângulos internos dos polígonos, neste vértice, tem que dar 360º?
- Poderia me explicar os cálculos feitos pela garota? (Ela multiplicou o valor de um ângulo interno do polígono para ver se pode juntar esses ângulos em um único vértice para preencher um plano de 360º, se o produto da multiplicação der 360º, há o preenchimento. Desse modo, o multiplicador indica, portanto, quantos polígonos são utilizados no preenchimento).
- Por que a garota afirma que “precisamos de 6 triângulos de 60º”? (Porque 6 vezes 60º é igual a 360º).
- Você sabe quanto mede a soma dos ângulos internos de um triângulo? Existe triângulo com 3 ângulos de 60º? Como ele se chama?
Retomada
Tempo sugerido: 7 minutos (slides 3, 4 e 5).
Orientação:
- Utilize os slides 3, 4 e 5 como recurso às reflexões acerca das características de um mosaico regular e dos polígonos regulares que o compõem.
- Embora esta aula esteja prevista para ser realizada em um laboratório de informática ou com recursos individuais se necessário, use o quadro para complementações. Em síntese, busque fazer com que todos saibam (ou relembrem) o que é uma composição de polígonos.
- Estando em um laboratório de informática, faça uma apresentação dos slides desta aula, para que todos possam acompanhar em seus computadores, nos momentos que envolvem toda a turma e apenas os grupos.
- Apenas como sugestão, questione se os estudantes conhecem letra e música de “Se essa rua fosse minha” e, principalmente, o verbo ladrilhar. Se desejar, fale um pouco sobre essa música popular infantil, de domínio público e sugira que ouçam ou assistam algum vídeo com alguma versão da música. Também como sugestão, existe uma versão rock, com crianças de 5 a 8 anos, que você pode conhecer e, se quiser, indicar para a turma. Para assistir, no YouTube, clique aqui.
- Vá ao Discuta com a turma para ver intervenções, ponderando as mais relevantes ao seu contexto, no momento.
Propósito: Retomar o conceito de polígonos regulares e suas possibilidades de composição em um plano, formando mosaicos.
Discuta com a turma :
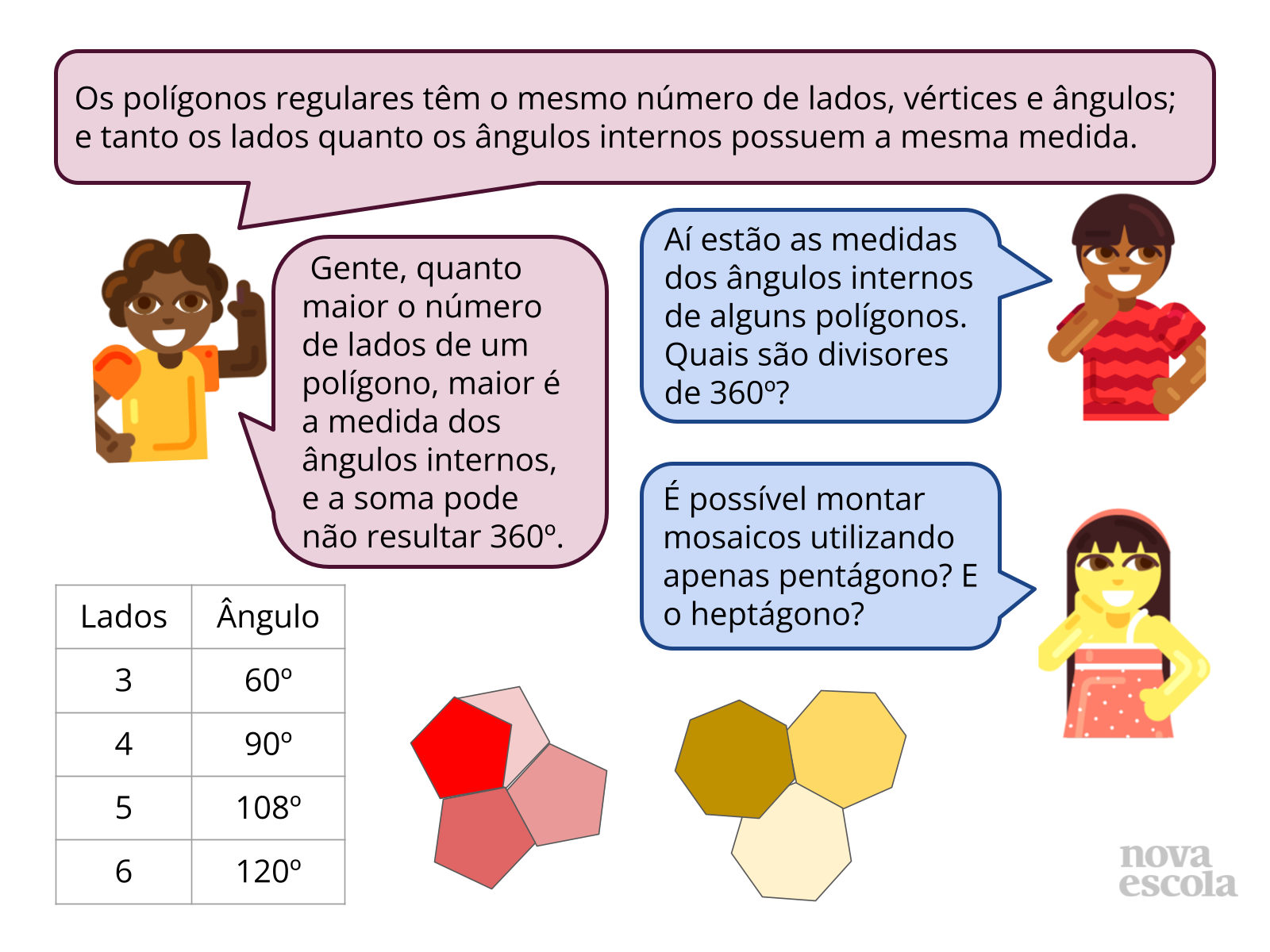
Slide 5 - Foco nos polígonos regulares que formam mosaicos regulares: Peça para que os estudantes analisem o slide para puxar a discussão:
- Você pode fazer um esboço de um polígono regular qualquer? Quais as características principais da figura para que ela seja classificada como regular?
- Na tabela de lados e ângulos de polígonos regulares, como se chama a figura que tem 3 lados? Quantos ângulos ela tem?
- Qual a medida desses ângulos? São todos iguais ou há diferenças? Você pode esboçar este triângulo regular e me mostrar esses ângulos? Como se chama este triângulo regular? Há triângulos não regulares? Quais? Por quê? Na mesma tabela, qual é a figura de 4 lados e com ângulos de 90º? Pode esboçá-la? Conhece outra figura de 4 lados e 4 ângulos de 90º m que não seja um polígono regular?
- Por que é importante observar “os ângulos dos polígonos que são divisores de 360º”, quando desejamos formar mosaicos?
- O pentágono regular tem que medida dos seus ângulos internos? (Conforme tabela, 108º) É divisor de 360º? Formaria um mosaico? Pode mostrar, com base no mosaico de pentágonos regulares do slide, o que acontece se quisermos formar um mosaico com eles?
- Pode mostrar, com base no mosaico de heptágonos regulares do slide, o que acontece se quisermos formar um mosaico com heptágonos?
- E se tentarmos com um octógono ou um decágono?
- Por que a garota achou que esses dados da tabela eram suficientes e não pesquisou mais valores de ângulos internos de polígonos regulares com maior número de lados?
- Você pode explicar a afirmação da garota de que “quanto maior o número de lados, maior é a medida dos ângulos internos”?
(É esperado que concluam que quanto maior o número de lados, maior é a abertura dos ângulos dos segmentos de reta que fecham o polígono).
Atividade Principal

Tempo sugerido: 25 minutos (slides 6, 7, 8, 9 e 10).
Orientações:
- Utilize o slide 6 para pontuar, brevemente, os 3 momentos da atividade, explicando que os dois primeiros serão cumpridos coletivamente, por toda a turma, e o terceiro, em trios, no GeoGebra.
- Esta aula considera que os estudantes já tiveram algum contato anterior com o GeoGebra, mas se não tiveram, sugerimos que oriente os estudantes, em aulas anteriores, que experimentem o aplicativo em casa e que ele dá 2 opções de uso, on line ou baixando no computador.
- Esta aula deve ser desenvolvida, preferencialmente, em um laboratório de informática, que comporte 3 estudantes por computador, e com um projetor; alternativamente, podem ser usados recursos tecnológicos individuais, com acesso à internet, mas é interessante o projetor, para que sejam realizados os 2 primeiros momentos, coletivamente, com todos da turma.
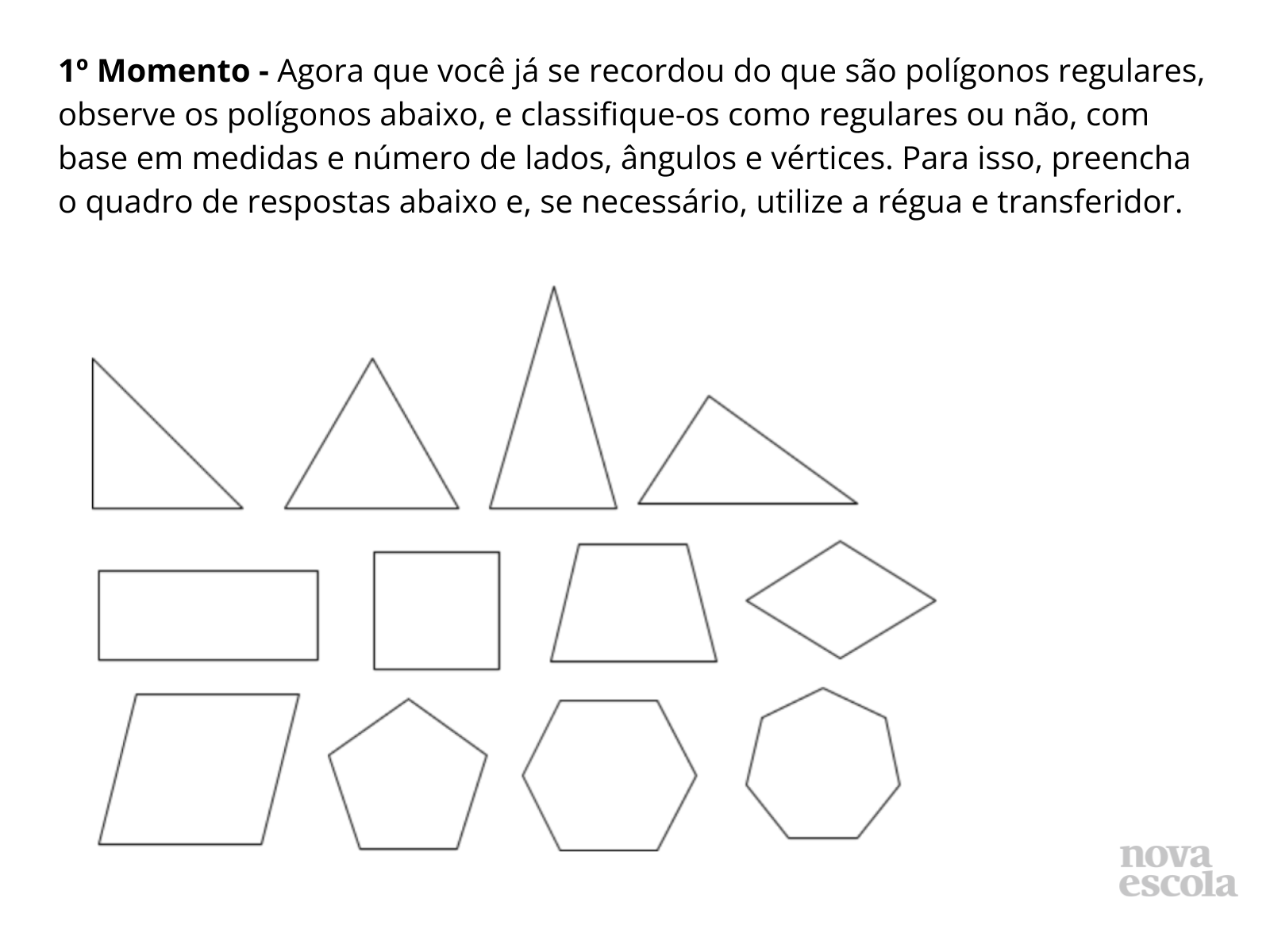
- Em seguida, vá para o slide 7, utilizando-o para apresentar a proposta do primeiro momento da atividade com toda a turma, de modo coletivo.
- Projete a apresentação do slide 7 para que todos acompanhem e participem; todos devem estar com o mesmo slide em seus computadores.
- Faça mediações para toda a turma, iniciando pela numeração dos polígonos e pela questão por que esses polígonos são regulares, com base em medidas e número de lados, ângulos e vértices, preenchendo o quadro de respostas, que será exibido no próximo slide.
- Em seguida, vá para o slide 8 e, com o quadro de resposta projetado, vá mediando o seu preenchimento e inserindo os dados solicitados.
- Confira, em Discuta com a Turma, abaixo, algumas questões provocativas para reflexões acerca do conteúdo em pauta, e as expectativas de respostas dos estudantes, entre parênteses, ponderando a relevância para o seu contexto, no momento.
- Não exceda mais de 5 minutos para esta etapa de análise dos polígonos, reconhecimento dos regulares e preenchimento do quadro-resposta.
- Utilize o slide 9 apenas para dizer que assistirão a um vídeo sobre as condições para os polígonos regulares formarem mosaico.
- Exiba o vídeo, com duração de 2:58 min, para todos e diga que os comentários serão feitos em seguida. Assista ao vídeo aqui.
- Confira, em Discuta com a Turma, abaixo, algumas questões provocativas para reflexões acerca do conteúdo do vídeo, ponderando a relevância.
- Não exceda mais de 3 minutos na discussão sobre o conteúdo do vídeo.
- Vá para o slide 10 e explique que trabalharão em trio e que farão mosaicos regulares.
- Observe se todos estão conectados à internet com o aplicativo GeoGebra.
- Explique que o objetivo da atividade é utilizar o GeoGebra para preencher com polígonos um determinado plano, cobrindo os seus 360º.
- Explique que devem seguir as orientações contidas na própria atividade, mas enfatize que, no GeoGebra, devem usar o ambiente Geometria.
- Observe que, na atividade, é sugerida a exibição de uma malha quadriculada para fazer o desenho, mas que esta escolha é opcional.
- Explique, também, que, a partir do desenho dos polígonos, os trios devem escolher Polígonos Regulares.
- Diga-lhes que estará presente para acompanhar o trabalho dos grupos.
- Explicite que a construção dos mosaicos não deve exceder 15 minutos.
- Imprima previamente a Atividade Principal.
- Considere as seguintes Atividades Complementares, para você ver mais possibilidades pedagógicas para o assunto mosaico com polígonos:
Atividades Complementares ao Professor:
1ª) Para saber mais sobre ladrilhos, sugerimos a leitura do artigo “Ladrilhamentos”, de Elvia Mureb Sallum, da Matemateca do Instituto de Matemática e Estatística da Universidade de São Paulo (IME-USP). Leia o artigo na íntegra, clicando aqui.
2ª) Para conhecer mais sobre mosaicos, leio o material “Mosaicos” do Laboratório de Ensino de Matemática da Universidade de Brasília (LEMAT-UnB), disponível aqui.
3ª) Material complementar do LEMAT-UnB de Solução das atividades com mosaicos”, disponível aqui.
- Lembre-se de que você dispõe de questões provocadoras, no Guia de Intervenção, que pode ser acessado aqui.
- Confira a Atividade Principal, acessando aqui.
Propósito: Fazer composições com polígonos para formar mosaicos regulares.
Materiais complementares:
Atividade Principal
Atividade Principal
Tempo sugerido: 25 minutos (slides 6, 7, 8, 9 e 10).
Orientações:
- Utilize o slide 6 para pontuar, brevemente, os 3 momentos da atividade, explicando que os dois primeiros serão cumpridos coletivamente, por toda a turma, e o terceiro, em trios, no GeoGebra.
- Esta aula considera que os estudantes já tiveram algum contato anterior com o GeoGebra, mas se não tiveram, sugerimos que oriente os estudantes, em aulas anteriores, que experimentem o aplicativo em casa e que ele dá 2 opções de uso, on line ou baixando no computador.
- Esta aula deve ser desenvolvida, preferencialmente, em um laboratório de informática, que comporte 3 estudantes por computador, e com um projetor; alternativamente, podem ser usados recursos tecnológicos individuais, com acesso à internet, mas é interessante o projetor, para que sejam realizados os 2 primeiros momentos, coletivamente, com todos da turma.
- Em seguida, vá para o slide 7, utilizando-o para apresentar a proposta do primeiro momento da atividade com toda a turma, de modo coletivo.
- Projete a apresentação do slide 7 para que todos acompanhem e participem; todos devem estar com o mesmo slide em seus computadores.
- Faça mediações para toda a turma, iniciando pela numeração dos polígonos e pela questão por que esses polígonos são regulares, com base em medidas e número de lados, ângulos e vértices, preenchendo o quadro de respostas, que será exibido no próximo slide.
- Em seguida, vá para o slide 8 e, com o quadro de resposta projetado, vá mediando o seu preenchimento e inserindo os dados solicitados.
- Confira, em Discuta com a Turma, abaixo, algumas questões provocativas para reflexões acerca do conteúdo em pauta, e as expectativas de respostas dos estudantes, entre parênteses, ponderando a relevância para o seu contexto, no momento.
- Não exceda mais de 5 minutos para esta etapa de análise dos polígonos, reconhecimento dos regulares e preenchimento do quadro-resposta.
- Utilize o slide 9 apenas para dizer que assistirão a um vídeo sobre as condições para os polígonos regulares formarem mosaico.
- Exiba o vídeo, com duração de 2:58 min, para todos e diga que os comentários serão feitos em seguida. Assista ao vídeo aqui.
- Confira, em Discuta com a Turma, abaixo, algumas questões provocativas para reflexões acerca do conteúdo do vídeo, ponderando a relevância.
- Não exceda mais de 3 minutos na discussão sobre o conteúdo do vídeo.
- Vá para o slide 10 e explique que trabalharão em trio e que farão mosaicos regulares.
- Observe se todos estão conectados à internet com o aplicativo GeoGebra.
- Explique que o objetivo da atividade é utilizar o GeoGebra para preencher com polígonos um determinado plano, cobrindo os seus 360º.
- Explique que devem seguir as orientações contidas na própria atividade, mas enfatize que, no GeoGebra, devem usar o ambiente Geometria.
- Observe que, na atividade, é sugerida a exibição de uma malha quadriculada para fazer o desenho, mas que esta escolha é opcional.
- Explique, também, que, a partir do desenho dos polígonos, os trios devem escolher Polígonos Regulares.
- Diga-lhes que estará presente para acompanhar o trabalho dos grupos.
- Explicite que a construção dos mosaicos não deve exceder 15 minutos.
- Imprima previamente a Atividade Principal.
- Considere as seguintes Atividades Complementares, para você ver mais possibilidades pedagógicas para o assunto mosaico com polígonos:
Atividades Complementares ao Professor:
1ª) Para saber mais sobre ladrilhos, sugerimos a leitura do artigo “Ladrilhamentos”, de Elvia Mureb Sallum, da Matemateca do Instituto de Matemática e Estatística da Universidade de São Paulo (IME-USP). Leia o artigo na íntegra, clicando aqui.
2ª) Para conhecer mais sobre mosaicos, leio o material “Mosaicos” do Laboratório de Ensino de Matemática da Universidade de Brasília (LEMAT-UnB), disponível aqui.
3ª) Material complementar do LEMAT-UnB de Solução das atividades com mosaicos”, disponível aqui.
- Lembre-se de que você dispõe de questões provocadoras, no Guia de Intervenção, que pode ser acessado aqui.
- Confira a Atividade Principal, acessando aqui.
Propósito: Fazer composições com polígonos para formar mosaicos regulares.
Discuta com a turma :
Slide 7:
- Que características deve ter um polígono regular?
- Quais os polígonos regulares apresentados? Por quê?
Atividade Principal
Tempo sugerido: 25 minutos (slides 6, 7, 8, 9 e 10).
Orientações:
- Utilize o slide 6 para pontuar, brevemente, os 3 momentos da atividade, explicando que os dois primeiros serão cumpridos coletivamente, por toda a turma, e o terceiro, em trios, no GeoGebra.
- Esta aula considera que os estudantes já tiveram algum contato anterior com o GeoGebra, mas se não tiveram, sugerimos que oriente os estudantes, em aulas anteriores, que experimentem o aplicativo em casa e que ele dá 2 opções de uso, on line ou baixando no computador.
- Esta aula deve ser desenvolvida, preferencialmente, em um laboratório de informática, que comporte 3 estudantes por computador, e com um projetor; alternativamente, podem ser usados recursos tecnológicos individuais, com acesso à internet, mas é interessante o projetor, para que sejam realizados os 2 primeiros momentos, coletivamente, com todos da turma.
- Em seguida, vá para o slide 7, utilizando-o para apresentar a proposta do primeiro momento da atividade com toda a turma, de modo coletivo.
- Projete a apresentação do slide 7 para que todos acompanhem e participem; todos devem estar com o mesmo slide em seus computadores.
- Faça mediações para toda a turma, iniciando pela numeração dos polígonos e pela questão por que esses polígonos são regulares, com base em medidas e número de lados, ângulos e vértices, preenchendo o quadro de respostas, que será exibido no próximo slide.
- Em seguida, vá para o slide 8 e, com o quadro de resposta projetado, vá mediando o seu preenchimento e inserindo os dados solicitados.
- Confira, em Discuta com a Turma, abaixo, algumas questões provocativas para reflexões acerca do conteúdo em pauta, e as expectativas de respostas dos estudantes, entre parênteses, ponderando a relevância para o seu contexto, no momento.
- Não exceda mais de 5 minutos para esta etapa de análise dos polígonos, reconhecimento dos regulares e preenchimento do quadro-resposta.
- Utilize o slide 9 apenas para dizer que assistirão a um vídeo sobre as condições para os polígonos regulares formarem mosaico.
- Exiba o vídeo, com duração de 2:58 min, para todos e diga que os comentários serão feitos em seguida. Assista ao vídeo aqui.
- Confira, em Discuta com a Turma, abaixo, algumas questões provocativas para reflexões acerca do conteúdo do vídeo, ponderando a relevância.
- Não exceda mais de 3 minutos na discussão sobre o conteúdo do vídeo.
- Vá para o slide 10 e explique que trabalharão em trio e que farão mosaicos regulares.
- Observe se todos estão conectados à internet com o aplicativo GeoGebra.
- Explique que o objetivo da atividade é utilizar o GeoGebra para preencher com polígonos um determinado plano, cobrindo os seus 360º.
- Explique que devem seguir as orientações contidas na própria atividade, mas enfatize que, no GeoGebra, devem usar o ambiente Geometria.
- Observe que, na atividade, é sugerida a exibição de uma malha quadriculada para fazer o desenho, mas que esta escolha é opcional.
- Explique, também, que, a partir do desenho dos polígonos, os trios devem escolher Polígonos Regulares.
- Diga-lhes que estará presente para acompanhar o trabalho dos grupos.
- Explicite que a construção dos mosaicos não deve exceder 15 minutos.
- Imprima previamente a Atividade Principal.
- Considere as seguintes Atividades Complementares, para você ver mais possibilidades pedagógicas para o assunto mosaico com polígonos:
Atividades Complementares ao Professor:
1ª) Para saber mais sobre ladrilhos, sugerimos a leitura do artigo “Ladrilhamentos”, de Elvia Mureb Sallum, da Matemateca do Instituto de Matemática e Estatística da Universidade de São Paulo (IME-USP). Leia o artigo na íntegra, clicando aqui.
2ª) Para conhecer mais sobre mosaicos, leio o material “Mosaicos” do Laboratório de Ensino de Matemática da Universidade de Brasília (LEMAT-UnB), disponível aqui.
3ª) Material complementar do LEMAT-UnB de Solução das atividades com mosaicos”, disponível aqui.
- Lembre-se de que você dispõe de questões provocadoras, no Guia de Intervenção, que pode ser acessado aqui.
- Confira a Atividade Principal, acessando aqui.
Propósito: Fazer composições com polígonos para formar mosaicos regulares.
Discuta com a turma :
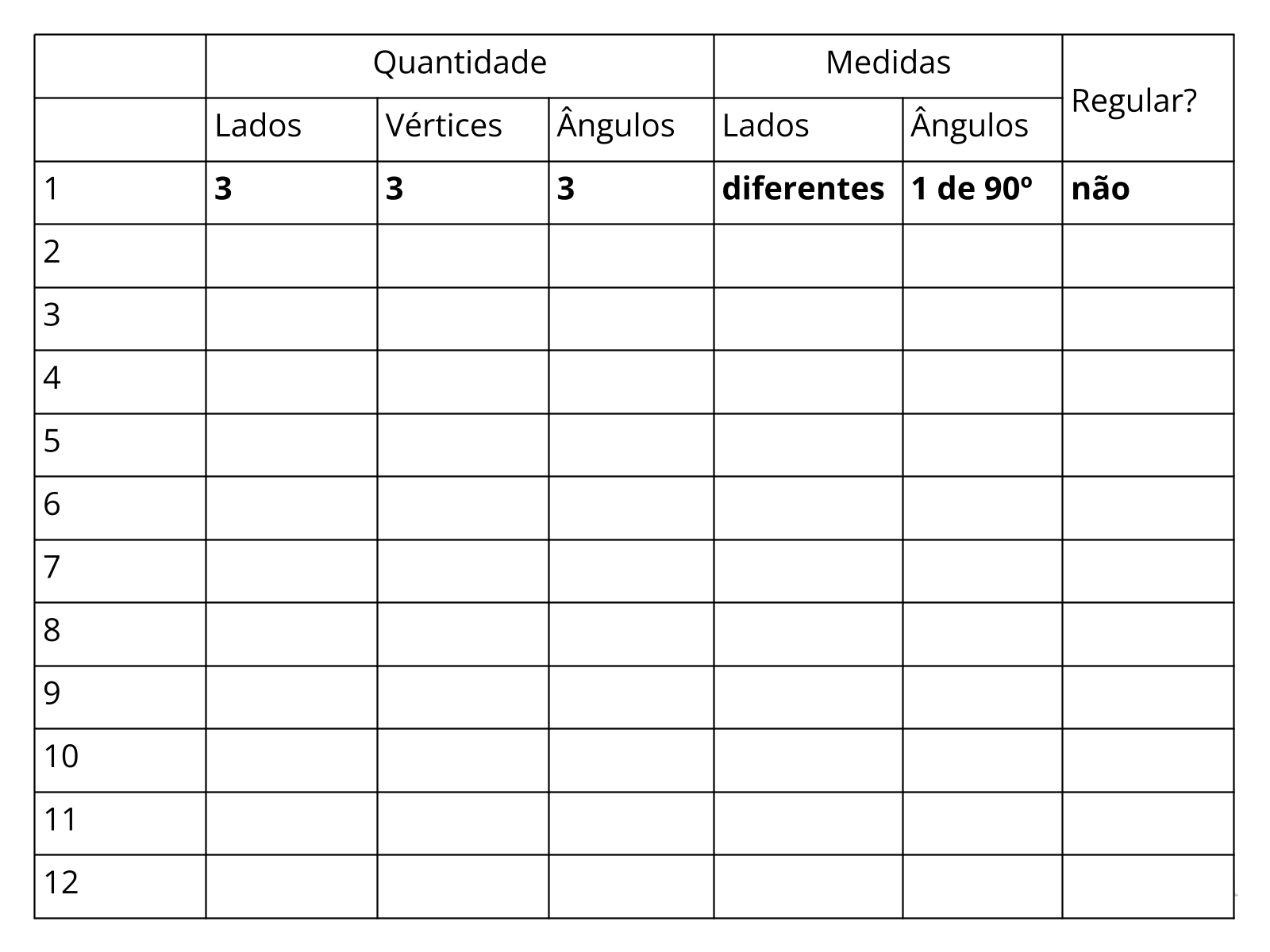
Slide 8:
- Para o polígono ser regular, como deve ser o preenchimento do quadro-resposta?
- Quais das figuras são, portanto, regulares?
Atividade Principal

Tempo sugerido: 25 minutos (slides 6, 7, 8, 9 e 10).
Orientações:
- Utilize o slide 6 para pontuar, brevemente, os 3 momentos da atividade, explicando que os dois primeiros serão cumpridos coletivamente, por toda a turma, e o terceiro, em trios, no GeoGebra.
- Esta aula considera que os estudantes já tiveram algum contato anterior com o GeoGebra, mas se não tiveram, sugerimos que oriente os estudantes, em aulas anteriores, que experimentem o aplicativo em casa e que ele dá 2 opções de uso, on line ou baixando no computador.
- Esta aula deve ser desenvolvida, preferencialmente, em um laboratório de informática, que comporte 3 estudantes por computador, e com um projetor; alternativamente, podem ser usados recursos tecnológicos individuais, com acesso à internet, mas é interessante o projetor, para que sejam realizados os 2 primeiros momentos, coletivamente, com todos da turma.
- Em seguida, vá para o slide 7, utilizando-o para apresentar a proposta do primeiro momento da atividade com toda a turma, de modo coletivo.
- Projete a apresentação do slide 7 para que todos acompanhem e participem; todos devem estar com o mesmo slide em seus computadores.
- Faça mediações para toda a turma, iniciando pela numeração dos polígonos e pela questão por que esses polígonos são regulares, com base em medidas e número de lados, ângulos e vértices, preenchendo o quadro de respostas, que será exibido no próximo slide.
- Em seguida, vá para o slide 8 e, com o quadro de resposta projetado, vá mediando o seu preenchimento e inserindo os dados solicitados.
- Confira, em Discuta com a Turma, abaixo, algumas questões provocativas para reflexões acerca do conteúdo em pauta, e as expectativas de respostas dos estudantes, entre parênteses, ponderando a relevância para o seu contexto, no momento.
- Não exceda mais de 5 minutos para esta etapa de análise dos polígonos, reconhecimento dos regulares e preenchimento do quadro-resposta.
- Utilize o slide 9 apenas para dizer que assistirão a um vídeo sobre as condições para os polígonos regulares formarem mosaico.
- Exiba o vídeo, com duração de 2:58 min, para todos e diga que os comentários serão feitos em seguida. Assista ao vídeo aqui.
- Confira, em Discuta com a Turma, abaixo, algumas questões provocativas para reflexões acerca do conteúdo do vídeo, ponderando a relevância.
- Não exceda mais de 3 minutos na discussão sobre o conteúdo do vídeo.
- Vá para o slide 10 e explique que trabalharão em trio e que farão mosaicos regulares.
- Observe se todos estão conectados à internet com o aplicativo GeoGebra.
- Explique que o objetivo da atividade é utilizar o GeoGebra para preencher com polígonos um determinado plano, cobrindo os seus 360º.
- Explique que devem seguir as orientações contidas na própria atividade, mas enfatize que, no GeoGebra, devem usar o ambiente Geometria.
- Observe que, na atividade, é sugerida a exibição de uma malha quadriculada para fazer o desenho, mas que esta escolha é opcional.
- Explique, também, que, a partir do desenho dos polígonos, os trios devem escolher Polígonos Regulares.
- Diga-lhes que estará presente para acompanhar o trabalho dos grupos.
- Explicite que a construção dos mosaicos não deve exceder 15 minutos.
- Imprima previamente a Atividade Principal.
- Considere as seguintes Atividades Complementares, para você ver mais possibilidades pedagógicas para o assunto mosaico com polígonos:
Atividades Complementares ao Professor:
1ª) Para saber mais sobre ladrilhos, sugerimos a leitura do artigo “Ladrilhamentos”, de Elvia Mureb Sallum, da Matemateca do Instituto de Matemática e Estatística da Universidade de São Paulo (IME-USP). Leia o artigo na íntegra, clicando aqui.
2ª) Para conhecer mais sobre mosaicos, leio o material “Mosaicos” do Laboratório de Ensino de Matemática da Universidade de Brasília (LEMAT-UnB), disponível aqui.
3ª) Material complementar do LEMAT-UnB de Solução das atividades com mosaicos”, disponível aqui.
- Lembre-se de que você dispõe de questões provocadoras, no Guia de Intervenção, que pode ser acessado aqui.
- Confira a Atividade Principal, acessando aqui.
Propósito: Fazer composições com polígonos para formar mosaicos regulares.
Discuta com a turma :
Slide 9 - Discussão para construção do mosaico: questões provocadoras (pertinente à atividade):
- Como cobrir, lado a lado, sem sobrepor?
- Quais características deve ter um polígono para que, unido lado a lado com outros por um mesmo vértice, sirva para cobrir 360º de um tipo qualquer de plano, sem sobreposição?
- Quais polígonos regulares têm essas características e formam um mosaico?
- Quais polígonos regulares não têm essas características e não formam um mosaico?
Atividade Principal
Tempo sugerido: 25 minutos (slides 6, 7, 8, 9 e 10).
Orientações:
- Utilize o slide 6 para pontuar, brevemente, os três momentos da atividade, explicando que os dois primeiros serão cumpridos coletivamente, por toda a turma, e o terceiro, em trios, no GeoGebra.
- Esta aula considera que os estudantes já tiveram algum contato anterior com o GeoGebra, mas se não tiveram, sugerimos que oriente os estudantes, em aulas anteriores, para que experimentem o aplicativo em casa. Há 2 opções de uso: online e baixando no computador.
- Preferencialmente, esta aula deve ser desenvolvida em um laboratório de informática que comporte 3 estudantes por computador, e com um projetor; De forma alternativa, podem ser usados recursos tecnológicos individuais, com acesso à internet. O projetor segue recomendado para que sejam realizados os dois primeiros momentos, com todos da turma.
- Em seguida, vá para o slide 7, utilizando-o para apresentar a proposta do primeiro momento da atividade com toda a turma, de modo coletivo.
- Projete a apresentação do slide 7 para que todos acompanhem e participem; todos devem estar com o mesmo slide em seus computadores.
- Faça mediações para toda a turma, iniciando pela numeração dos polígonos e pela questão por que esses polígonos são regulares, com base em medidas e número de lados, ângulos e vértices, preenchendo o quadro de respostas, que será exibido no próximo slide.
- Em seguida, vá para o slide 8 e, com o quadro de resposta projetado, vá mediando o seu preenchimento e inserindo os dados solicitados.
- Confira, em Discuta com a Turma, abaixo, algumas questões provocativas para reflexões acerca do conteúdo em pauta, e as expectativas de respostas dos estudantes, entre parênteses, ponderando a relevância para o seu contexto, no momento.
- Não exceda mais de 5 minutos para esta etapa de análise dos polígonos, reconhecimento dos regulares e preenchimento do quadro-resposta.
- Utilize o slide 9 apenas para dizer que assistirão a um vídeo sobre as condições para os polígonos regulares formarem mosaico.
- Exiba o vídeo, com duração de 2:58 min, para todos e diga que os comentários serão feitos em seguida. Assista ao vídeo aqui.
- Confira, em Discuta com a Turma, abaixo, algumas questões provocativas para reflexões acerca do conteúdo do vídeo, ponderando a relevância.
- Não exceda mais de 3 minutos na discussão sobre o conteúdo do vídeo.
- Vá para o slide 10 e explique que trabalharão em trio e que farão mosaicos regulares.
- Observe se todos estão conectados à internet com o aplicativo GeoGebra.
- Explique que o objetivo da atividade é utilizar o GeoGebra para preencher com polígonos um determinado plano, cobrindo os seus 360º.
- Explique que devem seguir as orientações contidas na própria atividade, mas enfatize que, no GeoGebra, devem usar o ambiente Geometria.
- Observe que, na atividade, é sugerida a exibição de uma malha quadriculada para fazer o desenho, mas que esta escolha é opcional.
- Explique, também, que, a partir do desenho dos polígonos, os trios devem escolher Polígonos Regulares.
- Diga-lhes que estará presente para acompanhar o trabalho dos grupos.
- Explicite que a construção dos mosaicos não deve exceder 15 minutos.
- Imprima previamente a Atividade Principal.
- Considere as seguintes Atividades Complementares, para você ver mais possibilidades pedagógicas para o assunto mosaico com polígonos:
Atividades Complementares ao Professor:
1ª) Para saber mais sobre ladrilhos, sugerimos a leitura do artigo “Ladrilhamentos”, de Elvia Mureb Sallum, da Matemateca do Instituto de Matemática e Estatística da Universidade de São Paulo (IME-USP). Leia o artigo na íntegra, clicando aqui.
2ª) Para conhecer mais sobre mosaicos, leio o material “Mosaicos” do Laboratório de Ensino de Matemática da Universidade de Brasília (LEMAT-UnB), disponível aqui.
3ª) Material complementar do LEMAT-UnB de Solução das atividades com mosaicos”, disponível aqui.
- Lembre-se de que você dispõe de questões provocadoras, no Guia de Intervenção, que pode ser acessado aqui.
- Confira a Atividade Principal, acessando aqui.
Propósito: Fazer composições com polígonos para formar mosaicos regulares.
Discuta com a turma :
- Slide 10
- Utilize este slide apenas para falar que a atividade no GeoGebra irá começar. As provocações já foram colocadas anteriormente.
Discussão das soluções

Tempo sugerido: 5 minutos.
Orientações:
- Como a atividade foi composta de dois momentos de resultados e um de reflexão e discussão sobre a relação entre o conteúdo do momento 1 (polígonos regulares) e a construção de mosaicos, no momento 3, já houve discussões durante o percurso e a expectativa é que, durante a 2ª atividade, envolvendo todo o grupo, essa discussão tenha sido calorosa e proveitosa de aprendizagens.
- Peça para que quatro trios (essa quantidade é uma sugestão), espontaneamente, apresentem suas produções, mas compartilhe todos os mosaicos.
- Como sugestão, se a escola tiver um site, ou blogue, ou página no Facebook, peça a autorização dos artistas para publicar os mosaicos construídos.
- Durante a exposição dos trios, reforce as questões já mencionadas no Discuta com a Turma dos 4 primeiros slides da Atividade Principal.
- Outras provocações, confira o Guia de Intervenções.
Propósito: Discutir, coletivamente, sobre polígonos regulares e não regulares e sobre a formação de mosaicos regulares ou irregulares.
Discuta com a turma:
- Mostrem-nos por que o seu mosaico é regular.
- Apresentem-nos as características dos polígonos utilizados que justifiquem a sua classificação como regular.
Material Complementar:
Encerramento
Tempo sugerido: 2 minutos.
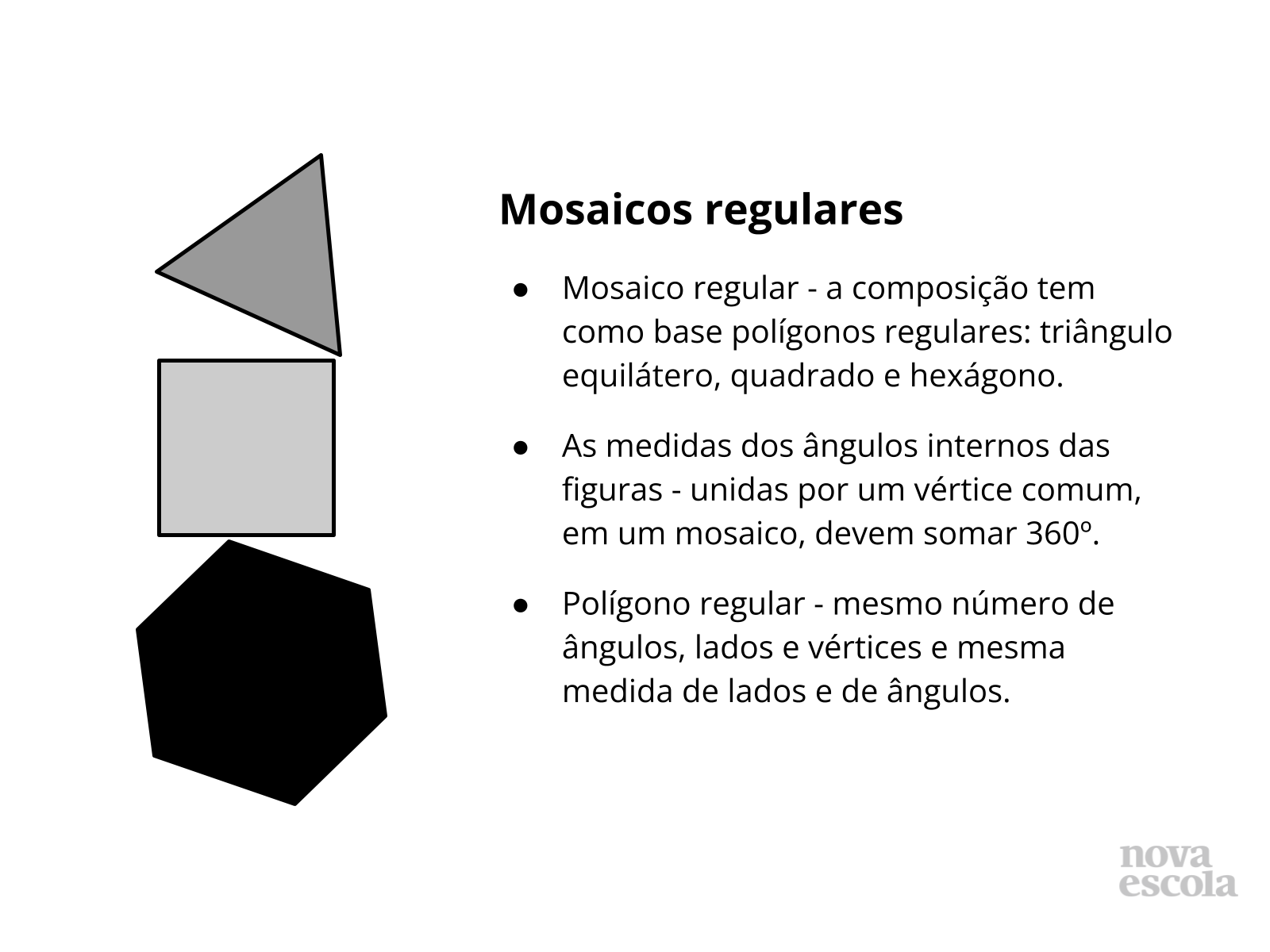
Orientações: Este slide pontua o conteúdo trabalhado e sua apresentação deve ser muito breve. Busque enfatizar as características de um mosaico regular e de sua composição com polígonos regulares.
Propósito: Sintetizar, de modo ilustrativo, o conteúdo trabalhado.
Raio-X

Tempo sugerido: 8 minutos (slides 13 e 14).
Orientações:
- O slide 13 visa a apresentação breve da avaliação.
- Utilize o slide 13 para explicar a atividade, mas não estenda mais de 1 minuto. Imprima, previamente, a atividade (slide 14) para que seja realizada individualmente.
- Sem muito rigor na organização da sala, peça aos estudantes para se afastarem ou se arrumarem separadamente, para uma atividade que exigirá deles reflexão, atenção e conhecimento sobre polígonos regulares e sobre sua pertinência em mosaicos regulares.
Propósito: Demonstrar conhecimentos sobre mosaicos regulares e irregulares e sobre os polígonos que os compõem.
Discuta com a turma:
- Faça provocações de modo que o estudante seja levado a refletir sobre a qualidade da composição de mosaicos regulares a partir do tipo de polígonos que os compõem.
- Diversas provocações estão disponíveis no Guia de Intervenção.
Materiais Complementares:
Resolução da Atividade Complementar
Raio-X
Tempo sugerido: 8 minutos (slides 13 e 14).
Orientações:
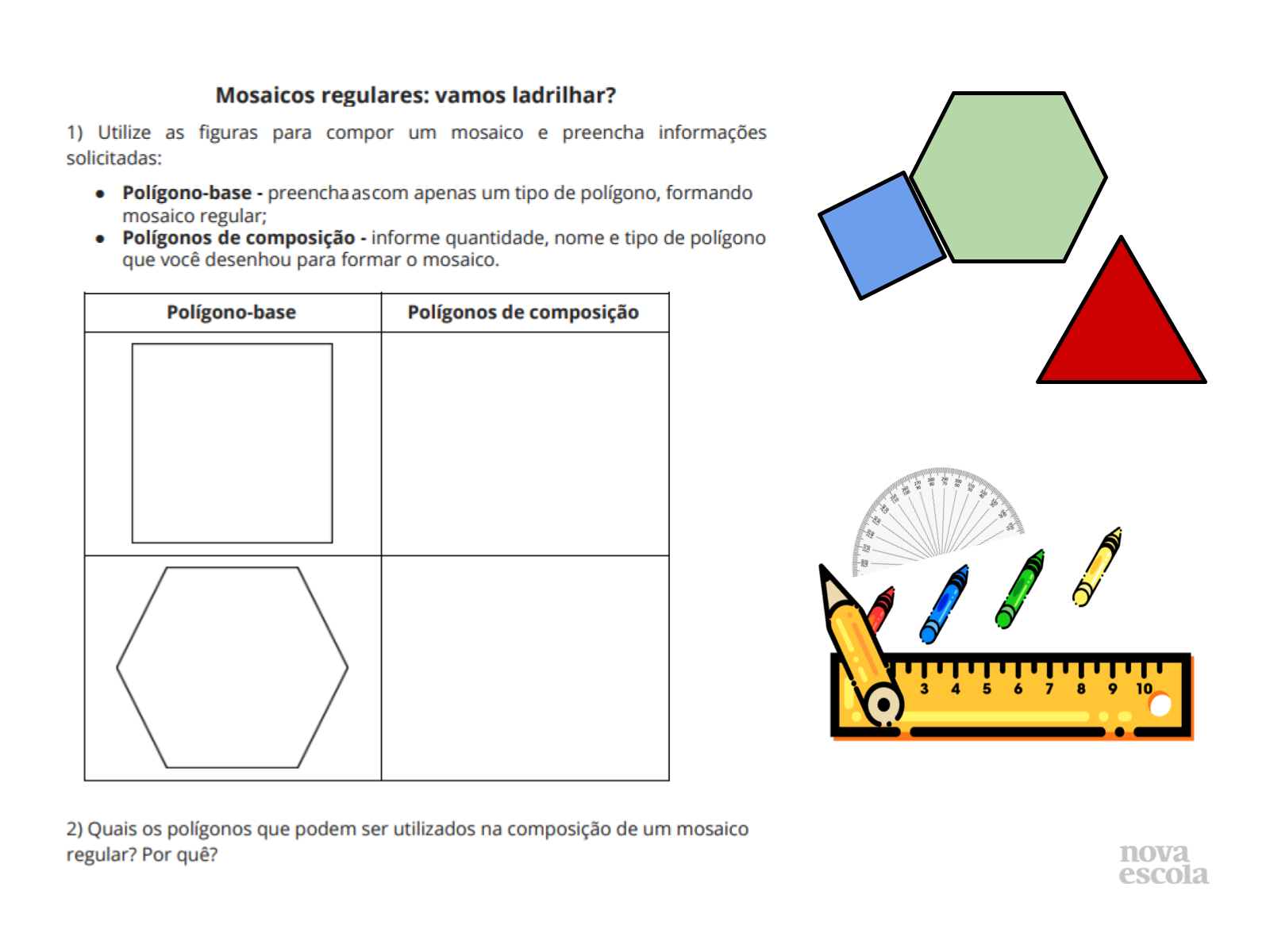
- O slide 13 visa a apresentação breve da avaliação.
- Utilize o slide 13 para explicar a atividade, mas não estenda mais de 1 minuto. Imprima, previamente, a atividade (slide 14) para que seja realizada individualmente.
- Sem muito rigor na organização da sala, peça aos estudantes para se afastarem ou se arrumarem separadamente, para uma atividade que exigirá deles reflexão, atenção e conhecimento sobre polígonos regulares e sobre sua pertinência em mosaicos regulares.
Propósito: Demonstrar conhecimentos sobre mosaicos regulares e irregulares e sobre os polígonos que os compõem.
Discuta com a turma:
- Faça provocações de modo que o estudante seja levado a refletir sobre a qualidade da composição de mosaicos regulares a partir do tipo de polígonos que os compõem.
- Diversas provocações estão disponíveis no Guia de Intervenção.
Para os Alunos
Para o Professor
Sugestão de adaptação para ensino remoto
Código do plano MAT5_17GEO09
Recursos
- Necessários: -
- Opcionais: GeoGebra
Para este plano, foque na etapa Retomada, Atividade principal e Raio X
Retomada
Professor(a), você pode realizar a Retomada deste plano com seus alunos seja em uma aula síncrona ou assíncrona. Compartilhe com a turma os slides presentes nesta atividade. Compartilhe, em formato de texto, os questionamentos presentes no “Discuta com a turma”. Caso a aula esteja ocorrendo de forma síncrona, permita que os alunos exponham suas reflexões; e, caso esteja ocorrendo de forma assíncrona, os estudantes podem enviar suas reflexões em formato de texto ou áudio.
Atividade principal
Professor(a), mesmo que a atividade proponha que sejam formados grupos, isso não é necessário, todos os alunos podem trabalhar na atividade de forma individual. Compartilhe com a turma as instruções para as etapas de realização da atividade: https://nova-escola-producao.s3.amazonaws.com/8C34mNbBXt7pgvpdXTJ99GjS3JJrt3QUChVXjP7AYjBEVvkXsWSM3CP3SvwV/ativaula-mat5-17geo09.pdf
No 1º momento, oriente que os alunos enumerem os polígonos e os classifiquem. Não é necessário que os alunos reproduzam os desenhos em seus cadernos. Oriente que os alunos reproduzam o quadro em seus cadernos e o complete.
No 3º momento, caso não seja possível a criação no software GeoGebra, sugira que os estudantes desenhem em seus cadernos - você pode dar sugestões de imagens buscando a expressão “Pavimentação Matemática” no Google.
Compartilhe, em formato de texto, os questionamentos presentes no “Discuta com a turma”. Caso a aula esteja ocorrendo de forma síncrona, permita que os alunos exponham suas construções e ideias. Caso a aulas esteja ocorrendo de forma assíncrona, os estudantes podem enviar suas soluções em formato de imagens ou vídeos.
Encerramento
Professor(a), solicite que os alunos registrem em seus cadernos a conclusão que chegaram em relação a criação de mosaicos regulares. Caso considere viável, compartilhe com os estudantes os slides presentes nesta etapa do plano de aula.
Raio X
O problema proposto no Raio X pode ser enviado aos alunos e solicitado como uma “tarefa” a ser entregue em momento a ser combinado com a turma. Solicite que os alunos reproduzam o quadro em seus cadernos e o complete. Os estudantes podem fotografar suas resoluções e as compartilhar no ambiente que estejam utilizando para interação com a turma.
Obs.: Você pode realizar uma troca caso a aula esteja ocorrendo de forma síncrona. Realize a atividade presente no Raio X e solicite que a atividade presente na Atividade principal seja realizada como tarefa.
Convite às famílias
Professor(a), sugira que os alunos socializem com seus familiares o que aprenderam nesta aula sobre mosaicos regulares. Uma sugestão de atividade é que os alunos convidem seus familiares a realizarem a atividade proposta na Atividade principal de forma conjunta, pensando em diferentes composições de mosaicos.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA.
Autora: Olenêva Sanches Sousa
Mentora: Paula Massi Reis Pires
Revisora Pedagógica: Eliane Zanin
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
EF5MA17: Reconhecer, nomear e comparar polígonos, considerando lados, vértices e ângulos, e desenhá-los, utilizando material de desenho ou tecnologias digitais.
Objetivos específicos
- Retomar o conceito de polígonos, na perspectiva de composições de mosaicos regulares;
- Fazer composições com polígonos regulares para formar mosaicos regulares;
- Discutir, coletivamente, sobre polígonos regulares e suas possibilidades de formação de mosaicos regulares;
- Pontuar características dos mosaicos regulares;
- Compor mosaicos regulares, reconhecendo os polígonos que os compõem.
Conceito-chave
Mosaicos regulares.
Recursos necessários
- Quadro e pincel;
- Computador;
- Projetor;
- GeoGebra;
- Impressora;
- Internet;
- Atividades impressas da atividade principal - 3º momento (uma cópia para cada trio);
- Atividade raio x (uma cópia por estudante);
- Apresentação dos 5 slides da Atividade Principal (para ser colocada nos computadores de uso discente e para serem projetadas quando em trabalhos coletivos, como nos momentos 1, especialmente, e 2);
- Cronômetro.