Guia de intervenções
Plano de Aula
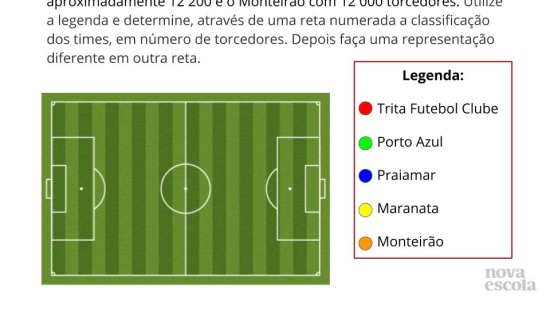
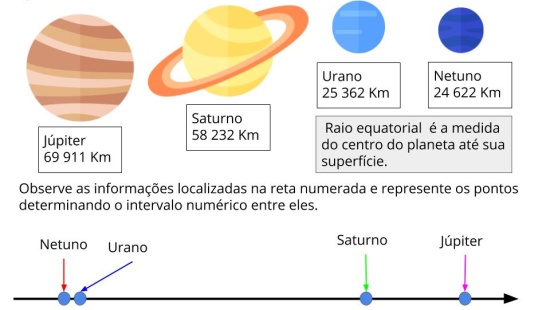
Plano de aula: Ordenação e Sequência numérica com números de 5 ordens
Plano 4 de uma sequência de 5 planos. Veja todos os planos sobre Uma nova ordem: dezena de milhar
Por: Cíntia Diógenes
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Cíntia Diógenes
Mentora: Elisa Greenhalgh Vilalta
Revisora Pedagógica: Eliane Zanin
Especialista de área: Luciana Tenuta
Habilidade da BNCC
EF04MA01 - Ler, escrever e ordenar números naturais até a ordem de dezenas de milhar.
Objetivos específicos
Comparar os números naturais de até cinco ordens utilizando os sinais > e <; Ordenar números de forma crescente;
Identificar padrões em sequências numéricas.
Conceito-chave
Sistema de Numeração Decimal; Reconhecimento; comparação; > ou <.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não;
- Projetor ( opcional).
Habilidades BNCC:
Objetivos de aprendizagem
Comparar os números naturais de até cinco ordens utilizando os sinais > e <; Ordenar números de forma crescente;
Identificar padrões em sequências numéricas.

Precisa de ajuda para criar uma aula personalizada?
Crie seu plano de aula em menos de um minuto no WhatsApp.