Resumo da aula
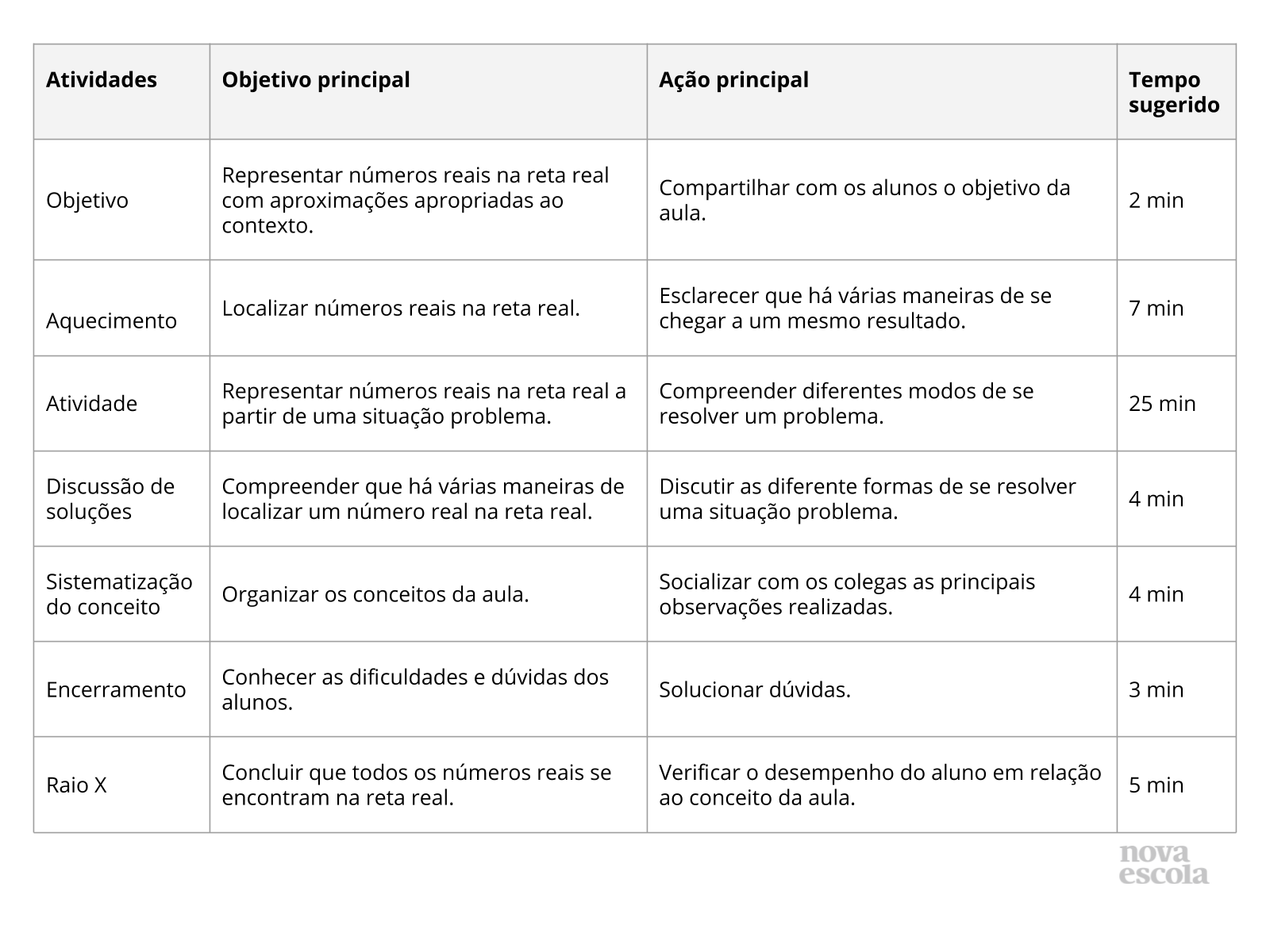
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Apresentar o objetivo aos alunos.
Propósito: Os alunos devem saber o que será aprendido na aula e qual o papel que terão nela.
Discuta com a turma:
- O objetivo da aula e o que se espera dos alunos nessa aula.
Aquecimento

Tempo sugerido: 7 minutos
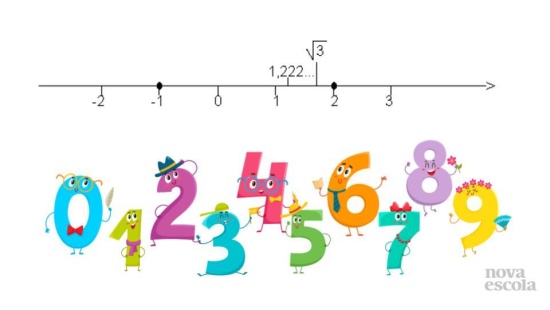
Orientação: Leia a atividade com os alunos e solicite que eles solucionem o que foi proposto. A ideia é que eles conheçam várias formas de chegar ao resultado.
Propósito: Compreender que há várias maneira de localizar um número real na reta numerada.
Discuta com a turma: As respostas da atividade:
- 1 - Verdadeira, quando tentamos chegar ao resultado por aproximação a localização nunca será exata.
- 2 - Falsa, se raiz quadrada de dois é um número infinito não podemos pegar o primeiro decimal e localizar como exata, para que essa resposta se torne verdadeira podemos afirmar que 1,4 é a localização aproximada de raiz quadrada de 2.
- 3 - Verdadeira, podemos localizar raiz quadrada de 2 por aproximação.
Materiais complementares para impressão:
Atividade de Aquecimento
Resolução da Atividade de Aquecimento
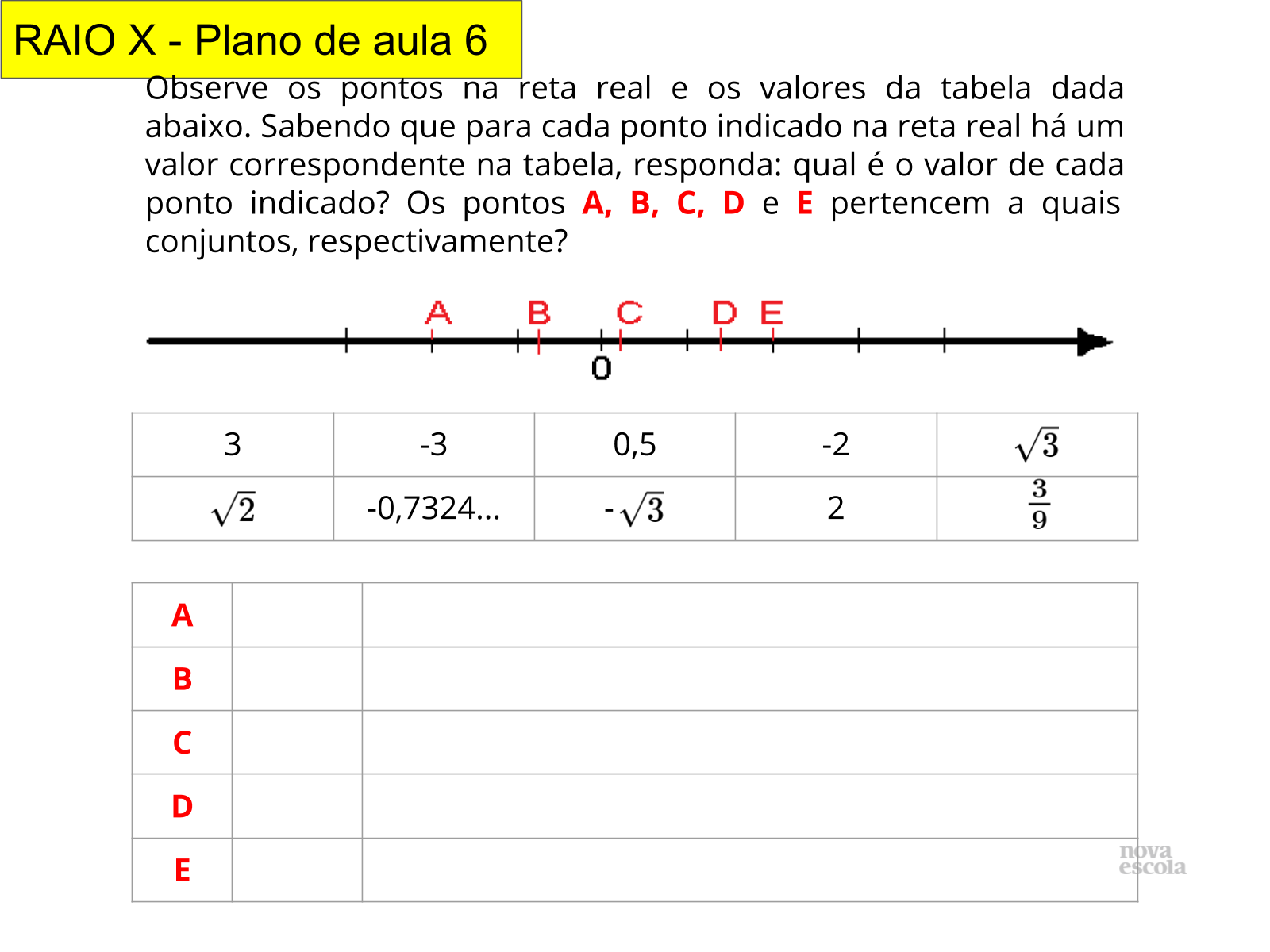
Atividade principal
Tempo sugerido: 25 minutos (slides 4 ao 10)
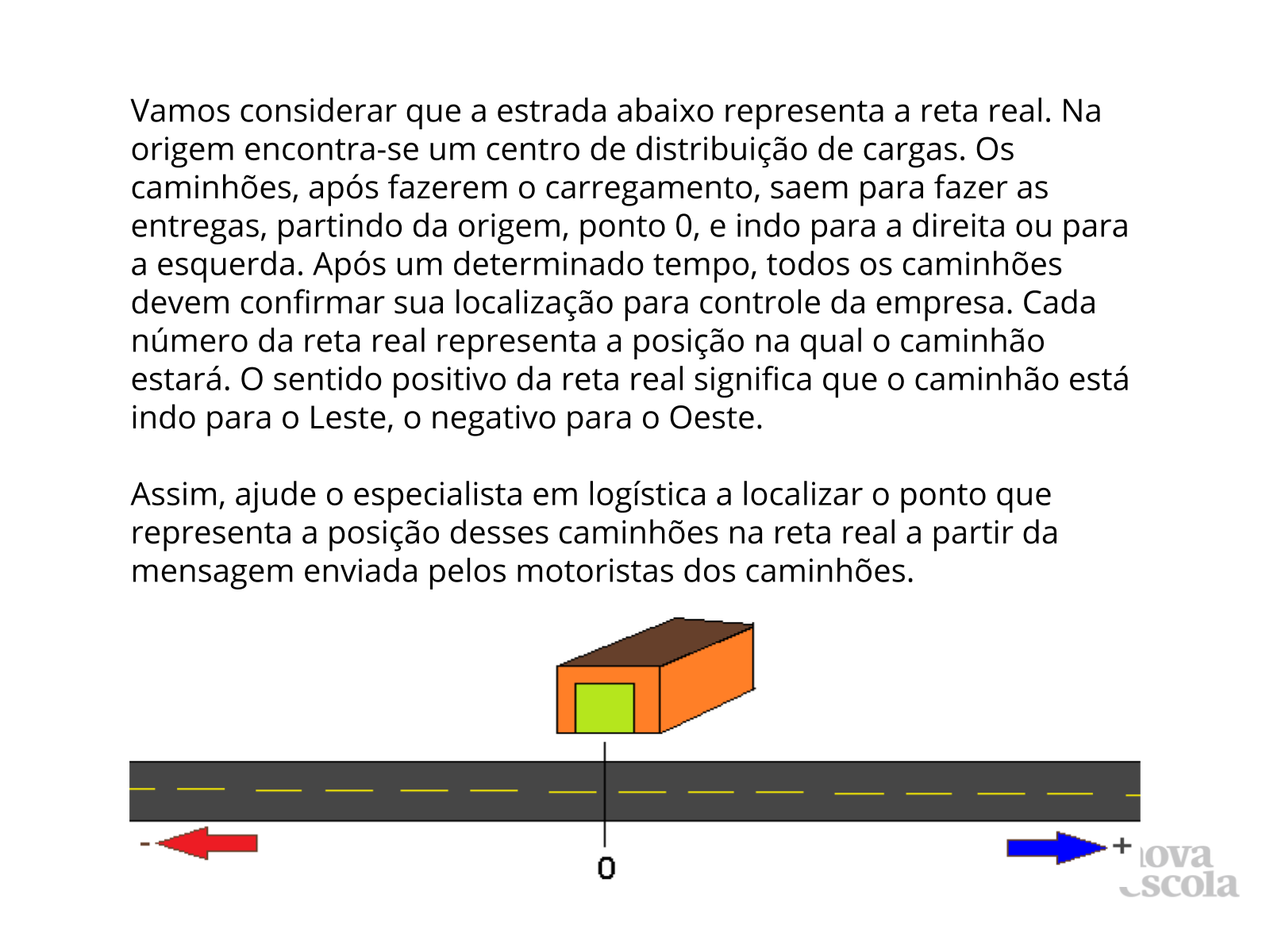
Orientação: Neste momento você professor(a), pode ler o enunciado junto com os alunos.
Propósito: Interpretar o enunciado que dá sentido à toda atividade principal, que é trabalhar com números reais na reta real.
Discuta com a turma:
- Pergunte se há alguma dúvida em relação ao enunciado e às direções Leste e Oeste.
Materiais complementares para impressão:
Atividade Principal
Resolução da Atividade Principal
Guia de Intervenção
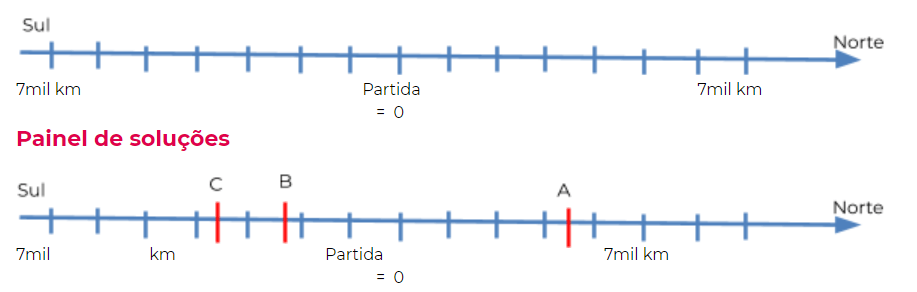
Atividade principal
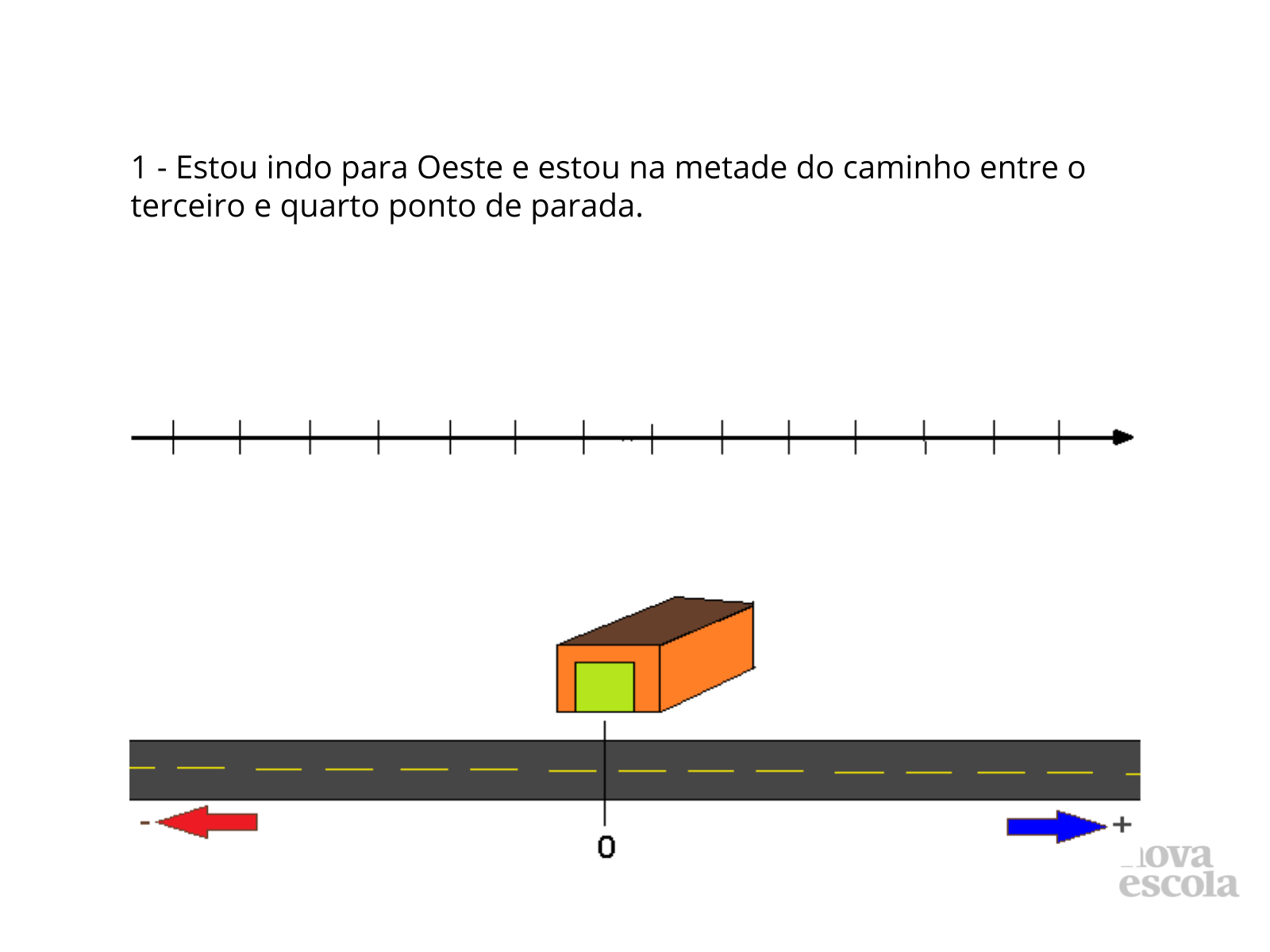
Tempo sugerido: 25 minutos (slides 4 ao 10)
Orientação: Se o motorista está na metade do caminho entre a terceira e quarta cidade, o ponto a ser localizado é -3,5, um número racional e real, decimal finito. Lembrando que, se está indo para Oeste o sinal é negativo.
Propósito: Localizar número real, na reta real, aqui na forma decimal finita, sendo um número racional.
Discuta com a turma: Faça as seguintes perguntas aos seus alunos:
- O número encontrado pertence a quais conjuntos?
- A localização desse caminhão foi exata ou aproximada?
- Sendo um número racional, como posso localizar com exatidão? (Aqui espera-se que o aluno perceba que nem todos os números racionais são localizados na reta real por aproximação, neste caso podemos localizar com exatidão)
- Quais são as dificuldades para localizarmos esse número na reta real?
Atividade principal
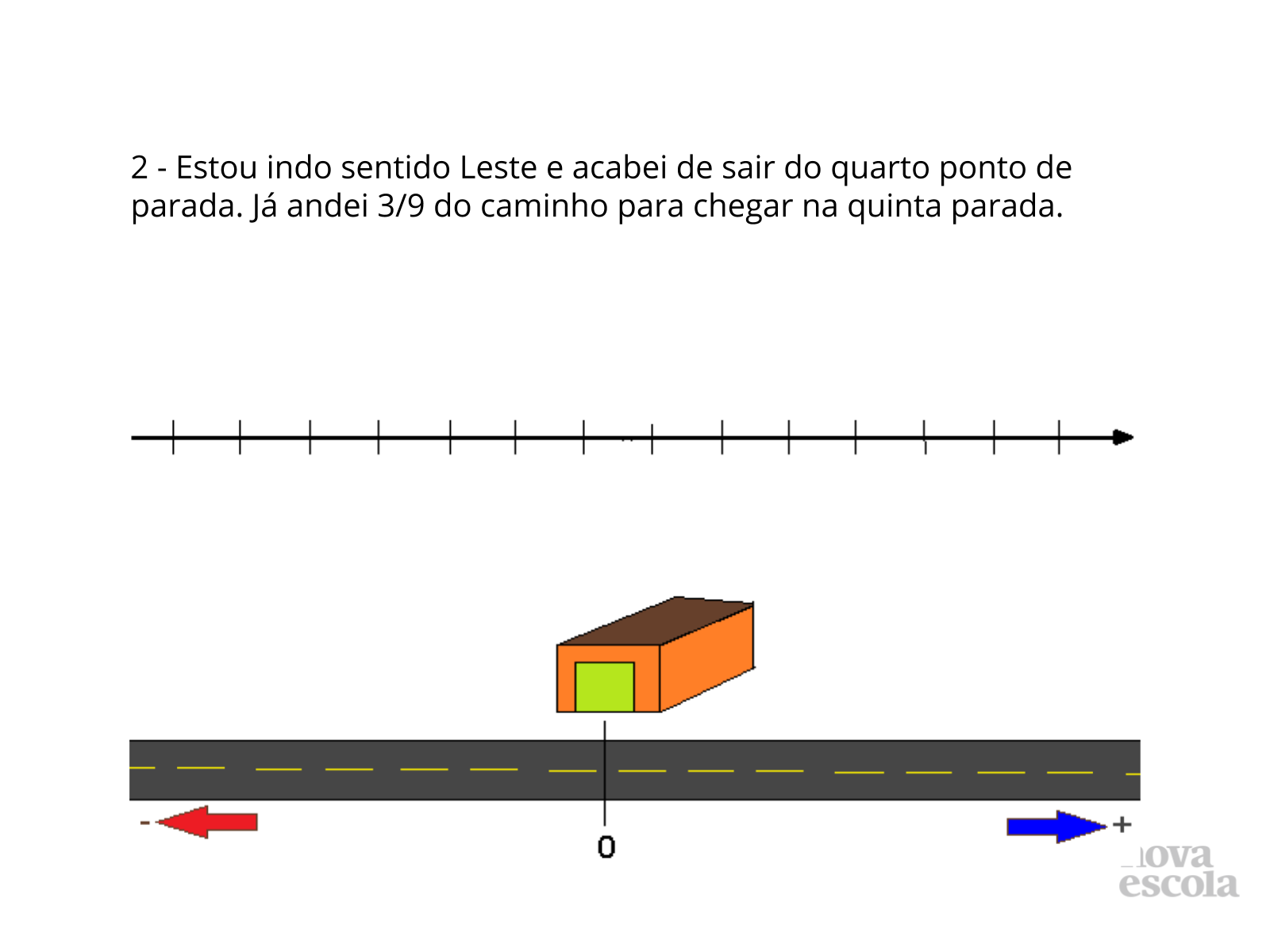
Tempo sugerido: 25 minutos (slides 4 ao 10)
Orientação: Se vai chegar à quinta cidade significa que está entre a quarta e quinta: número inteiro 4 + 3/9 = 4,333…, sendo um número decimal infinito e com período, temos aqui um número racional em forma de dízima periódica, a localização na reta real não será exata e sim aproximada.
Propósito: Localizar número real, na reta real, na forma de dízima periódica, sendo um número racional..
Discuta com a turma: Faça as seguintes perguntas aos seus alunos:
- Quais são as dificuldades para localizarmos esse número na reta real?
- A localização desse caminhão foi exata ou aproximada?
Atividade principal
Tempo sugerido: 25 minutos (slides 4 ao 10)
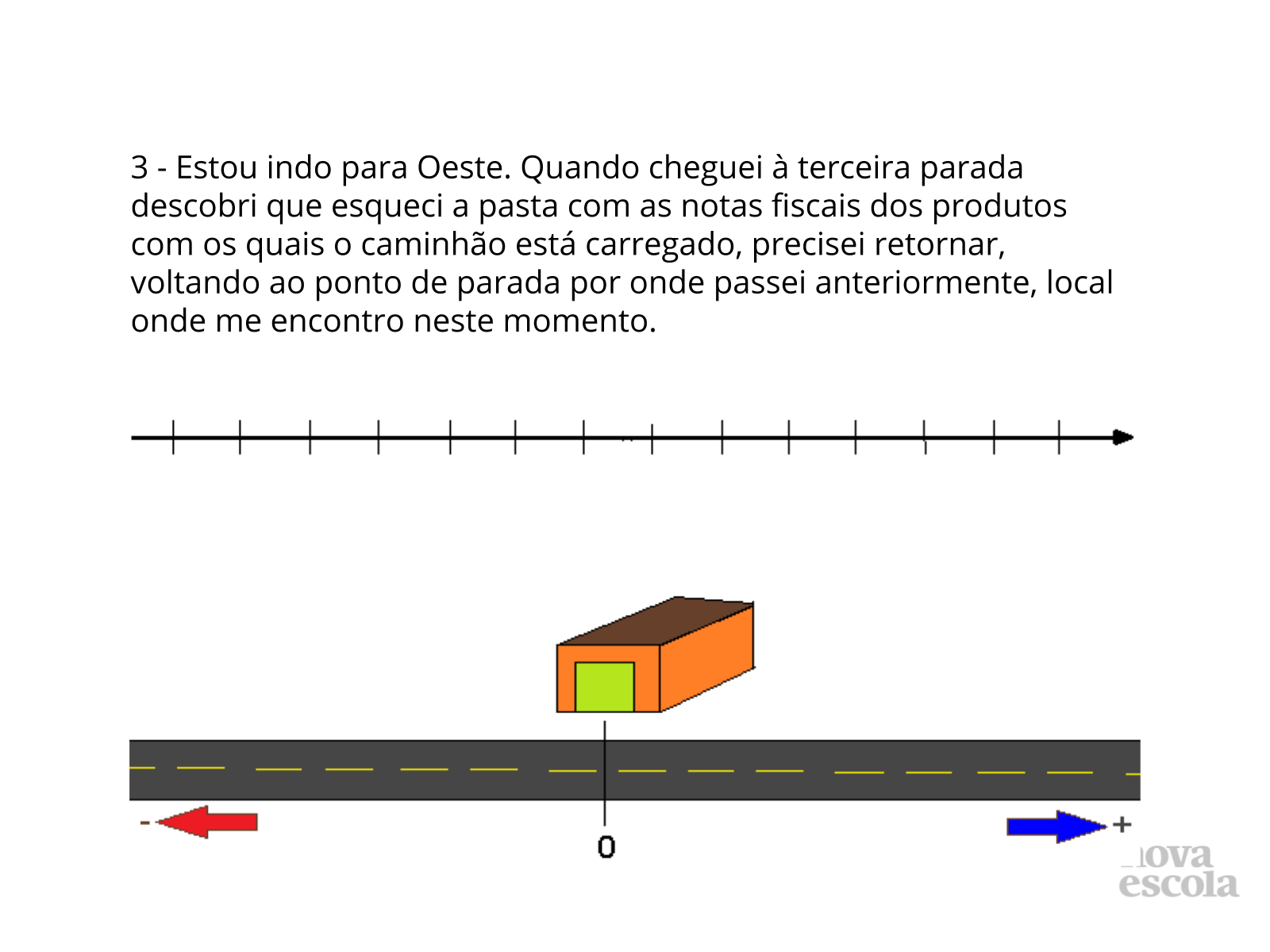
Orientação: Se estava na terceira e voltou para segunda e se encontra lá, a localização é Oeste 2, ou seja -2.
Propósito: Localizar número real, na reta real, aqui na forma de número inteiro negativo.
Discuta com a turma: Faça as seguintes perguntas aos seus alunos:
- Houve dificuldade para localizar esse número na reta real?
- Foi possível localizar o caminhão com exatidão ou por aproximação?
Atividade principal
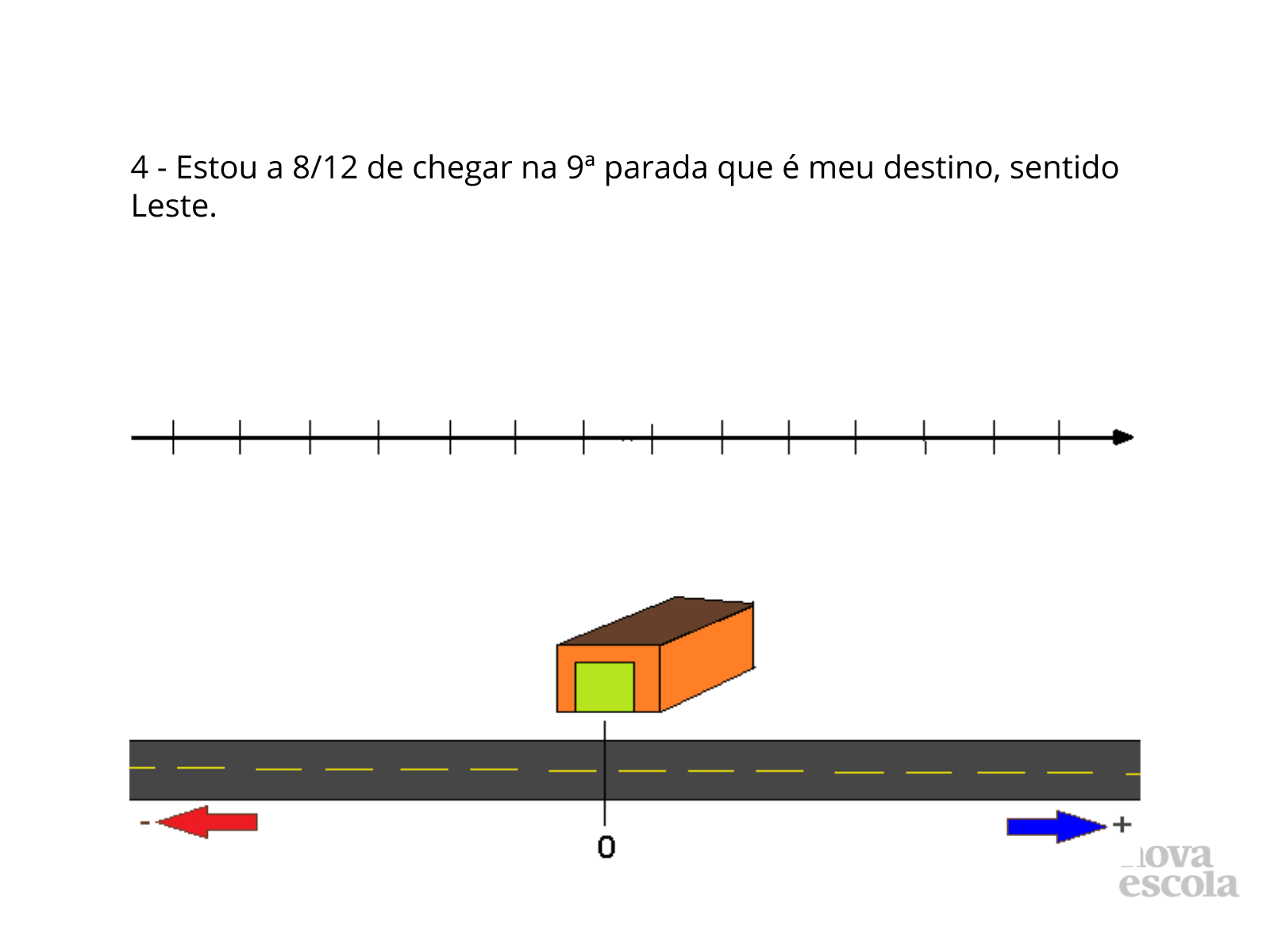
Tempo sugerido: 25 minutos (slides 4 ao 10)
Orientação: 12/12 = 9ª parada, 8/12 = faltam 6 paradas, portanto ele está 4/12 = 3ª parada.
Propósito: Localizar número real, na reta real, aqui na forma de fração, sendo um número racional.
Discuta com a turma: Faça as seguintes perguntas aos seus alunos:
- Quais são as dificuldades para localizarmos esse número na reta numerada?
- A localização desse caminhão foi exata ou aproximada?
Atividade principal
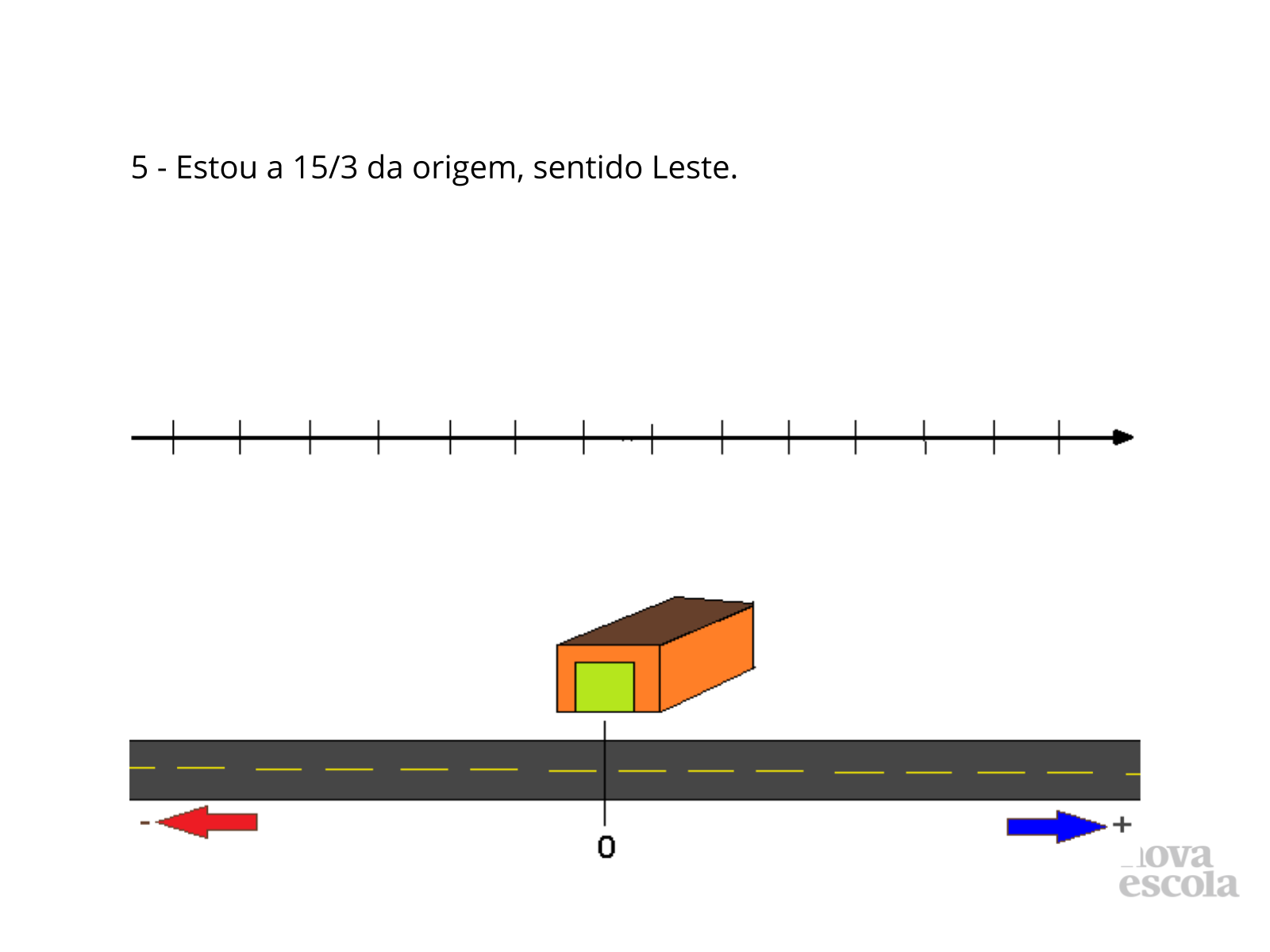
Tempo sugerido: 25 minutos (slides 4 ao 10)
Orientação: Se está à 15/3 da origem, sentido Leste, significa que está na quinta cidade.
Propósito: Localizar número real, na reta real, aqui na forma de número natural.
Discuta com a turma:Faça as seguintes perguntas aos seus alunos:
- Quais são as dificuldades para localizarmos esse número na reta numerada?
- A localização desse caminhão foi exata ou aproximada?
Atividade principal

Tempo sugerido: 25 minutos (slides 4 ao 10)
Orientação:
- Raiz quadrada de 30 = 5,472255…, essa é a localização do posto onde o caminhão se encontra. Sendo um número infinito e não periódico, portanto irracional e real, a localização será aproximada.
- 5 < 5,472255… < 6 , portanto, a 5ª parada é a anterior de onde ele se encontra e a 6ª será a próxima parada. Na reta numerada dos números reais vamos chamar de ponto A a 5ª parada e ponto B a 6ª parada.
- Raiz quadrada de 30 = 5,472255…
Raiz quadrada de 20 = 4,472135…
Se 5,472255… (local onde o caminhão se encontra) e 4,472135… é o que falta para chegar, vamos somar as duas distâncias e chegaremos à resposta que é o destino do caminhão.
Portanto 5,472255… + 4,472135…= 9,944390… assim, encontramos o destino que é a 10ª parada, pois os valores fornecidos são aproximados e 9,944390… está muito próximo de 10.
Propósito: Localizar número real na reta numerada, aqui na forma de número irracional.
Discuta com a turma: Faça as seguintes perguntas aos seus alunos:
- Quais são as dificuldades para localizarmos esse número na reta real?
- A localização desse caminhão foi exata ou aproximada?
Discussão das soluções
Tempo sugerido: 4 minutos
Orientação: Momento de socializar o aprendizado da aula, peça aos alunos que falem sobre o que aprenderam.
Se achar que ainda há tempo hábil para mais uma atividade, a sugestão é que use atividade complementar.
Propósito: Discutir as diversas maneiras de localizar números reais na reta real.
Discuta com a turma:
- Oriente sobre as dificuldades a partir da fala dos alunos.
Encerramento
Tempo sugerido: 4 minutos
Orientação: Utilize o guia de intervenção para discutir com os alunos as dúvidas mais frequentes.
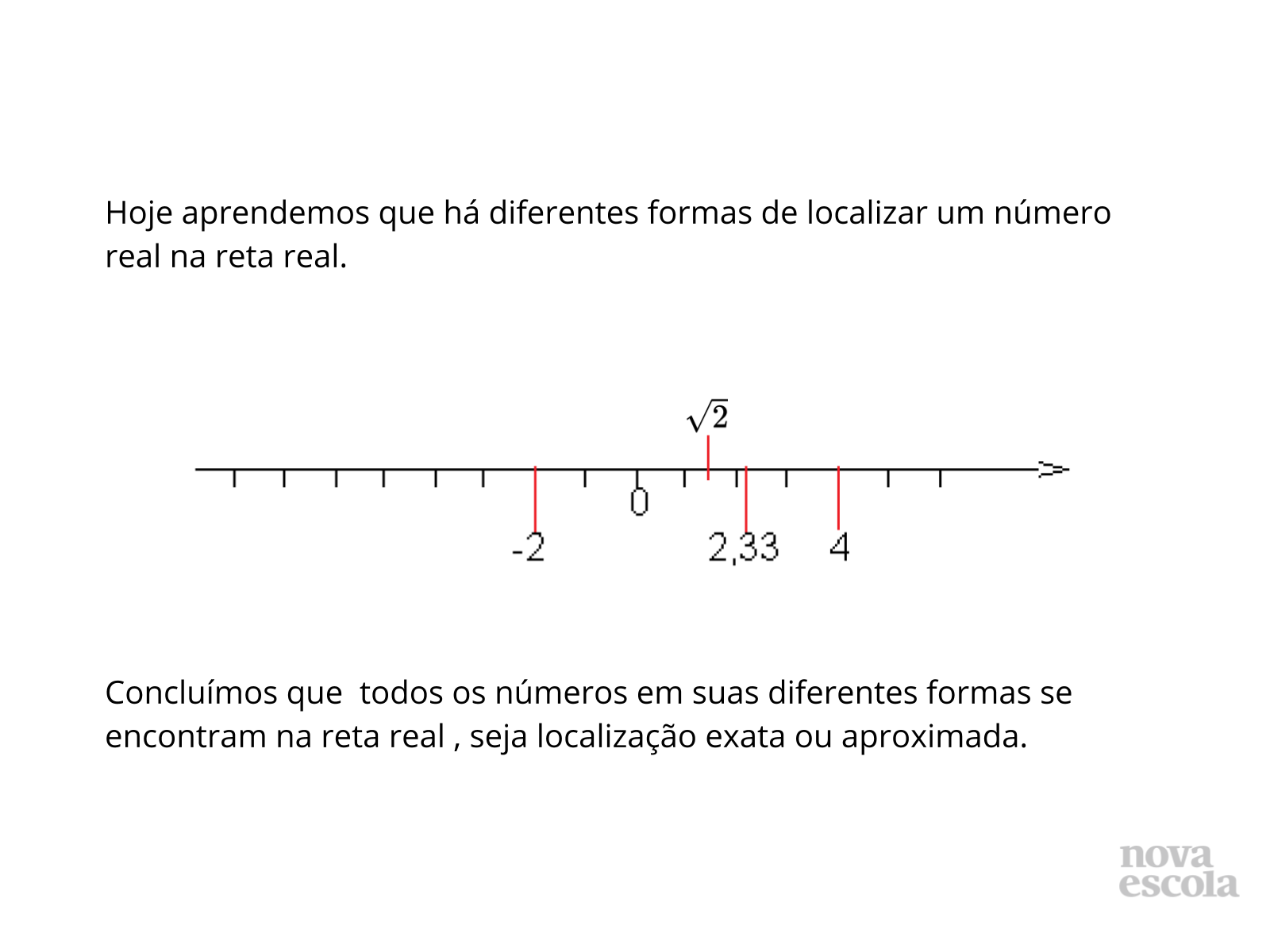
Propósito: Concluir que todos os números reais se encontram na reta real.
Discuta com a turma:
- Pergunte se ainda há alguma dúvida sobre localizar números reais na reta real.
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.