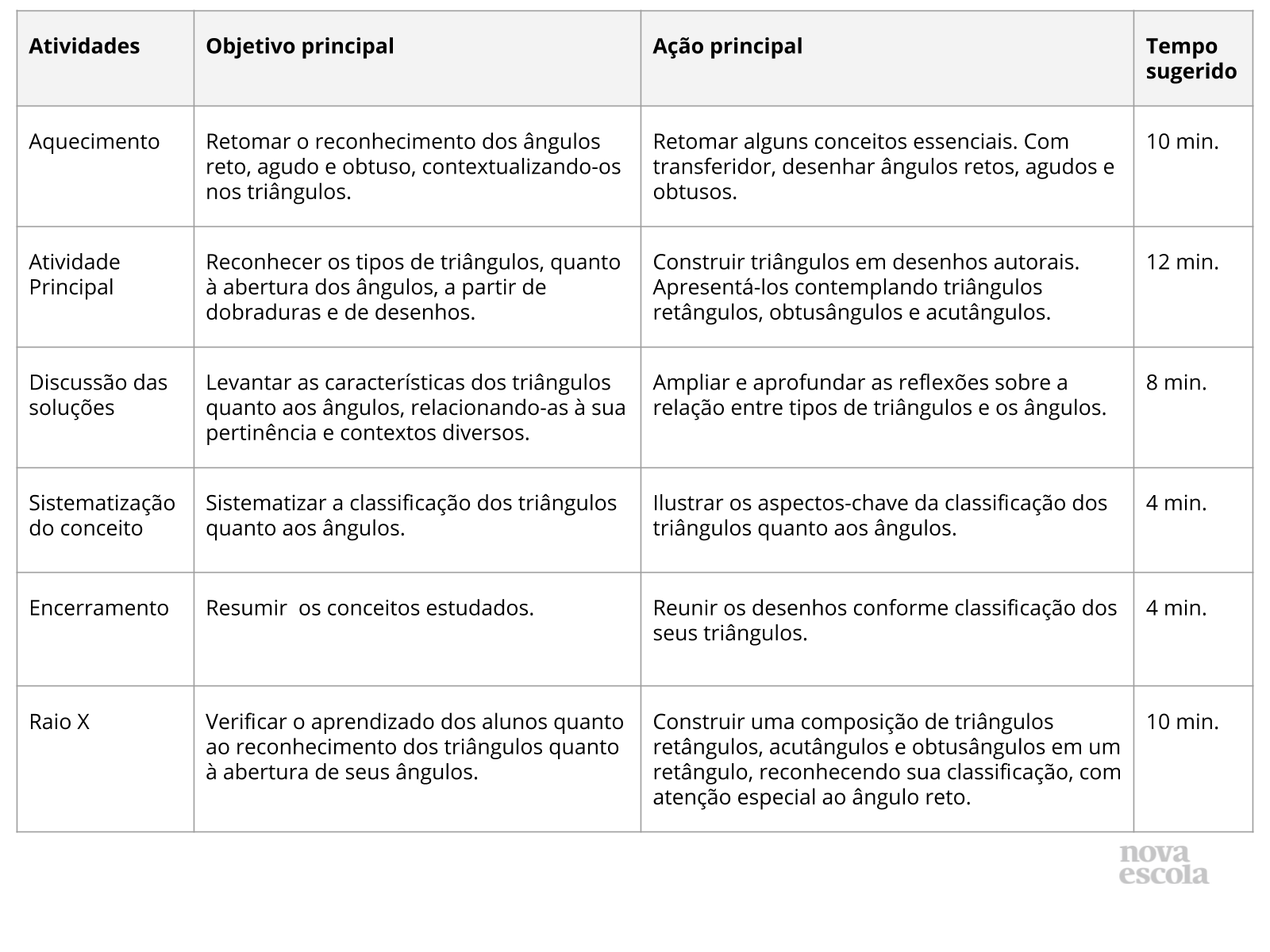
Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
- Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
- Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
- Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
- Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.”
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento
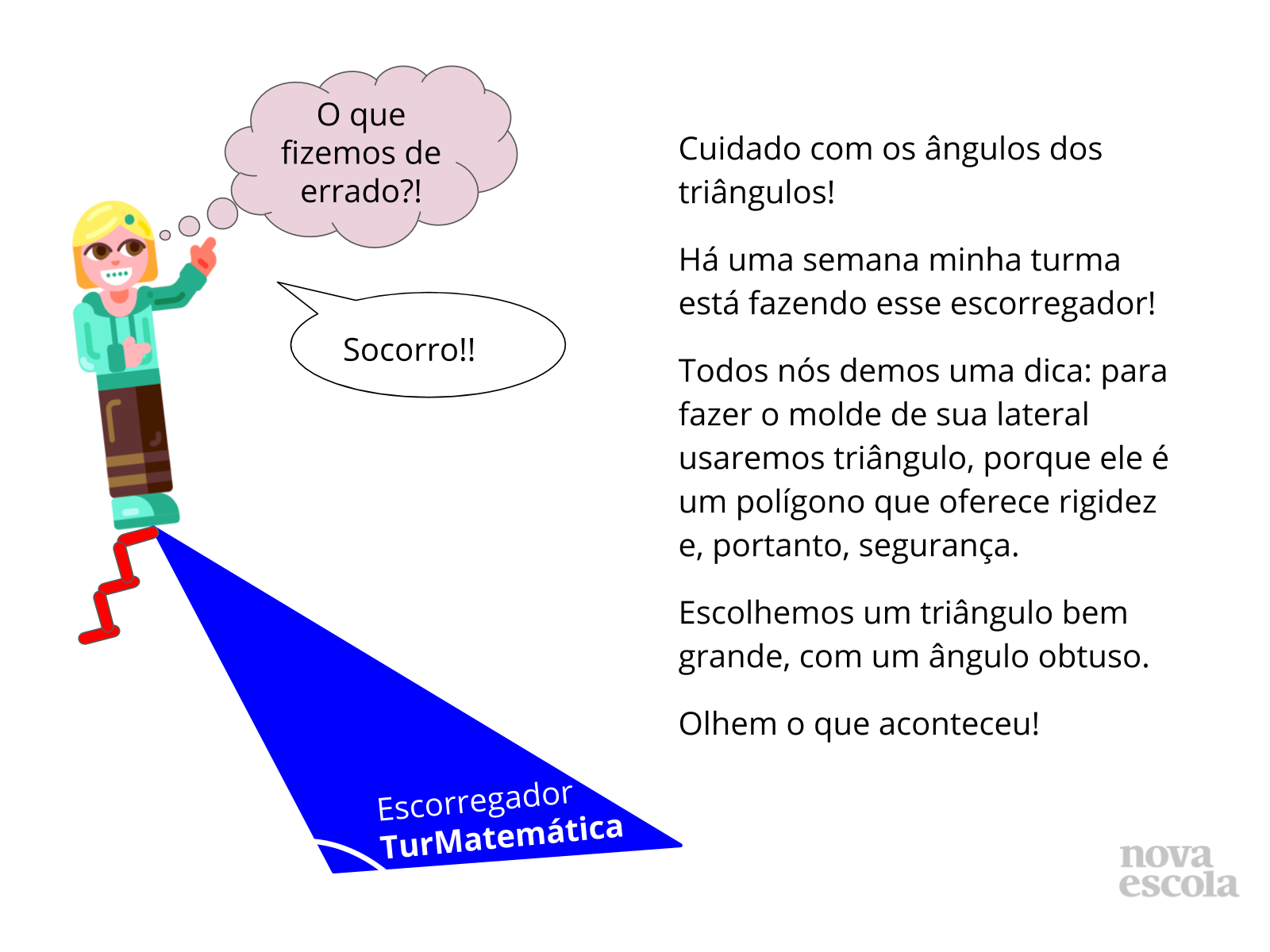
Tempo sugerido: 10 minutos, sendo 5 min para aquecimento de retomada dos conceitos essenciais (ângulos, tipos, retos e não retos, tipos, nomenclatura, triângulo, vértices, lados, ângulos) e 5 minutos para aquecimento de reflexões sobre a construção de triângulos, de olho nos seus ângulos.
Orientações:
- Leia ou peça para um dos estudantes ler o texto da apresentação, fazendo uma mediação provocativa de reflexões acerca de como a avaliação dos ângulos do triângulo é importante.
- Esse aquecimento deve ser bem dinâmico, participativo e rápido, e muitas das questões provocativas, contidas nesta orientação, são pertinentes ao Guia de Intervenções.
Aquecimento de retomada dos conceitos essenciais:
- Desenhe com esquadro, no quadro, 1 triângulo retângulo, com vértices e ângulos marcados, buscando reconhecer, com sua turma, os ângulos a partir dos seus nomes, seus vértices correspondentes, nomes dos triângulos pelos vértices, o ângulo reto.
- Aumente (ou diminua) a abertura do ângulo reto, tornando-o obtuso (ou agudo) para buscar o reconhecimento dos ângulos não retos nos triângulos; ângulos iguais, maiores e menores que 90º, nos triângulos.
Aquecimento de reflexões sobre a construção de triângulos, de olho nos seus ângulos:
- Você deve ilustrar os 3 tipos de triângulos a partir de uma construção dialogada, tendo o ângulo reto como referência.
- Explique à turma que você contará com a ajuda deles na construção de triângulos e que todo mundo deve ficar de olho nos ângulos.
- Lembre-se de, também, fazer os triângulos a partir de papéis dobrados, enfatizando a referência ao ângulo reto.
- Para ver questões provocativas, confira o Guia de Intervenções.
Propósito: Provocar reflexão acerca da importância dos ângulos dos triângulos;
Discuta com a turma:
Aquecimento de retomada dos conceitos essenciais: Nesta apresentação, que se constitui em uma retomada do conteúdo de ângulos, mas inova no contexto dos triângulos, você pode fazer questões envolvendo a compreensão dos ângulos no triângulo, como:
- Onde está o ângulo reto? Qual o seu valor? Como ele é indicado?
- É possível um triângulo ter mais de um ângulo reto? Por quê?
- Então, há um tipo de triângulo que apresenta apenas um ângulo reto?
- Onde está o ângulo maior que 90º? Como ele se chama?
- É possível um triângulo ter mais de um ângulo maior que 90º? Por quê?
- Então, há um tipo de triângulo que apresenta apenas um ângulo obtuso?
- Onde está o ângulo menor que 90º? Como ele se chama?
- É possível um triângulo ter mais de um ângulo menor que 90º? Quantos? Por quê?
- Então, há um tipo de triângulo que apresenta todos os ângulo agudos?
Materiais Complementares:
Você gostaria de ampliar suas concepções sobre o ensino da geometria e, especialmente, sobre o desenvolvimento do pensamento geométrico? Como atividade complementar para você, leia, no capítulo 21, “O pensamento e os conceitos geométricos”, os tópicos “Objetivos de geometria para o aluno” (p. 438-439) e “O desenvolvimento do pensamento geométrico” (p. 439-445), do livro “Matemática no ensino fundamental: formação de professores e aplicação em sala de aula”, de John A. Van de Walle, que você pode acessar na íntegra, clicando aqui. Confira referência completa:
VAN DE WALLE, John A. Matemática no ensino fundamental: formação de professores em sala de aula. Tradução de Paulo Henrique Colonese. 6. ed. Porto Alegre : Artmed, 2009. Disponível em: <https://drive.google.com/file/d/0Bx-KDWmvMaBvcWhydkwxRk5VNUo0TDNoZGhrVU9QVkdKaDZr/view>. Acesso em: 18 nov.2017.
Aquecimento de reflexões sobre a construção de triângulos, de olho nos seus ângulos: Mostre o transferidor de madeira e reapresente-o, brevemente, à turma, questionando sobre o seu uso como instrumento de medida de ângulos, como:
- para fazer um ângulo de triângulo, em que ponto do transferidor devemos começar?
- Onde devo posicionar o ponto zero do transferidor?
- Algum voluntário pode me ajudar na construção, posicionando o transferidor corretamente?
- Se eu quero marcar o ângulo reto, onde está esse ângulo no transferidor?
Observação: Lembre-se de deixar prontos 3 ângulos retos, partindo de 3 segmentos de reta iniciais e inicie as provocações para a construção de triângulos, pelo ângulo reto, como:
- Mas nós queremos construir triângulos, o que podemos fazer agora para desenhá-lo a partir desse ângulo?
- Desenhamos um triângulo que tem um ângulo reto. Este triângulo pode ter outro ângulo reto? Por quê?
- Vamos aumentar o tamanho desse lado?
- O que acontece com o ângulo reto? E com os outros ângulos? Ele continua com o ângulo reto?
- Vamos dobrar um triângulo com um ângulo reto usando um pedaço de papel?
- Vamos testar, com o transferidor se o ângulo dobrado é mesmo reto?
Observação: A partir dos 3 triângulos retângulos desenhados, sobreponha as outras ideias que advierem das mediações para a construção de triângulos, por exemplo, obtusângulos, atentando que essa nomenclatura não deve ser apresentada aos estudantes, nesse momento. A mediação pode ocorrer a partir de várias provocações:
- E se eu abrir mais esse ângulo, ele ainda é reto? Como ele se chama?
- E se eu abrir muito o meu ângulo (passe dos 180º)? Como ficaria o meu triângulo?
- Por que vocês acham que não é possível fazer um triângulo, nesse caso?
Observação: Após escolher qualquer ângulo maior que 90º, continue questionando e construindo, com ajuda de voluntários e considerando opiniões, formando um triângulo:
- É possível haver mais de um ângulo obtuso em um triângulo? Por quê?
- E se eu aumentar o tamanho desse lado, ele continua com o ângulo obtuso?
- Faça mediações similares para a construção do triângulo acutângulo, também sem mencionar, ainda, essa nomenclatura.
Atividade principal
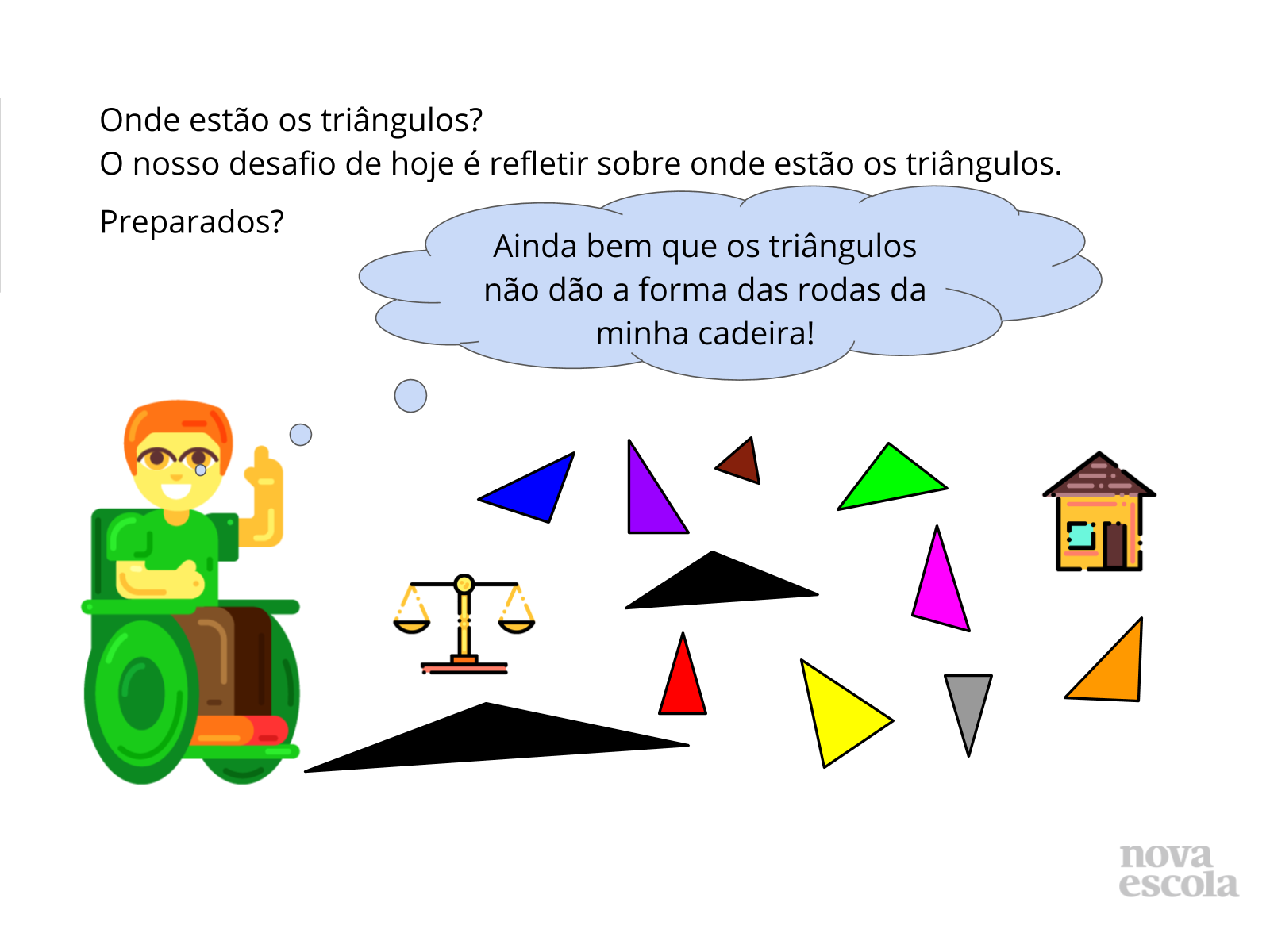
Tempo sugerido: 12 minutos.( slides de 4 a 7)
Orientações:
- Faça uma mediação que provoque reflexões acerca de como a imagem dos triângulos está presente em nosso contexto sociocultural, e que eles não são do mesmo tipo, em todas as situações, e que a escolha tem muito a ver com as medidas de seus ângulos.
- Sugira que reflitam mais sobre o assunto fazendo a Atividade Complementar 2.
Observação: Caso você ache pertinente, as atividades complementares podem ser utilizadas em sala de aula.
Propósito: Provocar reflexões acerca da presença e importância dos triângulos, em situações diversas;
Discuta com a turma: Para ver questões provocativas, confira o Guia de Intervenções.
Materiais Complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade Principal
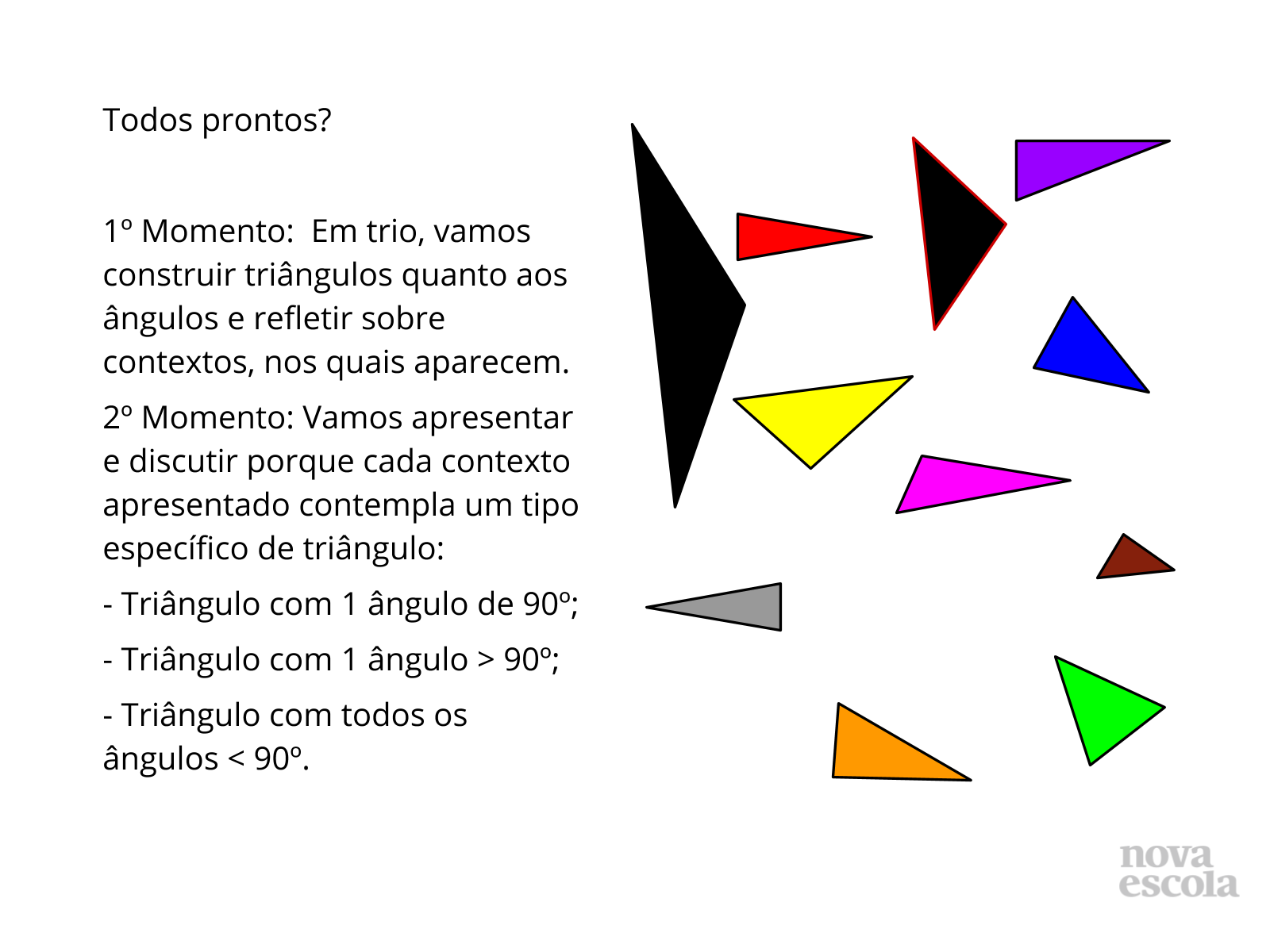
Tempo sugerido: 12 minutos.( slides de 4 a 7)
Orientações:
- Aqui, os estudantes têm uma ideia geral de como vai ocorrer a Atividade Principal, que se desenvolverá em 2 momentos.
- Atente às orientações específicas para cada um dos 2 momentos, nos slides posteriores, que serão apresentados aos estudantes. Informe à turma que a atividade será desenvolvida em 2 momentos.
Propósito: Apresentar uma ideia geral de como vai ocorrer a Atividade Principal.
1º Momento da Atividade Principal

Tempo sugerido: 12 minutos.( slides de 4 a 7)
Orientações:
- Arrume a sala em trios e solicite que todos peguem os materiais solicitados: cola, lápis (basta desenhar, não é preciso colorir, para que fique bem destacado o tipo de triângulo) e borracha.
- Distribua uma folha de papel A4 em branco para cada estudante fazer seu desenho.
- Distribua, também, 1 quadrado de papel para cada estudante. Confeccione-o, previamente, com 8 a 10 cm de lado e utilize qualquer papel de cor, para que se destaquem no desenho.
- Solicite que façam a atividade, individualmente, mas permita que haja colaboração entre os membros do trio, caso a colaboração seja requerida por quaisquer dos membros. Instrua para que o ângulo, se reto, tenha mesmo 90º.
- Vá em cada grupo e verifique se todos construíram e recortaram seus triângulos. Nesse passeio pelos grupos, aproxime-se dos que apresentam dificuldade para realizar a atividade, fazendo questões sobre a importância dos ângulos no triângulo, à medida que os estudantes forem trazendo ideias das imagens de triângulo que percebem em seus contextos.
Propósito: Construção de triângulos e utilização dos triângulos construídos em desenho, individual e colaborativamente
Discuta com o trio: Durante sua abordagem, sempre que perceber dificuldades para conceber o seu tipo de triângulo, faça questionamentos provocativos. Verifique algumas questões que podem ser colocadas durante sua abordagem:
- Qual é o seu triângulo? Por quê?
- Você pode me dar um exemplo de alguma situação, na qual lhe apareça a imagem desse tipo de triângulo?
- Será que há algum motivo especial para usar, por exemplo, este triângulo com 1 ângulo obtuso e não aquele com todos os ângulos agudos?
Observação: Obviamente, a questão provocativa vai depender da(s) dificuldade(s) apresentada(s). Atente para nunca dar uma resposta pronta ou antecipar a nomenclatura de classificação, ainda neste momento.
2º Momento da Atividade Principal -

Tempo sugerido: 12 minutos.( slides de 4 a 7)
Orientações:
- Arrume a sala, com a ajuda dos estudantes, colocando as carteiras em semicírculo.
- Convide, inicialmente, um dos grupos para ir ao espaço destinado à apresentação, pedindo-lhes que segurem seus desenhos, expondo-os para a visualização de todos.
- Convide um estudante para explicar por que aquele tipo de triângulo é o mais adequado àquela situação. Aproveite para informar que, em seguida, todos terão um tempo, em seguida, para discutir sobre as soluções apresentadas nos desenhos.
- Faça questões provocativas, buscando explicação mais aprofundada e focada no argumento do tipo de triângulo, conforme medida de ângulos, permitindo, no entanto, que os argumentos sobre as suas percepções da imagem daquele tipo de triângulo, no contexto escolhido, contemplem as seus interesses pessoais, vivenciais, sejam argumentos de caráter estético, utilitário, funcional, de necessidade, etc.
- Durante sua abordagem, sempre que perceber dificuldades ou equívocos conceituais, faça questionamentos provocativos, similares aos sugeridos no Discuta com a turma do slide anterior.
- Mais uma vez, a questão provocativa vai depender da(s) dificuldade(s) apresentada(s). Atente para nunca dar uma resposta pronta ou antecipar a nomenclatura correta, ainda neste momento.
Propósito: Apresentar os desenhos com tipos de triângulos, conforme medida de ângulos.
Discussão da solução

Tempo sugerido: 8 minutos.
Orientações:
- Peça, inicialmente, para que todos se sentem nas carteiras, buscando fechar uma circunferência com elas.
- Peça para 1 ou 2 estudantes ajudarem você na distribuição dos desenhos, no chão, no espaço central e visível a todos.
- Proponha que um dos estudantes inicie a discussão, a partir do seu desenho ou da observação do desenho de algum colega, que lhe despertou a atenção.
- Busque valorizar acertos e erros conceituais, partindo deles para provocar reflexões mais profundas sobre o assunto. Reforce os aspectos conceituais da classificação dos triângulos quanto aos ângulos, utilizando a nomenclatura correta.
- Busque sempre dar ou complementar uma conclusão, focando os ângulos dos triângulos nos contextos.
- Vá ao Guia de Intervenções e inspire-se ou aproveite algumas questões provocadoras, se forem necessárias para uma abordagem mais direta.
Propósito: Fazer contracenar situações pensadas pelos estudantes e os seus argumentos sobre a pertinência dos tipos de triângulos a elas.
Material Complementar:
Resolução da Atividade Principal
Sistematização do conceito
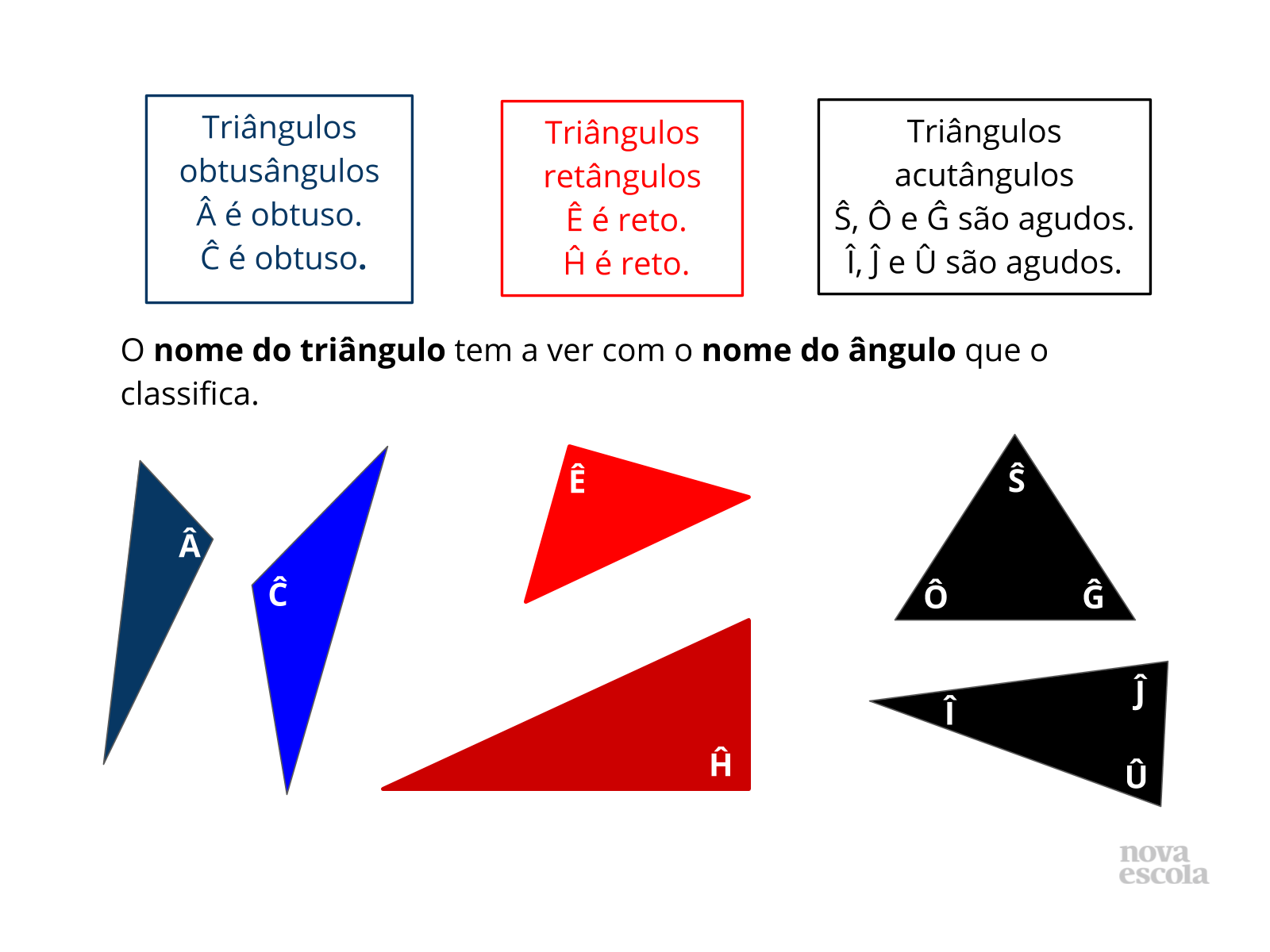
Tempo sugerido: 4 minutos.( slides 9 e 10)
Orientações:
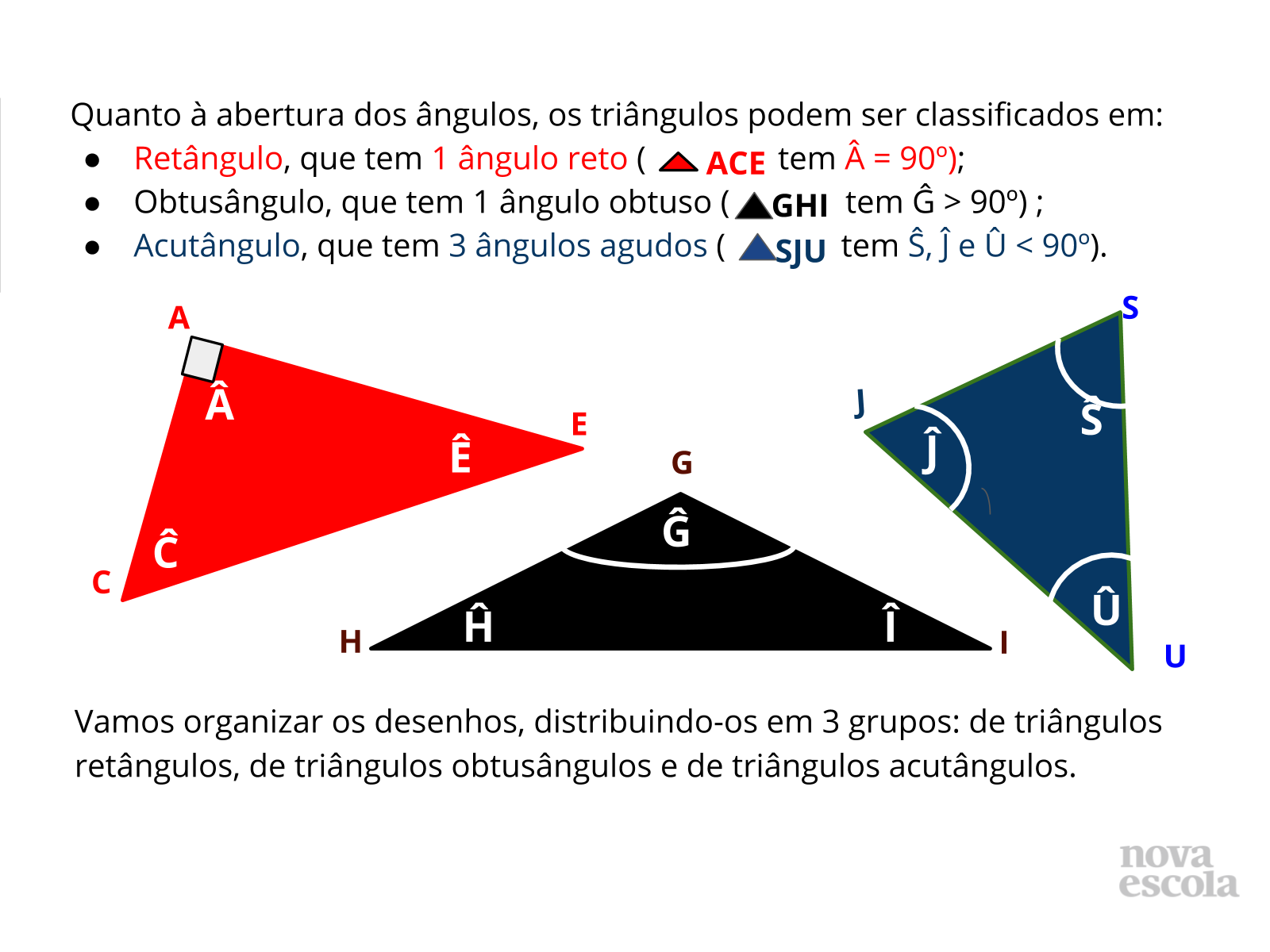
- Reforce os aspectos conceituais da classificação dos triângulos quanto aos ângulos, utilizando sempre a nomenclatura correta.
- Sinalize o(s) ângulo(s) que caracteriza(m) cada tipo de triângulo.
- Tente garantir que não é a posição, nem a área (não entre nesse conceito agora), mas é a medida dos ângulos o que importa na classificação quanto aos ângulos.
Propósito: Sistematizar a classificação dos triângulos quanto aos ângulos, ilustrando os aspectos-chave desta classificação.
Sistematização poética do conceito
Tempo sugerido: 4 minutos.( slides 9 e 10)
Orientações:
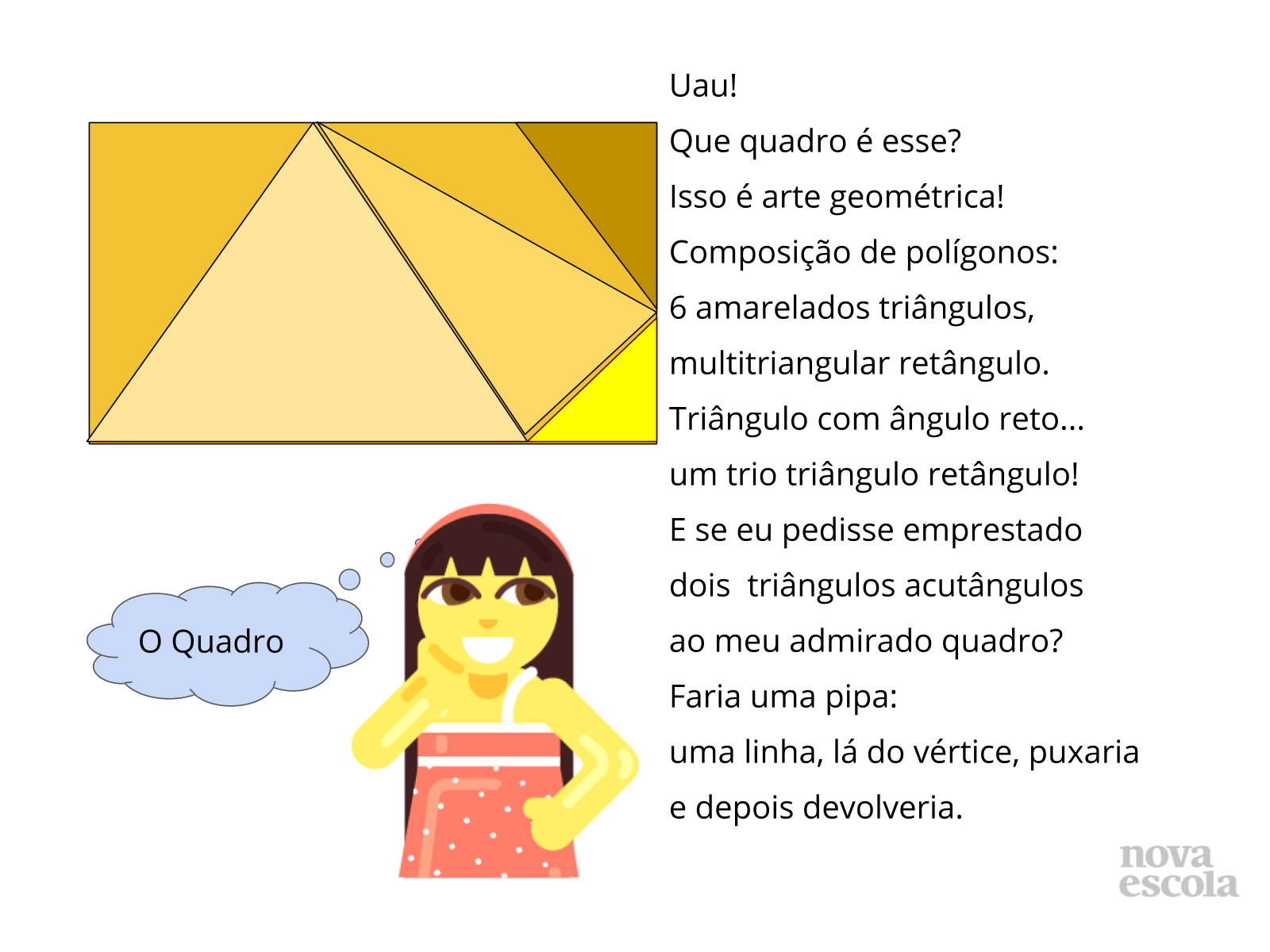
- Leia para todos o poema, enquanto os estudantes fruem da composição e da poesia lida.
- Informe-lhes que, depois, podem copiar o poema, se desejarem.
- Confira a Atividade complementar 3 pode ser acessada nos materiais complementares.
Observação: Caso você ache pertinente use as atividades complementares em sala de aula.
Propósito: Ilustrar que os conceitos e a linguagem matemática são importantes à leitura de mundo, à arte.
Encerramento
Tempo sugerido: 4 minutos.
Orientações:
- Não exceda mais de 2 minutos para apresentar a síntese do assunto e faça a proposta da organização, usando mais 2 minutos.
- Defina, previamente, o local para organizar os desenhos em pilhas, como a carteira do professor, uma prateleira do armário.
- No local predefinido, coloque sinalizador com o tipo de triângulo (retângulo, acutângulo e obtusângulo).
- A ideia é convidar os estudantes para ajudá-lo a guardar os desenhos já organizados, respeitando a classificação dos triângulos que lhe são pertinentes, quanto aos ângulos.
Que tal?! Certamente, as obras de arte dos pequenos artistas/matemáticos devem ficar muito boas, com os triângulos bem definidos e classificados conforme seus ângulos. Que tal juntar todos os desenhos já organizados e preparar um livrinho para servir de consulta a todos, por exemplo, na biblioteca da escola? Se você apoiar essa ideia, comunique-a aos estudantes, ou, alternativamente, faça-lhes uma surpresa, trazendo o livro na próxima aula. Utilize recursos simples para o livro, como um classificador com prendedores ou apenas os papéis grampeados com uma capinha, mas não se esqueça de colocar o título do livro, ano e turma de autores (se possível até uma folha impressa com os seus nomes) e o seu nome.
Propósito: Reunir os aspectos conceituais envolvidos na aula, destacando, de modo ilustrativo, os pontos-chave dos mesmos.
Raio X

Tempo sugerido: 10 minutos.( slides de 12 a 14)
Orientações:
- Imprima previamente a atividade para que seja realizada individualmente.
- Sem muito rigor na organização da sala, peça aos estudantes para se afastarem ou se arrumarem separadamente, porque vão fazer uma atividade que exigirá deles reflexão, atenção e conhecimento dos tipos de triângulos, quanto à abertura dos ângulos.
- Solicite que peguem régua, lápis, borracha e prestem atenção, deixando este slide exposto, para orientar sua fala.
- Descreva a proposta apresentada, por exemplo: temos 3 triângulos, de tamanhos e posições diferentes: a embarcação é um triângulo vermelho, com um ângulo maior que 90º, obtuso; a vela branca é um triângulo, que tem um dos seus vértices, o que tem um ângulo reto, de 90º, tocando a embarcação; e o leme azul é um triângulo com todos os seus ângulos são menores que 90º.
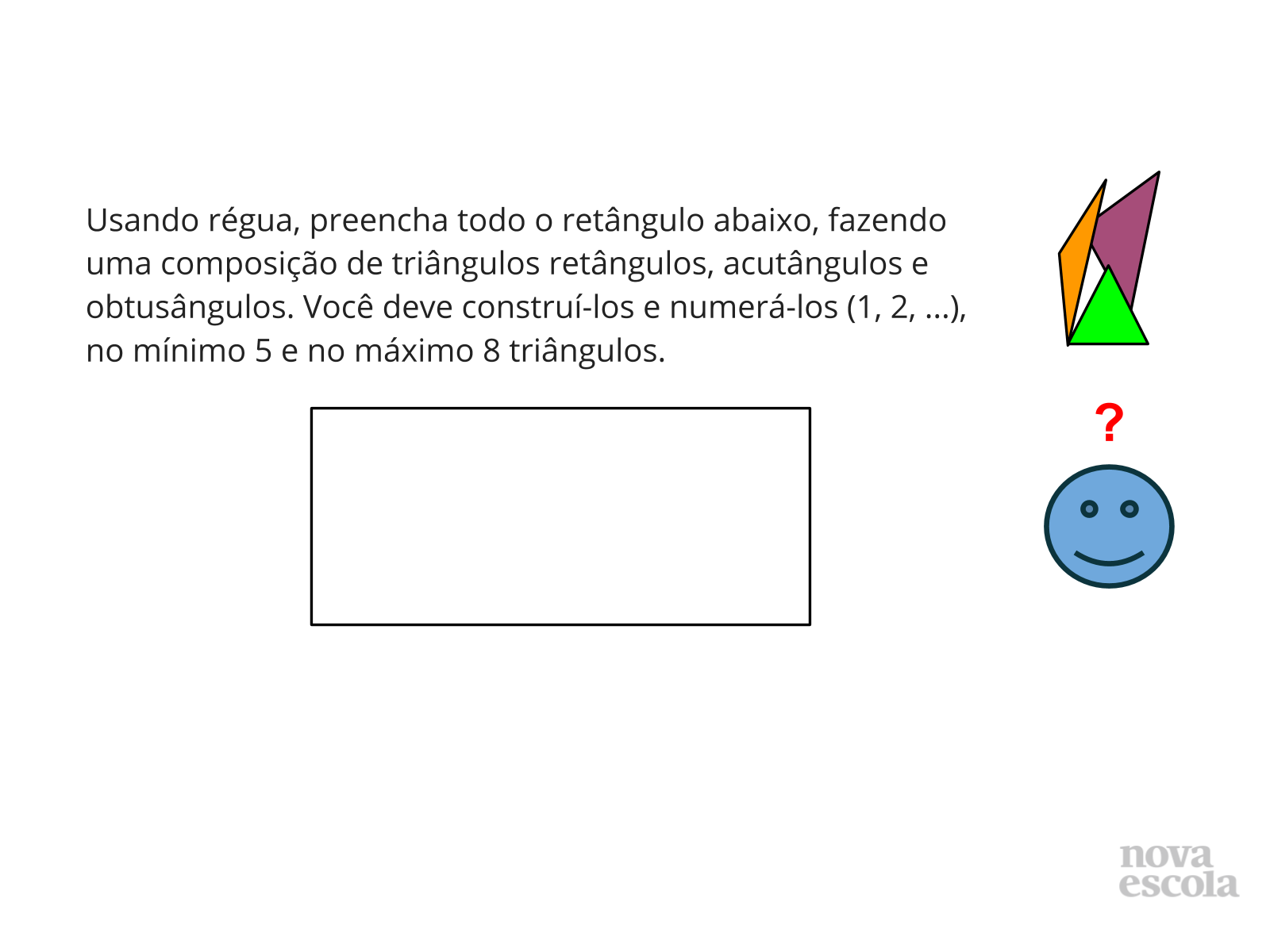
- Após discutir com a turma sobre o slide (ver abaixo), distribua a atividade e dê 8 minutos para responderem, orientando-os para: destinarem, no máximo, 3 minutos para a composição; numeração dos triângulos que construirão.
- Informe-os que podem utilizar dobraduras no retângulo de papel como alternativas para refletirem e responderem o que é solicitado.
- Se for solicitado, atenda à solicitação sem fazê-los passivos do conhecimento, mas provocando o seu esforço para tornar-se ativo naquele processo de construção de conhecimentos novos.
- Exceda esse tempo até o fim da aula.
- Verifique algumas intervenções para possíveis dificuldades e erros dos estudantes, acessando o Guia de Intervenção.
Propósito: Sensibilizar para a avaliação, na qual a composição de triângulos é requerida; também, à percepção de que os tipos de triângulos têm um sentido, além do matemático conceitual.
Discuta com a turma: No momento de apresentação do Slide, retome, breve e coletivamente, as características principais dos triângulos, em sua classificação quanto à abertura dos ângulos, fazendo questões provocativas, que reforcem a referência ao ângulo reto; ou leia a atividade para eles.
- Quanto aos ângulos, como vocês classificariam o triângulo vermelho?
- E o branco? E o azul? Por quê?
Observação: Faça uma mediação das respostas espontâneas, sempre utilizando a correta nomenclatura.
Materiais Complementares:
Raio X
Resolução do Raio X
Atividade complementar
Resolução da Atividade Complementar
Raio X
Tempo sugerido: 10 minutos.( slides de 12 a 14)
Orientações:
- Você pode deixar essa exibição da atividade, enquanto os estudantes a desenvolvem.
Propósito:Avaliar a aprendizagem da aula.
Raio X

Tempo sugerido: 10 minutos.( slides de 12 a 14)
Orientações:
- Você pode deixar essa exibição da atividade, enquanto os estudantes a desenvolvem.
Propósito: Avaliar a aprendizagem da aula.