Atividade principal
Plano de Aula
Plano de aula: Retângulos com mesmo perímetro e diferentes áreas
Plano 2 de uma sequência de 10 planos. Veja todos os planos sobre Cálculo de área e perímetro em quadrados e retângulos
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Samara Cintia Pinho de Moraes
Mentor: Fábio Menezes da Silva
Especialista de área: Fernando Barnabé
Habilidade da BNCC
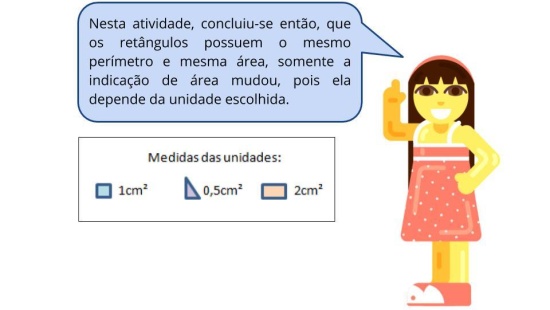
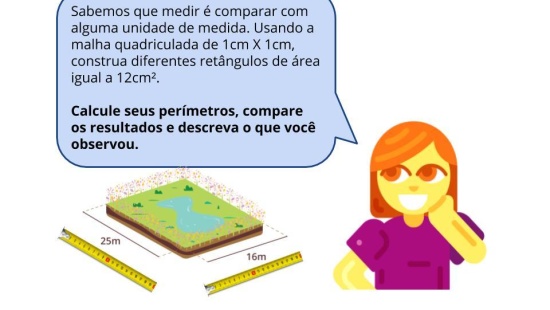
(EF05MA20) Concluir, por meio de investigações, que figuras de perímetros iguais podem ter áreas diferentes e que, também, figuras que têm a mesma área podem ter perímetros diferentes.
Objetivos específicos
- Conhecer medidas de superfície e seu contorno, sabendo diferenciá-las e comparar áreas por superposição e contagem de figuras planas pelos quadradinhos em malhas quadriculadas.
- Concluir, por meio de investigações, que figuras de perímetros iguais podem ter áreas diferentes e que, também, figuras que têm a mesma área podem ter perímetros diferentes.
Conceito-chave
Perímetro e área de figuras planas.
Recursos necessários
- Caderno,
- lápis,
- borracha,
- papel quadriculado,
- lápis de cor,
- papel sulfite para fotocópias.
Habilidades BNCC:
Objetivos de aprendizagem
- Conhecer medidas de superfície e seu contorno, sabendo diferenciá-las e comparar áreas por superposição e contagem de figuras planas pelos quadradinhos em malhas quadriculadas.
- Concluir, por meio de investigações, que figuras de perímetros iguais podem ter áreas diferentes e que, também, figuras que têm a mesma área podem ter perímetros diferentes.

Precisa de ajuda para criar uma aula personalizada?
Crie seu plano de aula em menos de um minuto no WhatsApp.