Resumo da aula
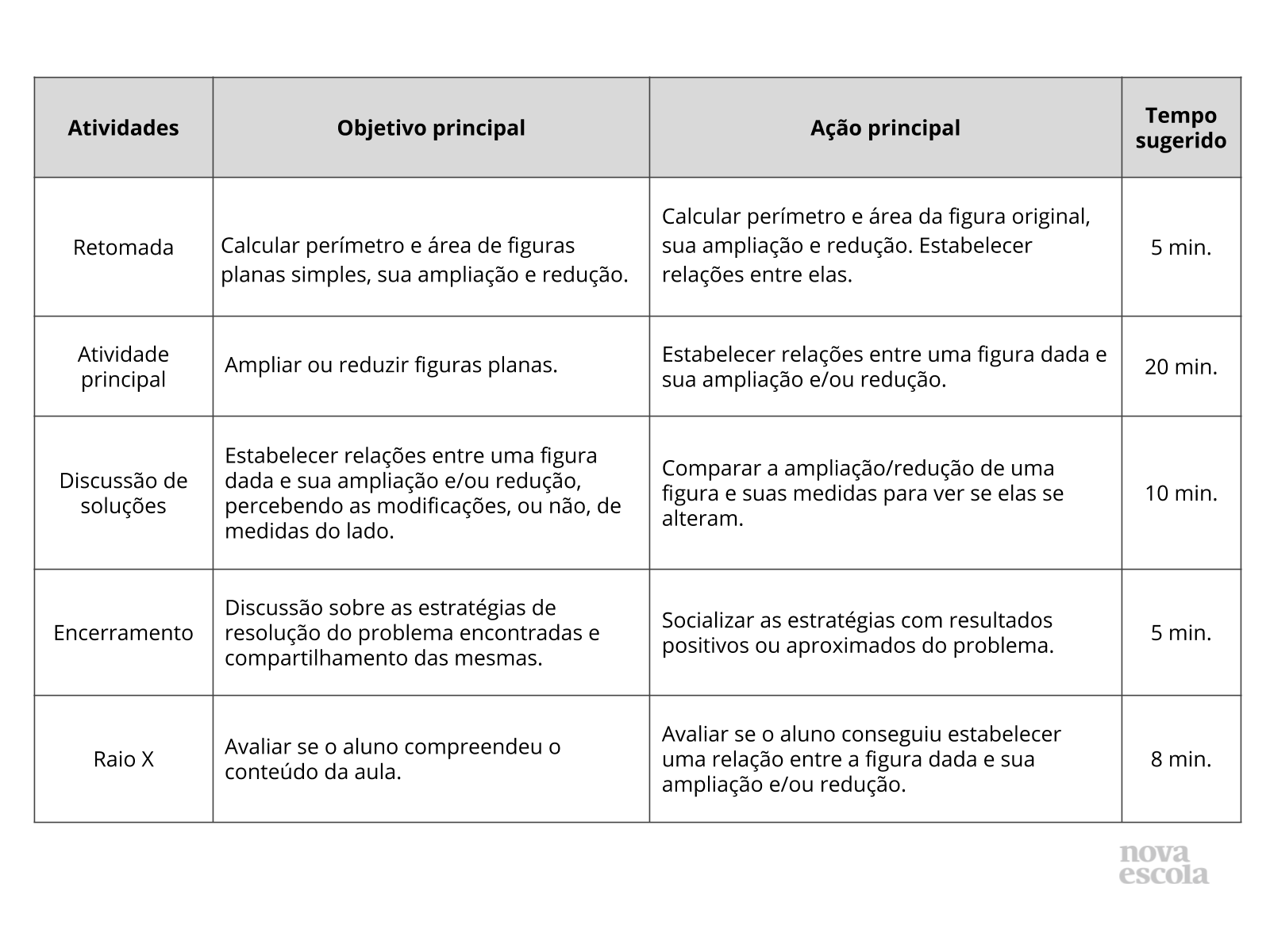
Esta tabela é um resumo da aula. Aqui estão elencados em ordem cronológica as etapas, objetivos e ações que deverão ser realizadas em cada uma delas.
Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações o nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar a proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça o download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Passar o objetivo na lousa e explicar sobre o que vão aprender na aula.
Propósito: O aluno saberá o que o professor espera que ele aprenda ao final da aula.
Retomada

Tempo sugerido: 5 min.
Orientação: Os alunos podem ser divididos em duplas, por níveis diferentes de conhecimento matemático e não por afinidade entre eles. Para que isso ocorra, sugerimos que se faça um diagnóstico da turma, mesmo para os alunos com necessidades especiais.
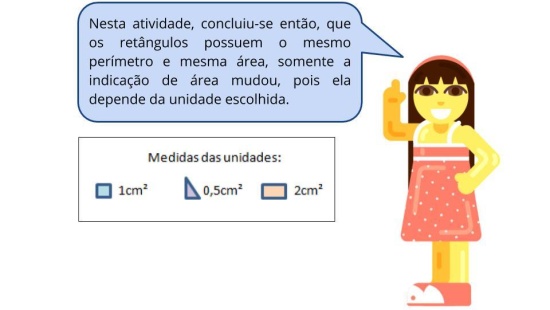
Partindo do conhecimento prévio dos alunos sobre os conceitos de perímetro e área, será trabalhado a ampliação e redução de figuras e formas plana. Por meio da explicação e exemplificação, espera-se levar os alunos a estabelecer relações entre o perímetro e a área da figura a ser ampliada e reduzida.
Propósito: Fazer com que o aluno estabeleça uma relação entre o perímetro e a área da figura original, reduzida e ampliada.
Discuta com a turma:
- Observando as três figuras, o que vocês podem dizer sobre elas?
- Vocês sabem que tipo de profissionais usam a ampliação e redução de imagens em seu trabalho?
Com essas perguntas, pode-se perceber o nível de percepção visual dos alunos em relação a proporção e o conhecimento sobre a utilidade social e profissional do que vão aprender sobre área e perímetro.
Retomada

Tempo sugerido: 2 min.
Atividade Principal

Tempo sugerido: 15 min.
Orientação: Nesta atividade, os alunos permanecerão no mesmo grupo. O professor deve fazer a leitura compartilhada do enunciado da atividade, para auxiliar no entendimento do que o texto informa e pede que se faça, principalmente para os alunos especiais e os com dificuldades de aprendizagem.
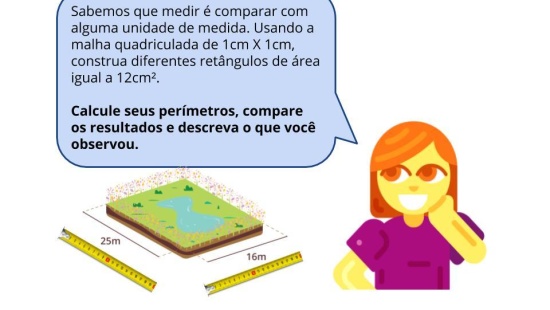
Para resolver a atividade, os alunos receberão um modelo da figura desenhada numa malha quadriculada de 2cm X 2cm. Será distribuído a cada um dos alunos da dupla uma folha de malha quadriculada de 1cm X 1cm e uma de 4cm X 4cm. Nesta malha, eles deverão reproduzir o desenho original, seguindo a mesma quantidade de quadradinhos utilizados neles.
Propósito: Estabelecer relações entre uma figura dada e sua ampliação e/ou redução.
- Como podemos copiar o desenho de forma que fique igual ao original?
- Há uma forma fácil de desenhar sem se atrapalhar com tantos quadradinhos?
Os alunos perceberão que há necessidade de contar os quadradinhos utilizados no desenho para então reproduzi-lo. Após os alunos desenharem e calcularem os perímetros e áreas, será mais fácil para que respondam às questões feitas anteriormente. Na comparação visual eles deverão perceber se os desenhos são semelhantes em forma ou se houve alguma deformação dela, se isso acontecer é porque o aluno usou quadradinhos a mais ou a menos. Já na comparação dos cálculos os alunos devem perceber que apesar da forma dos desenhos serem semelhantes, seus perímetros e áreas se modificaram em relação ao desenho original, diminuindo e aumentando as medidas.
Material complementar para impressão:
Atividade Principal
Guia de intervenção
Discussão da solução

Tempo sugerido: 15 minutos.
Orientações: Ao trabalhar a resolução da atividade é importante socializar as estratégias utilizadas pelos alunos para resolver a atividade. Solicitar que alguns alunos escrevam no quadro a forma como chegaram ao resultado, mesmo que seja uma forma diferente mostrada pelo professor ou por outro colega, pois é importante apresentar outras possibilidades de resolução. Esse procedimento facilita também apontar erros de percurso na estratégia do aluno, para que ele descubra onde errou e possa futuramente evitar o mesmo erro, assim como descobrir qual a dificuldade encontrada no processo de resolução ou não compreensão da proposta da atividade.
Propósito: Compartilhamento de ideias e estratégias na busca da resolução do problema; e percepção dos erros em suas estratégias a partir da comparação com a dos outros colegas.
Discuta com a turma:
- O que vocês perceberam ao comparar os desenhos que fizeram com o desenho original?
- O que foi mais difícil de fazer nessa atividade?
- Que estratégias vocês usaram?
- Ao comparar a medida do perímetro e da área dos 3 desenhos, o que vocês perceberam?
Material complementar para impressão:
Atividade Principal
Guia de intervenção
Discussão da solução

Tempo sugerido: 15 minutos.
Orientações: Ao trabalhar a resolução da atividade é importante socializar as estratégias utilizadas pelos alunos para resolver a atividade. Solicitar que alguns alunos escrevam no quadro a forma como chegaram ao resultado, mesmo que seja uma forma diferente mostrada pelo professor ou por outro colega, pois é importante apresentar outras possibilidades de resolução. Esse procedimento facilita também apontar erros de percurso na estratégia do aluno, para que ele descubra onde errou e possa futuramente evitar o mesmo erro, assim como descobrir qual a dificuldade encontrada no processo de resolução ou não compreensão da proposta da atividade.
Propósito: Compartilhamento de ideias e estratégias na busca da resolução do problema; e percepção dos erros em suas estratégias a partir da comparação com a dos outros colegas.
Discuta com a turma:
- O que vocês perceberam ao comparar os desenhos que fizeram com o desenho original?
- O que foi mais difícil de fazer nessa atividade?
- Que estratégias vocês usaram?
- Ao comparar a medida do perímetro e da área dos 3 desenhos, o que vocês perceberam?
Discussão da solução
Tempo sugerido: 15 minutos.
Orientações: Ao trabalhar a resolução da atividade é importante socializar as estratégias utilizadas pelos alunos para resolver a atividade. Solicitar que alguns alunos escrevam no quadro a forma como chegaram ao resultado, mesmo que seja uma forma diferente mostrada pelo professor ou por outro colega, pois é importante apresentar outras possibilidades de resolução. Esse procedimento facilita também apontar erros de percurso na estratégia do aluno, para que ele descubra onde errou e possa futuramente evitar o mesmo erro, assim como descobrir qual a dificuldade encontrada no processo de resolução ou não compreensão da proposta da atividade.
Propósito: Compartilhamento de ideias e estratégias na busca da resolução do problema; e percepção dos erros em suas estratégias a partir da comparação com a dos outros colegas.
Discuta com a turma:
- O que vocês perceberam ao comparar os desenhos que fizeram com o desenho original?
- O que foi mais difícil de fazer nessa atividade?
- Que estratégias vocês usaram?
- Ao comparar a medida do perímetro e da área dos 3 desenhos, o que vocês perceberam?
Encerramento

Tempo sugerido: 5 minutos.
Orientação: Fazer um apanhado geral sobre o que foi ensinado e aprendido na aula sobre perímetro e área.
Propósito: Pontuar os conceitos estudados em aula.
Raio x

Tempo sugerido: 8 minutos.
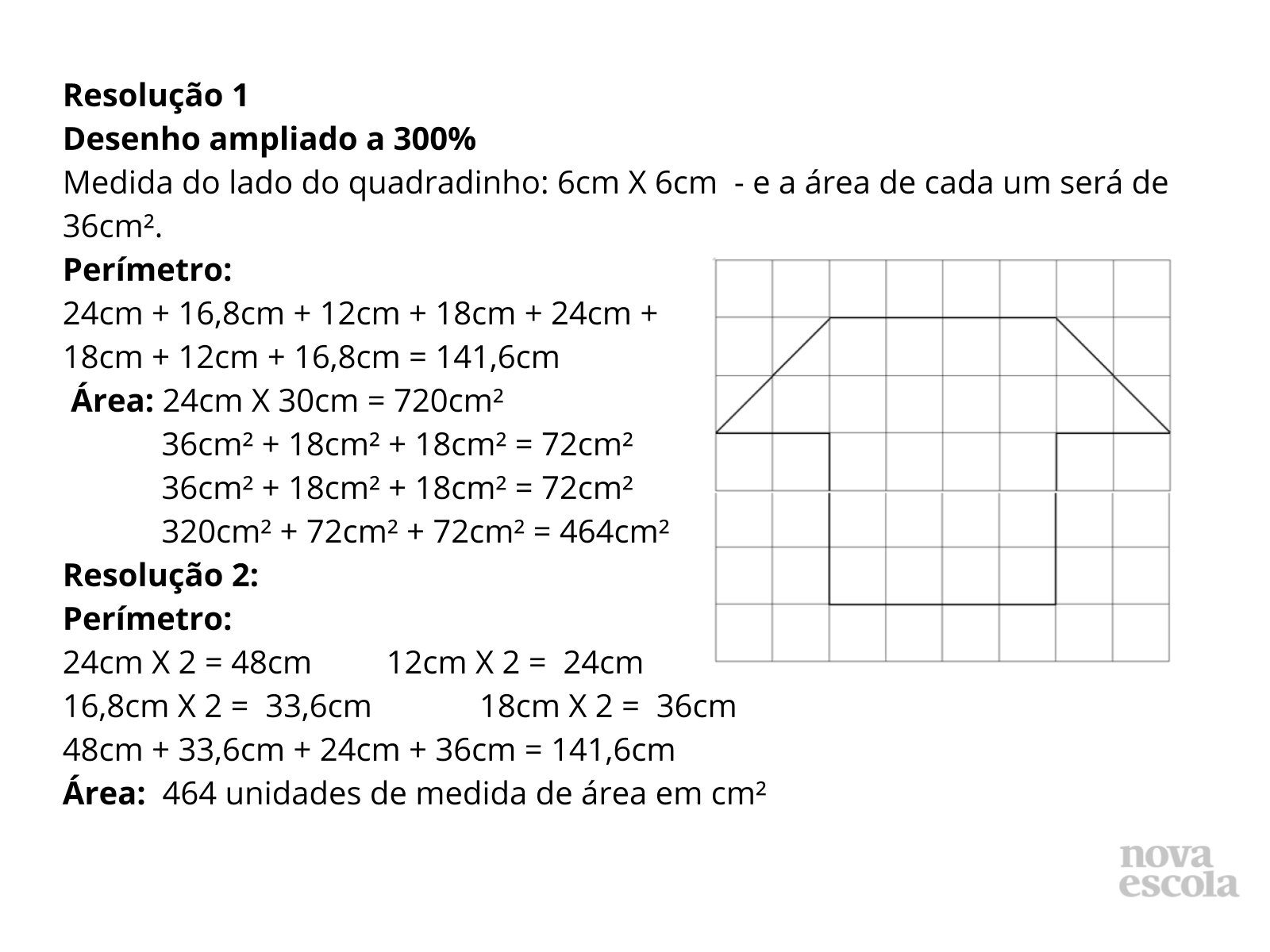
Orientações: Essa atividade tem o objetivo de avaliar se o aluno aprendeu o conteúdo dado, ou, se apresenta dificuldades de compreensão do mesmo. Ela é realizada individualmente, podendo ser usada em malha quadriculada ou fotocópia, disponível no modelo para impressão. Essa atividade apresenta um nível complexidade maior. Para acessar o resultado da atividade clique em Resolução do raio X .
Propósito: Verificar se os alunos ainda possuem dificuldade na apropriação dos conceitos e cálculos de perímetro e área, assim como se entenderam que ocorrem mudanças nas medidas dessas dua grandezas, mesmo as figuras sendo semelhantes.
Discuta com a turma:
- Quais dificuldades vocês tiveram para resolver essa atividade?
- Quais estratégias vocês usaram?
- Ao comparar as figuras o que puderam perceber?
Materiais complementares
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar