Aquecimento
Plano de Aula
Plano de aula: Jogo Do Desafio Na Reta Real
Plano 10 de uma sequência de 10 planos. Veja todos os planos sobre Ampliação dos campos numéricos: números reais
Descrição
Este plano de aula foi elaborado pelo Time de autores NOVA ESCOLA
Autora: Maria Bernadete Estradioto
Mentor: Fernando de Mello Trevisani
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNC
EF09MA01; EF09MA02 - Ampliação dos campos numéricos: números reais (a necessidade de medir qualquer segmento de reta: números irracionais e seu significado; representação na reta numerada).
Objetivos específicos
Localização de números reais na reta real e em intervalos.
Conceito-chave
Localizar números reais na reta real e em intervalos.
Recursos necessários
Projetor ou impresso das atividades.
Pré-conhecimento da turma
- Intervalos abertos, fechados e semi abertos.
- Intervalos ilimitados.
- Números racionais e irracionais.
Habilidades BNCC:
Objetivos de aprendizagem
Localização de números reais na reta real e em intervalos.
Resumo da aula
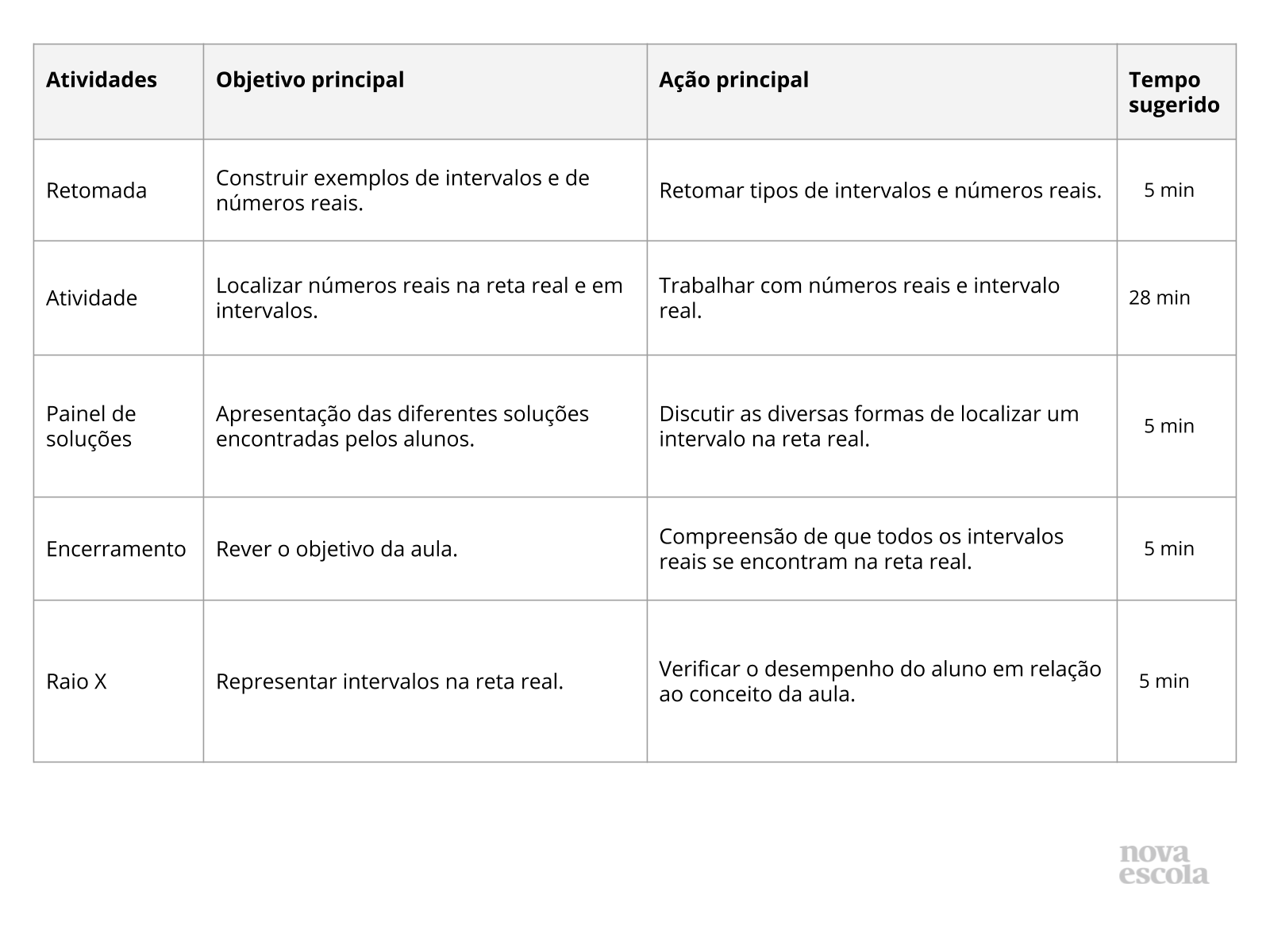
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Apresente o objetivo aos alunos.
Propósito: Apresentar o objetivo da aula e o que se espera dos alunos nessa aula.
Retomada

Tempo sugerido: 5 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem. Em seguida, deixe que discutam com um colega suas soluções. Reserve um tempo para um debate coletivo e deixe que as duplas compartilhem o que discutiram.
Propósito: Retomar os tipos de intervalos e números reais.
Discuta com a turma:
- Pergunte se ainda existem dúvidas em relação aos tipos de intervalos.
Materiais complementares para impressão:
Atividade principal
Tempo previsto: 28 minutos (slides 4 a 20)
Orientações: : Forme grupos de 5 alunos, oriente os grupos a se posicionarem de forma que a possibilidade de interação entre eles e também com você, professor, seja favorecida.
As cores são meramente ilustrativas.
Propósito: Dividir os alunos em grupos.
Materiais complementares para impressão:
Atividade principal
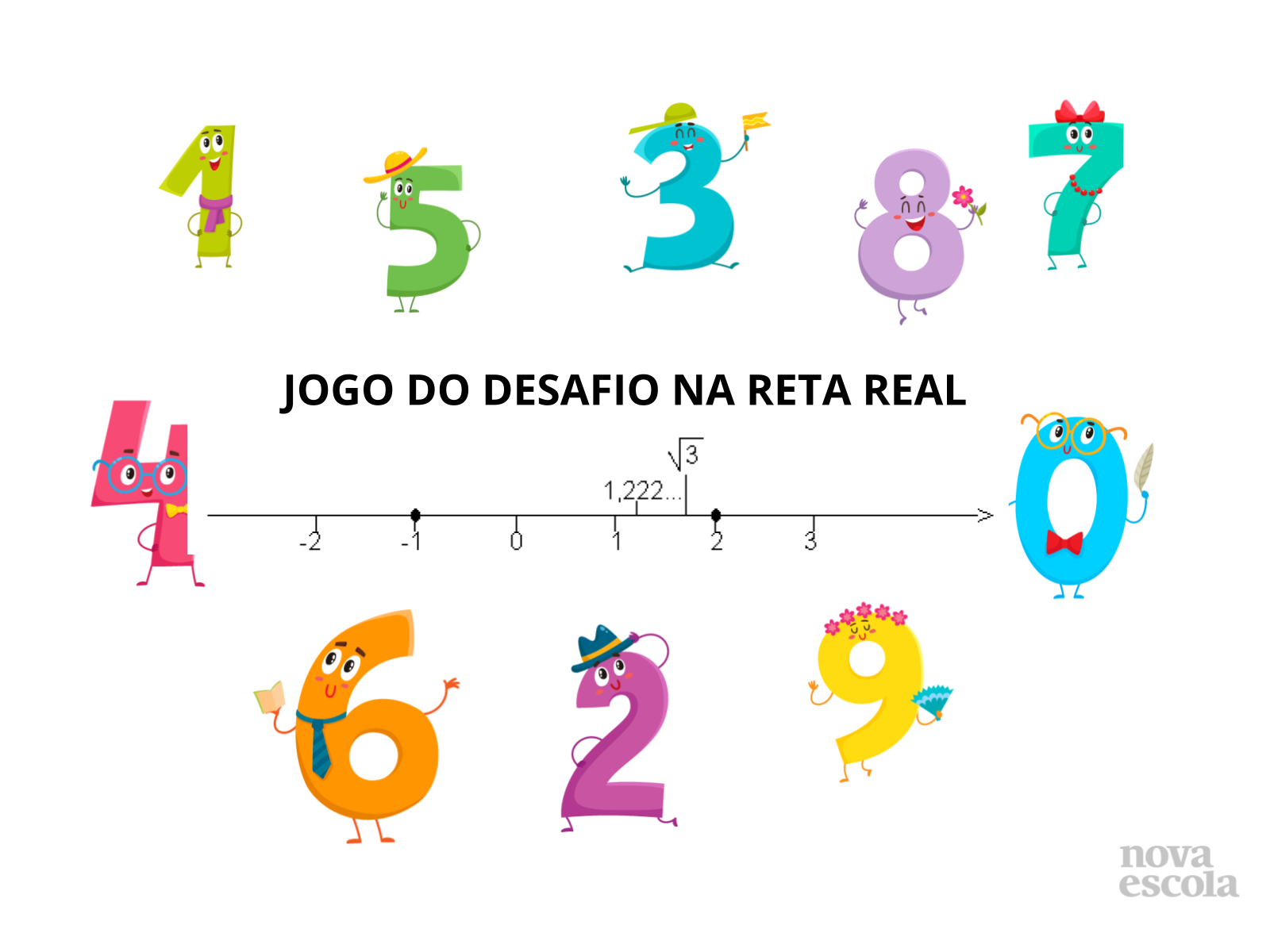
Tempo previsto: 28 minutos (slides 4 a 20)
Orientações: : Forme grupos de 5 alunos, oriente os grupos a se posicionarem de forma que a possibilidade de interação entre eles e também com você, professor, seja favorecida.
As cores são meramente ilustrativas.
Propósito: Dividir os alunos em grupos.
Atividade principal

Tempo previsto: 28 minutos (slides 4 a 20)
Orientação: Três equipes deverão responder, mas todas devem fazer a atividade. As equipes só vão saber quais serão as 3 que irão socializar as respostas após o tempo dado para que eles respondam. O professor irá dizer quais equipes são. Nos slides seguintes há duas tabelas, a colorida é uma sugestão para que conduza a sequência das respostas e a não colorida é uma sugestão para marcar os pontos. É possível imprimir para que os alunos possam visualizar e acompanhar a marcação dos pontos.
Propósito: Os alunos conhecerem as regras do jogo.
Discuta com a turma:
- Converse sobre as regras do jogo. Garantir que todos entenderam as regras.
Atividade principal
Tempo previsto: 28 minutos (slides 4 a 20)
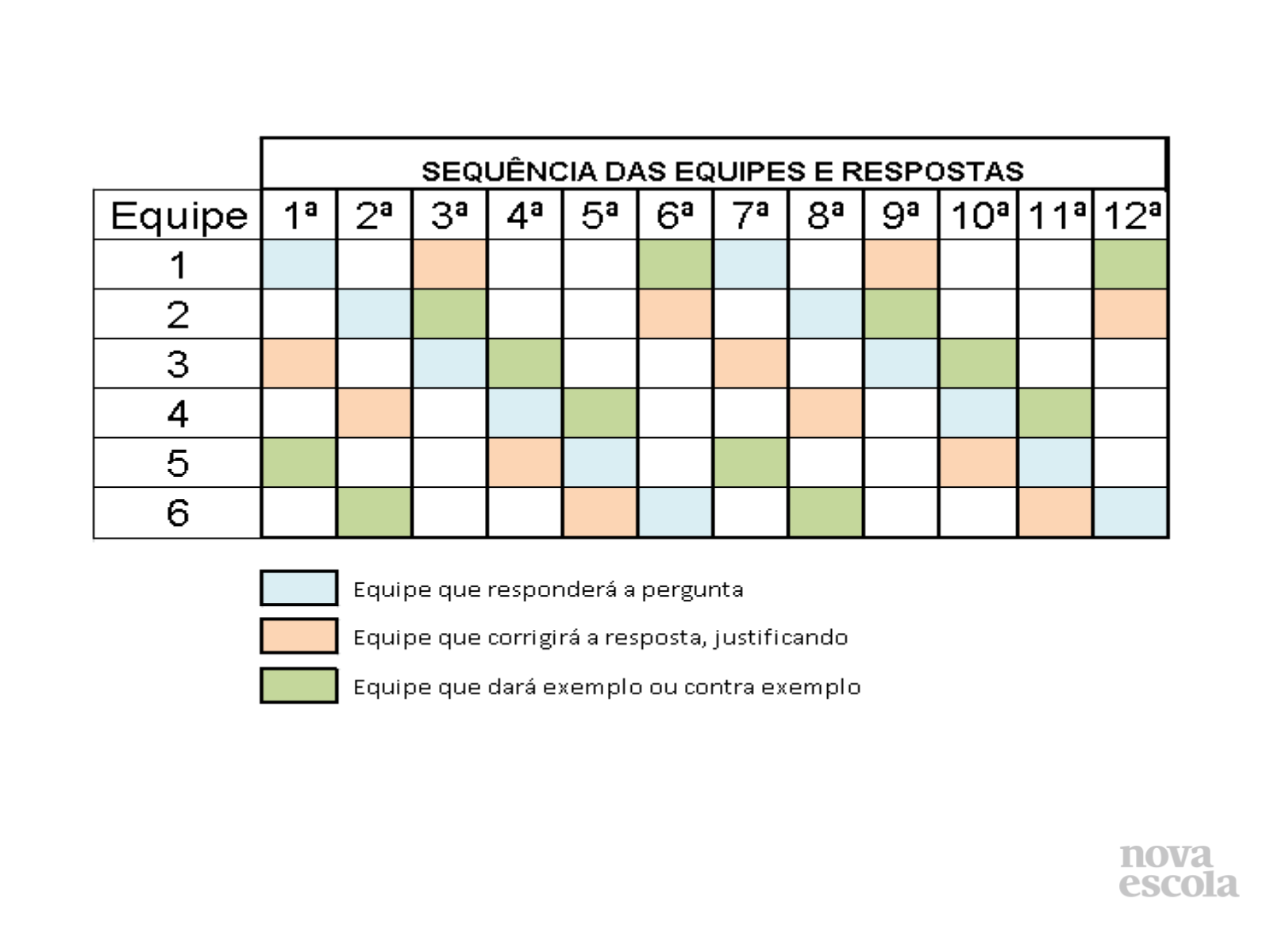
Orientação: Tabela da sequência das equipes e respostas. Três equipes deverão responder, mas todas devem fazer a atividade.
Propósito: Os alunos conhecerem as regras do jogo.
Discuta com a turma:
- Converse sobre a tabela, garantir que todos entenderam.
Atividade principal

Tempo previsto: 28 minutos (slides 4 a 20)
Orientação: A tabela pode ser usada para marcar os pontos ganho em cada rodada.
Pode imprimir uma tabela para cada equipe, esta tabela para impressão se encontra no arquivo da Atividade de aula.
Propósito: Sugestão de tabela para marcação dos pontos.
Discuta com a turma:
- Converse sobre a tabela, garantir que todos entenderam.
Atividade principal

Tempo previsto: 28 minutos (slides 4 a 20)
Orientação:
- A equipe 1 deverá responder que 0,3 é um número racional, portanto pode ser escrito em forma de fração e é possível localizá-lo com precisão no intervalo dado.
- A equipe 3 deverá corrigir a resposta confirmando que 0,3 pode ser escrito em forma de fração e está dentro do intervalo.
- A equipe 5 deverá argumentar que 0 < 0,3 < +?
Propósito: Entender que números racionais fazem parte da reta real e podem ser localizados dentro de um intervalo com precisão.
Discuta com a turma:
- Pergunte se todos os números racionais podem ser escritos em forma de fração.
- Pergunte se é possível formar um intervalo com o conjunto dos números racionais.
- Pergunte se é possível formar um intervalo somente com o conjunto dos números racionais.
Atividade principal

Tempo previsto: 28 minutos (slides 4 a 20)
Orientação:
- A equipe 2 deverá responder que 0,312576539… é um número irracional, portanto não pode ser escrito em forma de fração e é possível localizar em um intervalo entre dois números inteiros.
- A equipe 4 deverá corrigir a resposta confirmando que é um número irracional e pode ser localizado entre dois números inteiros.
- A equipe 6 deverá argumentar: o intervalo formado por dois números inteiros onde 0,312576539… se encontra, é o intervalo entre 0 e 1.
Propósito: Entender que números irracionais fazem parte da reta real e podem ser localizados dentro de um intervalo entre dois números inteiros.
Discuta com a turma:
- Pergunte se é possível formar um intervalo com o conjunto dos números irracionais.
- Pergunte se é possível formar um intervalo somente com o conjunto dos números irracionais.
Atividade principal

Tempo previsto: 28 minutos (slides 4 a 20)
Orientação:
- A equipe 3 deverá responder que intervalo semi-fechado é aquele em que um dos extremos faz parte do intervalo.
- A equipe 1 deverá confirmar a resposta acima.
- A equipe 2 deverá dar um exemplo de intervalo semi-fechado : ] a , b ] ou [ a , b [
Propósito: Entender que intervalo fechado é aquele onde um dos extremos faz parte do intervalo.
Discuta com a turma:
- Pergunte se é possível formar um intervalo semi-fechado em que os dois extremos fazem parte do intervalo.
- Pergunte se é possível formar um intervalo semi-fechado em que os dois extremos não fazem parte do intervalo.
Atividade principal

Tempo previsto: 28 minutos (slides 4 a 20)
Orientação:
- A equipe 4 deverá responder que há infinitos números entre dois inteiros sucessivos e que podemos localizar todos na reta real.
- A equipe 5 deverá corrigir a resposta confirmando a resposta acima.
- A equipe 3 deverá dar um exemplo de números localizados entre dois inteiros sucessivos, como 3,5 entre 3 e 4.
Propósito: Compreender que todos os números são possíveis de localizar na reta real.
Atividade principal

Tempo previsto: 28 minutos (slides 4 a 20)
Orientação:
- A equipe 5 deverá responder que, quando o extremo é infinito, não pode ser localizado como ponto.
- A equipe 6 deverá confirmar a afirmação acima.
- A equipe 4 deverá dar um exemplo : ] -? , b] ; [ a , +? [ ou ] -? , +? [
Propósito: Compreender que infinito na reta real é uma indicação de infinitos números e não um ponto.
Discuta com a turma:
- O que é infinito na reta real?
- O que é um ponto na reta real?
Atividade principal

Tempo previsto: 28 minutos (slides 4 a 20)
Orientação:
- A equipe 6 deverá responder que é um intervalo ilimitado, tendo “a” como origem.
- A equipe 2 deverá confirmar a resposta acima.
- A equipe 1 deve dar um exemplo de intervalo ilimitado.
Propósito: Reconhecer através de notação um intervalo ilimitado.
Discuta com a turma:
- Como podemos reconhecer o tipo de um intervalo, observando a notação?
- “a” pertence ao intervalo?
Atividade principal

Tempo previsto: 28 minutos (slides 4 a 20)
Orientação:
- A equipe 1 deverá responder que podemos localizar todos os números que formam o intervalo na reta real.
- A equipe 3 deverá confirmar a resposta acima.
- A equipe 5 deverá dar um exemplo a critério da equipe.
Propósito: Reconhecer que todos os números do intervalo estão na reta real.
Discuta com a turma:
- Quais números do intervalo não podemos localizar na reta real?
- Existe algum intervalo que não podemos localizar na reta real?
Atividade principal

Tempo previsto: 28 minutos (slides 4 a 20)
Orientação:
- A equipe 2 deverá responder que independente do tipo de intervalo, um número irracional sempre poderá ser localizado na reta real, sem precisão.
- A equipe 4 deverá confirmar a resposta acima.
- A equipe 6 deverá dar um exemplo a critério da equipe.
Propósito: Perceber que um número irracional, independente de estar ou não em um intervalo, pode ser localizado na reta real, mas sem precisão.
Discuta com a turma:
- Existe algum número irracional que podemos localizar com precisão na reta real?
- Existe algum tipo de intervalo em que seja possível localizar um número irracional na reta real?
Atividade principal

Tempo previsto: 28 minutos (slides 4 a 20)
Orientação:
- A equipe 3 deverá responder que o intervalo em questão não é formado apenas por alguns números, mas infinitos números, além do que o -3 não faz parte deste intervalo, pois é aberto no -3, e que o 0 faz parte deste intervalo, pois é fechado no 0.
- A equipe 1 deverá confirmar a resposta acima.
- A equipe 2 deverá dar exemplo de alguns números que formam este intervalo.
Propósito: Perceber que dentro de um intervalo há infinitos números reais.
Discuta com a turma:
- Quem são os extremos deste intervalo?
- Quais extremos fazem parte deste intervalo?
Atividade principal

Tempo previsto: 28 minutos (slides 4 a 20)
Orientação:
- A equipe 4 deverá responder que intervalo ilimitado é aquele onde um dos extremos é infinito, não tendo limite de início e fim.
- A equipe 5 deverá confirmar a resposta acima.
- A equipe 3 deverá dar um exemplo de intervalo onde os dois extremos ou apenas um deles é infinito.
Propósito: Compreender que quando um dos extremos é infinito, o intervalo não tem limite.
Discuta com a turma:
- O que define o limite do intervalo? (onde começa e onde termina).
- O infinito não define o limite do intervalo? (Não, pois se o intervalo vai para o infinito é ilimitado).
Atividade principal

Tempo previsto: 28 minutos (slides 4 a 20)
Orientação:
- A equipe 5 deverá responder que sim, um intervalo ilimitado nos dois extremos contém todos os números naturais, porém é impossível um intervalo somente com os números naturais.
- A equipe 6 deverá confirmar a resposta acima.
- A equipe 4 deverá dar o seguinte exemplo : ] -? , +? [
Propósito: Compreender que não é possível a existência de um intervalo apenas com números naturais.
Discuta com a turma:
- Existe um intervalo somente com números racionais? (Não)
- Existe um intervalo somente com números irracionais? (Não)
- Existe um intervalo somente com números racionais e irracionais? (Sim, pois os dois conjuntos contemplam todos os números da reta real.
Atividade principal

Tempo previsto: 28 minutos (slides 4 a 20)
Orientação:
- A equipe 6 deverá responder que é possível que em um intervalo se encontre raiz de 16 e de cinco, porém impossível um intervalo apenas com esses dois números.
- A equipe 2 deverá confirmar a resposta acima.
- A equipe 1 deverá dar um exemplo de intervalo que inclua as duas raízes.
Propósito: Compreender que não é possível formar um intervalo somente com as duas raízes, mas é possível um intervalo onde as duas raízes se encontram.
Discuta com a turma:
- Se as duas raízes fazem parte do intervalo, posso formar um intervalo em que as duas raízes sejam extremos e o tipo de intervalo seja aberto?
Discussão de soluções
Tempo sugerido: 5 minutos
Orientação: Momento de socializar o aprendizado da aula, pedir aos alunos que falem sobre o que aprenderam, e as dúvidas que ainda existem sobre localização de números reais na reta real e em intervalos.
Se achar que ainda há tempo hábil para mais uma atividade, a sugestão é que use a Atividade Complementar.
Discuta com a turma:
- Oriente sobre as dificuldades a partir da fala dos alunos.
- Use o guia de intervenção para auxiliar nas dúvidas mais frequentes.
Encerramento
Tempo sugerido: 5 minutos
Orientação: Momento de rever o objetivo da aula, saliente que todos os números reais podem ser localizados na reta real, seja individualmente ou dentro de intervalos.
Propósito: Compreender que todos os números podem ser representados na reta real, mesmo que estes números façam parte de um intervalo..
Discuta com a turma:
Faça perguntas como:
- Um número real dentro de um intervalo faz parte da reta real?
- Os limites de um intervalo significam que os extremos fazem parte do intervalo?
Raio X
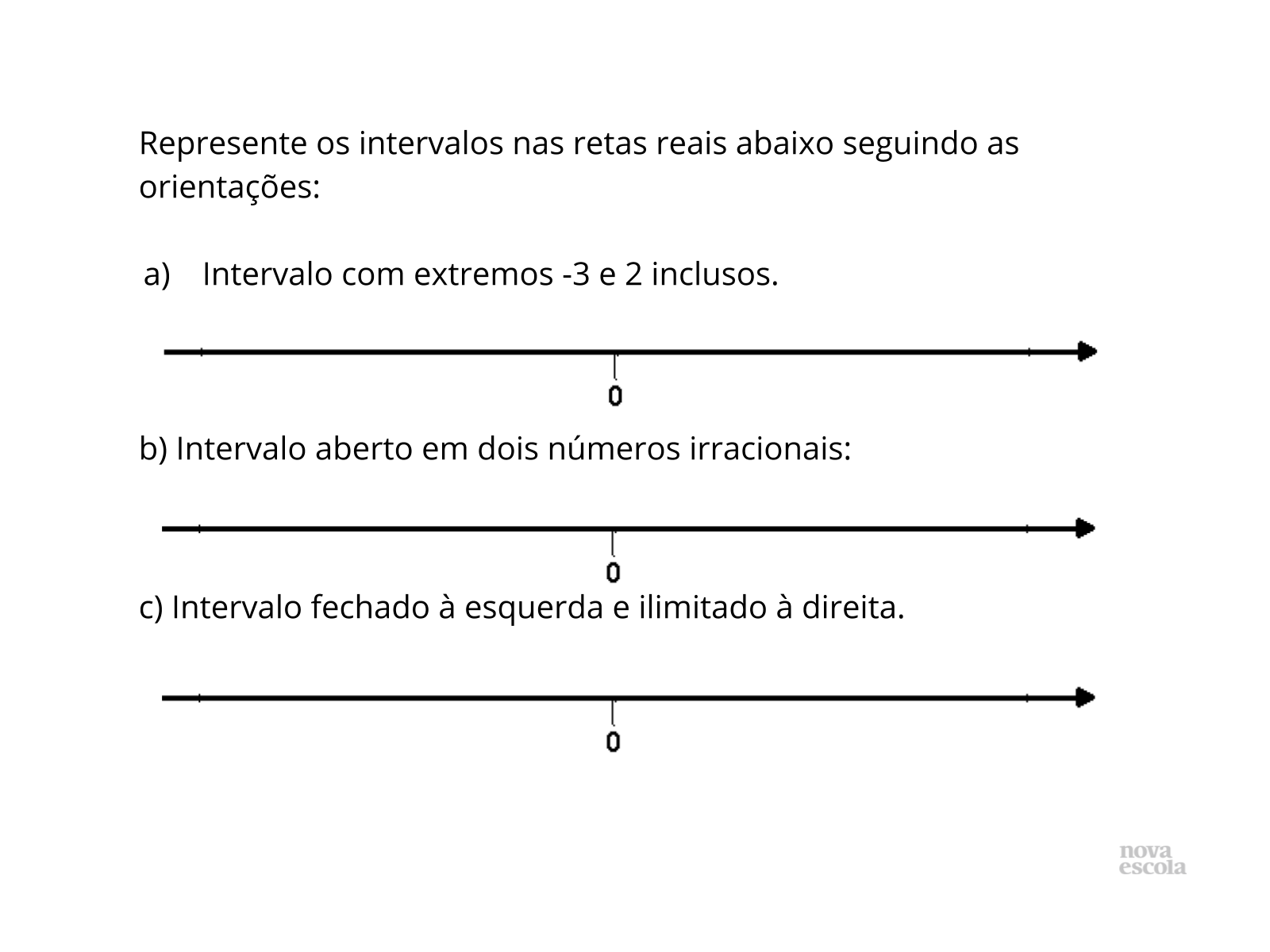
Tempo sugerido: 5 minutos
Orientação: Utilize o Guia de Intervenção para discutir com os alunos as dúvidas mais frequentes.
Propósito: Representar intervalos na reta real.
Discuta com a turma:
- Pergunte se há dúvidas em localizar números reais na reta real e em intervalos.
Materiais complementares para impressão:
Sugestão de adaptação para ensino remoto
Ferramentas sugeridas
- Essenciais: alguma rede social: Whatsapp, Facebook etc.
- Optativas: calculadora.
Aquecimento
Proponha uma discussão que lembre a linguagem e os símbolos usados na representação dos intervalos.
Atividade principal
Proponha uma interação pela rede social escolhida: um jogo adaptado do plano original (que chamamos aqui de ping-pong-tchan) através da escolha de 3 grupos. Qualquer “jogador” pode pertencer a mais de um grupo.
Regras para cada rodada:
- O professor faz as perguntas;
- O grupo I dá a resposta (ping);
- O grupo II corrige, confirmando ou não e dando suas explicações (pong);
- O grupo III dá exemplos (tchan);
- Depois de cada rodada, os grupos mudam. Ou seja, o grupo I passa a ser o II, o II passa a ser o III e o III passa a ser o I, fazendo a rotação quando todos os grupos passarem por todas as etapas.
As perguntas podem ser (dependendo do tempo, pode-se propor mais uma rotação com mais três perguntas):
1) É possível escrever 3 na forma de fração e estimar a localização na reta numérica?
2) Quantos números existem num intervalo fechado de 1 até 8? Será que é possível estimar a localização de cada um deles?
3) O significa um intervalo ilimitado?
4) É possível que um intervalo tenha apenas números naturais?
5) O que significa dizer que um intervalo é aberto ou fechado?
6) Um intervalo semiaberto ou semifechado têm o mesmo significado?
Painel de soluções: respostas esperadas

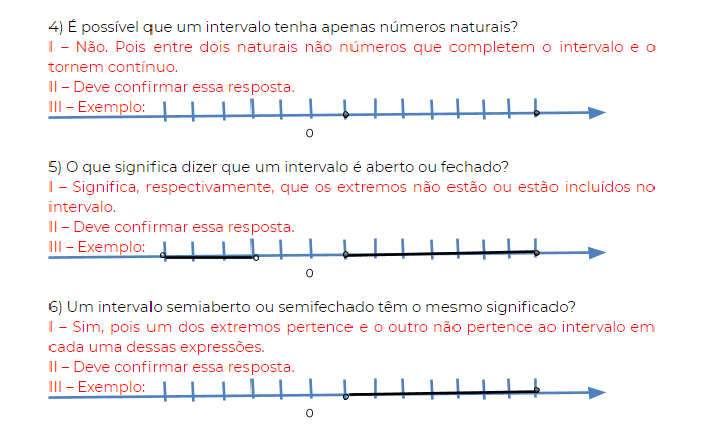
Sistematização e encerramento
A cada término de rotação, reforce as respostas corretas.
Este plano de aula foi elaborado pelo Time de autores NOVA ESCOLA
Autora: Maria Bernadete Estradioto
Mentor: Fernando de Mello Trevisani
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNC
EF09MA01; EF09MA02 - Ampliação dos campos numéricos: números reais (a necessidade de medir qualquer segmento de reta: números irracionais e seu significado; representação na reta numerada).
Objetivos específicos
Localização de números reais na reta real e em intervalos.
Conceito-chave
Localizar números reais na reta real e em intervalos.
Recursos necessários
Projetor ou impresso das atividades.
Pré-conhecimento da turma
- Intervalos abertos, fechados e semi abertos.
- Intervalos ilimitados.
- Números racionais e irracionais.