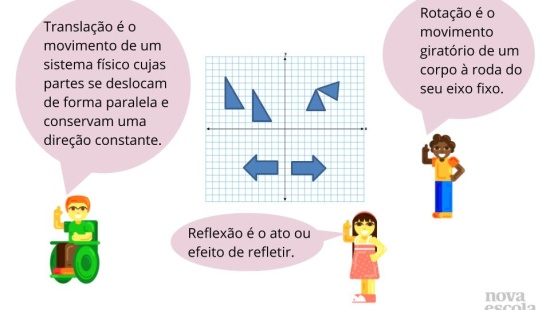
Retomada
Plano de Aula
Plano de aula: Transformações Equivalentes
Plano 4 de uma sequência de 10 planos. Veja todos os planos sobre Transformações isométricas e congruência de triângulos
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Renata Akemi Maekawa
Mentor: Fabricio Eduardo Ferreira
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
(EF08MA15) Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.
Objetivos Específicos
- Analisar como conjuntos de transformações isométricas modificam figuras no plano cartesiano.
- Compreender as características das transformações isométricas e de composições de transformações.
- Verificar equivalência entre conjuntos de transformações com e sem apoio de construções.
Conceito-chave
Composição de transformações isométricas no plano cartesiano
Recursos Necessários
- Lápis, tesoura e fichas impressas.
- Projetor (se possível)
Habilidades BNCC:
Objetivos de aprendizagem
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Renata Akemi Maekawa
Mentor: Fabricio Eduardo Ferreira
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
(EF08MA15) Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.
Objetivos Específicos
- Analisar como conjuntos de transformações isométricas modificam figuras no plano cartesiano.
- Compreender as características das transformações isométricas e de composições de transformações.
- Verificar equivalência entre conjuntos de transformações com e sem apoio de construções.
Conceito-chave
Composição de transformações isométricas no plano cartesiano
Recursos Necessários
- Lápis, tesoura e fichas impressas.
- Projetor (se possível)
Resumo da Aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Observação: É importante que os alunos tenham conhecimento das simetrias no plano cartesiano. Se considerar necessário, acesse os planos de aula sobre este tema na plataforma (unidades 15 e 16 do sétimo ano).
Retomada
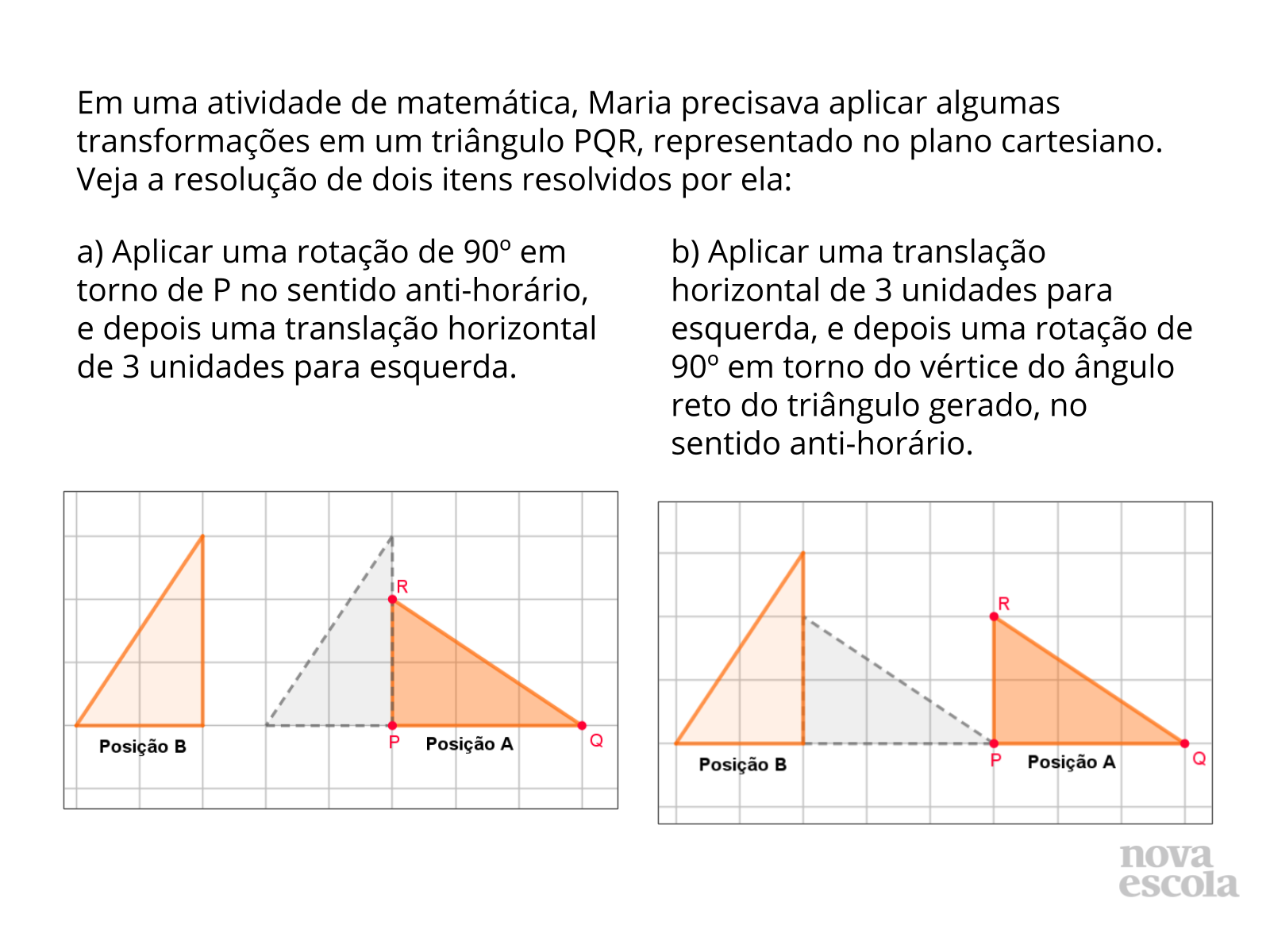
Tempo sugerido: 5 minutos (slides 3 e 4).
Orientações: Inicie a aula projetando a atividade ou desenhando as figuras, ou ainda, entregue cópias da atividade para os alunos. Leia o enunciado para os alunos e solicite que eles pensem individualmente na resposta e a anotem em seus cadernos. Oriente que eles analisem as figuras construídas e relacionem às transformações que aparecem no enunciado antes de elaborar a resposta para a pergunta proposta nesta atividade. Abra para que alguns alunos compartilhem suas respostas. Nesse momento, é importante enfatizar as estratégias que podem ser usadas para comparar transformações sem realizar as construções.
Propósito: Incentivar o aluno a analisar figuras geométricas congruentes no plano para verificar equivalência entre conjuntos de transformações.
Discuta com a Turma:
- Quais são as semelhanças e as diferenças entre as transformações propostas nos itens a e b do problema resolvido por Maria?
- Que estratégias podem ser usadas para comparar transformações sem realizar as construções?
Materiais complementares para impressão:
Retomada
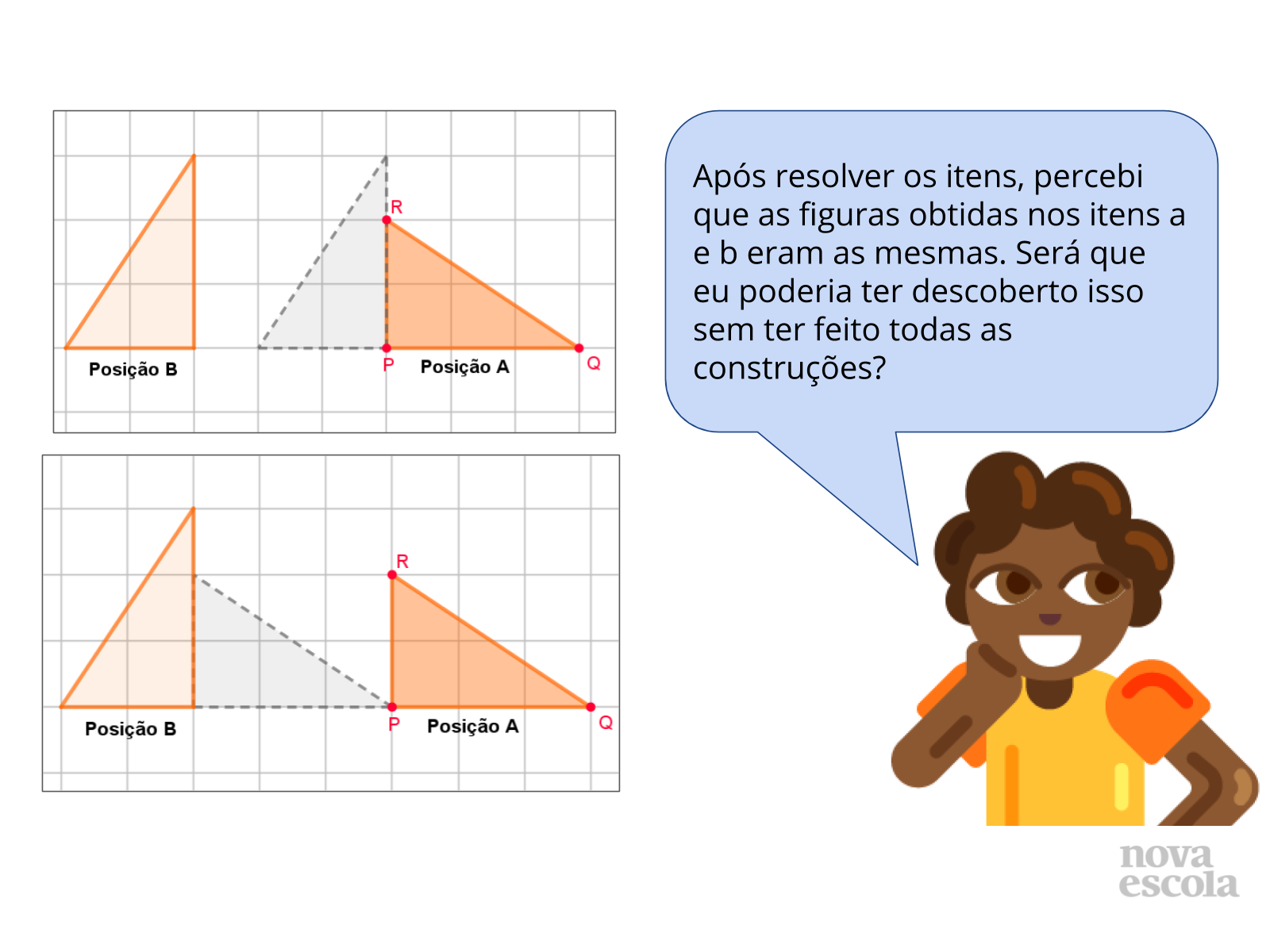
Tempo sugerido: 5 minutos (slides 3 e 4).
Orientações: Inicie a aula projetando a atividade ou desenhando as figuras, ou ainda, entregue cópias da atividade para os alunos. Leia o enunciado para os alunos e solicite que eles pensem individualmente na resposta e a anotem em seus cadernos. Oriente que eles analisem as figuras construídas e relacionem às transformações que aparecem no enunciado antes de elaborar a resposta para a pergunta proposta nesta atividade. Abra para que alguns alunos compartilhem suas respostas. Nesse momento, é importante enfatizar as estratégias que podem ser usadas para comparar transformações sem realizar as construções.
Propósito: Incentivar o aluno a analisar figuras geométricas congruentes no plano para verificar equivalência entre conjuntos de transformações.
Discuta com a Turma:
- Quais são as semelhanças e as diferenças entre as transformações propostas nos itens a e b do problema resolvido por Maria?
- Que estratégias podem ser usadas para comparar transformações sem realizar as construções?
Materiais complementares para impressão:
Atividade Principal

Tempo sugerido: 5 minutos.
Orientações: Projete esta atividade ou entregue cópia da atividade impressa, e leia o enunciado da questão para a classe (você também pode escolher alguns alunos para lerem em voz alta). Organize os alunos em duplas de trabalho heterogêneas. Solicite que os alunos pensem, individualmente, no problema e anotem as suas respostas em seus cadernos para, em seguida, lerem suas resoluções para a dupla, discutindo-as. Depois, abra para que os alunos compartilhem as suas respostas coletivamente. Nesse momento, é importante que os alunos expliquem como fizeram a verificação sem a construção das figuras, explicitando as características da transformação envolvida (translação).
Propósito: Incentivar que os alunos analisem transformações e suas características para determinar, sem realizar a construção, se existe equivalência entre conjuntos de transformações.
Discuta com a Turma:
- É possível afirmar que as dois alunos obterão o mesmo resultado sem fazer as construções?
- Como vocês convenceriam um colega, sem construir, que os resultados serão os mesmos ?
- Que características das translações foram importantes para você resolver esse problema? As direções das translações (para cima ou para baixo), foram importantes para resolver esse problema?
Materiais complementares para impressão:
Atividade Principal
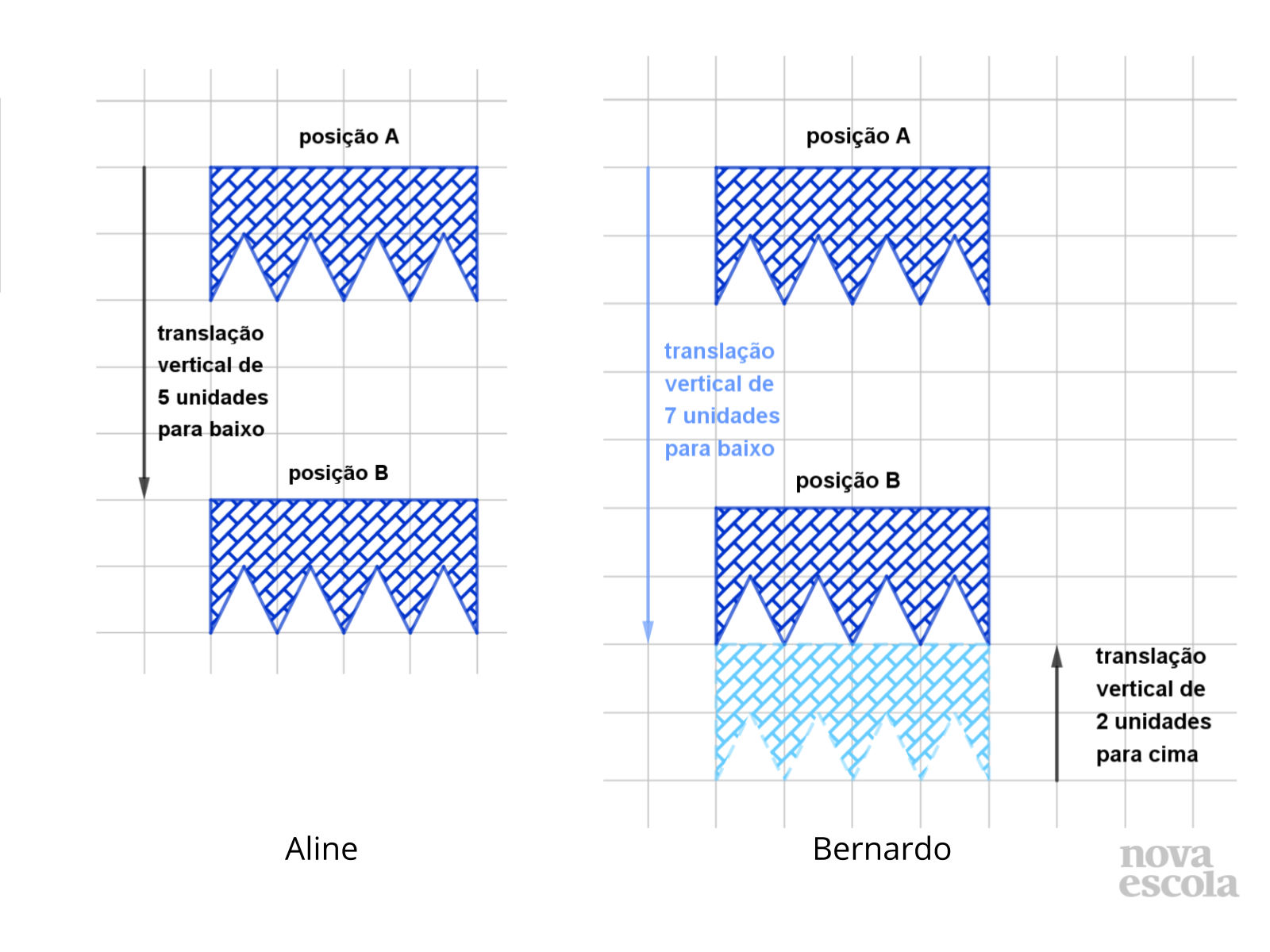
Tempo sugerido: 1 minuto.
Orientações: Após as discussões, apresentar as imagens que mostram as transformações propostas, confirmando a equivalência entre os dois conjuntos de transformações.
Propósito: Ilustrar aplicações de conjuntos de transformações, confirmando resultado obtido em discussão coletiva.
Materiais complementares para impressão:
Atividade Principal
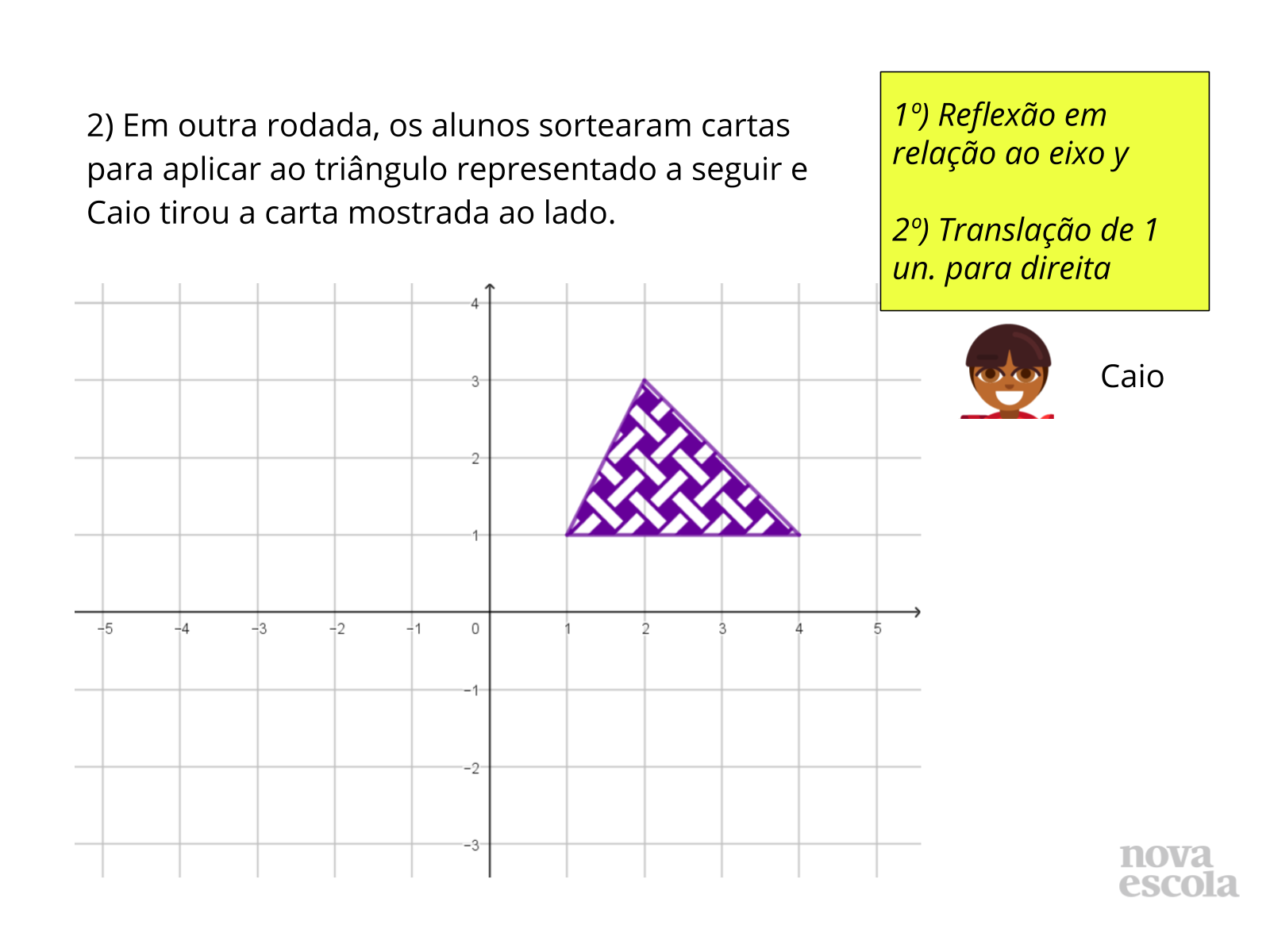
Tempo sugerido: 7 minutos (slides 7 e 8).
Orientações: Projete esta atividade (slides 7 e 8), leia o enunciado e dê continuidade à atividade impressa. Organize os alunos em quartetos (cada quarteto deve ser composto por duas duplas que estavam trabalhando juntas na atividade 1). Solicite que eles resolvam a atividade 2 nas duplas, anotando a resposta certa e os argumentos que utilizarão para explicar a escolha que fizeram. Ao terminarem, as duplas dos quartetos devem compartilhar as respostas obtidas umas com as outras, verificando se concordam com a resposta. Caso discordem, devem discutir até que todos os alunos do quarteto entrem em acordo. Nesse momento, circule pela sala para observar as discussões dos alunos, sem informar os grupos se a resposta obtida por eles está correta ou não.
Propósito: Incentivar que os alunos observem as características das transformações para determinar existência de equivalência entre elas.
Materiais complementares para impressão:
Atividade Principal

Tempo sugerido: 7 minutos (slides 7 e 8).
Orientações: Projete esta atividade (slides 7 e 8), leia o enunciado e dê continuidade à atividade impressa. Organize os alunos em quartetos (cada quarteto deve ser composto por duas duplas que estavam trabalhando juntas na atividade 1). Solicite que eles resolvam a atividade 2 nas duplas, anotando a resposta certa e os argumentos que utilizarão para explicar a escolha que fizeram. Ao terminarem, as duplas dos quartetos devem compartilhar as respostas obtidas umas com as outras, verificando se concordam com a resposta. Caso discordem, devem discutir até que todos os alunos do quarteto entrem em acordo. Nesse momento, circule pela sala para observar as discussões dos alunos, sem informar os grupos se a resposta obtida por eles está correta ou não.
Propósito: Incentivar que os alunos observem as características das transformações para determinar existência de equivalência entre elas.
Materiais complementares para impressão:
Resolução da Atividade Principal
Atividade Principal
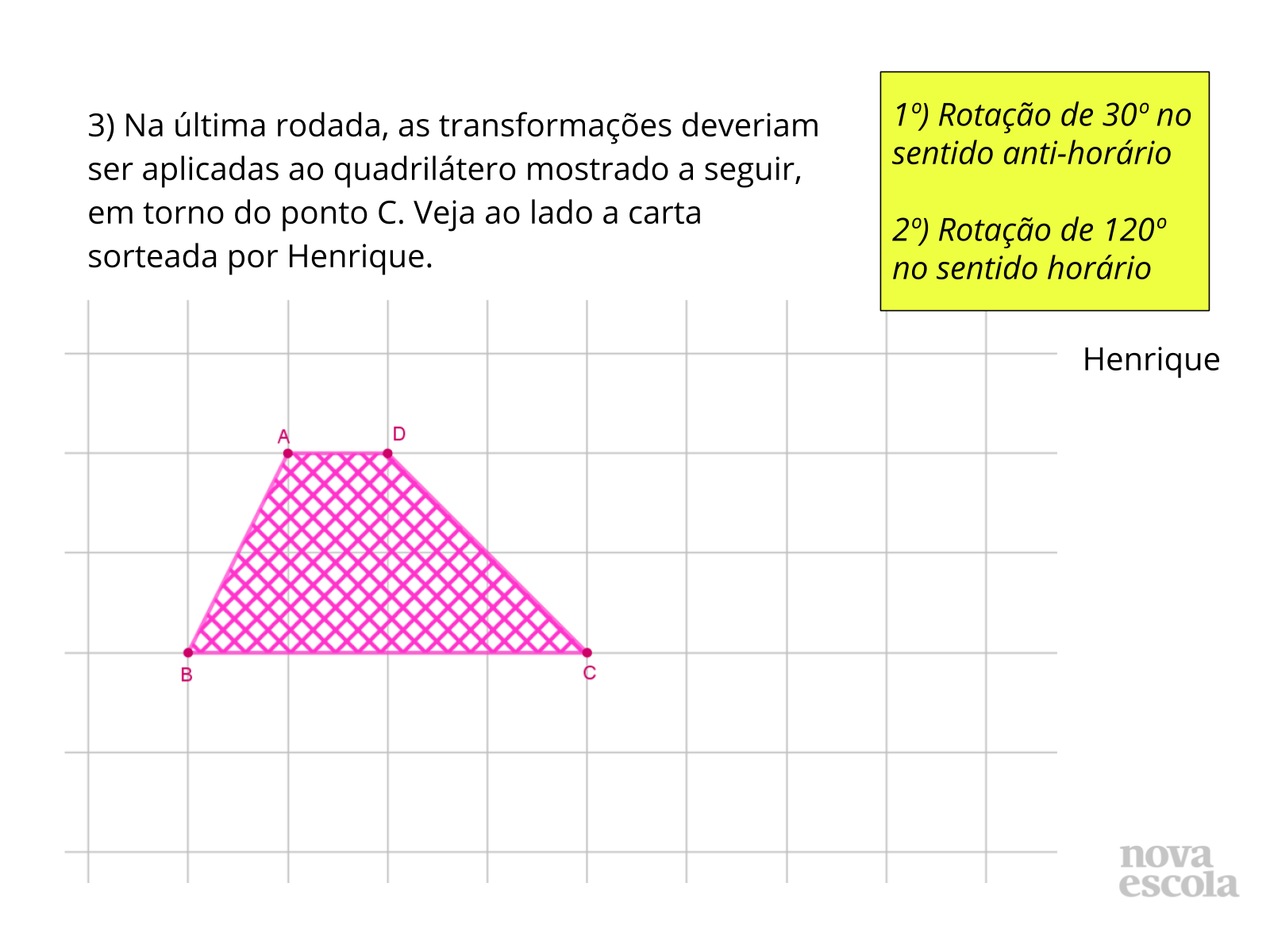 Atividade Principal
Atividade Principal Tempo sugerido: 8 minutos (slides 9 e 10).
Orientações: Projete esta atividade (slides 9 e 10), leia o enunciado e dê continuidade à atividade impressa. Solicite que eles resolvam a atividade 3 individualmente, anotando as transformações que pensaram para cada carta. Ao terminar, cada aluno deve ler as suas respostas, e todos do quarteto devem analisar e verificar se concordam com a resposta. Caso discordem, devem discutir até que todos os alunos do quarteto entrem em acordo. Para apoiar a discussão, podem recortar um quadrilátero ABCD para realizar manipulações com a figura (clique aqui para acessar o arquivo com a figura para recortar). Depois, devem fazer uma lista com todas as respostas que apareceram no quarteto, para se prepararem para a discussão coletiva que ocorrerá em seguida. Para os grupos que terminarem, proponha que elaborem novo conjunto de instruções, mas agora com rotações em torno de um ponto diferente do ponto C.
Enquanto os alunos resolvem a atividade 3, circule pela sala para observar as discussões dos alunos, sem informar os grupos se a resposta obtida por eles está correta ou não.
Propósito: Incentivar que os alunos observem as características das transformações para determinar existência de equivalência entre elas, analisando como uma composição de rotações (em torno do mesmo ponto), pode ser resumida em uma única rotação, e como os sentidos de rotação em uma composição influenciam o resultado final.
Materiais complementares para impressão:
Atividade Principal
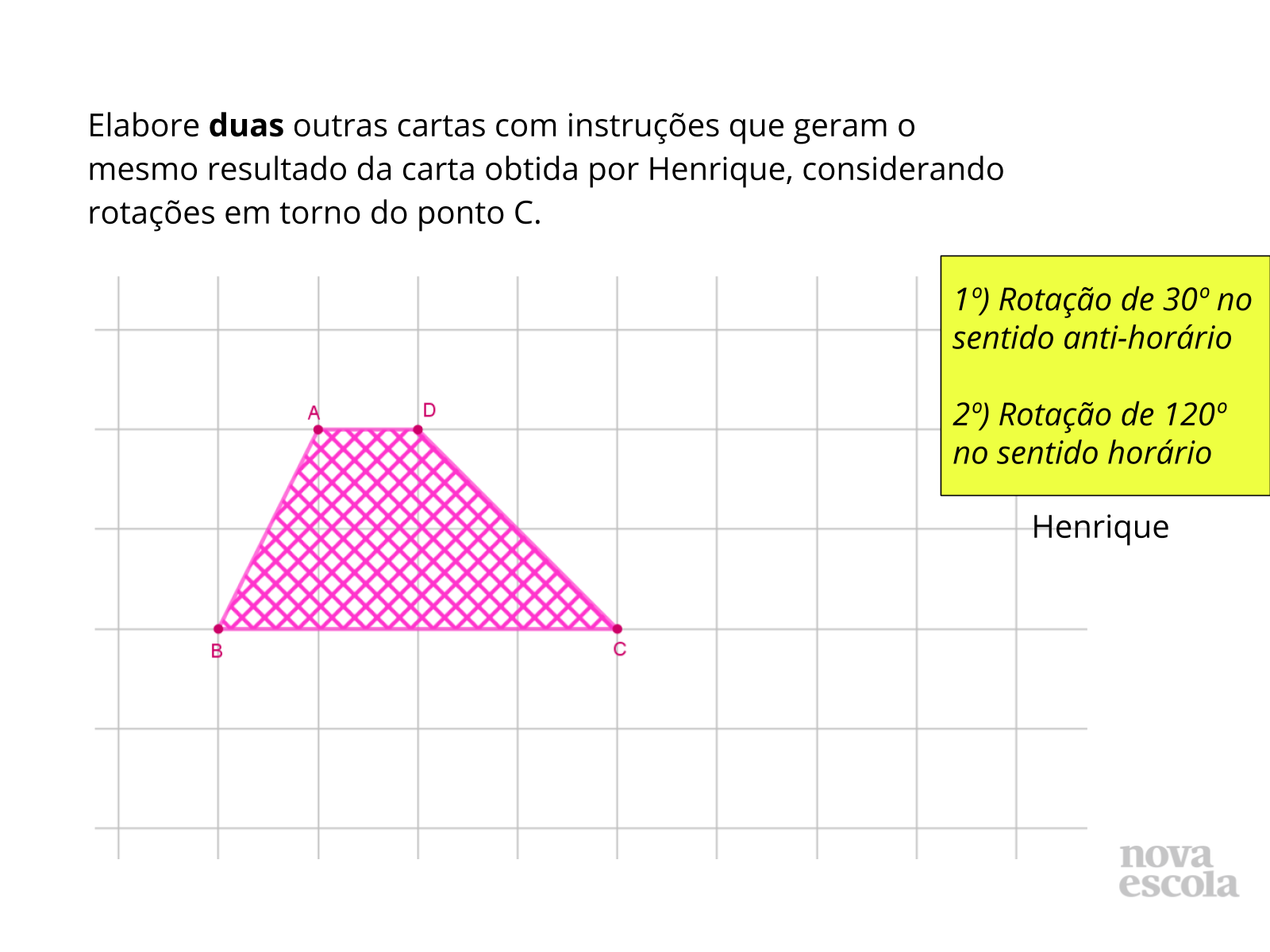 Atividade Principal
Atividade Principal Tempo sugerido: 8 minutos (slides 9 e 10).
Orientações: Projete esta atividade (slides 9 e 10), leia o enunciado e dê continuidade à atividade impressa. Solicite que eles resolvam a atividade 3 individualmente, anotando as transformações que pensaram para cada carta. Ao terminar, cada aluno deve ler as suas respostas, e todos do quarteto devem analisar e verificar se concordam com a resposta. Caso discordem, devem discutir até que todos os alunos do quarteto entrem em acordo. Para apoiar a discussão, podem recortar um quadrilátero ABCD para realizar manipulações com a figura (clique aqui para acessar o arquivo com a figura para recortar). Depois, devem fazer uma lista com todas as respostas que apareceram no quarteto, para se prepararem para a discussão coletiva que ocorrerá em seguida. Para os grupos que terminarem, proponha que elaborem novo conjunto de instruções, mas agora com rotações em torno de um ponto diferente do ponto C.
Enquanto os alunos resolvem a atividade 3, circule pela sala para observar as discussões dos alunos, sem informar os grupos se a resposta obtida por eles está correta ou não.
Propósito: Incentivar que os alunos observem as características das transformações para determinar existência de equivalência entre elas, analisando como uma composição de rotações (em torno do mesmo ponto), pode ser resumida em uma única rotação, e como os sentidos de rotação em uma composição influenciam o resultado final.
Materiais complementares para impressão:
Discussão das Soluções
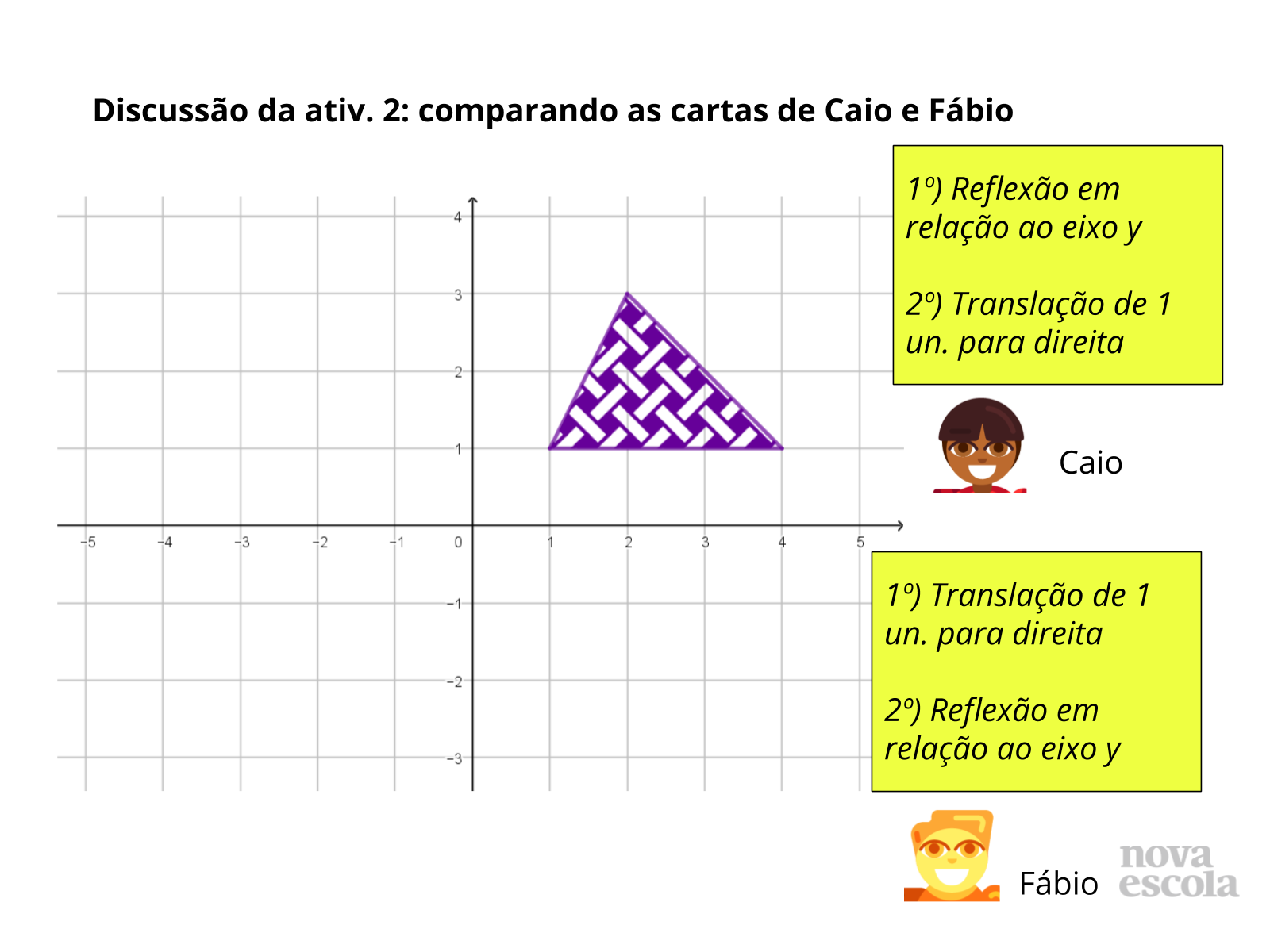
Tempo sugerido: 7 minutos. (Slides de 11 a 17).
Orientações: Retome as instruções das cartas que serão comparadas (Caio e Fábio no slide 11, Caio e Emília no slide 14 e Caio e Gabriela no slide 16), sem mostrar as construções das figuras obtidas por eles. Estes slides facilitam mostrar apenas as cartas antes das construções. As etapas das construções aparecerão a cada slide. Abra para que os alunos compartilhem as estratégias que utilizaram para realizar a comparação, descrevendo as características das transformações listadas em cada carta. Em seguida, abra para que a turma discuta e decida se concordam com a solução apresentada. Depois exiba as construções, retomando com o apoio da imagem as estratégias de comparação que foram discutidas.
Propósito: Analisar como as transformações modificam as imagens e compreender estratégias para determinar se existe equivalência entre conjuntos de transformações.
Discuta com a Turma:
- Como as translações alteram a posição da figura?
- Como as reflexões alteram a posição da figura? Para que “parte” do plano cartesiano a figura é levada após uma reflexão?
- O que acontece com a distância em relação ao eixo y em cada caso?
- Quais estratégias podemos utilizar para verificar se as cartas são equivalentes?
Discussão das Soluções
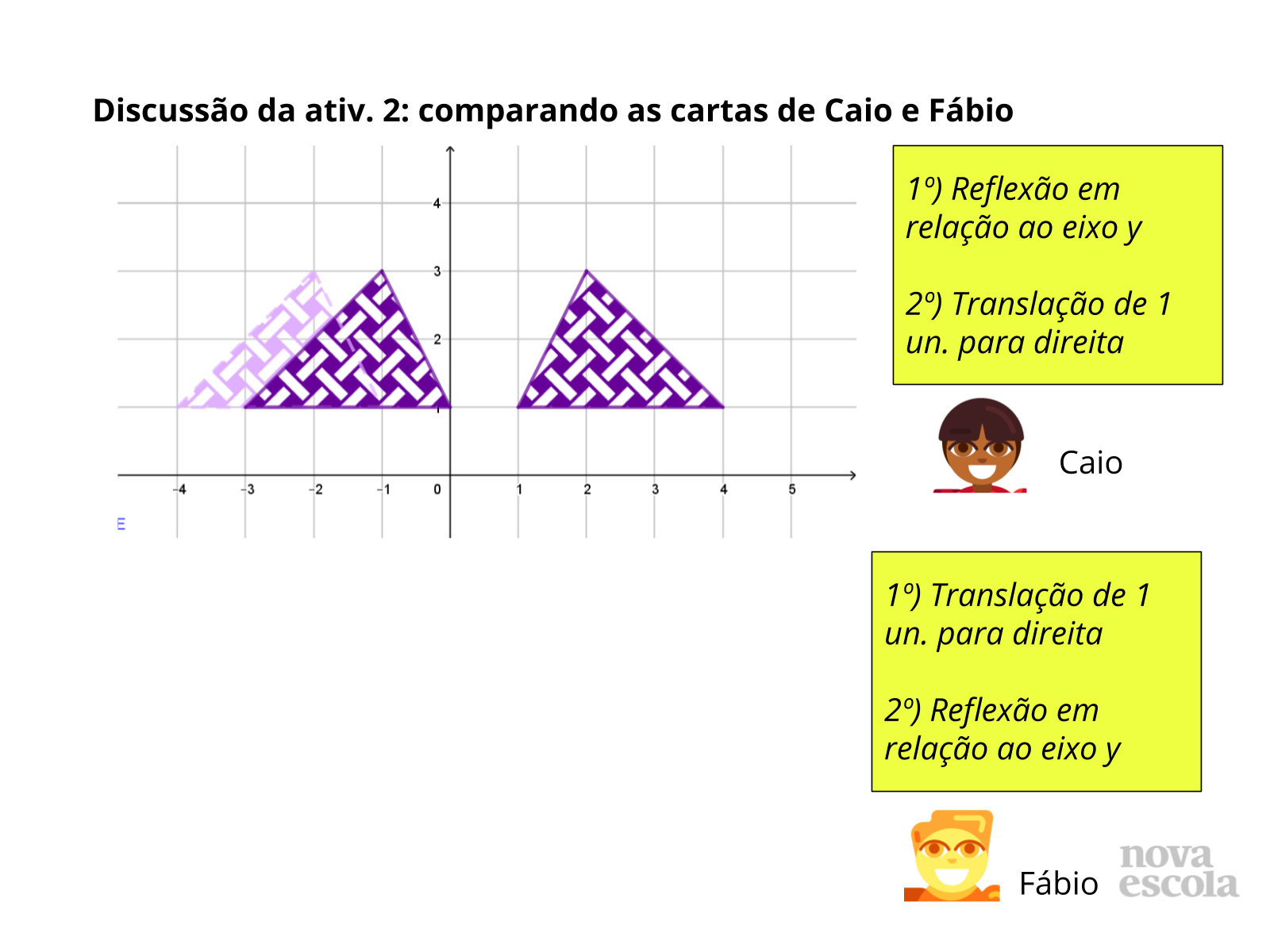
Tempo sugerido: 7 minutos. (Slides de 11 a 17).
Orientações: Retome as instruções das cartas que serão comparadas (Caio e Fábio no slide 11, Caio e Emília no slide 14 e Caio e Gabriela no slide 16), sem mostrar as construções das figuras obtidas por eles. Estes slides facilitam mostrar apenas as cartas antes das construções. As etapas das construções aparecerão a cada slide. Abra para que os alunos compartilhem as estratégias que utilizaram para realizar a comparação, descrevendo as características das transformações listadas em cada carta. Em seguida, abra para que a turma discuta e decida se concordam com a solução apresentada. Depois exiba as construções, retomando com o apoio da imagem as estratégias de comparação que foram discutidas.
Propósito: Analisar como as transformações modificam as imagens e compreender estratégias para determinar se existe equivalência entre conjuntos de transformações.
Discuta com a Turma:
- Como as translações alteram a posição da figura?
- Como as reflexões alteram a posição da figura? Para que “parte” do plano cartesiano a figura é levada após uma reflexão?
- O que acontece com a distância em relação ao eixo y em cada caso?
- Quais estratégias podemos utilizar para verificar se as cartas são equivalentes?
Discussão das Soluções
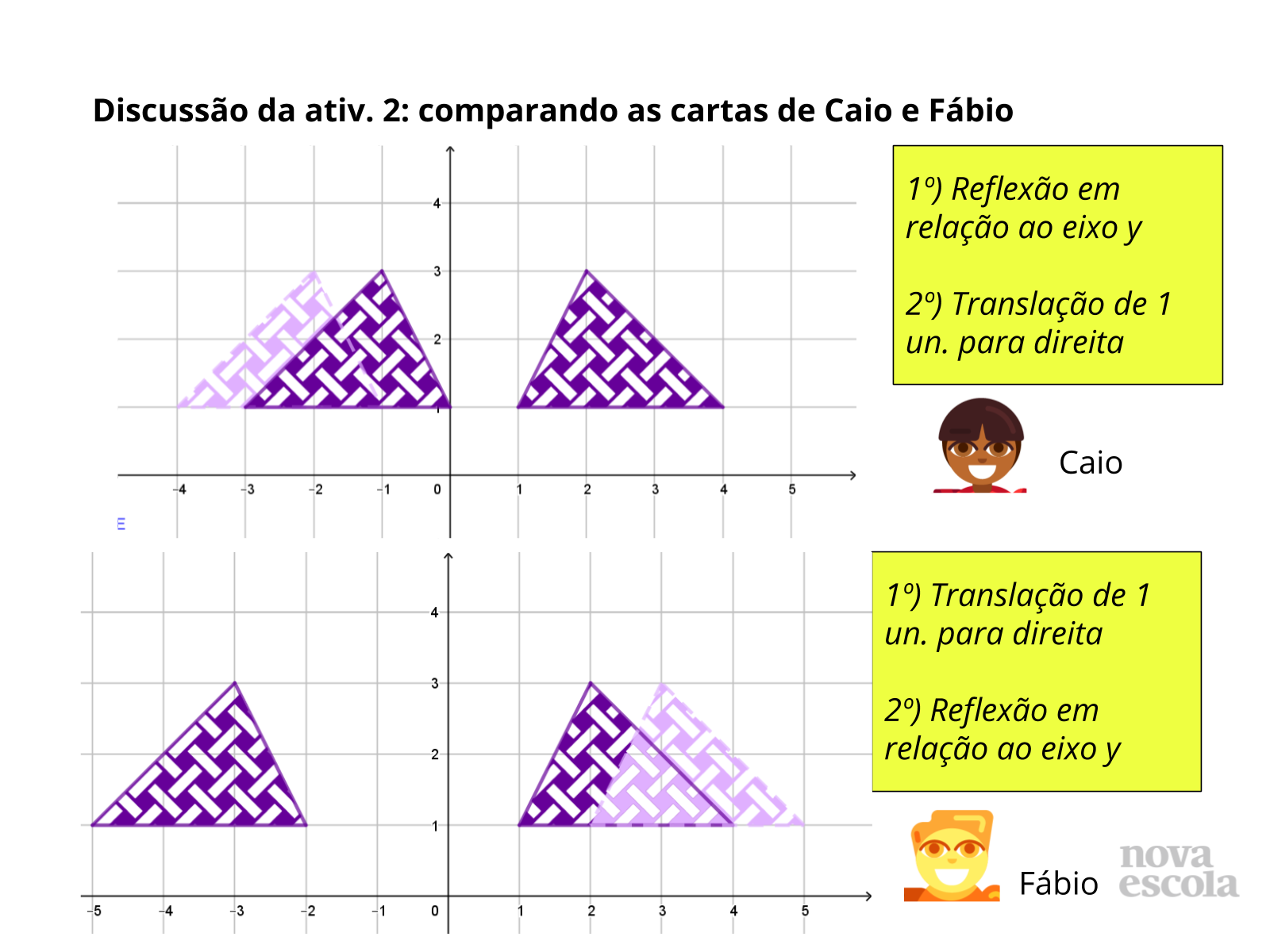
Tempo sugerido: 7 minutos. (Slides de 11 a 17).
Orientações: Retome as instruções das cartas que serão comparadas (Caio e Fábio no slide 11, Caio e Emília no slide 14 e Caio e Gabriela no slide 16), sem mostrar as construções das figuras obtidas por eles. Estes slides facilitam mostrar apenas as cartas antes das construções. As etapas das construções aparecerão a cada slide. Abra para que os alunos compartilhem as estratégias que utilizaram para realizar a comparação, descrevendo as características das transformações listadas em cada carta. Em seguida, abra para que a turma discuta e decida se concordam com a solução apresentada. Depois exiba as construções, retomando com o apoio da imagem as estratégias de comparação que foram discutidas.
Propósito: Analisar como as transformações modificam as imagens e compreender estratégias para determinar se existe equivalência entre conjuntos de transformações.
Discuta com a Turma:
- Como as translações alteram a posição da figura?
- Como as reflexões alteram a posição da figura? Para que “parte” do plano cartesiano a figura é levada após uma reflexão?
- O que acontece com a distância em relação ao eixo y em cada caso?
- Quais estratégias podemos utilizar para verificar se as cartas são equivalentes?
Discussão das Soluções
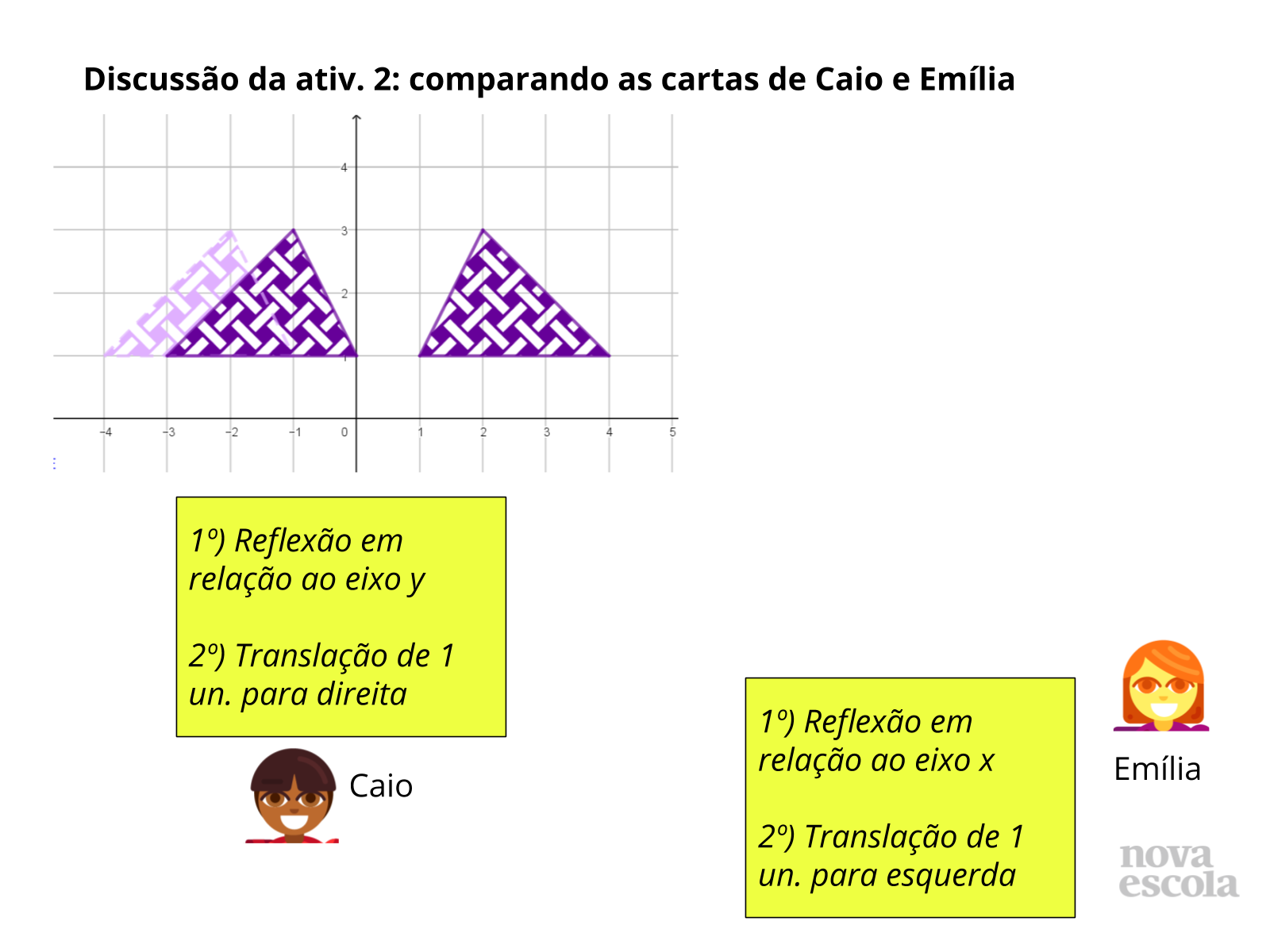
Tempo sugerido: 7 minutos. (Slides de 11 a 17).
Orientações: Retome as instruções das cartas que serão comparadas (Caio e Fábio no slide 11, Caio e Emília no slide 14 e Caio e Gabriela no slide 16), sem mostrar as construções das figuras obtidas por eles. Estes slides facilitam mostrar apenas as cartas antes das construções. As etapas das construções aparecerão a cada slide. Abra para que os alunos compartilhem as estratégias que utilizaram para realizar a comparação, descrevendo as características das transformações listadas em cada carta. Em seguida, abra para que a turma discuta e decida se concordam com a solução apresentada. Depois exiba as construções, retomando com o apoio da imagem as estratégias de comparação que foram discutidas.
Propósito: Analisar como as transformações modificam as imagens e compreender estratégias para determinar se existe equivalência entre conjuntos de transformações.
Discuta com a Turma:
- Como as translações alteram a posição da figura?
- Como as reflexões alteram a posição da figura? Para que “parte” do plano cartesiano a figura é levada após uma reflexão?
- O que acontece com a distância em relação ao eixo y em cada caso?
- Quais estratégias podemos utilizar para verificar se as cartas são equivalentes?
Discussão das Soluções
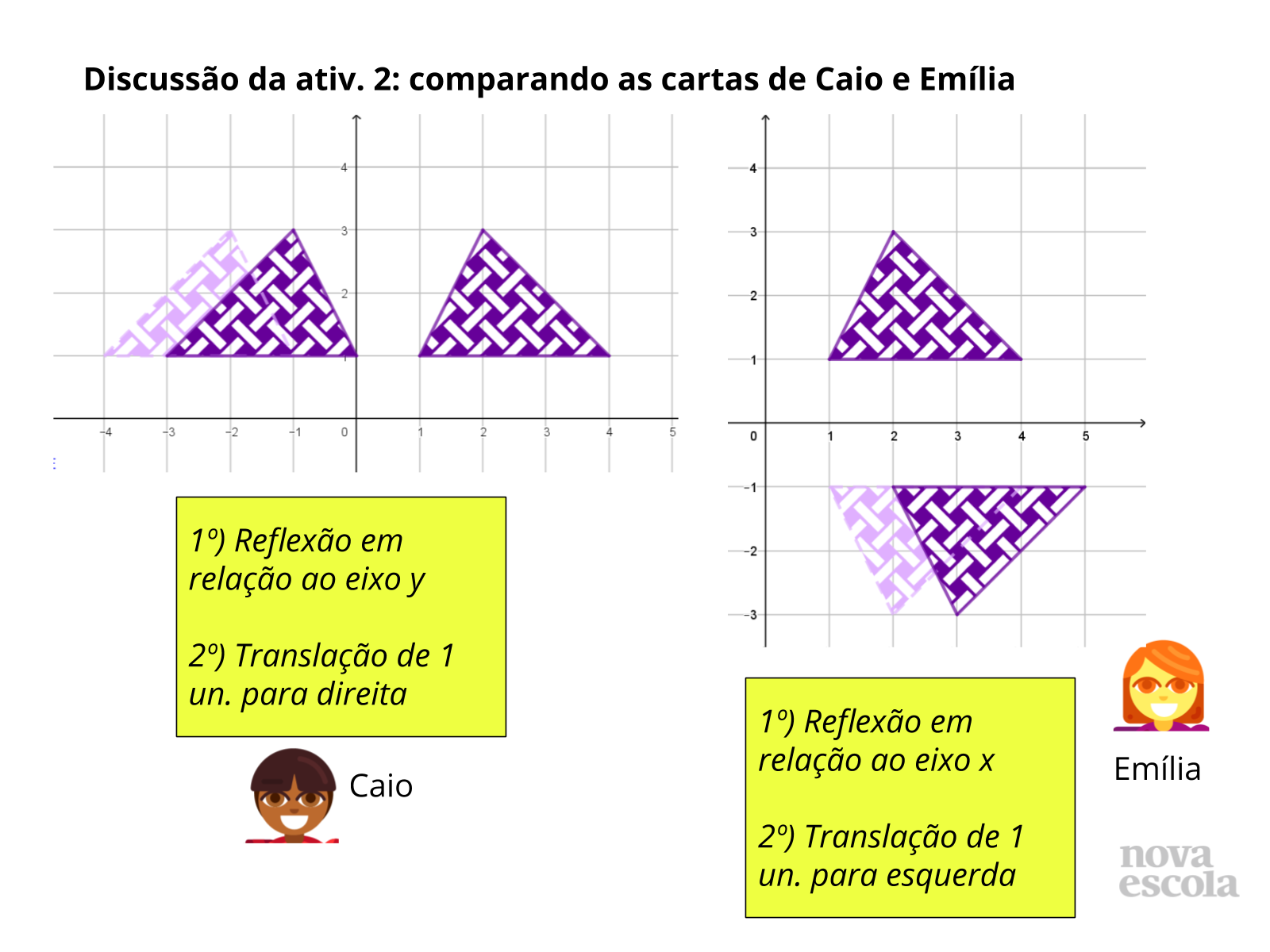
Tempo sugerido: 7 minutos. (Slides de 11 a 17).
Orientações: Retome as instruções das cartas que serão comparadas (Caio e Fábio no slide 11, Caio e Emília no slide 14 e Caio e Gabriela no slide 16), sem mostrar as construções das figuras obtidas por eles. Estes slides facilitam mostrar apenas as cartas antes das construções. As etapas das construções aparecerão a cada slide. Abra para que os alunos compartilhem as estratégias que utilizaram para realizar a comparação, descrevendo as características das transformações listadas em cada carta. Em seguida, abra para que a turma discuta e decida se concordam com a solução apresentada. Depois exiba as construções, retomando com o apoio da imagem as estratégias de comparação que foram discutidas.
Propósito: Analisar como as transformações modificam as imagens e compreender estratégias para determinar se existe equivalência entre conjuntos de transformações.
Discuta com a Turma:
- Como as translações alteram a posição da figura?
- Como as reflexões alteram a posição da figura? Para que “parte” do plano cartesiano a figura é levada após uma reflexão?
- O que acontece com a distância em relação ao eixo y em cada caso?
- Quais estratégias podemos utilizar para verificar se as cartas são equivalentes?
Discussão das Soluções
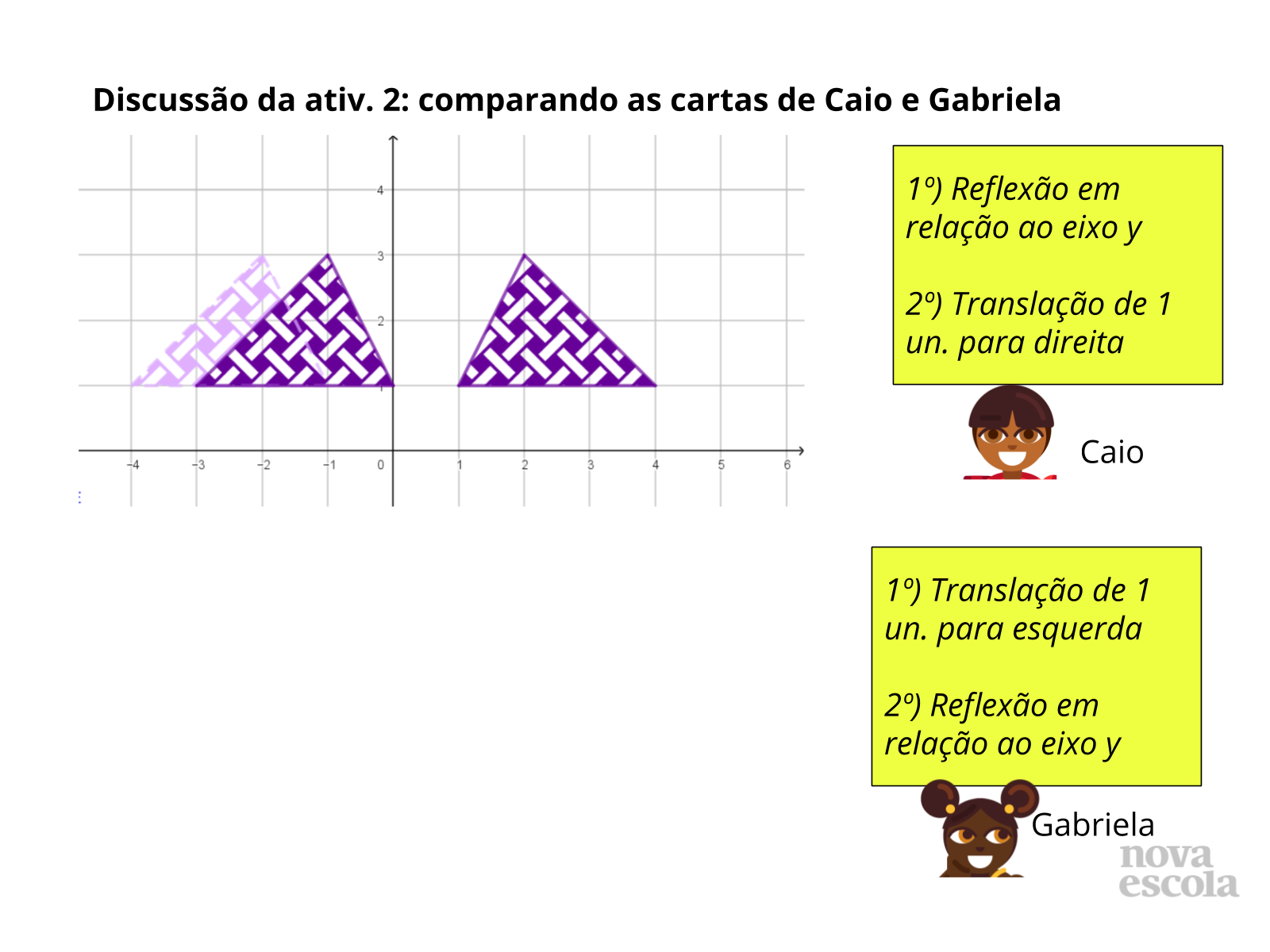
Tempo sugerido: 7 minutos. (Slides de 11 a 17).
Orientações: Retome as instruções das cartas que serão comparadas (Caio e Fábio no slide 11, Caio e Emília no slide 14 e Caio e Gabriela no slide 16), sem mostrar as construções das figuras obtidas por eles. Estes slides facilitam mostrar apenas as cartas antes das construções. As etapas das construções aparecerão a cada slide. Abra para que os alunos compartilhem as estratégias que utilizaram para realizar a comparação, descrevendo as características das transformações listadas em cada carta. Em seguida, abra para que a turma discuta e decida se concordam com a solução apresentada. Depois exiba as construções, retomando com o apoio da imagem as estratégias de comparação que foram discutidas.
Propósito: Analisar como as transformações modificam as imagens e compreender estratégias para determinar se existe equivalência entre conjuntos de transformações.
Discuta com a Turma:
- Como as translações alteram a posição da figura?
- Como as reflexões alteram a posição da figura? Para que “parte” do plano cartesiano a figura é levada após uma reflexão?
- O que acontece com a distância em relação ao eixo y em cada caso?
- Quais estratégias podemos utilizar para verificar se as cartas são equivalentes?
Discussão das Soluções
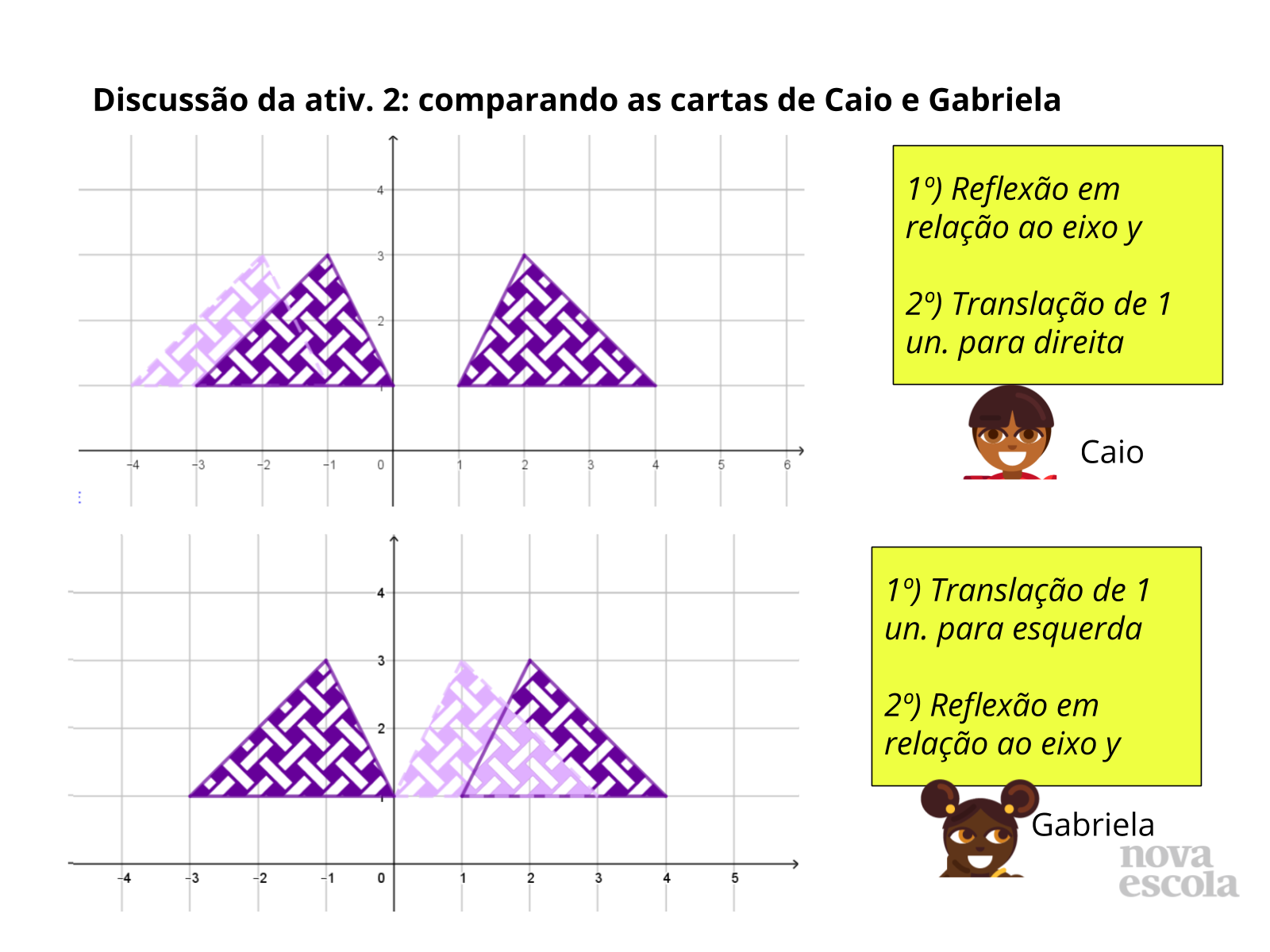
Tempo sugerido: 7 minutos. (Slides de 11 a 17).
Orientações: Retome as instruções das cartas que serão comparadas (Caio e Fábio no slide 11, Caio e Emília no slide 14 e Caio e Gabriela no slide 16), sem mostrar as construções das figuras obtidas por eles. Estes slides facilitam mostrar apenas as cartas antes das construções. As etapas das construções aparecerão a cada slide. Abra para que os alunos compartilhem as estratégias que utilizaram para realizar a comparação, descrevendo as características das transformações listadas em cada carta. Em seguida, abra para que a turma discuta e decida se concordam com a solução apresentada. Depois exiba as construções, retomando com o apoio da imagem as estratégias de comparação que foram discutidas.
Propósito: Analisar como as transformações modificam as imagens e compreender estratégias para determinar se existe equivalência entre conjuntos de transformações.
Discuta com a Turma:
- Como as translações alteram a posição da figura?
- Como as reflexões alteram a posição da figura? Para que “parte” do plano cartesiano a figura é levada após uma reflexão?
- O que acontece com a distância em relação ao eixo y em cada caso?
- Quais estratégias podemos utilizar para verificar se as cartas são equivalentes?
Discussão das Soluções
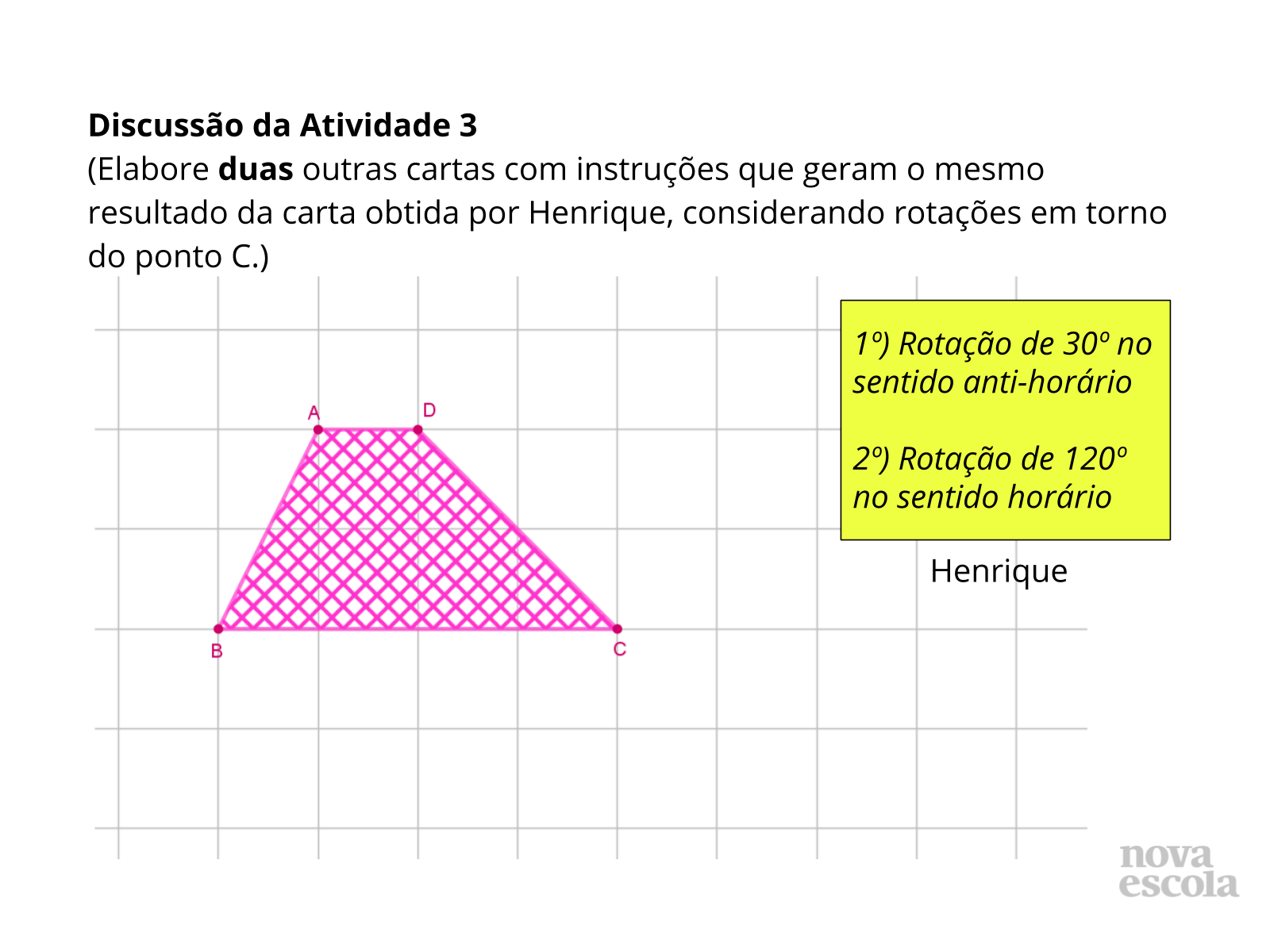
Tempo sugerido: 8 minutos. (Slides 18 a 22).
Orientações: A partir da observação feita na etapa anterior, busque chamar grupos que tiveram respostas diferentes para participar da discussão. Peça para que os grupos leiam as suas respostas e expliquem para a classe as estratégias que utilizaram para chegar a essa resposta. Após o compartilhamento de cada resposta, abra para que a turma discuta e decida de concorda com a solução apresentada.
Nesse momento é importante que os alunos compreendam como podem analisar as rotações da composição para antecipar como será a imagem final. Acesse o arquivo com a resolução da atividade para ler mais sobre as possibilidades de resolução desta atividade.
Utilize o slide 20 para exibir como as transformações da carta de Henrique alteram a figura e para apoiar a discussão sobre composições de rotações com sentidos diferentes.
Utilize o slide 22 para apoiar a discussão sobre composições de rotações com sentidos iguais.
As etapas das construções aparecerão a cada slide.
Propósito: Incentivar que os alunos observem as características das transformações para determinar existência de equivalência entre elas, analisando como uma composição de rotações (em torno do mesmo ponto), pode ser resumida em uma única rotação, e como os sentidos de rotações em uma composição influenciam o resultado final.
Discuta com a Turma:
- O que acontece quando os sentidos das rotações que aparecem na composição são diferentes?
- O que acontece quando os sentidos das rotações que aparecem na composição são iguais?
- Será que toda composição de rotações em torno de um mesmo ponto pode ser resumida em uma única rotação?
- Quantas respostas diferentes esse problema possui?
Discussão das Soluções

Tempo sugerido: 8 minutos. (Slides 18 a 22).
Orientações: A partir da observação feita na etapa anterior, busque chamar grupos que tiveram respostas diferentes para participar da discussão. Peça para que os grupos leiam as suas respostas e expliquem para a classe as estratégias que utilizaram para chegar a essa resposta. Após o compartilhamento de cada resposta, abra para que a turma discuta e decida de concorda com a solução apresentada.
Nesse momento é importante que os alunos compreendam como podem analisar as rotações da composição para antecipar como será a imagem final. Acesse o arquivo com a resolução da atividade para ler mais sobre as possibilidades de resolução desta atividade.
Utilize o slide 20 para exibir como as transformações da carta de Henrique alteram a figura e para apoiar a discussão sobre composições de rotações com sentidos diferentes.
Utilize o slide 22 para apoiar a discussão sobre composições de rotações com sentidos iguais.
As etapas das construções aparecerão a cada slide.
Propósito: Incentivar que os alunos observem as características das transformações para determinar existência de equivalência entre elas, analisando como uma composição de rotações (em torno do mesmo ponto), pode ser resumida em uma única rotação, e como os sentidos de rotações em uma composição influenciam o resultado final.
Discuta com a Turma:
- O que acontece quando os sentidos das rotações que aparecem na composição são diferentes?
- O que acontece quando os sentidos das rotações que aparecem na composição são iguais?
- Será que toda composição de rotações em torno de um mesmo ponto pode ser resumida em uma única rotação?
- Quantas respostas diferentes esse problema possui?
Discussão das Soluções
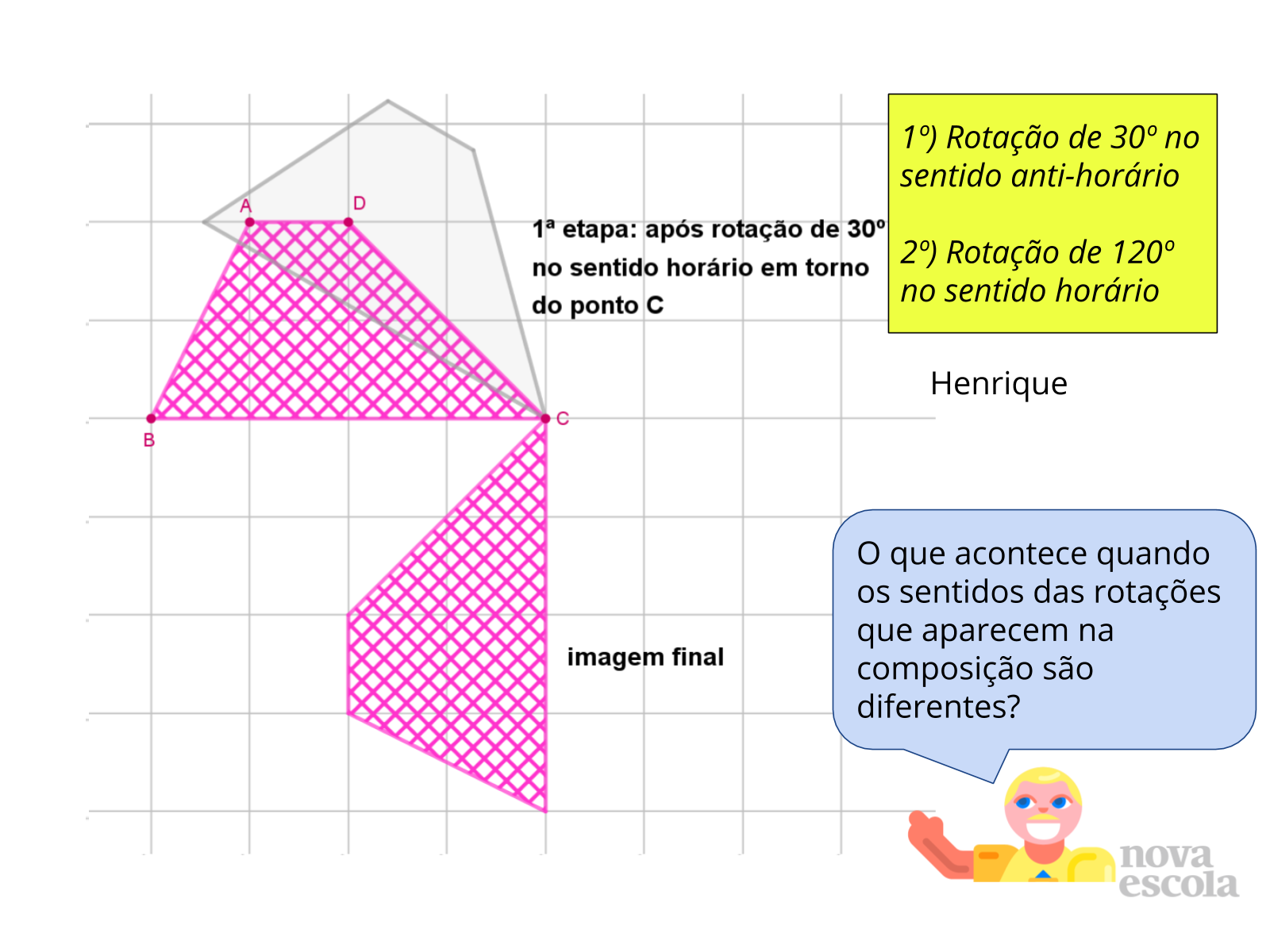
Tempo sugerido: 8 minutos. (Slides 18 a 22).
Orientações: A partir da observação feita na etapa anterior, busque chamar grupos que tiveram respostas diferentes para participar da discussão. Peça para que os grupos leiam as suas respostas e expliquem para a classe as estratégias que utilizaram para chegar a essa resposta. Após o compartilhamento de cada resposta, abra para que a turma discuta e decida de concorda com a solução apresentada.
Nesse momento é importante que os alunos compreendam como podem analisar as rotações da composição para antecipar como será a imagem final. Acesse o arquivo com a resolução da atividade para ler mais sobre as possibilidades de resolução desta atividade.
Utilize o slide 20 para exibir como as transformações da carta de Henrique alteram a figura e para apoiar a discussão sobre composições de rotações com sentidos diferentes.
Utilize o slide 22 para apoiar a discussão sobre composições de rotações com sentidos iguais.
As etapas das construções aparecerão a cada slide.
Propósito: Incentivar que os alunos observem as características das transformações para determinar existência de equivalência entre elas, analisando como uma composição de rotações (em torno do mesmo ponto), pode ser resumida em uma única rotação, e como os sentidos de rotações em uma composição influenciam o resultado final.
Discuta com a Turma:
- O que acontece quando os sentidos das rotações que aparecem na composição são diferentes?
- O que acontece quando os sentidos das rotações que aparecem na composição são iguais?
- Será que toda composição de rotações em torno de um mesmo ponto pode ser resumida em uma única rotação?
- Quantas respostas diferentes esse problema possui?
Discussão das Soluções

Tempo sugerido: 8 minutos. (Slides 18 a 22).
Orientações: A partir da observação feita na etapa anterior, busque chamar grupos que tiveram respostas diferentes para participar da discussão. Peça para que os grupos leiam as suas respostas e expliquem para a classe as estratégias que utilizaram para chegar a essa resposta. Após o compartilhamento de cada resposta, abra para que a turma discuta e decida de concorda com a solução apresentada.
Nesse momento é importante que os alunos compreendam como podem analisar as rotações da composição para antecipar como será a imagem final. Acesse o arquivo com a resolução da atividade para ler mais sobre as possibilidades de resolução desta atividade.
Utilize o slide 20 para exibir como as transformações da carta de Henrique alteram a figura e para apoiar a discussão sobre composições de rotações com sentidos diferentes.
Utilize o slide 22 para apoiar a discussão sobre composições de rotações com sentidos iguais.
As etapas das construções aparecerão a cada slide.
Propósito: Incentivar que os alunos observem as características das transformações para determinar existência de equivalência entre elas, analisando como uma composição de rotações (em torno do mesmo ponto), pode ser resumida em uma única rotação, e como os sentidos de rotações em uma composição influenciam o resultado final.
Discuta com a Turma:
- O que acontece quando os sentidos das rotações que aparecem na composição são diferentes?
- O que acontece quando os sentidos das rotações que aparecem na composição são iguais?
- Será que toda composição de rotações em torno de um mesmo ponto pode ser resumida em uma única rotação?
- Quantas respostas diferentes esse problema possui?
Discussão das Soluções
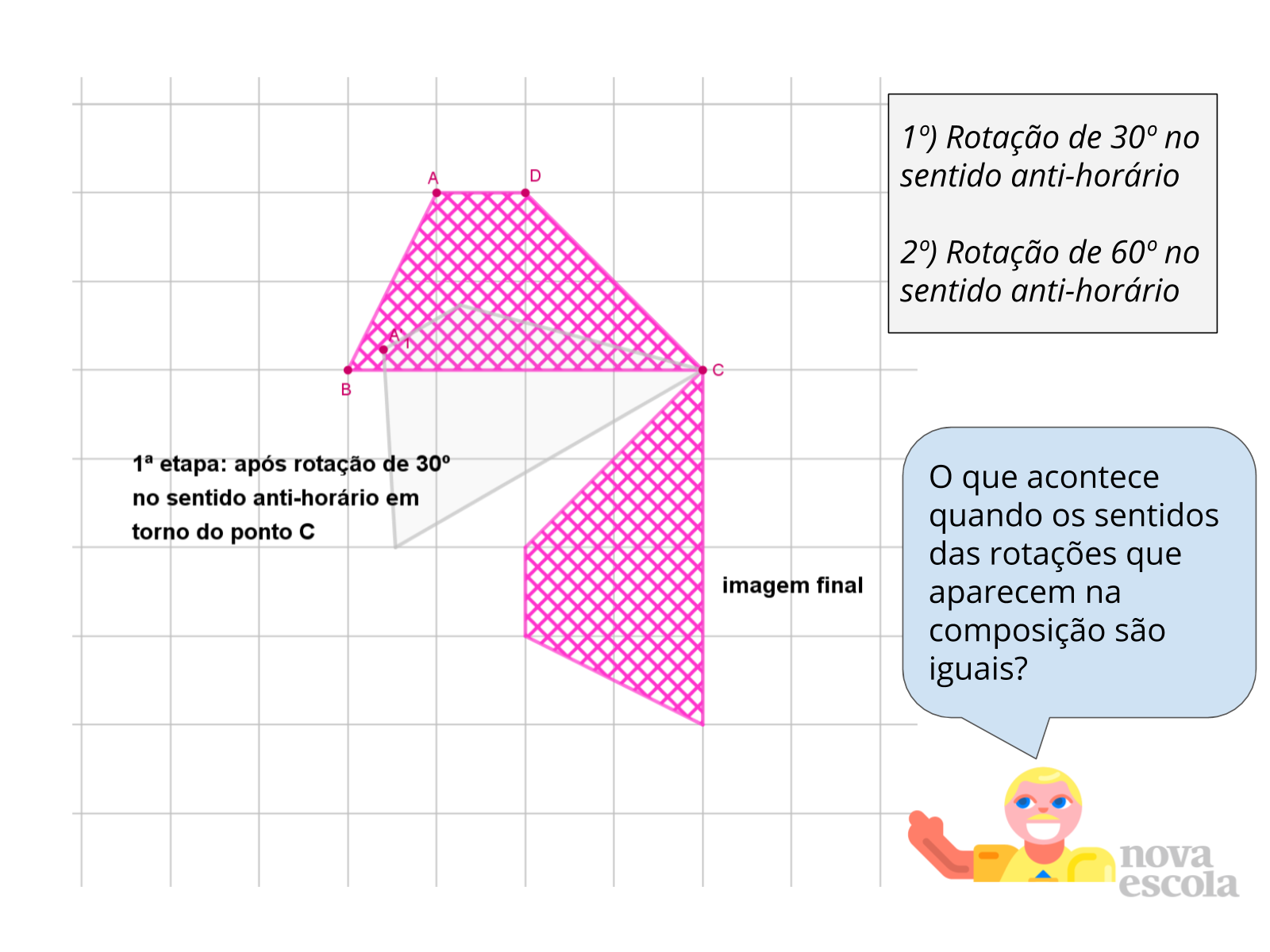
Tempo sugerido: 8 minutos. (Slides 18 a 22).
Orientações: A partir da observação feita na etapa anterior, busque chamar grupos que tiveram respostas diferentes para participar da discussão. Peça para que os grupos leiam as suas respostas e expliquem para a classe as estratégias que utilizaram para chegar a essa resposta. Após o compartilhamento de cada resposta, abra para que a turma discuta e decida de concorda com a solução apresentada.
Nesse momento é importante que os alunos compreendam como podem analisar as rotações da composição para antecipar como será a imagem final. Acesse o arquivo com a resolução da atividade para ler mais sobre as possibilidades de resolução desta atividade.
Utilize o slide 20 para exibir como as transformações da carta de Henrique alteram a figura e para apoiar a discussão sobre composições de rotações com sentidos diferentes.
Utilize o slide 22 para apoiar a discussão sobre composições de rotações com sentidos iguais.
As etapas das construções aparecerão a cada slide.
Propósito: Incentivar que os alunos observem as características das transformações para determinar existência de equivalência entre elas, analisando como uma composição de rotações (em torno do mesmo ponto), pode ser resumida em uma única rotação, e como os sentidos de rotações em uma composição influenciam o resultado final.
Discuta com a Turma:
- O que acontece quando os sentidos das rotações que aparecem na composição são diferentes?
- O que acontece quando os sentidos das rotações que aparecem na composição são iguais?
- Será que toda composição de rotações em torno de um mesmo ponto pode ser resumida em uma única rotação?
- Quantas respostas diferentes esse problema possui?
Encerramento

Tempo sugerido: 2 minutos.
Orientações: Solicite que os alunos digam quais foram os pontos mais importantes trabalhados em aula (antes de exibir o slide). Depois, leia o texto desse slide, ou peça para algum aluno ler, para sistematizar as aprendizagens da aula, verificando se algum ponto não havia sido destacado pelos alunos e/ou completando a sistematização da aula com pontos levantados pelos alunos que não estão escritos.
Propósito: Retomar as aprendizagens da aula, destacando aspectos importantes que devem ser analisados quando se trabalha com conjuntos de transformações isométricas.
Raio X
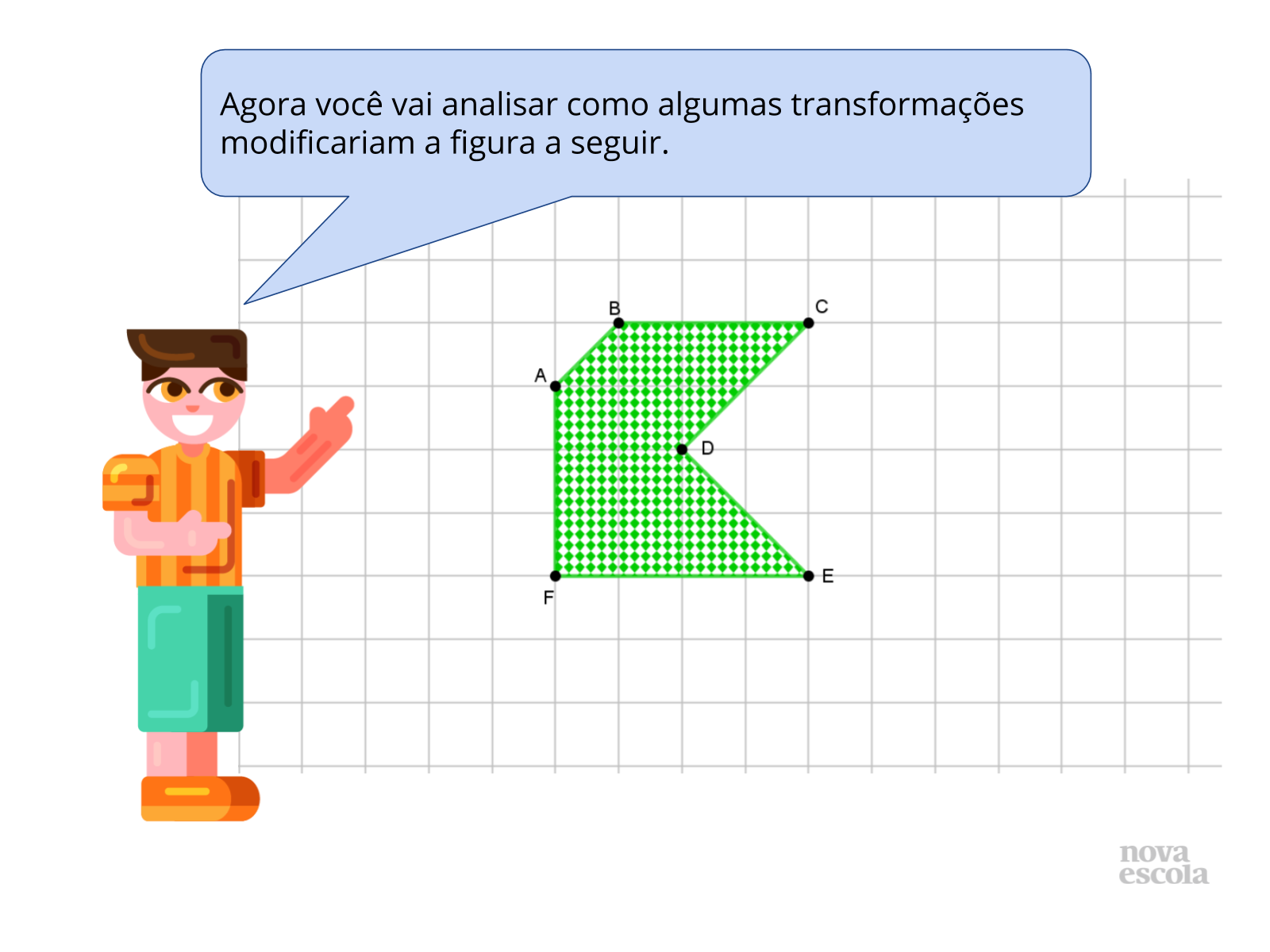
Tempo sugerido: 5 minutos (slides 24 e 25).
Orientações: Projete a atividade ou entregue cópias para os alunos e peça que, individualmente, leiam o enunciado e a realizem a atividade. Circule pela classe para verificar como os alunos estão realizando a tarefa e, caso algum aluno termine, solicite que ele faça esboços das imagens geradas por estas transformações. O Raio X é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito de equivalências entre composições de transformações.
Materiais complementares para impressão:
Resolução da atividade complementar
Raio X

Tempo sugerido: 5 minutos (slides 24 e 25).
Orientações: Projete a atividade ou entregue cópias para os alunos e peça que, individualmente, leiam o enunciado e a realizem a atividade. Circule pela classe para verificar como os alunos estão realizando a tarefa e, caso algum aluno termine, solicite que ele faça esboços das imagens geradas por estas transformações. O Raio X é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito de equivalências entre composições de transformações.
Materiais complementares para impressão:
Resolução da atividade complementar
Sugestão de adaptação para ensino remoto
Código do plano
MAT8_15GEO04
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS
- Necessários: Papel, lápis, régua, papel quadriculado, WhatsApp
- Opcionais: Messenger Sala de aluno ( https://www.messenger.com/groupcall/LINK:4svjhs7dyZw8zoxm/), Meet, Hangout, Zoom, plataforma da Khan Academy ( https://pt.khanacademy.org/)
Portal OBMEP ( https://portaldaobmep.impa.br/index.php/modulo/lista?serie=3)
Geogebra https://play.google.com/store/apps/details?id=org.geogebra&hl=pt_BR
Para este plano, foque na etapa ATIVIDADE PRINCIPAL
Aquecimento
Você pode usar o Aquecimento juntamente com a Atividade principal, adaptá-lo como exemplo nas orientações ou mesmo suprimi-lo para focar unicamente na Atividade principal.
Atividade principal
O uso do papel quadriculado é importante nessa atividade, especialmente se o aluno não tiver como imprimir. Há 3 itens na atividade. Você pode selecionar alguns ou solicitar que os alunos façam todas as questões. Encaminhe orientações, via áudio ou vídeo (WhatsApp), focando em informações que permitam que os alunos realizem a atividade autonomamente. A linguagem matemática adotada na situação é extremamente importante, por isso, talvez você tenha que retomá-la ou mesmo solicitar que os alunos façam um glossário com exemplos. Sugerimos que você encaminhe a atividade principal (versão impressa) para os alunos realizarem, solicitando que eles deem um retorno da atividade. Mantenha um canal de comunicação para dúvidas e esclarecimentos.
Na plataforma da Khan Academy há vários vídeos e demais recursos que tratam de congruência (link 1) e transformações (link 2). Você pode selecionar os materiais pertinentes e indicar aos alunos que possuem acesso à internet.
https://pt.khanacademy.org/math/geometry/hs-geo-congruence/hs-geo-trans-and-congruence
https://pt.khanacademy.org/math/geometry-home/transformations
No Portal da OBMEP há exploração dos elementos básicos da geometria plana (partes 1, 2 e 3) que pode servir de apoio aos alunos que possuem internet.
https://portaldaobmep.impa.br/index.php/modulo/lista?serie=3
Discussão das soluções
Observe as respostas e dúvidas apresentadas pelos alunos para dar um feedback à turma. Considere, sobretudo, os equívocos e as estratégias adotadas para poder reorientar o estudo e dar dicas a para a realização de novas atividades (Raio X e atividades complementares). Use o WhatsApp e grave um áudio ou vídeo curto para dar um ‘fechamento’ à aula. Se sua turma dispuser de ferramentas e internet, dê preferência por realizar as discussões em tempo real, através de uma das plataformas sugeridas abaixo. Solicite que os alunos realizem as demais atividades propostas neste plano. Mas, não esqueça de manter um canal de comunicação para discussão também dessas novas atividades.
Se for possível discutir em tempo real com sua turma, use o Meet, Hangout ou Zoom e considere apenas os itens e os conceitos de maior relevância.
Você pode usar também o Messenger Sala de aluno https://www.messenger.com/groupcall/LINK:4svjhs7dyZw8zoxm/
Sistematização
xxxx
Encerramento
xxxx
Raio X
Use o Raio X e as atividades complementares como forma de revisão para consolidação das aprendizagens. Não esqueça de retomar discussões também dessas atividades e focar nos pontos de aprendizagem mais críticos.
Convite às famílias
Um dos itens da atividade principal pode ser adaptado para discussão com as famílias, sem a necessidade da linguagem específica matemática. Pessoas não letradas são capazes de analisar e opinar sobre a questão, mesmo que não conheçam os conceitos matemáticos de translação, reflexão e rotação.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Renata Akemi Maekawa
Mentor: Fabricio Eduardo Ferreira
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
(EF08MA15) Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.
Objetivos Específicos
- Analisar como conjuntos de transformações isométricas modificam figuras no plano cartesiano.
- Compreender as características das transformações isométricas e de composições de transformações.
- Verificar equivalência entre conjuntos de transformações com e sem apoio de construções.
Conceito-chave
Composição de transformações isométricas no plano cartesiano
Recursos Necessários
- Lápis, tesoura e fichas impressas.
- Projetor (se possível)