Sugestão de adaptação para ensino remoto
Código do plano
MAT4_19GEO_06
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS
- Necessários: (apenas se forem absolutamente indispensáveis; caso contrário, inserir todos como opcionais)
- Opcionais: Jamboard, Loom, YouTube, Geogebra, e-mail, Google Formulários.
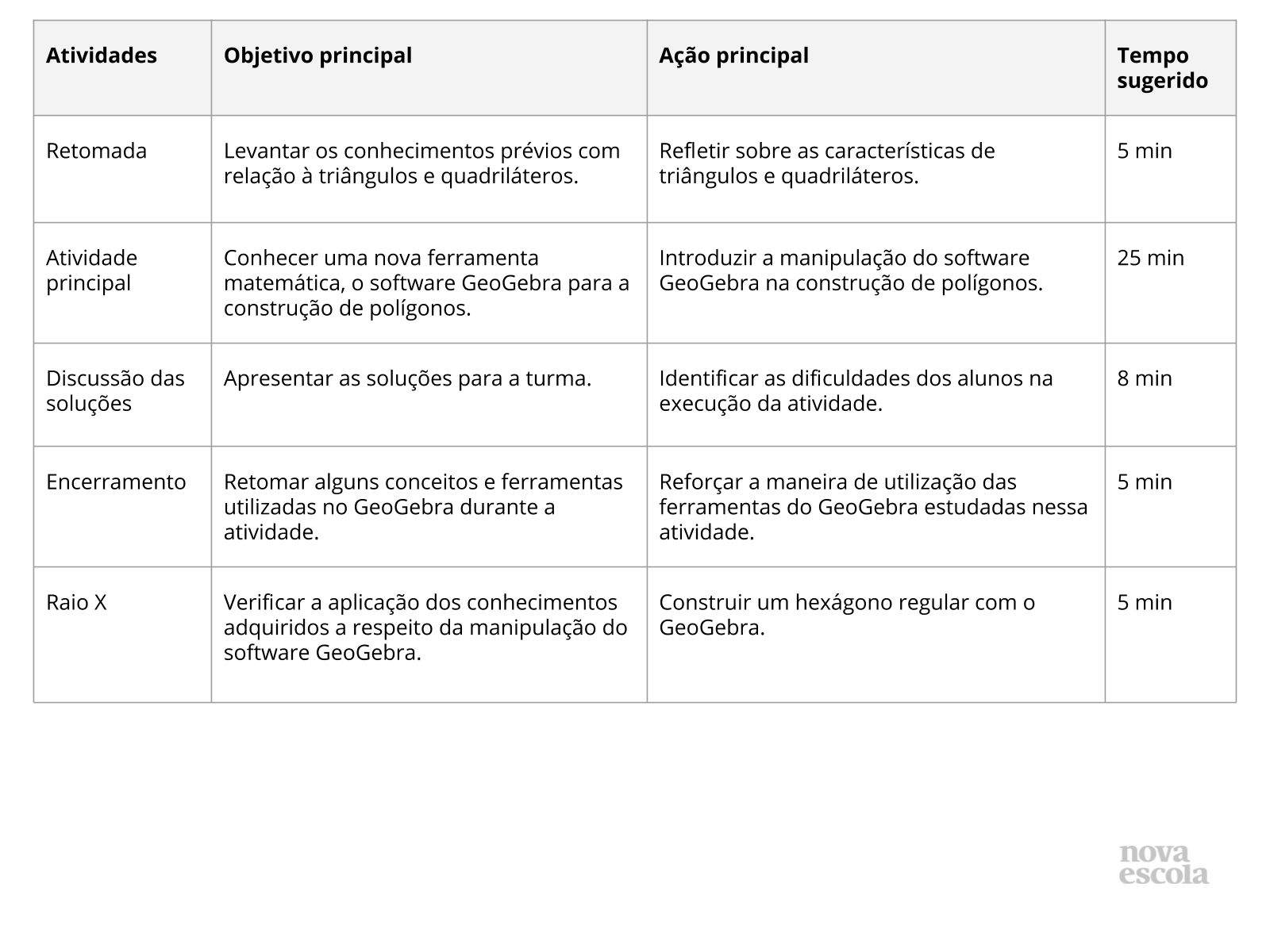
Para este plano, foque na etapa Discussão das Soluções.
Retomada
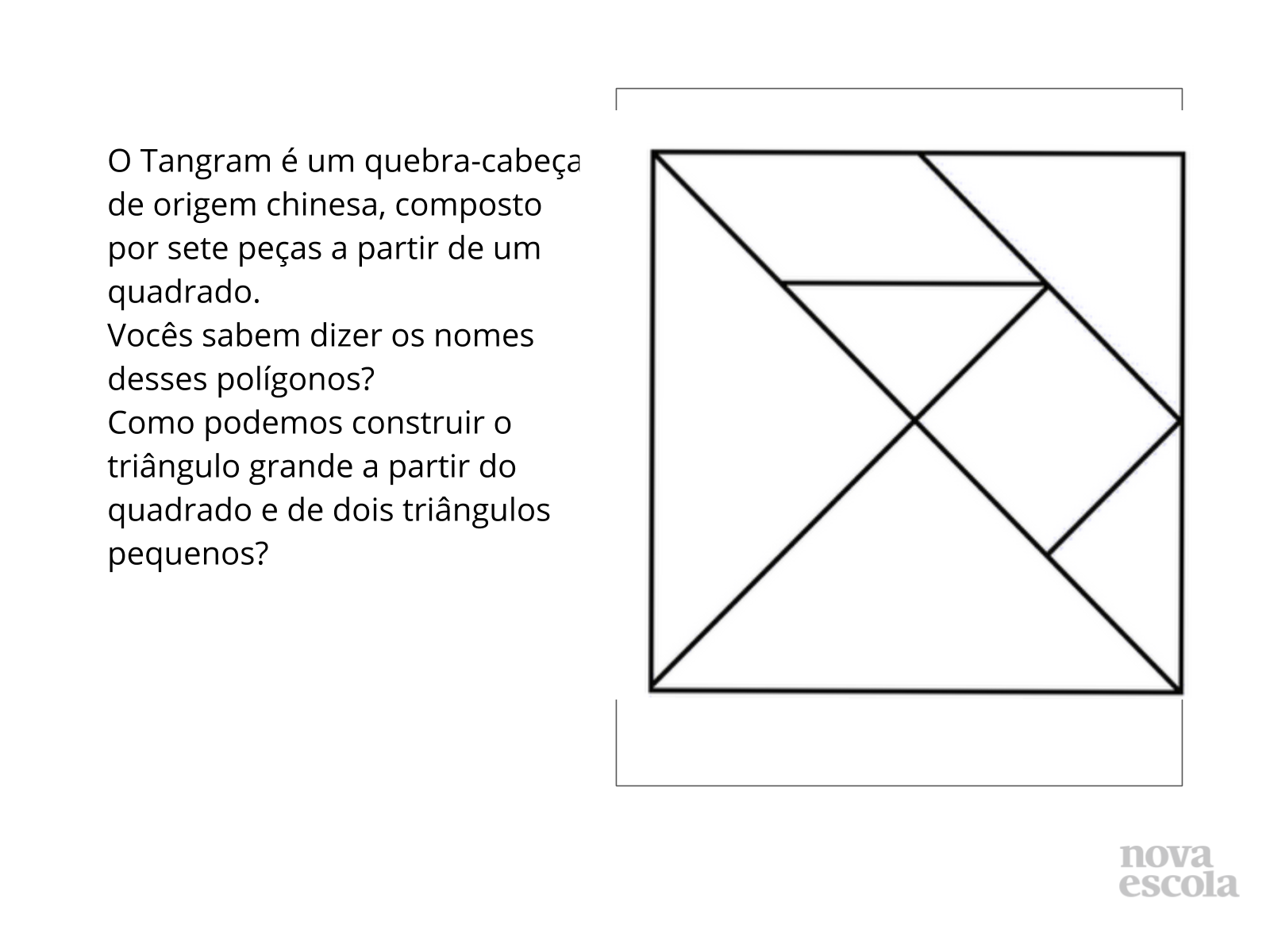
O professor pode pedir que os alunos usem as peças do tangram pelo modelo oferecido em folha impressa ou que utilizem um modelo construído pelo próprio professor usando o Jamboard, para experimentar a montagem de algumas figuras (pesquise modelos para desafiar os alunos a experimentarem um pouco mais esse quebra-cabeça tão rico e cheio de possibilidades).
Atividade principal
Propor que os alunos construam o tangram usando o Geogebra, conforme as instruções presentes nesta etapa. O Geogebra Classic também pode ser encontrado neste link: https://www.geogebra.org/classic
Discussão das soluções
O professor pode gravar um vídeo com o auxílio do Loom, capturando a tela enquanto orienta e dá dicas para o uso do Geogebra por parte dos alunos. Nesse sentido, o próprio professor poderá experimentar a ferramenta e pensar em possíveis dificuldades e necessidades que os alunos apresentem ao produzirem as peças do tangram. O professor pode disponibilizar o vídeo no YouTube, para que a turma consiga acessar e utilizar das dicas no trabalho de construção das peças.
É interessante que o professor possa gravar outro vídeo propondo a reflexão sobre os polígonos que eles utilizaram na construção do tangram e suas propriedades, além das diferenças entre eles.
Sistematização
Não há.
Encerramento
É possível usar o vídeo gravado na etapa de Discussão das Soluções para que os alunos façam o registro no caderno do que aprenderam com esta aula.
Raio X
Propor aos alunos o uso do Geogebra e o envio das construções obtidas ao professor, seja por e-mail ou usando o Google Formulários.
Convite às famílias
Convidar a família a conhecer e explorar junto com o aluno o Geogebra e suas possibilidades de construção.