Resumo da aula
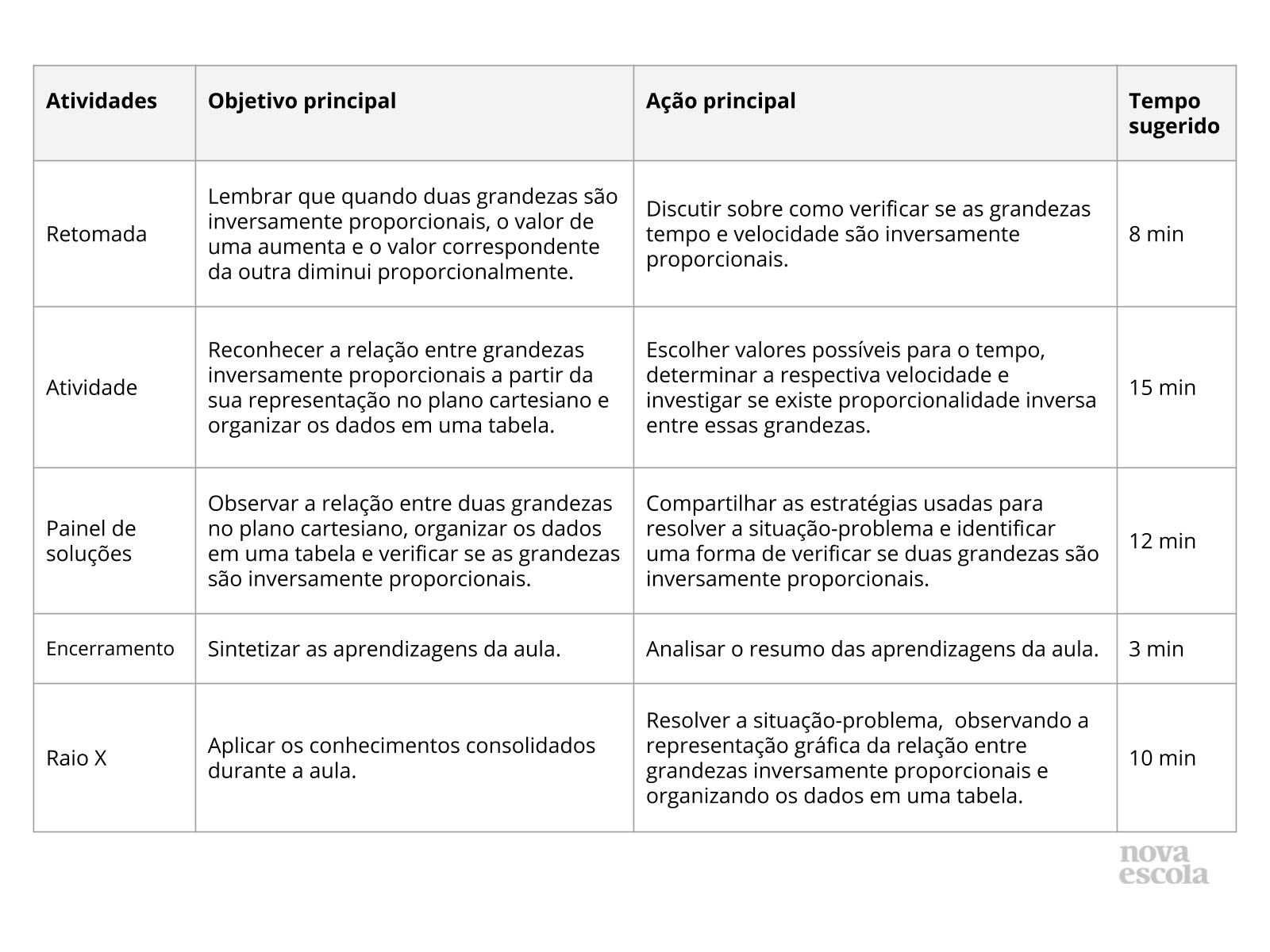
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo sugerido: 8 minutos.
Orientações: Inicie a aula apresentando aos alunos a situação-problema. Esclareça que o tempo está expresso somente em horas, por isso foi utilizada a notação 1,5h ao invés de 1h30min. Pergunte sobre como podemos verificar se as grandezas tempo e velocidade são inversamente proporcionais. Uma forma de fazer essa verificação é calculando a razão entre os valores de uma delas, comparando-a ao inverso da razão entre os valores correspondentes da outra. Como 1,5 : 1 = 93 : 62 (igual a 1,5) e 2 : 1,5 = 62 : 46,5 (igual a 1,333...), vemos que aumentando o valor de uma grandeza, o valor da outra diminui proporcionalmente e portanto, as grandezas são inversamente proporcionais.
Propósito: Lembrar que quando duas grandezas são inversamente proporcionais, o valor de uma aumenta e o valor correspondente da outra diminui proporcionalmente.
Discuta com a turma:
- Atribuindo outro valor para o tempo, como podemos calcular a respectiva velocidade?
Atividade principal
Tempo sugerido: 15 minutos (Slides 4 e 5).
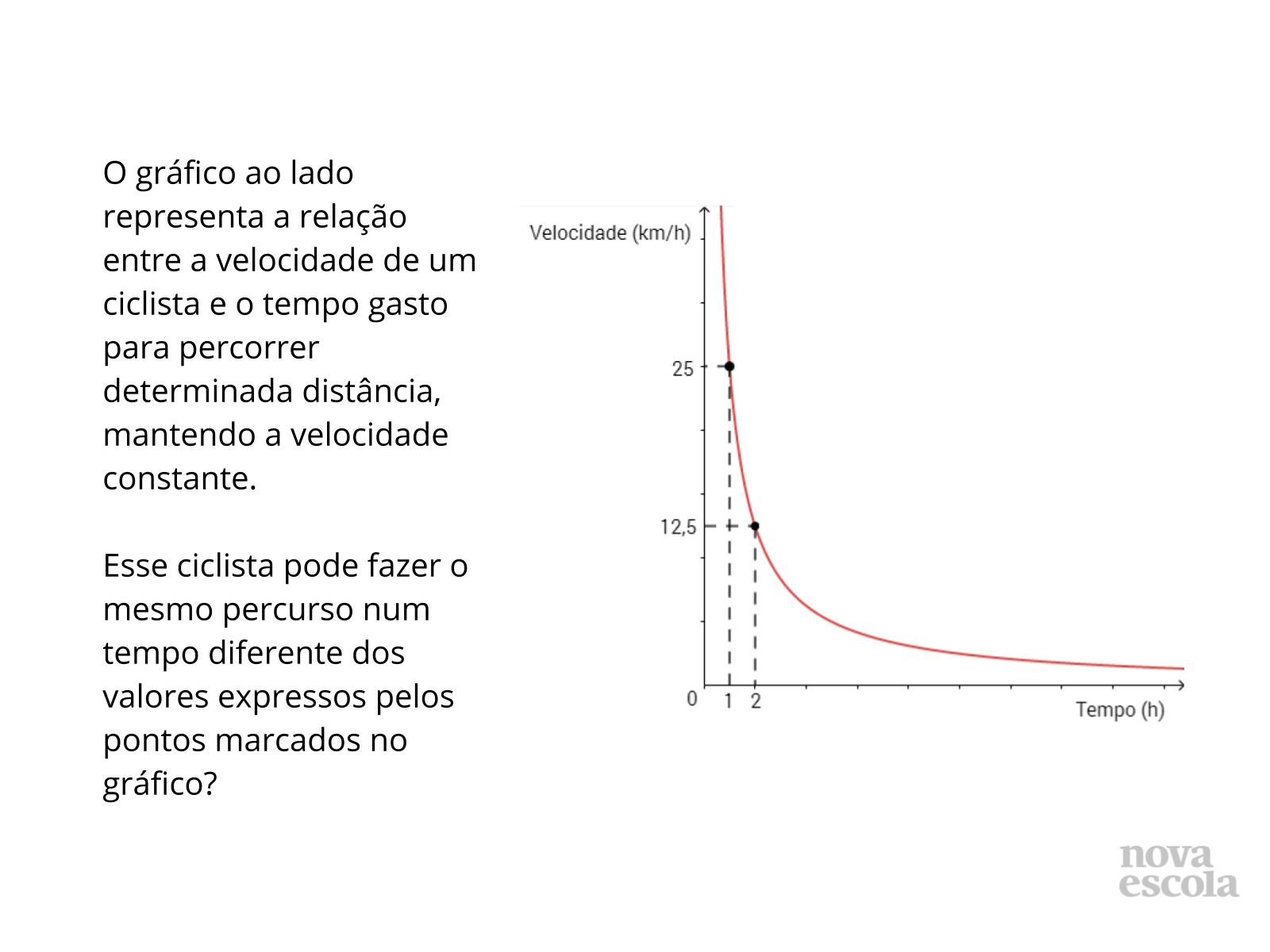
Orientações: Peça que, individualmente, os alunos leiam a atividade, analise o gráfico e responda a questão do slide 4. Aguarde alguns minutos e solicite que construam a tabela e respondam ao questionamento do slide 5. Em seguida, deixe que discutam com um colega suas soluções e modos de resolver a atividade. Reserve um tempo para um debate coletivo e peça que as duplas compartilhem o que discutiram.
Propósito: Perceber a relação entre as grandezas inversamente proporcionais a partir da sua representação gráfica, no plano cartesiano, e representar essa relação organizando os dados em uma tabela.
Discuta com a turma:
- Como podemos determinar a velocidade do ciclista, sabendo o tempo gasto no percurso?
- Como podemos saber se as grandezas velocidade e tempo são inversamente proporcionais?
Materiais complementares:
Atividade principal
Resolução atividade principal
Guia de intervenção
Atividade principal

Tempo sugerido: 15 minutos (Slides 4 e 5).
Orientações: Peça que, individualmente, os alunos leiam a atividade, analise o gráfico e responda a questão do slide 4. Aguarde alguns minutos e solicite que construam a tabela e respondam ao questionamento do slide 5. Em seguida, deixe que discutam com um colega suas soluções e modos de resolver a atividade. Reserve um tempo para um debate coletivo e peça que as duplas compartilhem o que discutiram.
Propósito: Perceber a relação entre as grandezas inversamente proporcionais a partir da sua representação gráfica, no plano cartesiano, e representar essa relação organizando os dados em uma tabela.
Discuta com a turma:
- Como podemos determinar a velocidade do ciclista, sabendo o tempo gasto no percurso?
- Como podemos saber se as grandezas velocidade e tempo são inversamente proporcionais?
Discussão da solução
Tempo sugerido: 12 minutos (Slides 6 a 9).
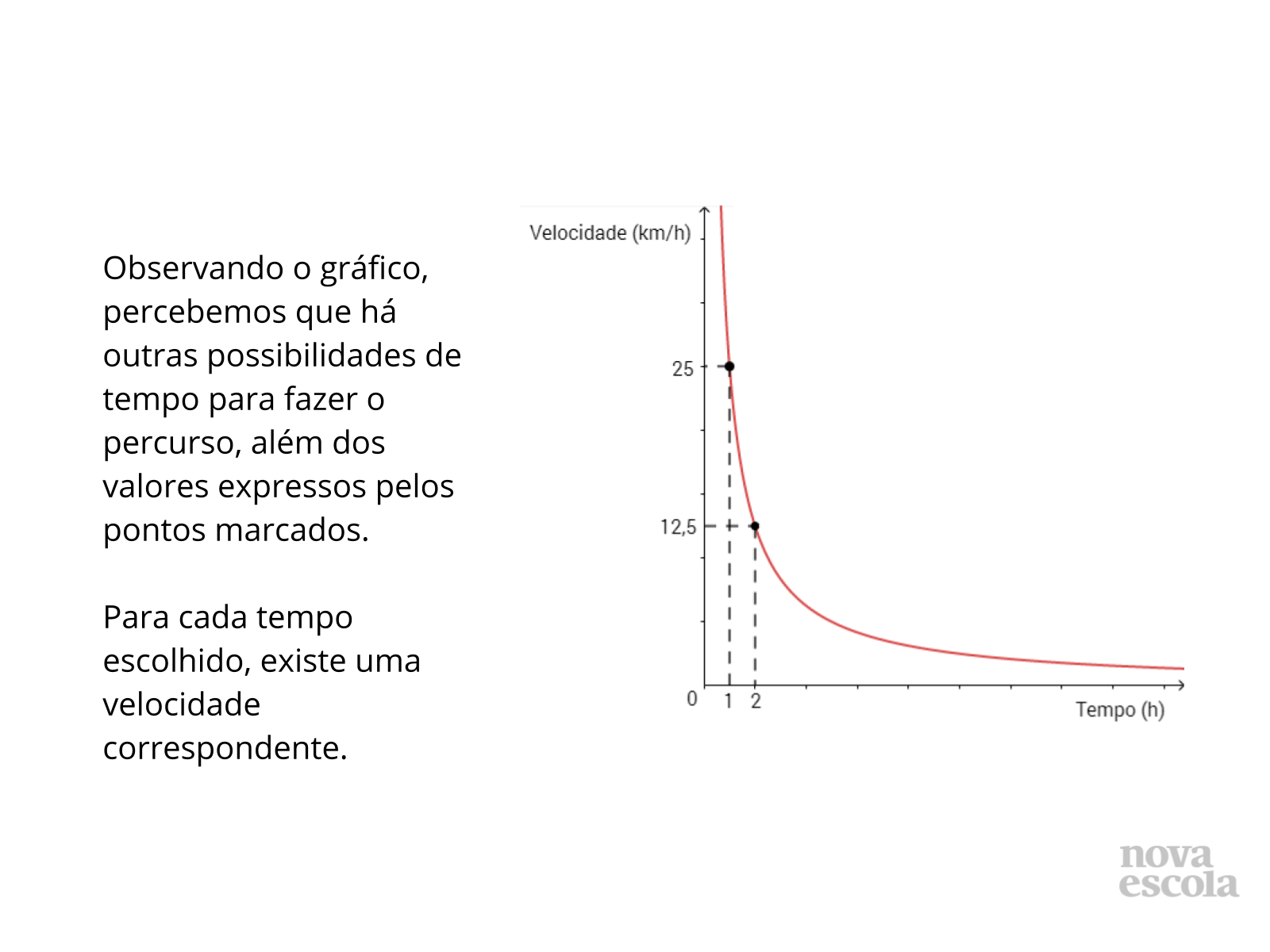
Orientações: Depois que os alunos compartilharem as estratégias deles, peça que observem que diferentes estratégias podem ser utilizadas para resolver o problema. Apresente a proposta, acima, para determinar outros valores para a velocidade a partir do tempo escolhido, com base nos valores apresentados no gráfico.
Propósito: Fazer uma síntese das ideias discutidas até o momento.
Discuta com a turma:
- Escolhendo um valor para o tempo, como podemos calcular a velocidade correspondente?
- O que ocorre com o valor da velocidade, se o tempo escolhido for muito grande? E se o tempo for muito pequeno?
- Há uma constante de proporcionalidade envolvida nessa situação-problema?
Discussão da solução
Tempo sugerido: 12 minutos (Slides 6 a 9).
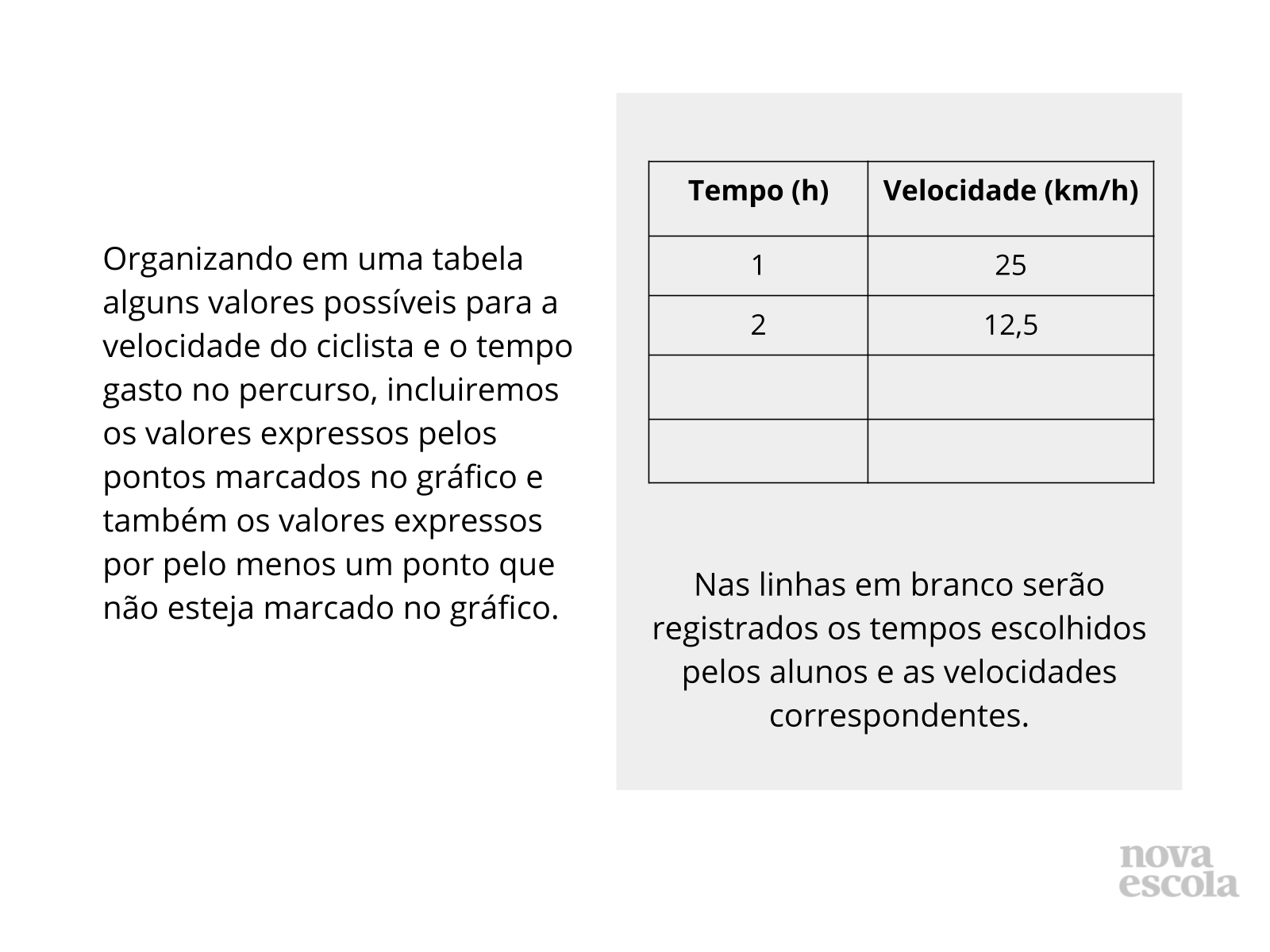
Orientações: Depois que os alunos compartilharem as estratégias deles, peça que observem que diferentes estratégias podem ser utilizadas para resolver o problema. Apresente a proposta, acima, para determinar outros valores para a velocidade a partir do tempo escolhido, com base nos valores apresentados no gráfico.
Propósito: Fazer uma síntese das ideias discutidas até o momento.
Discuta com a turma:
- Escolhendo um valor para o tempo, como podemos calcular a velocidade correspondente?
- O que ocorre com o valor da velocidade, se o tempo escolhido for muito grande? E se o tempo for muito pequeno?
- Há uma constante de proporcionalidade envolvida nessa situação-problema?
Discussão da solução

Tempo sugerido: 12 minutos (Slides 6 a 9).
Orientações: Depois que os alunos compartilharem as estratégias deles, peça que observem que diferentes estratégias podem ser utilizadas para resolver o problema. Apresente a proposta, acima, para determinar outros valores para a velocidade a partir do tempo escolhido, com base nos valores apresentados no gráfico.
Propósito: Fazer uma síntese das ideias discutidas até o momento.
Discuta com a turma:
- Escolhendo um valor para o tempo, como podemos calcular a velocidade correspondente?
- O que ocorre com o valor da velocidade, se o tempo escolhido for muito grande? E se o tempo for muito pequeno?
- Há uma constante de proporcionalidade envolvida nessa situação-problema?
Discussão da solução

Tempo sugerido: 12 minutos (Slides 6 a 9).
Orientações: Depois que os alunos compartilharem as estratégias deles, peça que observem que diferentes estratégias podem ser utilizadas para resolver o problema. Apresente a proposta, acima, para determinar outros valores para a velocidade a partir do tempo escolhido, com base nos valores apresentados no gráfico.
Propósito: Fazer uma síntese das ideias discutidas até o momento.
Discuta com a turma:
- Escolhendo um valor para o tempo, como podemos calcular a velocidade correspondente?
- O que ocorre com o valor da velocidade, se o tempo escolhido for muito grande? E se o tempo for muito pequeno?
- Há uma constante de proporcionalidade envolvida nessa situação-problema?
Encerramento
Tempo sugerido: 3 minutos.
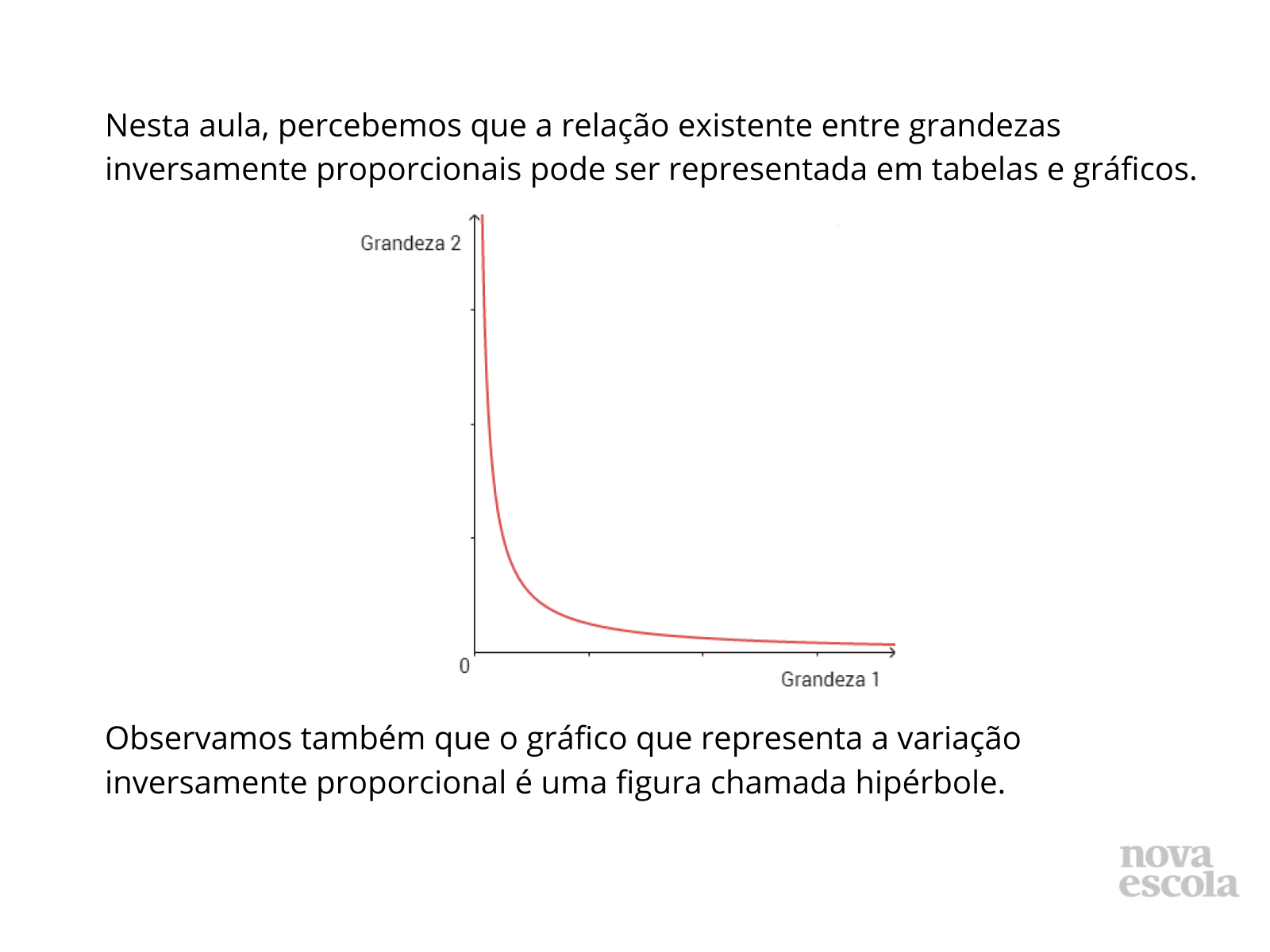
Orientações: Destaque para os alunos que a relação existente entre grandezas inversamente proporcionais pode ser representada em tabelas e gráficos.
Propósito: Sintetizar as aprendizagens da aula.
Raio X
Tempo sugerido: 10 minutos (Slides 11 e 12).
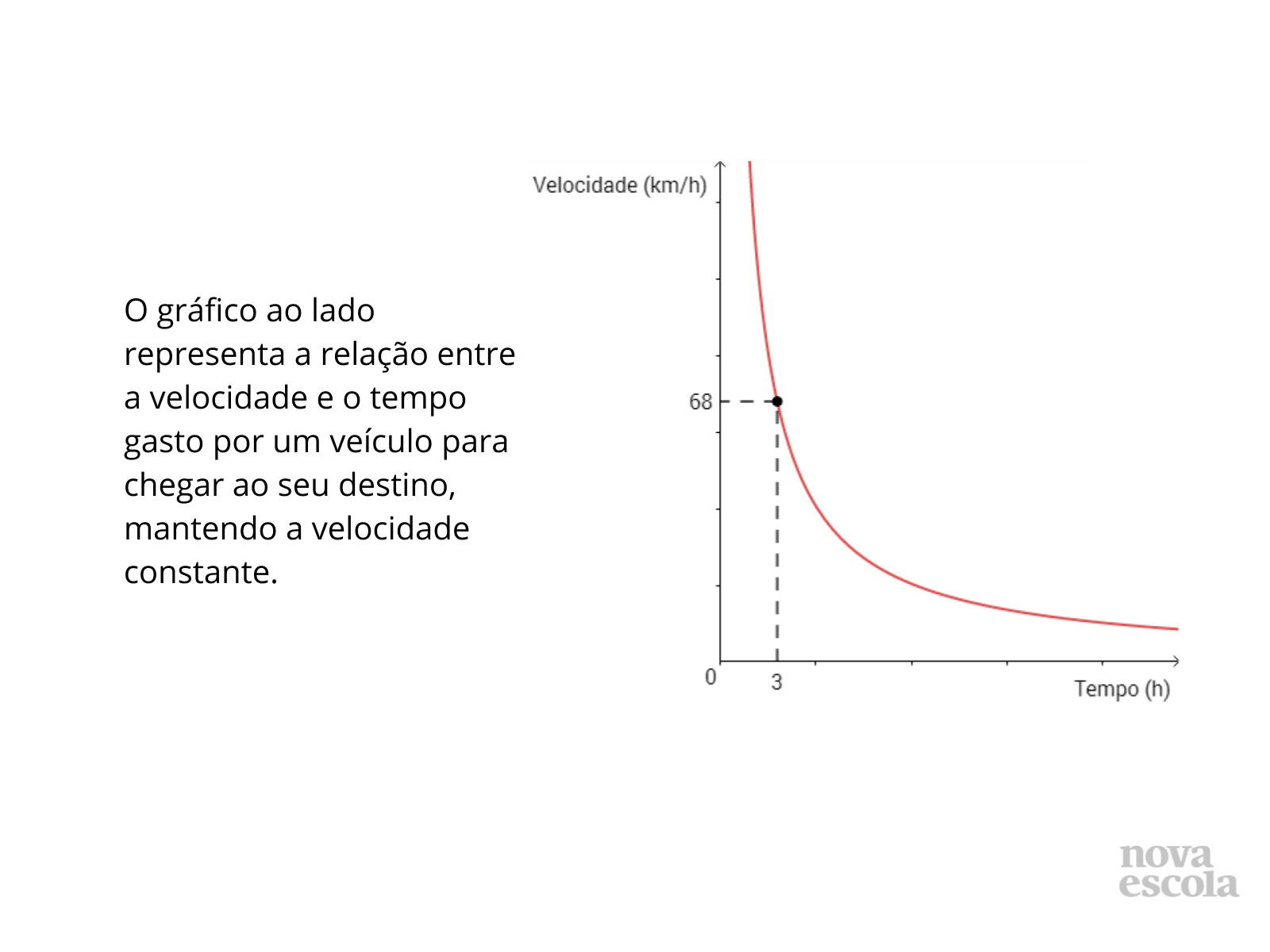
Orientações: Peça que, individualmente, os alunos leiam e realizem a atividade. Circule para verificar como os alunos estão resolvendo. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando as soluções no quadro.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito da representação gráfica da relação entre grandezas inversamente proporcionais e da organização desses dados em tabelas.
Discuta com a turma:
- Como podemos determinar o número de horas necessárias para manter outras velocidades, além do valor expresso pelo ponto marcado no gráfico?
- A velocidade do veículo e o tempo gasto são grandezas inversamente proporcionais?
Materiais complementares:
Atividade raio x
Atividade complementar
Resolução raio x
Resolução atividade complementar
Raio X

Tempo sugerido: 10 minutos (Slides 11 e 12).
Orientações: Peça que, individualmente, os alunos leiam e realizem a atividade. Circule para verificar como os alunos estão resolvendo. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando as soluções no quadro.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito da representação gráfica da relação entre grandezas inversamente proporcionais e da organização desses dados em tabelas.
Discuta com a turma:
- Como podemos determinar o número de horas necessárias para manter outras velocidades, além do valor expresso pelo ponto marcado no gráfico?
- A velocidade do veículo e o tempo gasto são grandezas inversamente proporcionais?
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. 
























