Guia de intervenções
Plano de Aula
Plano de aula: Qual o peso ideal para sua mochila?
Plano 5 de uma sequência de 10 planos. Veja todos os planos sobre Grandezas e Medidas
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Rosélia Sezerino Fenner
Mentor: Fabio Menezes da Silva
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF05 MA19) Resolver e elaborar problemas envolvendo medidas das grandezas comprimento, área, massa, tempo, temperatura e capacidade, recorrendo a transformações entre as unidades mais usuais em contextos socioculturais.
Objetivos específicos
Estimar, identificar e relacionar unidades padronizadas de medidas de massa, envolvendo situações-problemas.
Conceito-chave
Medidas de massa
Recursos necessários
- Balança para pesagem dos alunos (pode ser do tipo mecânica antropométrica).
- Se possível, diversos modelos de balanças (de precisão, de dois pratos, de precisão de bolso, eletrônica neonatal, balança digital, entre outras que conseguir.
- Embalagens de alimentos : 4 embalagens de 250 g (café, margarina... ), 2 com 500 g (fubá, margarina, macarrão ...), 1 embalagem com 1 kg (açúcar, margarina, farinha, etc)
- Lápis, borracha, caderno.
- Dicionário.
- Atividade impressa ou não para colar no caderno.
Habilidades BNCC:
Objetivos de aprendizagem
Estimar, identificar e relacionar unidades padronizadas de medidas de massa, envolvendo situações-problemas.
Resumo da aula
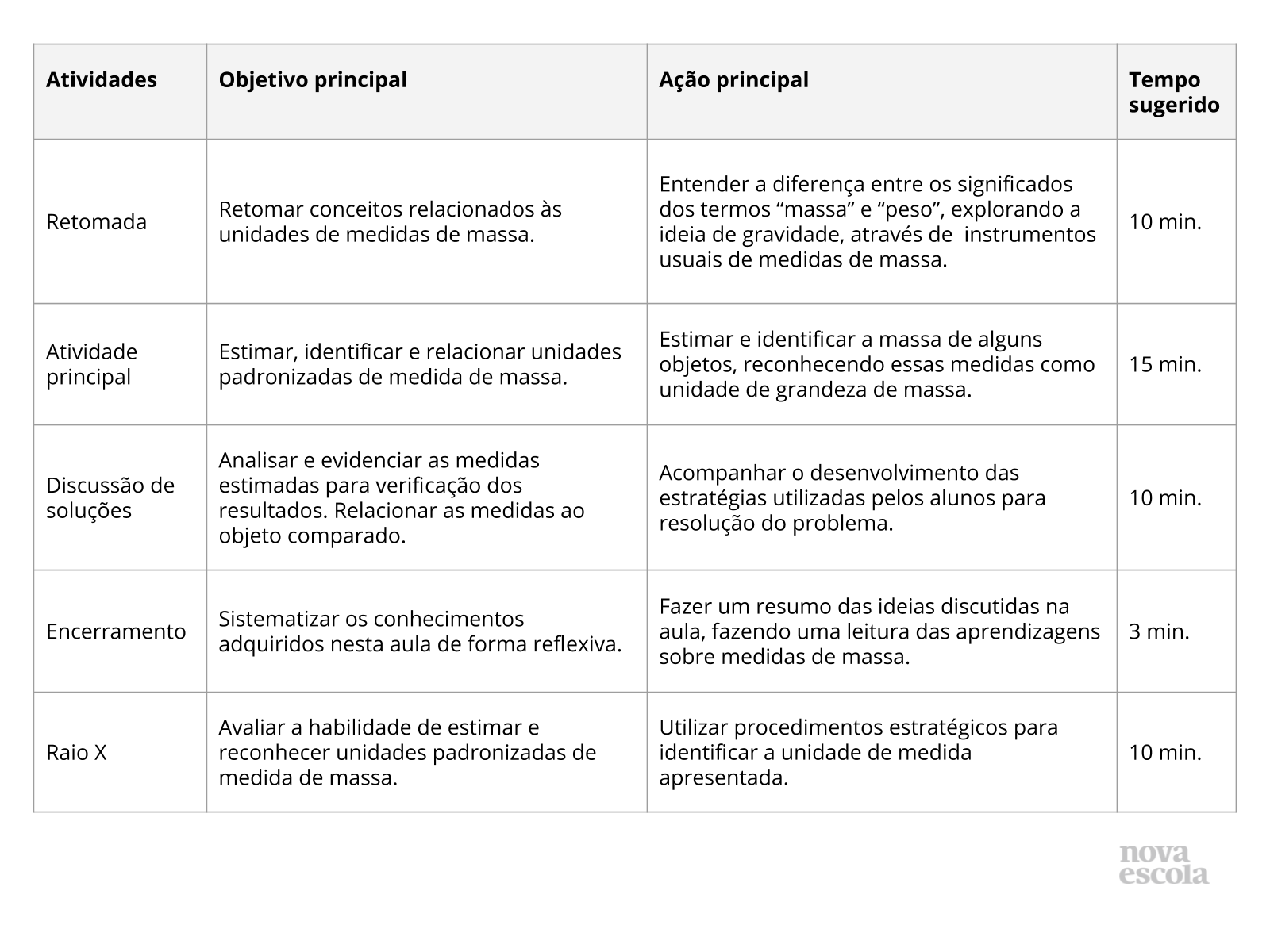 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para turma.
Propósito: Compartilhar com a turma o objetivo da aula.
Retomada

Tempo sugerido: 10 minutos (slides 3 e 4).
Orientação: Retome com os alunos noções sobre massa, enfatizando principalmente que a linguagem popular de alguns conceitos nem sempre está adequado ao rigor científico. É comum ouvirmos no dia a dia frase como “ Este queijo pesa um quilograma “. Estas expressões são utilizadas no cotidiano das pessoas, mas não são cientificamente corretas. Por mais estranho que pareça você ouvir alguém dizer “ Quantos kg você tem de massa? “, essa seria a forma cientificamente correta, porém, pouco entendida pelas pessoas.
Massa e peso são grandezas físicas diferentes, portanto, é preciso levar o aluno a compreender que é do senso comum, usar a palavra peso no lugar de massa, podendo assim, utilizar essa expressão, porém, tendo clareza do significado dos dois termos.
Para entendimento da diferença entre massa e peso, o aluno precisa apropriar-se da ideia de gravidade, pois embora peso e massa sejam conceitos diferentes, seus significados estão relacionados pela gravidade.
Esse é um assunto que poderá ser explorado de forma mais aprofundada nas aulas de Ciências, realizando experiências significativas antes de aplicar esta aula.
Peça a cada um dos alunos que pesquisem no dicionário o significado de peso e massa. No dicionário, há vários significados principalmente da palavra massa, porém, oriente-os a usar o significado que melhor se relaciona à medida. Discuta com eles as informações encontradas, peça que registrem as conclusões e na sequência, faça a seguinte reflexão:
A Terra exerce uma força gravitacional “ puxando “ corpos para si e essa força é chamada peso. Quando eu pergunto “Qual é o seu peso?”, na verdade, quero saber quanto de matéria tem em seu corpo, ou seja, qual é a sua massa. Portanto, massa é a quantidade de matéria presente em um corpo e pode ser medida em uma balança, ela é a mesma em qualquer lugar. Já o peso, é a relação entre a massa de um corpo e a gravidade do lugar onde está. Considerando que a força gravitacional na Terra e na Lua são diferentes, que, quanto maior a massa de um corpo maior será sua atração, e que a massa da Terra é bem maior que a massa da Lua, o corpo de uma pessoa é mais atraído pela superfície da Terra do que pela superfície da Lua. Na Terra, o peso de um corpo é 10 vezes o valor da massa.
Para ilustrar melhor essa colocação reflita com os alunos o seguinte exemplo: Uma pessoa que tem 70 kg de massa corporal (ossos, músculos, pele, órgãos, etc), anda na Terra mantendo-o em pé, em virtude de seu peso. Na Lua, com essa mesma quantidade de massa ( 70 kg ) ele praticamente flutua, pois a aceleração da gravidade de lá em relação à Terra é bem menor e isso afeta o peso do corpo atraído por ela. Assim, é possível concluir que a massa é a mesma em qualquer lugar, enquanto que o peso depende do local onde este corpo está. A relação entre peso e massa é proporcional, ou seja, quanto maior a massa, maior será o peso, portanto, são grandezas proporcionais.
Toda essa reflexão leva o aluno a perceber a relação que existe entre o que ele ouve no seu dia a dia e o que é explicado pela ciência. Quando apropriado o significado, é possível usar o termo peso nas atividades relacionadas à construção do conceito de massa, pois ele saberá distinguir um do outro.
Como sugestão de pesquisa para o professor sobre Grandezas e Medidas, consulte a seguinte fonte: FONSECA, M.C.F.R. (Org). Letramento no Brasil: habilidades matemáticas. São Paulo: Global/Ação Educativa/Instituto Paulo Montenegro, 2004.
Propósito: Levar o aluno a perceber a relação que existe entre os termos peso e massa e seu significado.
Discuta com a turma:
- Em que situações do dia a dia de vocês já ouviram ou usaram os termos peso e massa?
- Qual a diferença entre o significado destes dois termos?
- De acordo com o significado de peso e massa, qual das crianças utilizou o termo correto para expressar-se?
Retomada
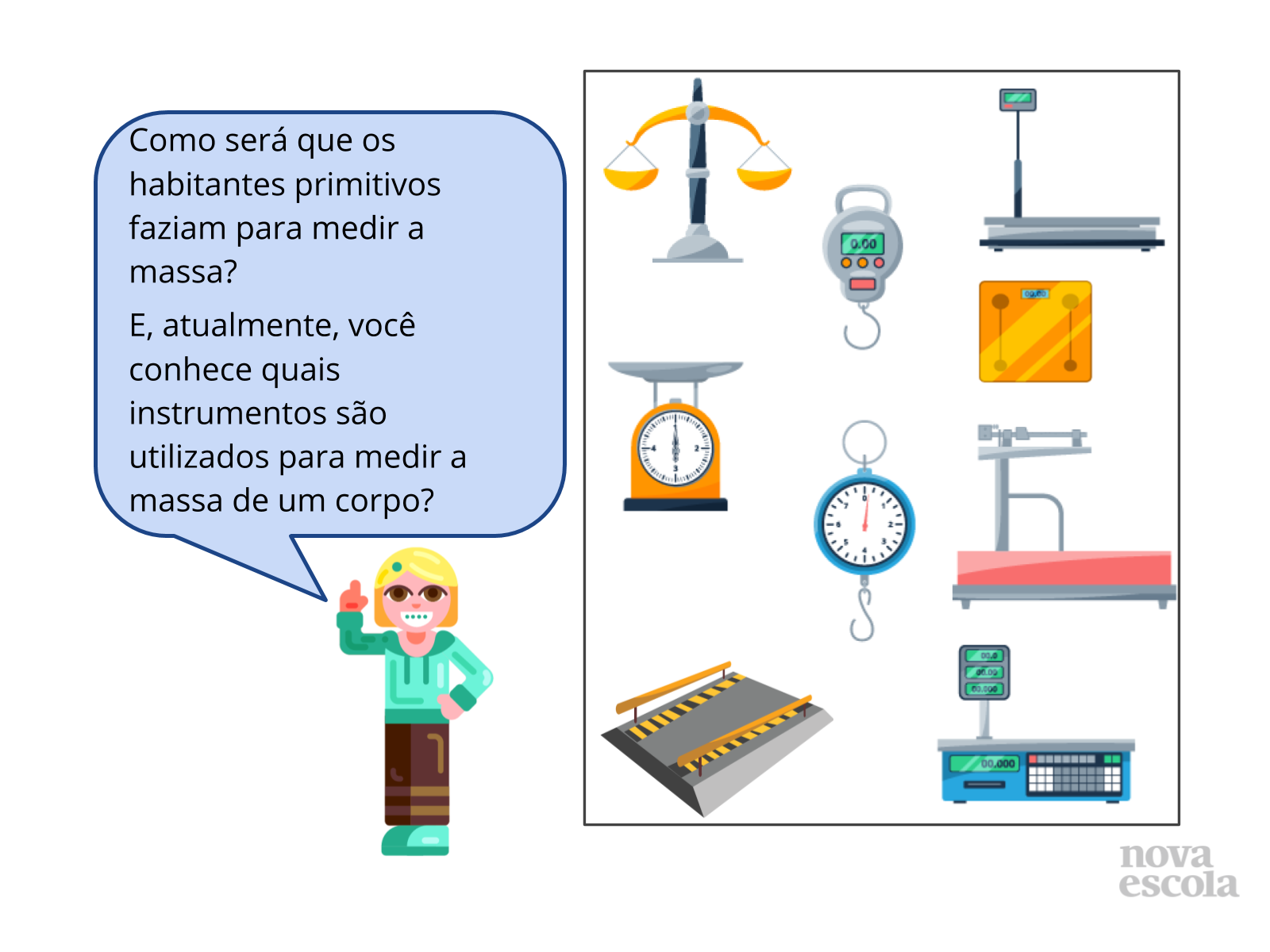
Tempo sugerido: 10 minutos.
Orientação: Providencie, se possível, algumas balanças de diferentes tipos e usos (eletrônica, balança de precisão, balança de dois pratos, etc.). Caso não seja possível o acesso a algum tipo de balança, pode ser construída uma para comparar a massa de alguns objetos, veja aqui como construir uma, ou então, utilize as imagens do slide para que os alunos possam reconhecer alguns desses instrumentos utilizados para medir massa.
Com a compreensão do significado de peso e massa, peça aos alunos para descreverem quais os tipos de balanças usados atualmente que eles conhecem e o que pode ser medido em cada uma (biomédico - pesagem de pessoas em clínicas e hospitais; farmacêutico - pesagem de medicamentos; comercial - alimentos vendidos em supermercados; industrial - pesagem de bens em maior escala como cargas de caminhões).
Nesta descrição, deve-se observar que em alguns tipos de balanças as massas dos corpos são medidas através da força que esses corpos exercem sobre elas (balanças de farmácia, por exemplo). Elas são aferidas pelo fabricante com massas conhecidas. Já na balança de dois pratos, para determinar a massa do corpo, é colocado num prato o que vai ser medido e no outro, um ou mais corpos de massas conhecidas até ficarem em equilíbrio na horizontal. Nesse tipo de balança é feita a comparação de massa.
Para saber mais sobre alguns tipos de balança e seu funcionamento, acesse aqui e saiba mais informações sobre o assunto. Outra sugestão para obter mais informações sobre tipos de balanças e um pouco sobre o histórico desse instrumento de medida, acesse aqui
Após o registro dos alunos, determine um tempo para discussão das ideias do alunos, peça que revelem suas observações, analise as colocações, questione-os, de forma que todos tenham oportunidade de expôr suas opiniões.
Com estes conhecimentos ampliados, pegue dois objetos diferentes, por exemplo, um livro e um caderno, um em cada mão e pergunte aos alunos o que “pesa” mais, o livro ou o caderno? Qual será o “peso” de cada um? Oriente-os a registrar as estimativas no caderno, estimar reduz a incidência de erros ao calcular. Ainda usando as mãos, peça que estimem, o que tem mais massa, o livro de Matemática ou o livro de Português? O lápis, ou o apontador? Imaginem um carro e uma bicicleta, qual tem a maior massa?
Essas comparações têm como objetivo fazer com que os alunos observem que usando as mãos como instrumento de medida, fica mais difícil de fazer estimativas de objetos com massa de valores próximos. Por isso, a necessidade de se criar instrumentos de medidas padronizados e que pudessem fornecer medidas mais precisas. Através dessas comparações o aluno irá descobrir como os povos primitivos faziam para medir a massa de um corpo, usando seu próprio corpo como instrumento de medida. Fonte de pesquisa .
Para encerrar esta primeira etapa, questione os alunos sobre qual a unidade de medida mais indicada para indicar a massa de um cachorro de raça grande, adulto. E a de um passarinho? E de um caminhão? E de um comprimido? Através destas reflexões espera-se que o aluno possa identificar e relacionar unidades padronizadas de medida de massa ( quilograma, o grama, miligrama e a tonelada).
Durante a discussão, chame a atenção dos alunos para o gênero da palavra “ grama “, quando relacionada à unidade de medida de massa, nesta situação o correto é “ o grama “ .
Durante a socialização dos questionamentos, liste no quadro as informações dadas para cada unidade de medida de massa.
Propósito: Identificar instrumentos de medidas de massa, comparar relacionar unidades padronizadas de medidas de massa.
Discuta com a turma:
- Por que o homem precisou medir?
- Quais razões levaram o homem a inventar instrumentos de medidas padronizados?
- Qual o tipo de balança que usaríamos para medir a massa de carne de 1 kg?
- E para calcular a sua massa corporal, qual instrumento mais adequado para fazer essa medição?
- É possível calcular a massa de um comprimido em uma balança do tipo industrial, por quê?
Atividade principal

Tempo sugerido: 15 minutos.
Orientação: Providencie uma balança que seja adequada para verificar o “peso” da mochila e o “peso” de cada aluno, a fim de averiguar se as mochilas estão com “peso” ideal ou não. Ressalta-se aqui que, nem todos os alunos possuem mochila para transportarem o material escolar, por isso, o professor poderá adequar o objeto mochila à uma bolsa ou outro que seja utilizado pelo aluno.
Divida a turma em duplas e distribua para cada aluno uma cópia da atividade proposta. Peça para que a leiam e estimem qual o peso de suas mochilas. Oriente para que anotem no caderno suas previsões. Observe se as previsões são consideradas razoáveis a partir da apresentação de um objeto cuja massa é conhecida. O assunto abordado na atividade é de extrema relevância, por se tratar da saúde física das crianças e adolescentes. Uma discussão maior sobre o tema pode ser tratado de forma interdisciplinar, na disciplina de Ciências ( Temas transversais - Saúde ), podendo trazer para escola um profissional (fisioterapeuta), para falar sobre as consequências que o excesso de peso nas mochilas podem causar para o saúde dos alunos. Mais informações sobre o assunto, acesse aqui.
Medidas estimadas e anotadas, oriente para que em duplas, discutam entre si qual a estratégia que usarão para responder o que se pede. Espera-se que concluam que terão de primeiro pesar as mochilas e também a sua massa corporal para então, saberem se o “peso” de suas mochilas estão de acordo com o recomendado, 10% do “peso” da criança.
Disponibilize a balança para que em duplas façam a verificação das medidas estimadas do “peso” das mochilas. Para melhor organização das informações, distribua também a tabela para que preencham as conclusões obtidas. A tabela poderá ser feita no caderno, conforme modelo no slide a seguir. Acompanhe tudo de perto, observando se os alunos apresentam dificuldade em identificar o “peso” na balança, bem como fazer o registro da medida identificada. Pode ser sugerido para o aluno arredondar as medidas obtidas com duas casas decimais depois da vírgula, ( centésimos) por exemplo: 2, 75 kg para 2, 7 kg, facilitando assim o cálculo da porcentagem logo em seguida.
Ao concluírem essa etapa, socialize as informações, anotando no quadro as medidas estimadas, bem como as verificadas após pesar as mochilas. Observe se as previsões feitas pelos alunos correspondem aos resultados encontrados.
Passe para outra etapa da atividade - medir a massa corporal de cada aluno. Novamente, oriente para que anotem tudo na tabela. De posse das medidas das mochilas e da massa corporal de cada aluno, passe para a etapa seguinte.
Agora, é preciso saber quanto equivale 10% do peso de cada criança. Para isso, é preciso que os alunos já tenham desenvolvido noções de porcentagem. 10% corresponde a um décimo de 100%, ou, 10/100, ou seja, se o aluno “ pesa “ 30 kg, o “peso” ideal da mochila será de 3 kg ( 30 kg : 100 x 10 = 3 kg). Disponibilize uma calculadora para cada dupla ou aluno para realizar o cálculo de porcentagem. Este instrumento agiliza os cálculos na resolução de situações-problemas, embora ela não deve ser vista unicamente uma ferramenta para calcular. O tempo ganho permite que os alunos se detenham mais na elaboração e discussão da estratégia de resolução e os leva a uma maior compreensão do algoritmo, bem como dos conceitos de estimativa e aproximação.
Caso haja poucas calculadoras você pode conduzir os trabalhos em turnos, com um grupo de alunos de cada vez.
Durante a realização da atividade, circule pela sala de aula, observe qual a estratégia que estão usando para resolver a situação problema, se apresentam dificuldades em usar a calculadora. As intervenções, se necessárias, devem ser apenas em forma de questionamentos, levando os alunos a refletirem e tirarem suas próprias conclusões, ou ainda, trocando ideias com os colegas, ouvindo a opinião do outro ele poderá refletir sobre o seu posicionamento em relação à resposta do seu colega.
Para concluir, socialize todas as etapas da atividade, anotando tudo no quadro, comparando os resultados, analisando o ponto de vista de cada um. Tome um exemplo de medida para resolver de forma coletiva o cálculo de porcentagem sem o uso da calculadora. Pergunte quem gostaria de vir até o quadro e resolver através de alguma estratégia o cálculo da porcentagem (10%). Peça à ele que explique para a turma como foi que fez. Pergunte ainda se alguém tem uma estratégia diferente que possa explicar para os colegas, permita que exponham outras sugestões de resolução.
Faça uma reflexão sobre a questão do excesso de “peso” nas mochilas, compare, o “peso” da mochila e a massa corporal de cada aluno. Caso estejam em desacordo ao recomendado, quais as consequências que irão sofrer em virtude desse problema e, o que fazer para reduzir o peso das mochilas e evitar problemas futuros. Observe se todos tiveram oportunidade de expôr suas conclusões. Dê oportunidade para que alguns alunos vão até o quadro para compartilharem suas ideias com a turma.
Professor, passe para o slide seguinte somente após socializar as estratégias e resultados obtidos pelos alunos.
Propósito: Explorar estratégias pessoais de medição.
Discuta com a turma:
- Ao analisarem a atividade, qual foi o primeiro passo para respondê-la?
- Como vocês fizeram para chegar no resultado?
- Há outras formas de resolver a atividade?
- Qual a unidade de medida usada para determinar a massa da mochila e a massa corporal de cada um?
- A mochila “pesa” mais ou menos de 1 kg?
- O que é mais leve, a mochila ou o seu corpo?
- Quantos gramas há no “ peso “ de sua mochila?
- O “peso“ de sua mochila corresponde à medida indicada pelos especialistas, ou seja, 10% do seu “peso“?
- A qual outro objeto é possível comparar a massa da sua mochila?
- Quem é o aluno mais pesado da turma? E o mais leve?
- Quem tem a mochila mais pesada? Quanto ela “pesa“ ?
- O que foi possível concluir com essa atividade?
- O que é possível fazer para resolver o problema de quem está com a mochila com “peso” acima do recomendado?
Materiais complementares:
Resolução da Atividade Principal
Discussão da solução
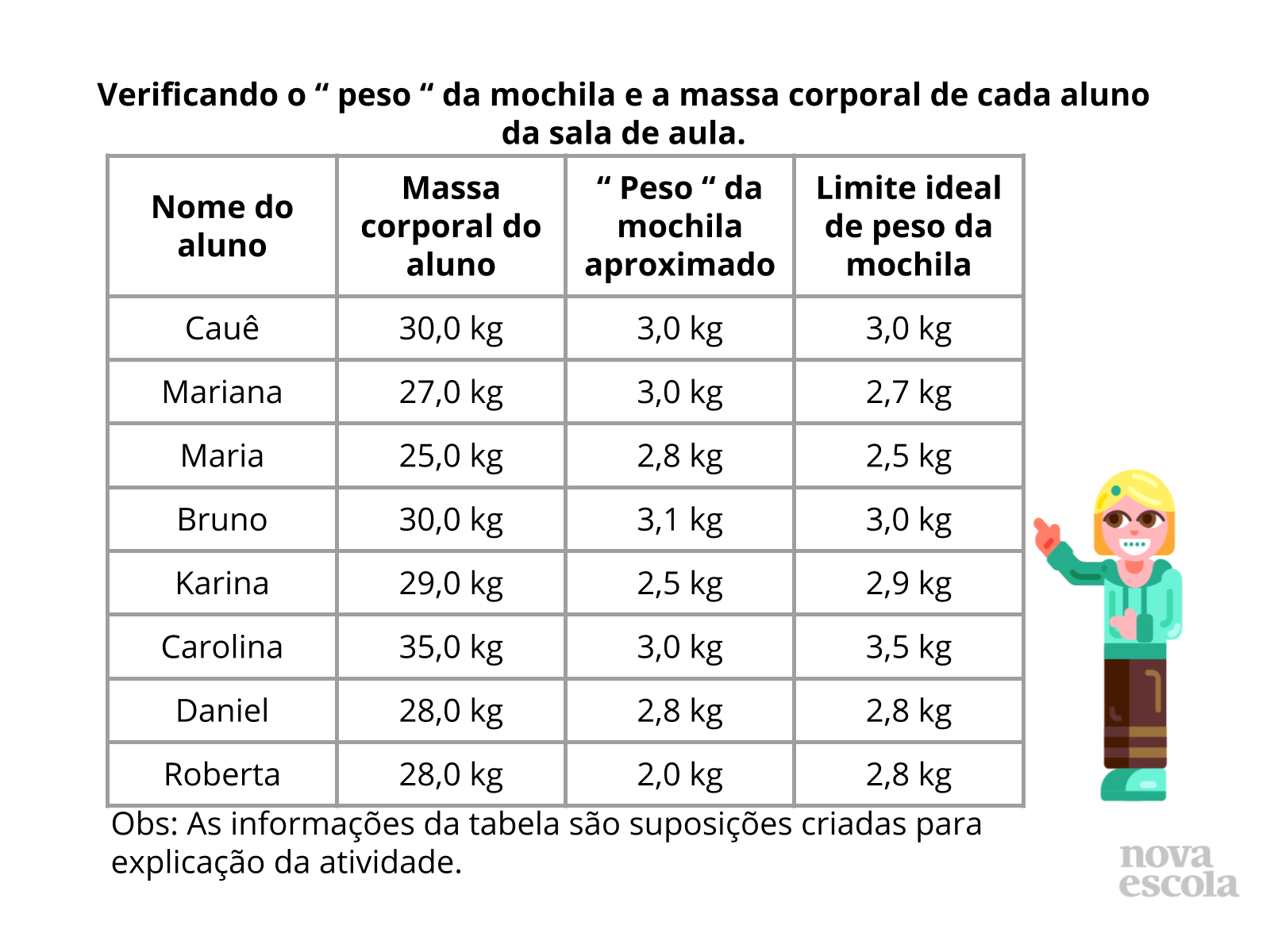
Tempo sugerido: 10 minutos (slides 6 à 10).
Orientação: Depois que os alunos compararam suas estimativas e estratégias de resolução, discuta com a turma as informações da tabela preenchida por eles, bem como os resultados. A tabela do slide é apenas uma demonstração de como deve ser preenchida, o que será discutido com a turma são as informações obtidas por eles durante a pesagem.
Faça uma reflexão, quem está com excesso de peso na mochila, compare as variações de “ pesos” das mochilas, por exemplo: Um aluno pode ser mais leve que outro, porém, sua mochila pode estar mais pesada.
Discuta ainda o uso da vírgula nas medidas, porque ela foi usada e o que representa. A vírgula é utilizada para separar a unidade de medida quilograma da menor, o grama ( que representa uma parte menor que o kg ). Por exemplo: se o “peso” da mochila for
2, 8 kg - está representado nesta medida 2 kg = 2 000 gramas + 800 gramas = 2 800 gramas.
Comente que as unidades de massa mais utilizadas no cotidiano são o quilograma e o grama, porém, há outras unidades que são utilizadas ( tonelada, arroba, miligrama). Neste caso, a medida mais indicada é o kg e a grama para calcular a massa corporal e a mochila.
Propósito: Discutir coletivamente as estratégias e soluções encontradas para a atividade apresentada.
Discuta com a turma:
- Qual foi a estratégia usada para encontrar a solução para atividade?
- Seria possível realizar esta atividade sem o uso da balança? Como vocês fariam?
- Quantas vezes o “ peso “ da mochila de cada um cabem dentro do “ peso “ do aluno?
- Se juntarmos o “ peso “ de todas as mochilas, quantos quilogramas obteremos?
- A mochila de Marina está com excesso de peso. Esse excesso é mais ou menos que 1 kg?
- Quanto representa esse excesso?
- Quanto falta para a mochila de Carolina atingir o limite de “ peso “ da sua mochila?
- Como vocês representariam essa medida?
- O que vocês acham dessa recomendação dos especialistas sobre o peso das mochilas?
- Quem está de acordo com as recomendações sobre o peso da mochila poderia explicar como faz para organizar seu material para vir à escola?
Discussão da solução

Tempo sugerido: 10 minutos (slides 6 à 10).
Orientação: O uso da calculadora pelos alunos é um ótimo recurso, que precisam saber usá-lo por se tratar de um instrumento usado no dia a dia das pessoas.
Embora o cálculo de porcentagem seja realizado na calculadora, é importante que os alunos entendam que a divisão por 100 é necessária, já que porcentagem é a centésima parte de uma grandeza.
Ao dividir 30 kg por 100, teremos como resultado 3 décimos ou, 30 centésimos ou 300 milésimos. Isso corresponde a 300 g. Multiplica-se 300 g por 10, pois esse valor indica quantas vezes 300 g “ cabem “ em 3 000 g ou 3, 0 kg.
Propósito: Discutir coletivamente a solução para o problema utilizando a calculadora.
Discussão da solução

Tempo sugerido: 10 minutos (slides 6 à 10)
Orientação: Ao considerarmos porcentagem como um número racional, ele também pode ser visto como uma fração, ou seja, uma parte ( 10% de 30 kg). Este pode ser um caminho para solução do problema.
Propósito: Realizar um fechamento discutindo as possibilidades de solução para um mesmo problema.
Discussão da solução

Tempo sugerido: 10 minutos (slides 6 à 10).
Orientação: A porcentagem pode ser pensada ainda de outra forma, através da decomposição de uma certa quantidade. Explora-se a ideia de porcentagem em partes de cem, partes de dez. Esse procedimento permite que o aluno resolva a situação sem que ela tenha que seguir uma regra ou fórmula fixa. Ao fazer uso de diversas formas de resolução, através da investigação e do próprio esforço do aluno, a aprendizagem se tornará mais significativa.
Propósito: Realizar um fechamento discutindo as possibilidades de solução para um mesmo problema.
Discussão da solução

Tempo sugerido: 10 minutos (slides 6 à 10).
Orientação: O processo utilizado aqui é uma questão de raciocínio lógico e dedução.
Propósito: Realizar um fechamento discutindo as possibilidades de solução para um mesmo problema.
Encerramento

Tempo sugerido: 3 minutos.
Orientação: Professor, este é o momento de fazer um fechamento da aula, relacionando as unidades de medidas e sua grandeza.
Propósito: Fazer um fechamento das ideias exploradas nesta aula, sistematizando as aprendizagens.
Raio X
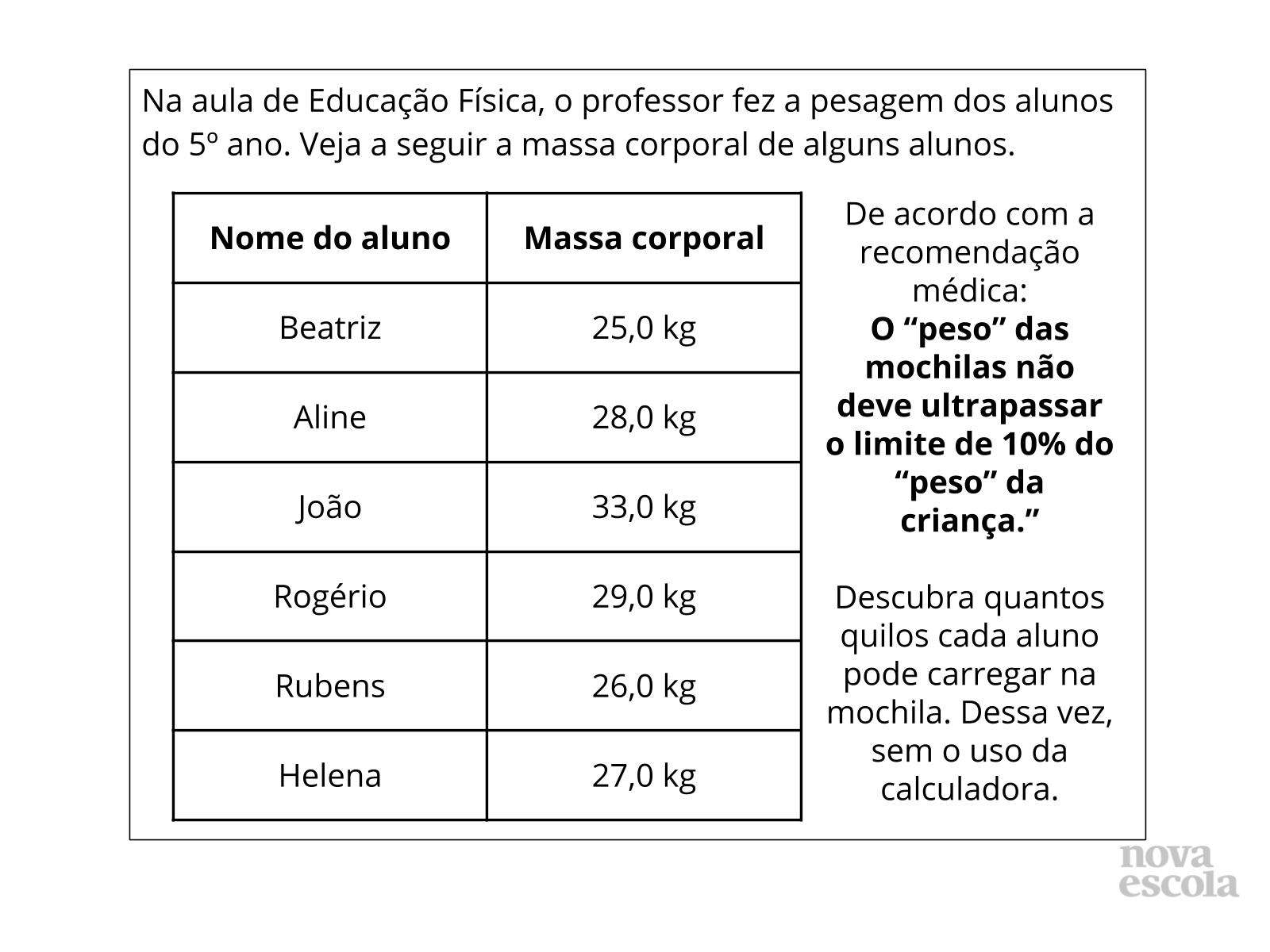
Tempo sugerido: 10 minutos.
Orientação: Peça que individualmente os alunos leiam a atividade proposta, e a realizem utilizando os conhecimentos adquiridos na aula.
O Raio X é o momento de avaliar se os alunos conseguiram identificar grandezas mensuráveis que ocorrem no seu dia a dia, e também relacioná-las às unidades padronizadas de medidas. Oriente para que resolvam a atividade individualmente, e em seguida, troque ideia com seus colegas, a fim de verificarem se as estratégias utilizadas e os resultados são iguais.
Propósito: Avaliar se os objetivos propostos nesta aula foram alcançados.
Materiais complementares:
Resolução da atividade complementar
Sugestão de adaptação para ensino remoto
Código do plano MAT5_20GRM05
Recursos
- Necessários: -
- Opcionais: calculadora
Para este plano, foque na etapa Retomada e Discussão das soluções
Retomada
Professor(a), você pode realizar a Retomada deste plano com seus alunos, seja em uma aula síncrona ou assíncrona. Compartilhe com a turma os slides presentes nesta atividade. Você não precisa providenciar balanças de diferentes tipos, pode procurar por suas imagens na internet e apresentar suas características aos alunos. Caso considere viável, compartilhe, em formato de texto, os questionamentos presentes no “Discuta com a turma” para fomentar as discussões.
Atividade principal
Professor(a), compartilhe com a turma o slide presente nesta atividade. Como a atividade propõe uma medição do “peso” das mochilas essa etapa não precisa ser realizada. Você pode partir diretamente para a discussão das soluções.
Discussão das soluções
Professor(a), compartilhe com a turma as considerações presentes nesta etapa do plano de aula e utilize os questionamentos presentes no “Discuta com a turma” para fomentar a reflexão. Deixar para os alunos a leitura e interpretação dos slides dessa etapa da aula pode confundi-los. Então, caso a aula esteja ocorrendo de forma síncrona, sugerimos que você verbalize cada etapa da resolução mostrando um slide por vez. Caso a aula esteja ocorrendo de forma assíncrona, você pode gravar um vídeo mostrando a solução e refletindo sobre os procedimentos realizados.
Encerramento
Professor(a), solicite que os alunos registrem em seus cadernos a conclusão que chegam sobre a relação massa, quilogramas e gramas. Caso considere viável, compartilhe com os estudantes o slide presente nesta etapa do plano de aula.
Raio X
O problema proposto no Raio X pode ser enviado para os alunos e solicitado como uma “tarefa” a ser entregue em momento a ser combinado com a turma.
Convite às famílias
Professor(a), sugira que os alunos socializem com seus familiares o que aprenderam nesta aula sobre o “peso” recomendado para as mochilas escolares. Você pode sugerir que eles leiam juntos o artigo a seguir: https://gnt.globo.com/maes-e-filhos/noticia/qual-e-o-peso-ideal-da-mochila-escolar-quiroprata-responde-a-duvidas.ghtml. E também pode sugerir que eles calculem para cada integrante da família o “peso” máximo que podem carregar em suas mochilas.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Rosélia Sezerino Fenner
Mentor: Fabio Menezes da Silva
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF05 MA19) Resolver e elaborar problemas envolvendo medidas das grandezas comprimento, área, massa, tempo, temperatura e capacidade, recorrendo a transformações entre as unidades mais usuais em contextos socioculturais.
Objetivos específicos
Estimar, identificar e relacionar unidades padronizadas de medidas de massa, envolvendo situações-problemas.
Conceito-chave
Medidas de massa
Recursos necessários
- Balança para pesagem dos alunos (pode ser do tipo mecânica antropométrica).
- Se possível, diversos modelos de balanças (de precisão, de dois pratos, de precisão de bolso, eletrônica neonatal, balança digital, entre outras que conseguir.
- Embalagens de alimentos : 4 embalagens de 250 g (café, margarina... ), 2 com 500 g (fubá, margarina, macarrão ...), 1 embalagem com 1 kg (açúcar, margarina, farinha, etc)
- Lápis, borracha, caderno.
- Dicionário.
- Atividade impressa ou não para colar no caderno.

















