Resumo da Aula
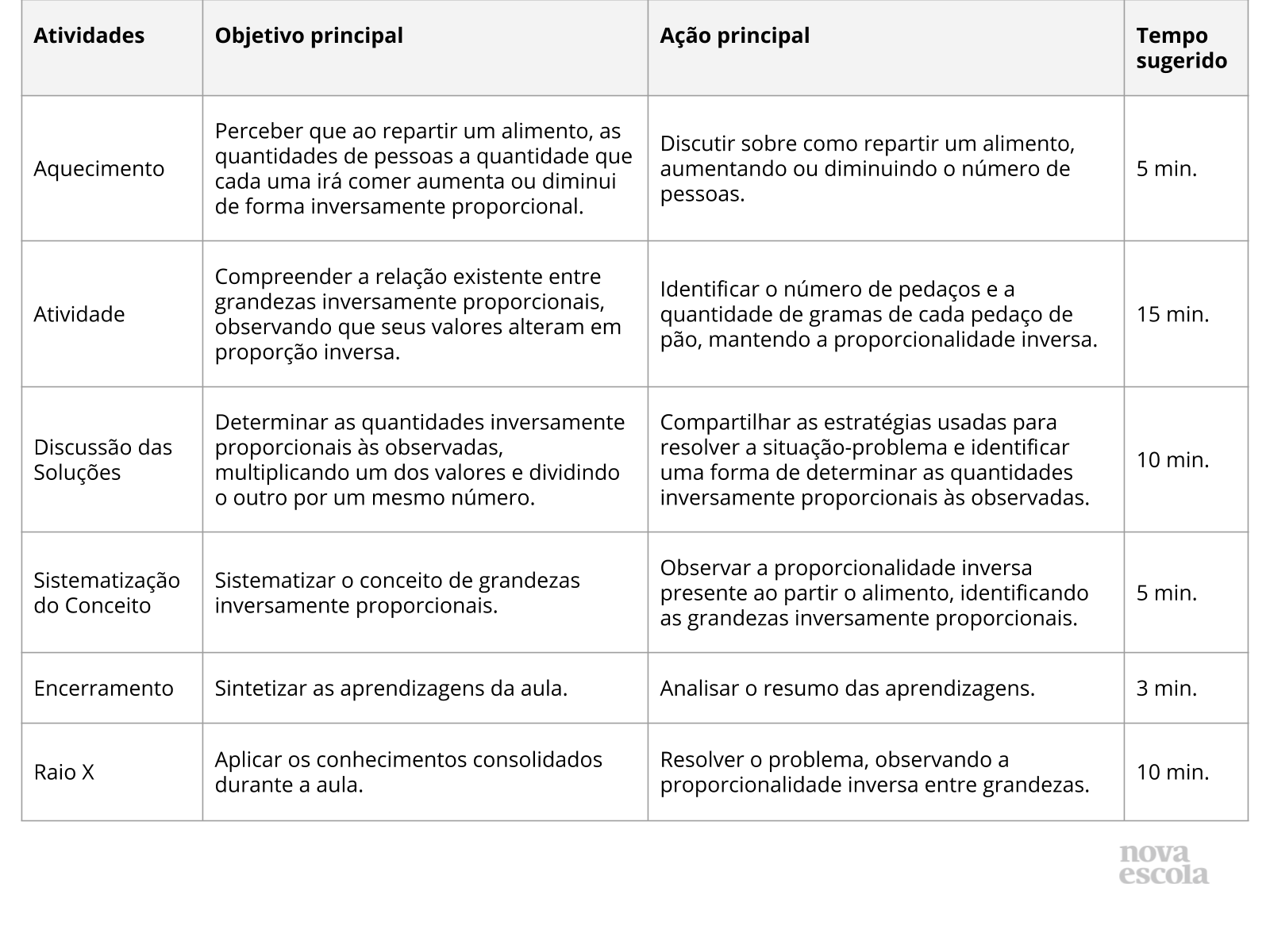
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento

Tempo sugerido: 5 minutos.
Orientações: Inicie a aula perguntando aos alunos sobre o que ocorre com a quantidade de alimento que cada pessoa irá comer se repartirmos esse alimento entre o dobro do número inicial de pessoas. Pergunte também sobre o que ocorre com a quantidade que cada um irá comer se o alimento for repartido entre a metade do número inicial de pessoas. Ouça as respostas e peça que tentem explicar a relação existente entre o número de pessoas e a quantidade de alimento que cada uma irá comer.
Propósito: Possibilitar que os alunos percebam que o número de pessoas e a quantidade de alimento que cada uma irá comer aumenta ou diminui proporcionalmente, de forma inversa.
Discuta com a turma:
- Aumentando o número de pessoas, o que ocorre com a quantidade de alimento que cada uma irá comer? E diminuindo o número de pessoas?
- Há alguma relação entre os números nesse aumento ou diminuição?
Atividade Principal

Tempo sugerido: 15 minutos. (Slides 4 e 5).
Orientações: Peça que, individualmente, os alunos reflitam sobre a atividade e respondam ao questionamento do Slide 5. Em seguida, deixe que discutam com um colega suas soluções e modos de resolver a atividade. Reserve um tempo para um debate coletivo e deixe que as duplas compartilhem o que discutiram.
Propósito: Fazer com que os alunos percebam a relação existente entre grandezas inversamente proporcionais, observando que alterando um dos valores, o outro também altera em proporção inversa.
Discuta com a turma:
- Aumentando a quantidade de gramas de cada pedaço, o que ocorre com o número de pedaços de pão? E se a quantidade de gramas de cada pedaço diminuir?
- Que relação existe entre o número de pedaços e a quantidade de gramas de cada pedaço de pão?
Materiais complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade Principal

Tempo sugerido: 15 minutos. (Slides 4 e 5).
Orientações: Peça que, individualmente, os alunos reflitam sobre a atividade e respondam ao questionamento do Slide 5. Em seguida, deixe que discutam com um colega suas soluções e modos de resolver a atividade. Reserve um tempo para um debate coletivo e deixe que as duplas compartilhem o que discutiram.
Propósito: Fazer com que os alunos percebam a relação existente entre grandezas inversamente proporcionais, observando que alterando um dos valores, o outro também altera em proporção inversa.
Discuta com a turma:
- Aumentando a quantidade de gramas de cada pedaço, o que ocorre com o número de pedaços de pão? E se a quantidade de gramas de cada pedaço diminuir?
- Que relação existe entre o número de pedaços e a quantidade de gramas de cada pedaço de pão?
Discussão das Soluções
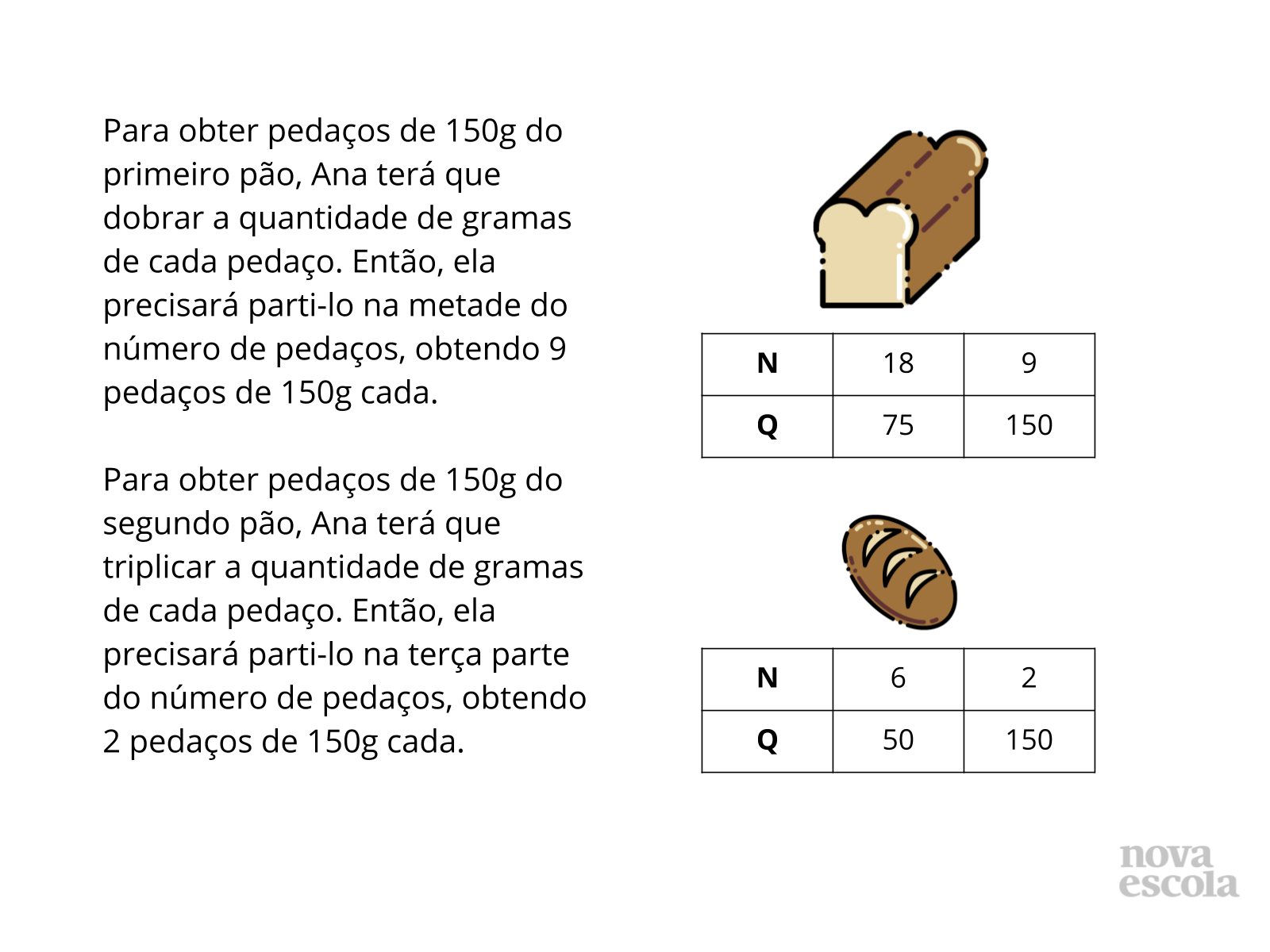
Orientações: Depois que os alunos compartilharem as estratégias deles, peça que observem que diferentes estratégias podem ser utilizadas para resolver o problema. A seguir, passe para esta série de slides, onde os alunos conhecerão uma forma de encontrar os valores proporcionais ao número de pedaços e à quantidade de gramas de cada pedaço de pão apresentados, que se relacionam de forma inversa.
Propósito: Fazer uma síntese das ideias discutidas até o momento.
Discuta com a turma:
- Sabendo a quantidade de gramas de cada pedaço de pão, como podemos identificar a quantidade correspondente de pedaços em que ele pode ser partido?
- Considerando a quantidade de pedaços em que o pão será partido, o que devemos fazer para identificarmos a quantidade de gramas de cada pedaço?
Discussão das Soluções

Orientações: Depois que os alunos compartilharem as estratégias deles, peça que observem que diferentes estratégias podem ser utilizadas para resolver o problema. A seguir, passe para esta série de slides, onde os alunos conhecerão uma forma de encontrar os valores proporcionais ao número de pedaços e à quantidade de gramas de cada pedaço de pão apresentados, que se relacionam de forma inversa.
Propósito: Fazer uma síntese das ideias discutidas até o momento.
Discuta com a turma:
- Sabendo a quantidade de gramas de cada pedaço de pão, como podemos identificar a quantidade correspondente de pedaços em que ele pode ser partido?
- Considerando a quantidade de pedaços em que o pão será partido, o que devemos fazer para identificarmos a quantidade de gramas de cada pedaço?
Discussão das Soluções
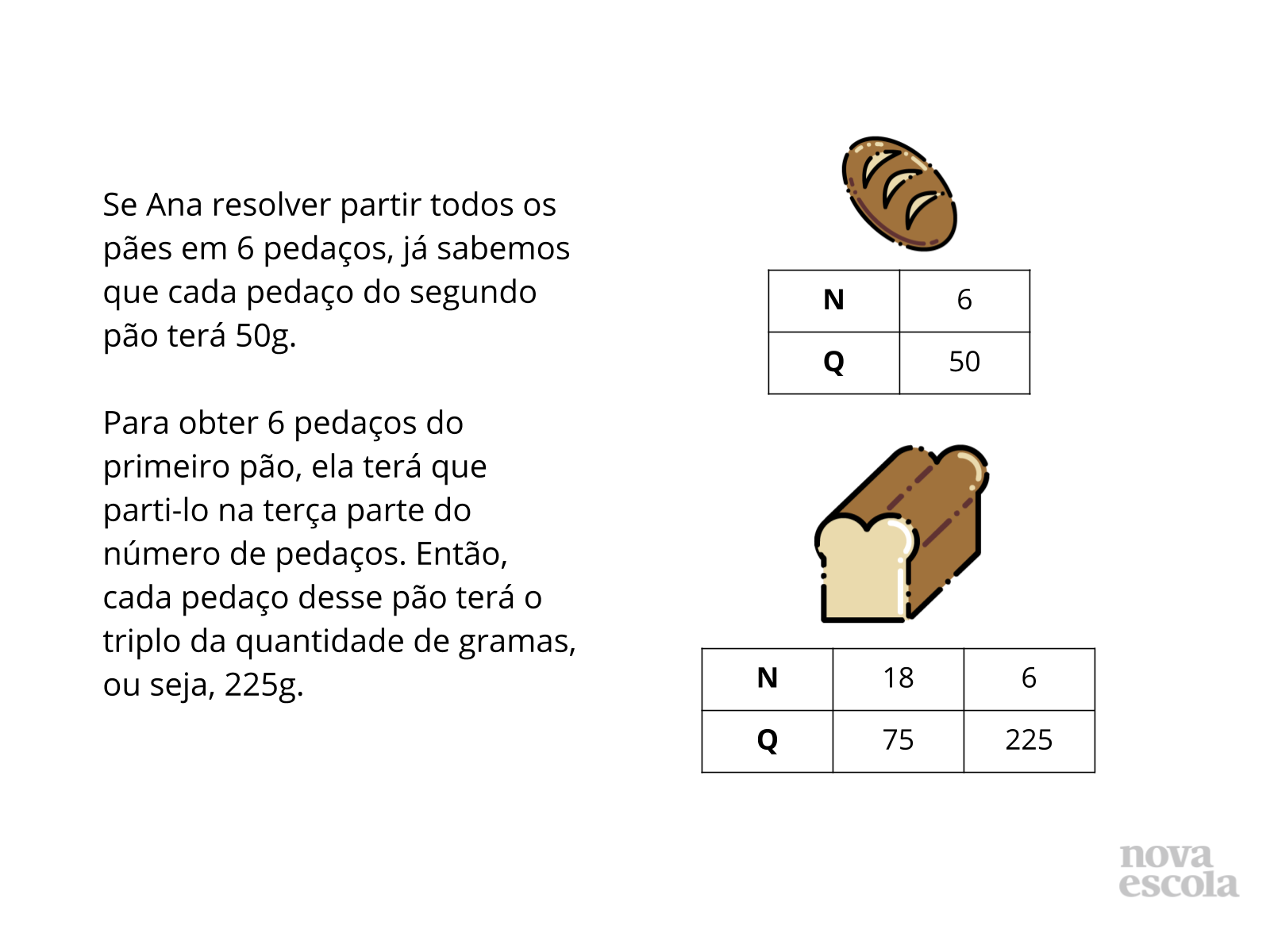
Orientações: Depois que os alunos compartilharem as estratégias deles, peça que observem que diferentes estratégias podem ser utilizadas para resolver o problema. A seguir, passe para esta série de slides, onde os alunos conhecerão uma forma de encontrar os valores proporcionais ao número de pedaços e à quantidade de gramas de cada pedaço de pão apresentados, que se relacionam de forma inversa.
Propósito: Fazer uma síntese das ideias discutidas até o momento.
Discuta com a turma:
- Sabendo a quantidade de gramas de cada pedaço de pão, como podemos identificar a quantidade correspondente de pedaços em que ele pode ser partido?
- Considerando a quantidade de pedaços em que o pão será partido, o que devemos fazer para identificarmos a quantidade de gramas de cada pedaço?
Discussão das Soluções

Orientações: Depois que os alunos compartilharem as estratégias deles, peça que observem que diferentes estratégias podem ser utilizadas para resolver o problema. A seguir, passe para esta série de slides, onde os alunos conhecerão uma forma de encontrar os valores proporcionais ao número de pedaços e à quantidade de gramas de cada pedaço de pão apresentados, que se relacionam de forma inversa.
Propósito: Fazer uma síntese das ideias discutidas até o momento.
Discuta com a turma:
- Sabendo a quantidade de gramas de cada pedaço de pão, como podemos identificar a quantidade correspondente de pedaços em que ele pode ser partido?
- Considerando a quantidade de pedaços em que o pão será partido, o que devemos fazer para identificarmos a quantidade de gramas de cada pedaço?
Sistematização do Conceito

Tempo sugerido: 5 minutos.
Orientações: Encerre a atividade retomando com os alunos a proporcionalidade inversa existente entre o número de pedaços e a quantidade de gramas de cada pedaço de pão. Sistematize o conceito de grandezas inversamente proporcionais.
Propósito: Sistematizar o conceito de grandezas inversamente proporcionais.
Encerramento

Tempo sugerido: 3 minutos.
Orientações: Destaque com os alunos a proporcionalidade inversa existente entre o número de pedaços e o tamanho de cada pedaço de um alimento. Reforce que essas grandezas são inversamente proporcionais.
Propósito: Sintetizar as aprendizagens da aula.
Raio X

Tempo sugerido: 10 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem. Circule pela sala para verificar como os alunos estão resolvendo. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando as soluções no quadro.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito da proporcionalidade inversa.
Discuta com a turma:
- Aumentando o número de pessoas, o que ocorre com a quantidade de bolo? E se o número de pessoas diminuir?
- Há alguma relação entre os números nesse aumento ou diminuição?
Materiais complementares:
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.