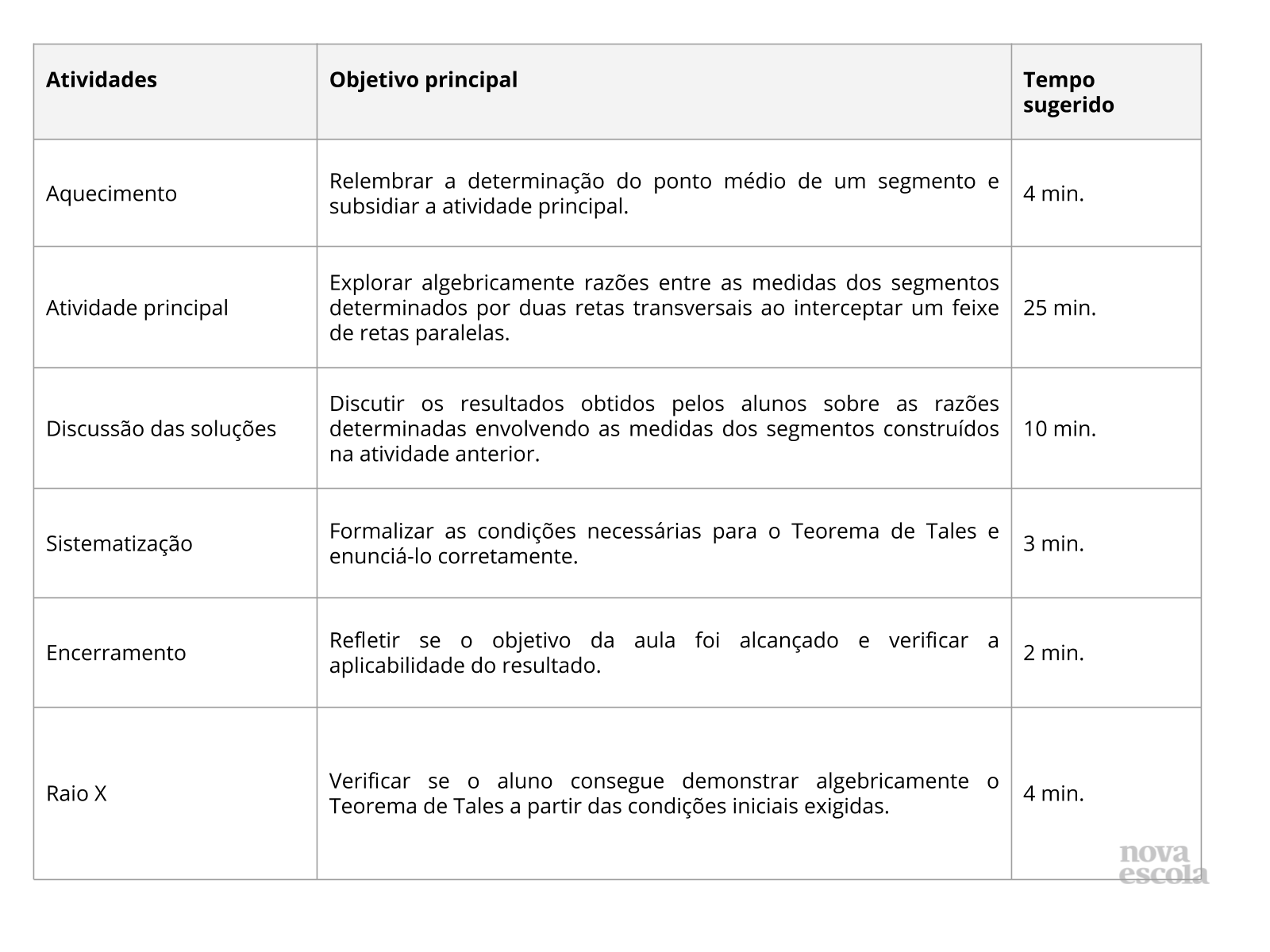
Resolução das atividades
Plano de Aula
Plano de aula: Traçando (várias) paralelas
Plano 6 de uma sequência de 6 planos. Veja todos os planos sobre Explorando ângulos, retas e suas relações
Descrição
(EF09MA10) Demonstrar relações simples entre os ângulos formados por retas paralelas cortadas por uma transversal.
Objetivos específicos
- Determinar o ponto médio de um segmento com auxílio de régua e compasso;
- Representar algebricamente a razão entre dois segmentos;
- Demonstrar algebricamente o Teorema de Tales num feixe de retas paralelas cortado por duas transversais.
Habilidades BNCC:
Objetivos de aprendizagem
- Determinar o ponto médio de um segmento com auxílio de régua e compasso;
- Representar algebricamente a razão entre dois segmentos;
- Demonstrar algebricamente o Teorema de Tales num feixe de retas paralelas cortado por duas transversais.
Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão. O tempo sugerido prevê 48 minutos de atividade e 2 minutos para compartilhar com a turma o objetivo da aula.
Objetivo

Tempo sugerido: 2 minutos
Orientações: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento
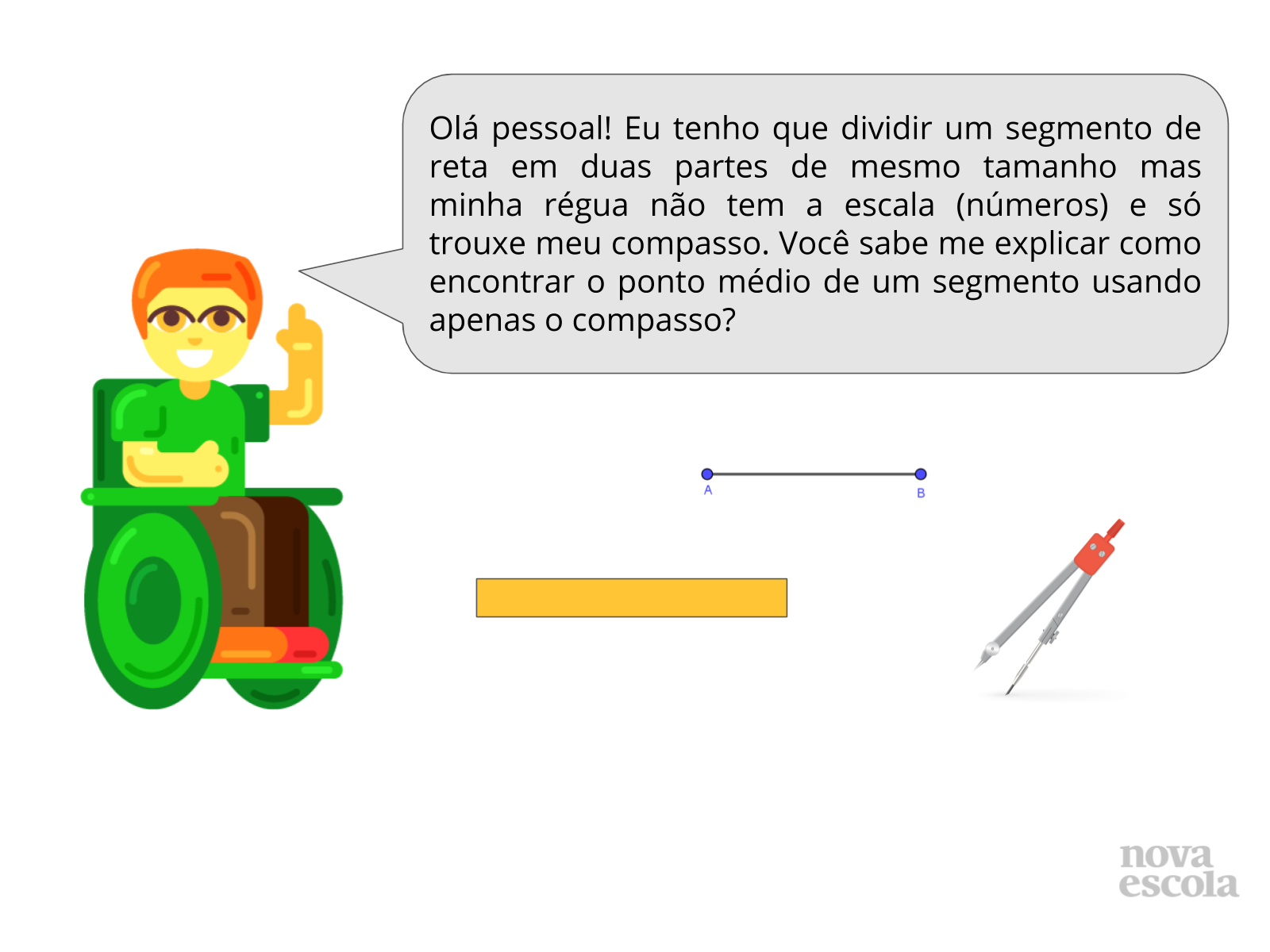
Tempo sugerido: 4 minutos (slides 3 e 4)
Orientações:
Inicie a aula projetando a pergunta ou lendo para a turma o questionamento. Dê alguns minutos para que os alunos pensem em como deverão posicionar o compasso sobre o segmento e quais condições deverá ter o raio para que a intersecção entre os arcos determine a mediana do segmento. Depois de algumas experimentações os alunos deverão concluir que devem posicionar a ponta seca do compasso nas extremidades e utilizar o raio igual ou maior que a metade do segmento para traçar os arcos e determinar a mediana do segmento.
Em seguida pergunte aos alunos como eles poderiam representar a razão entre os segmentos determinados pelo ponto médio encontrado. Questione os alunos sobre como representar as medidas desconhecidas, se eles devem utilizar a mesma incógnita para ambos segmentos e porquê.
Propósito:
Relembrar a determinação do ponto médio de um segmento e subsidiar a Atividade Principal.
Discuta com a turma:
- Onde devemos colocar a ponta seca do compasso inicialmente?
- Qual deverá ser a abertura do compasso (raio) para determinarmos os arcos?
- O quê garante que o ponto determinado é realmente o ponto médio do segmento?
Materiais complementares:
Atividade Aquecimento:
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/seU5G3PrNBNbF6AQSFuDESvwach63UeJab2NDdArZktuFDAc5zWeMeSnk4q5/resolucao-das-atividades-mat9-10geo06.pdf
Aquecimento
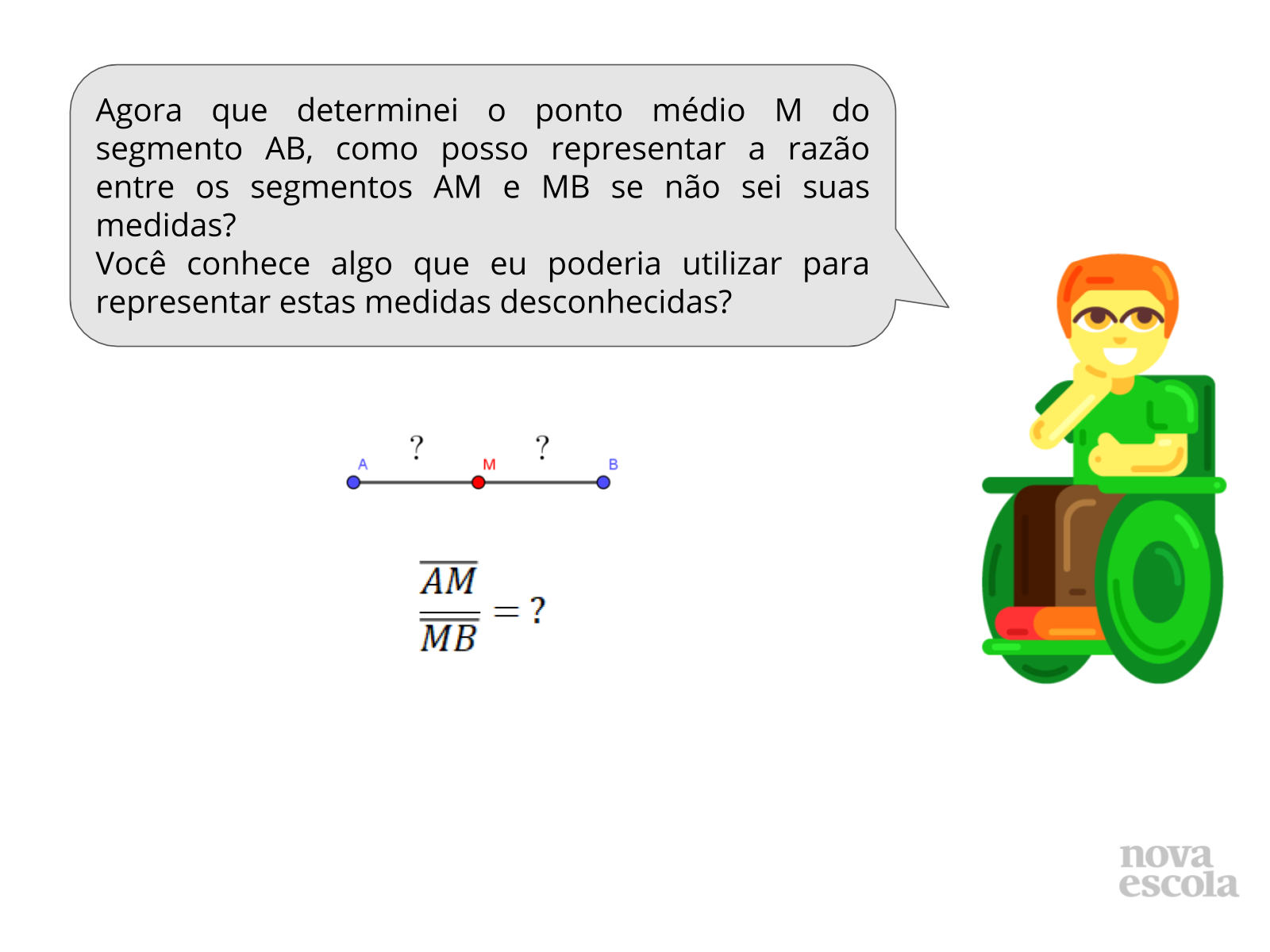
Tempo sugerido: 4 minutos (slides 3 e 4)
Orientações:
Inicie a aula projetando a pergunta ou lendo para a turma o questionamento. Dê alguns minutos para que os alunos pensem em como deverão posicionar o compasso sobre o segmento e quais condições deverá ter o raio para que a intersecção entre os arcos determine a mediana do segmento. Depois de algumas experimentações os alunos deverão concluir que devem posicionar a ponta seca do compasso nas extremidades e utilizar o raio igual ou maior que a metade do segmento para traçar os arcos e determinar a mediana do segmento.
Em seguida pergunte aos alunos como eles poderiam representar a razão entre os segmentos determinados pelo ponto médio encontrado. Questione os alunos sobre como representar as medidas desconhecidas, se eles devem utilizar a mesma incógnita para ambos segmentos e porquê.
Propósito:
Relembrar a determinação do ponto médio de um segmento e subsidiar a Atividade Principal.
Discuta com a turma:
- Onde devemos colocar a ponta seca do compasso inicialmente?
- Qual deverá ser a abertura do compasso (raio) para determinarmos os arcos?
- O quê garante que o ponto determinado é realmente o ponto médio do segmento?
Materiais complementares:
Atividade Aquecimento: https://nova-escola-producao.s3.amazonaws.com/nrm8brRfSMC2CEbRgz5wnxbXtxSwMm7S2GjamGeFTe9t7D2vfb3xuXWMyBda/atividade-aquecimento-mat9-10geo06.pdf
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/seU5G3PrNBNbF6AQSFuDESvwach63UeJab2NDdArZktuFDAc5zWeMeSnk4q5/resolucao-das-atividades-mat9-10geo06.pdf
Atividade principal
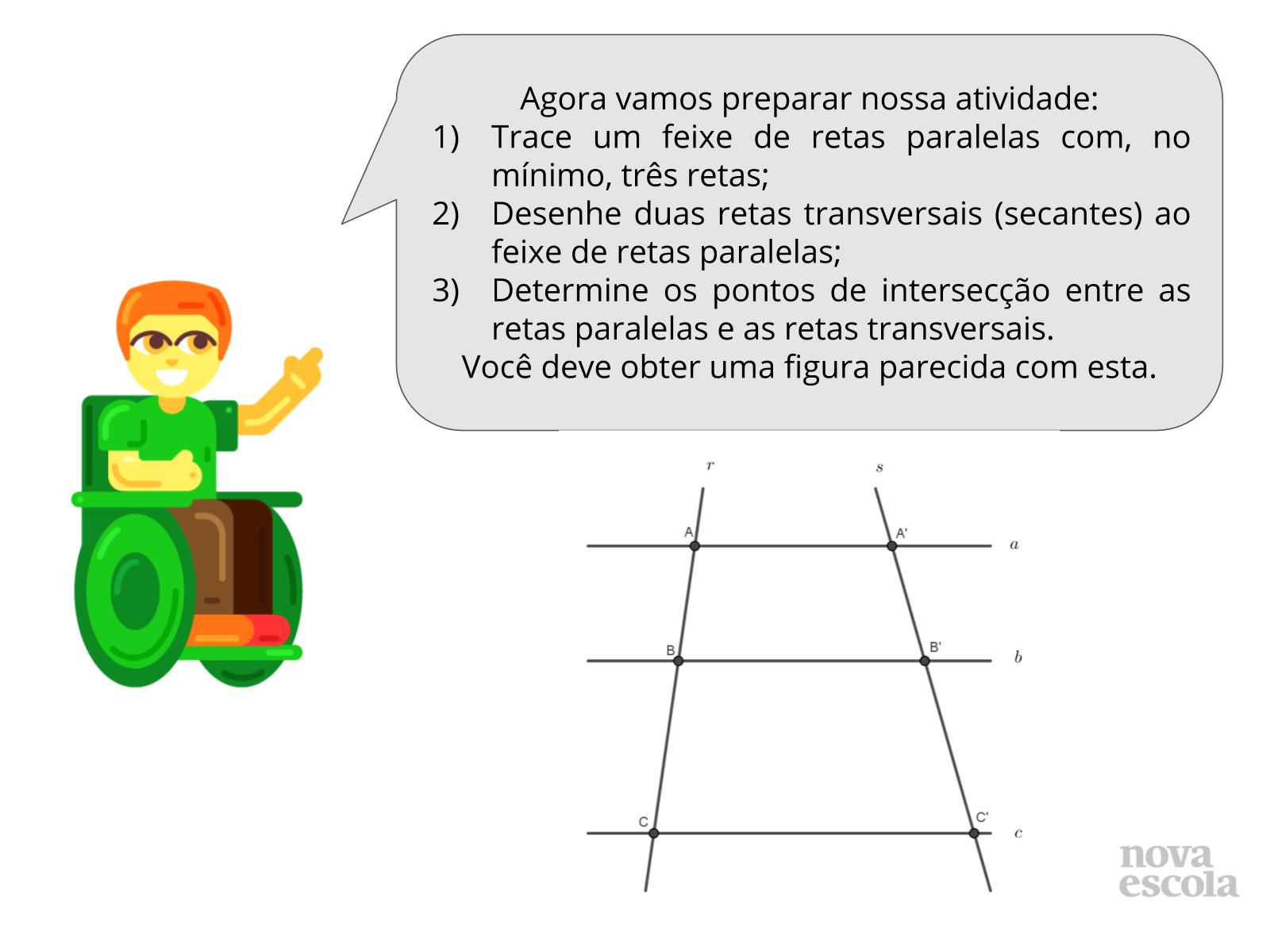
Tempo sugerido: 25 minutos (slides 5 e 6)
Orientações:
Organize a turma em duplas produtivas, distribua algumas folhas de sulfite e verifique se todos possuem régua e compasso disponíveis.
Na primeira etapa da atividade leia as orientações do slide 4 e peça para que cada dupla produza a figura desejada (feixe de retas paralelas interceptado por duas retas transversais). Enquanto os alunos realizam esta etapa percorra as carteiras e verifique se os traçados estão corretos, se os alunos utilizam a notação adequada (letras minúsculas para retas, maiúsculas para os pontos).
Quando todos os alunos tiverem desejado a figura desejada peça para que leiam silenciosamente as orientações do slide 5 e pergunte se há alguma dúvida referente a alguma das orientações. Explique as dúvidas que por acaso surgirem e, se necessário, realize um exemplo para que os alunos façam suas explorações.
Propósito:
Na primeira etapa produzir a figura inicial que será utilizada na elaboração das hipóteses.
Na segunda etapa realizar uma exploração algébrica envolvendo razões entre as medidas dos segmentos determinados por duas retas transversais ao interceptar um feixe de retas paralelas.
Discuta com a turma:
- Qual a principal característica de um feixe de retas paralelas? E de retas transversais?
- Todos os segmentos determinados apresentam a mesma medida? Como deve ser as incógnitas para representar as medidas dos segmentos?
- Qual a principal característica de um ponto médio de um segmento? Como deve ser a incógnita a ser utilizada sabendo desta característica?
- Como podemos elaborar uma razão envolvendo as medidas dos segmentos determinados pela primeira transversal? E pela segunda transversal?
- Comparando as razões em cada transversal você percebe algo? O quê podemos afirmar em relação às razões obtidas?
Materiais complementares:
Atividade Principal: https://nova-escola-producao.s3.amazonaws.com/Jquuw62RjH8w9E2JxNtSJeAmCMbehetJHSECnVwPm6bJFXdxMqB8rhTwkcmh/atividade-principal-mat9-10geo06.pdf
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/seU5G3PrNBNbF6AQSFuDESvwach63UeJab2NDdArZktuFDAc5zWeMeSnk4q5/resolucao-das-atividades-mat9-10geo06.pdf
Atividade principal

Tempo sugerido: 25 minutos (slides 5 e 6)
Orientações:
Organize a turma em duplas produtivas, distribua algumas folhas de sulfite e verifique se todos possuem régua e compasso disponíveis.
Na primeira etapa da atividade leia as orientações do slide 4 e peça para que cada dupla produza a figura desejada (feixe de retas paralelas interceptado por duas retas transversais). Enquanto os alunos realizam esta etapa percorra as carteiras e verifique se os traçados estão corretos, se os alunos utilizam a notação adequada (letras minúsculas para retas, maiúsculas para os pontos).
Quando todos os alunos tiverem desejado a figura desejada peça para que leiam silenciosamente as orientações do slide 5 e pergunte se há alguma dúvida referente a alguma das orientações. Explique as dúvidas que por acaso surgirem e, se necessário, realize um exemplo para que os alunos façam suas explorações.
Propósito:
Na primeira etapa produzir a figura inicial que será utilizada na elaboração das hipóteses.
Na segunda etapa realizar uma exploração algébrica envolvendo razões entre as medidas dos segmentos determinados por duas retas transversais ao interceptar um feixe de retas paralelas.
Discuta com a turma:
- Qual a principal característica de um feixe de retas paralelas? E de retas transversais?
- Todos os segmentos determinados apresentam a mesma medida? Como deve ser as incógnitas para representar as medidas dos segmentos?
- Qual a principal característica de um ponto médio de um segmento? Como deve ser a incógnita a ser utilizada sabendo desta característica?
- Como podemos elaborar uma razão envolvendo as medidas dos segmentos determinados pela primeira transversal? E pela segunda transversal?
- Comparando as razões em cada transversal você percebe algo? O quê podemos afirmar em relação às razões obtidas?
Materiais complementares:
Atividade Principal: https://nova-escola-producao.s3.amazonaws.com/Jquuw62RjH8w9E2JxNtSJeAmCMbehetJHSECnVwPm6bJFXdxMqB8rhTwkcmh/atividade-principal-mat9-10geo06.pdf
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/seU5G3PrNBNbF6AQSFuDESvwach63UeJab2NDdArZktuFDAc5zWeMeSnk4q5/resolucao-das-atividades-mat9-10geo06.pdf
Discussão das soluções
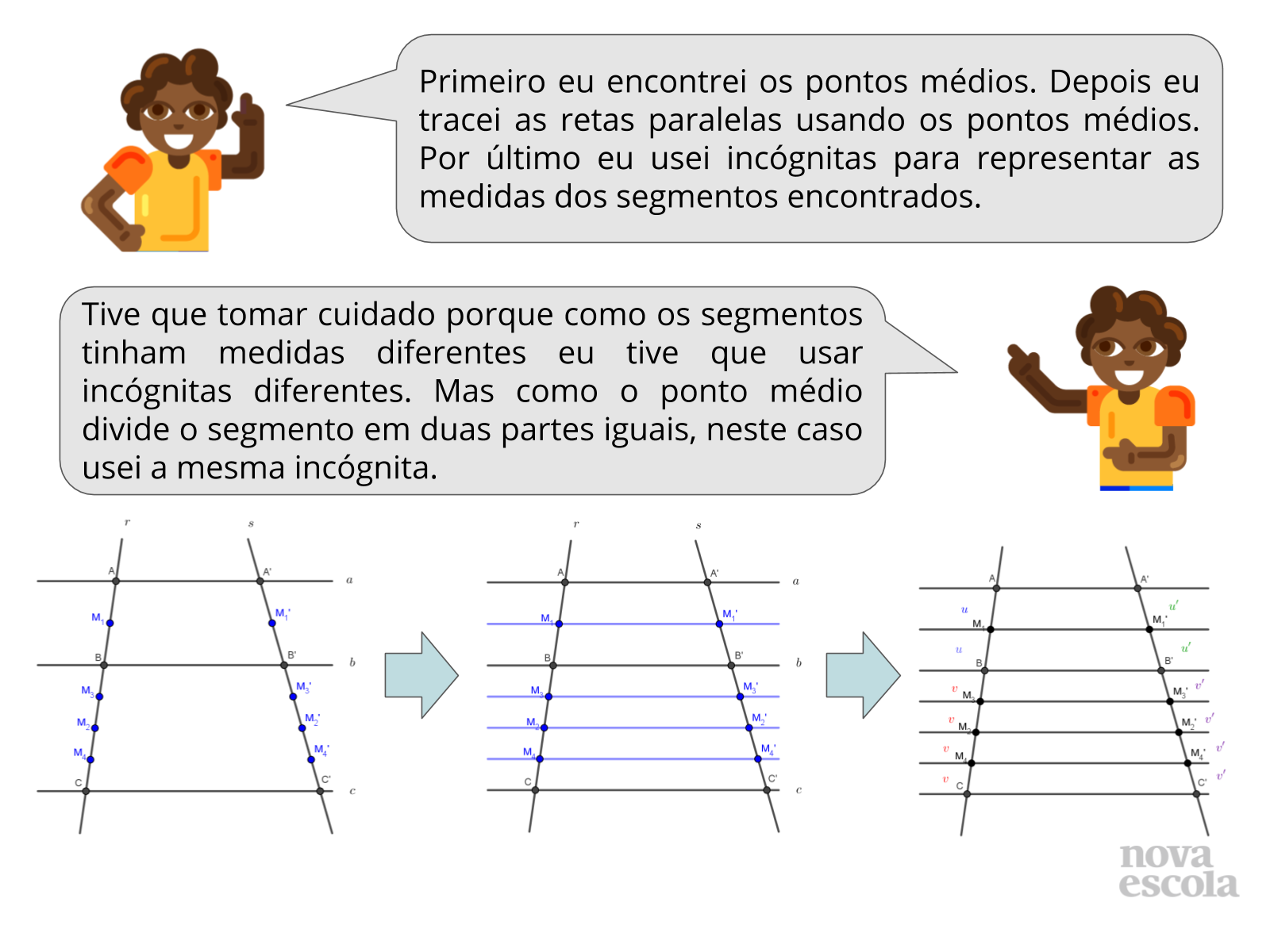
Tempo sugerido: 10 minutos (slides 7 e 8)
Orientações:
Escolha algumas produções elaboradas pelos alunos e peça para que um dos integrantes da dupla explique como foram as etapas usadas em suas construções. Vá perguntando aos alunos quantos pontos médios determinaram em cada transversal, quantas retas paralelas conseguiram traçar e como utilizaram as incógnitas para representar as medidas dos segmentos.
Em seguida peça para o outro membro da dupla contar como elaboraram as razões em cada reta transversal. Questione quais foram os resultados obtidos em cada reta transversal e como ocorreu a comparação entre as razões obtidas.
Faça isto com pelo menos duas duplas diferentes para que a turma verifique que independente da quantidade de retas traçadas, haverá sempre a proporcionalidade direta envolvida na situação.
Propósito:
Comunicar e discutir os resultados obtidos na exploração anterior envolvendo os segmentos determinados pelas transversais no feixe de paralelas.
Discuta com a turma:
- Quantos pontos médios você determinou na primeira reta transversal? E na segunda reta transversal?
- Quantas retas paralelas você conseguiu determinar? E quantos segmentos de retas foram determinados em cada transversal?
- Você utilizou a mesma incógnita ou incógnitas diferentes para representar as medidas dos segmentos? Por quê?
- Qual foi a razão que você elaborou a partir das medidas da primeira reta transversal? E qual foi a razão obtida na segunda transversal?
- O quê você percebeu ao comparar as razões obtidas?
Materiais complementares:
Guia de intervenções: https://nova-escola-producao.s3.amazonaws.com/Mx4sZWwRgXg2VJWG6FW4dk89purvk8rSdGmPH3ax6b5YVGWmE4p6bS59nkzD/guia-de-intervencoes-mat9-10geo06.pdf
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/seU5G3PrNBNbF6AQSFuDESvwach63UeJab2NDdArZktuFDAc5zWeMeSnk4q5/resolucao-das-atividades-mat9-10geo06.pdf
Discussão das soluções
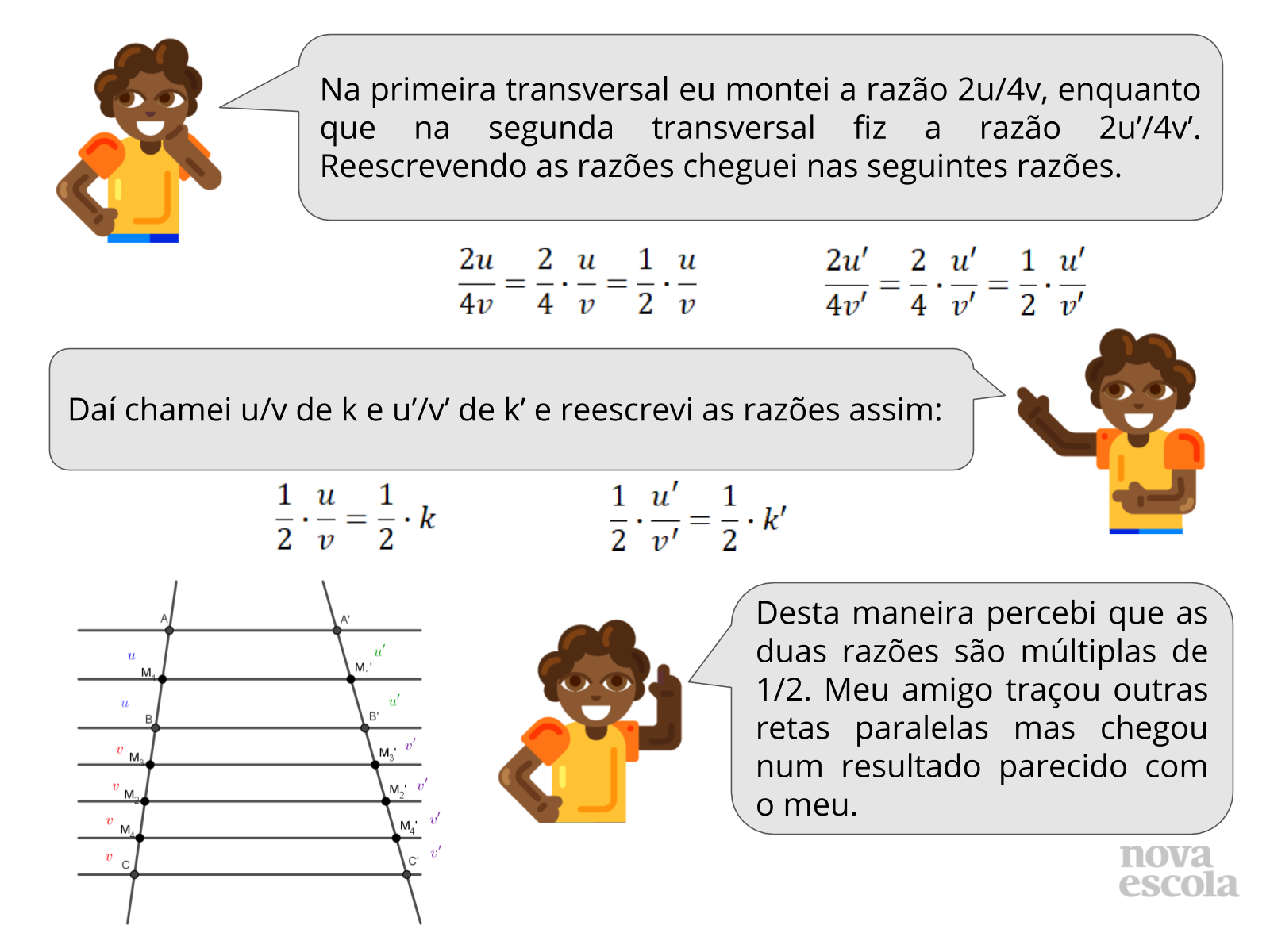
Tempo sugerido: 10 minutos (slides 7 e 8)
Orientações:
Escolha algumas produções elaboradas pelos alunos e peça para que um dos integrantes da dupla explique como foram as etapas usadas em suas construções. Vá perguntando aos alunos quantos pontos médios determinaram em cada transversal, quantas retas paralelas conseguiram traçar e como utilizaram as incógnitas para representar as medidas dos segmentos.
Em seguida peça para o outro membro da dupla contar como elaboraram as razões em cada reta transversal. Questione quais foram os resultados obtidos em cada reta transversal e como ocorreu a comparação entre as razões obtidas.
Faça isto com pelo menos duas duplas diferentes para que a turma verifique que independente da quantidade de retas traçadas, haverá sempre a proporcionalidade direta envolvida na situação.
Propósito:
Comunicar e discutir os resultados obtidos na exploração anterior envolvendo os segmentos determinados pelas transversais no feixe de paralelas.
Discuta com a turma:
- Quantos pontos médios você determinou na primeira reta transversal? E na segunda reta transversal?
- Quantas retas paralelas você conseguiu determinar? E quantos segmentos de retas foram determinados em cada transversal?
- Você utilizou a mesma incógnita ou incógnitas diferentes para representar as medidas dos segmentos? Por quê?
- Qual foi a razão que você elaborou a partir das medidas da primeira reta transversal? E qual foi a razão obtida na segunda transversal?
- O quê você percebeu ao comparar as razões obtidas?
Materiais complementares:
Guia de intervenções: https://nova-escola-producao.s3.amazonaws.com/Mx4sZWwRgXg2VJWG6FW4dk89purvk8rSdGmPH3ax6b5YVGWmE4p6bS59nkzD/guia-de-intervencoes-mat9-10geo06.pdf
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/seU5G3PrNBNbF6AQSFuDESvwach63UeJab2NDdArZktuFDAc5zWeMeSnk4q5/resolucao-das-atividades-mat9-10geo06.pdf
Sistematização
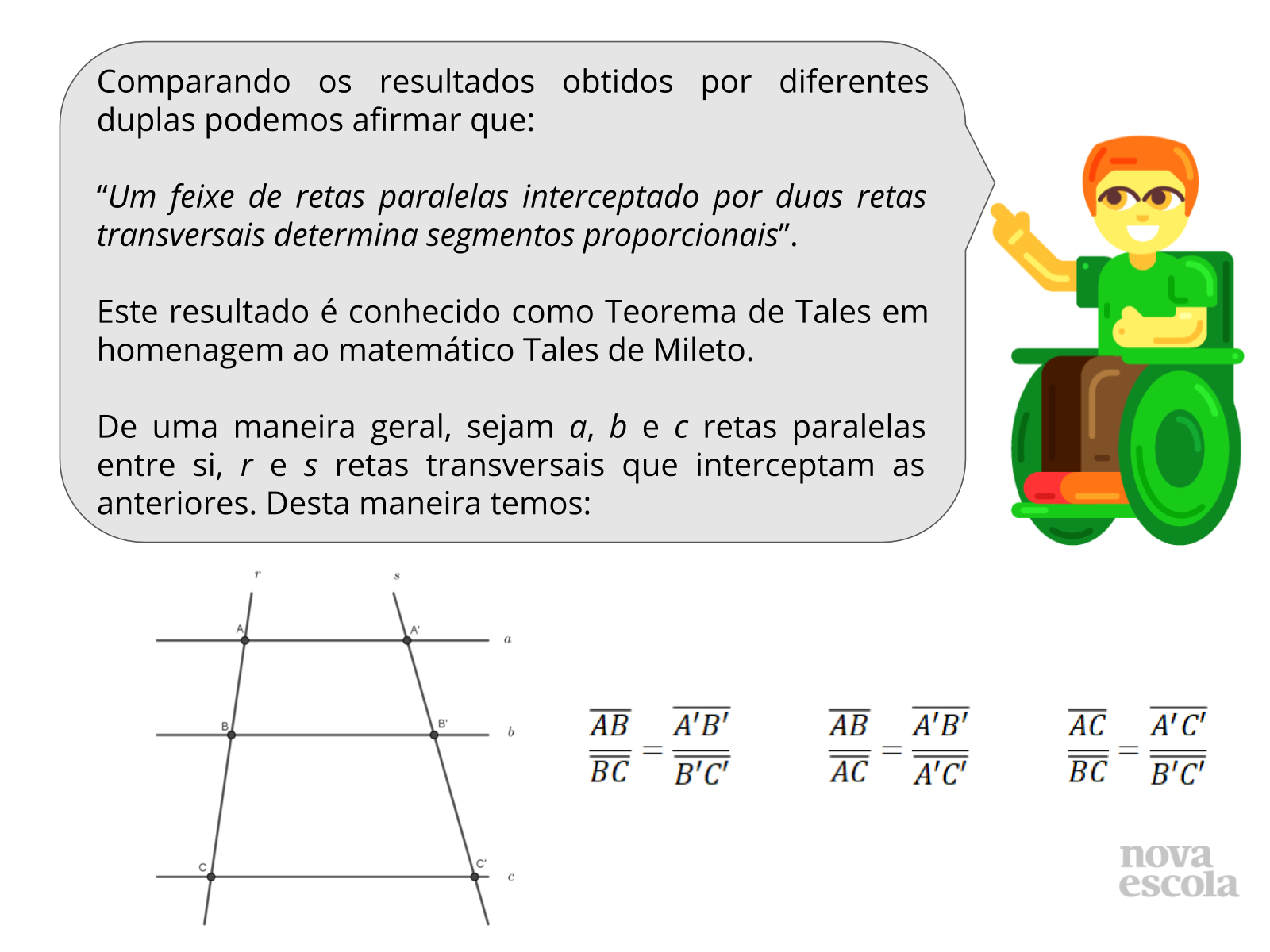
Tempo sugerido: 3 minutos
Orientações:
Retome as etapas desenvolvidas ao longo desta aula junto aos alunos e os auxilie a escrever uma síntese dos resultados obtidos pelas diferentes duplas.
Propósito:
Elaborar uma síntese dos resultados apresentados pelas diferentes duplas constatando o Teorema de Tales.
Discuta com a turma:
- Quais foram as condições iniciais necessárias para chegarmos a conclusão da aula? Qual deve ser a posição das retas inicialmente para que obtermos o resultado final?
- Satisfeitas as condições iniciais da posição das retas qual foi o resultado geral obtido? Ete resultado pode ser aplicado a qualquer figura que apresente as condições iniciais? Por quê?
Encerramento

Tempo sugerido: 2 minutos
Orientações:
Peça para que um aluno faça a leitura das instruções presentes no slide e questione a turma sobre possíveis aplicações do Teorema de Tales.
Propósito:
Refletir sobre o objetivo da aula e verificar quanto é possível utilizar o resultado desenvolvido.
Discuta com a turma:
Sob quais condições podemos utilizar o resultado obtido (Teorema de Tales)?
Raio X
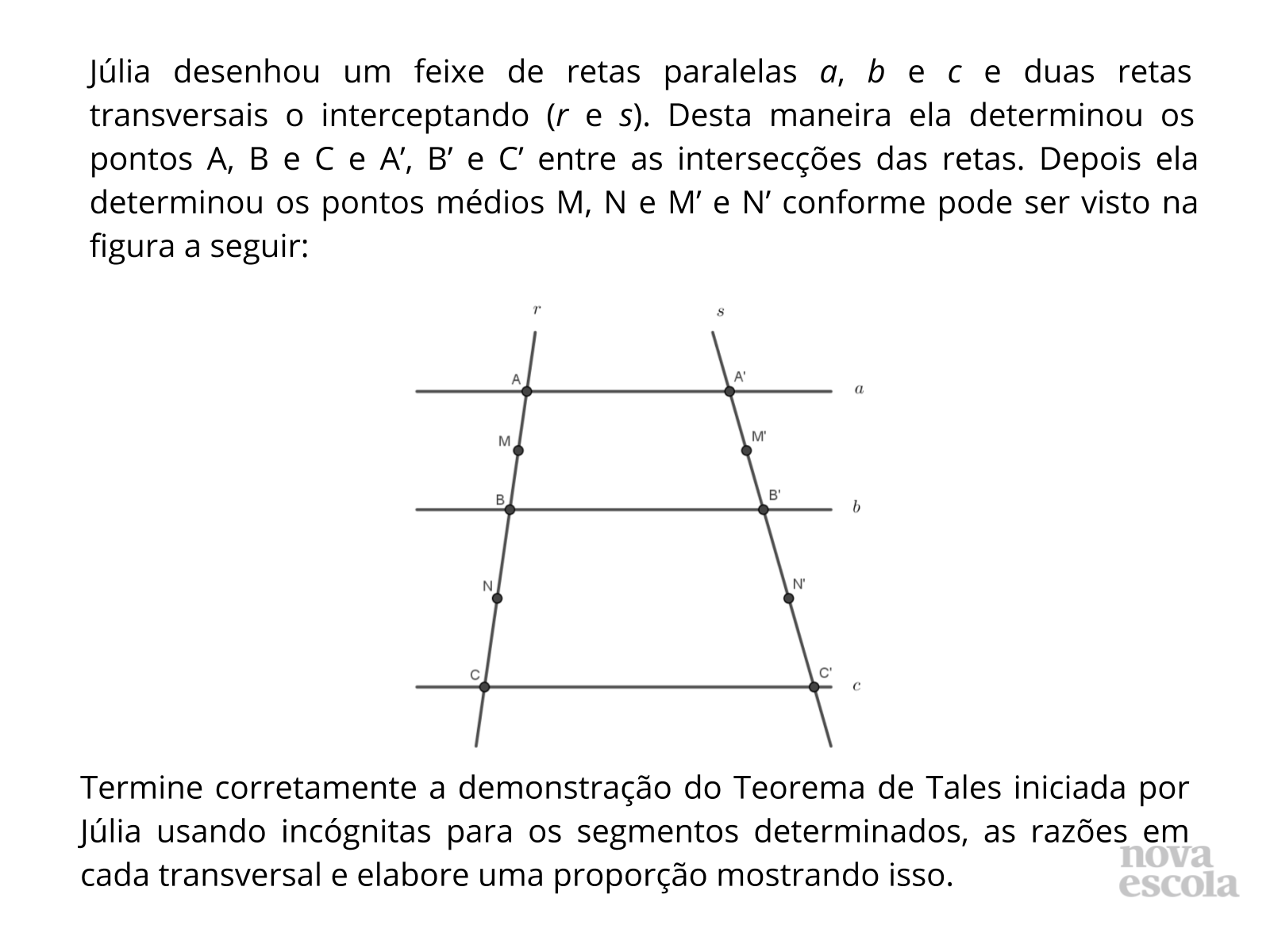
Tempo sugerido: 4 min
Orientações:
Entregue para cada aluno uma cópia da atividade e solicite que leiam atentamente o enunciado. Pergunte se há alguma dúvida em relação ao comando da atividade e a esclareça se houver necessidade. Recolha as respostas e verifique se os alunos desenvolveram adequadamente o objetivo da aula (demonstrar algebricamente o Teorema de Tales).
Propósito:
Verificar se os alunos desenvolveram adequadamente o objetivo da aula.
Discuta com a turma:
- As incógnitas estão adequadas de acordo com os dados da atividade?
- As razões entre as medidas dos segmentos foram elaboradas corretamente em cada reta transversal?
- A proporção determinada demonstra a proporcionalidade existente na figura?
Materiais complementares:
Atividade Raio X: https://nova-escola-producao.s3.amazonaws.com/tXvdW6BjAfAsPbKBZusajKkqGhyvn8qvNZJHpTU74tRrJGnGsMN2qkgAaMaz/atividade-raio-x-mat9-10geo06.pdf
Atividades complementares: https://nova-escola-producao.s3.amazonaws.com/saTQv4Mjx2R5Qbhqnr9yPNYYEakC7gjZ5snSEEh7GhjQfhMABbBnhpeb2edS/atividades-complementares-mat9-10geo06.pdf
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/seU5G3PrNBNbF6AQSFuDESvwach63UeJab2NDdArZktuFDAc5zWeMeSnk4q5/resolucao-das-atividades-mat9-10geo06.pdf
Para o professor
Para o aluno
Sugestão de adaptação para ensino remoto
Código do plano (MAT9_10GEO06)
Ferramentas sugeridas
- Essenciais: Alguma rede social (Whatsapp, Facebook, etc), régua, transferidor, tesoura e papel para anotações.
- Optativas: Smartfone.
Atividade principal
- Determine que, pesquisem sobre as demonstrações do teorema de Tales sobre retas paralelas cortadas por transversais e produzam um parágrafo sobre o que entenderam dela.
Discussão das soluções, sistematização e encerramento
- Na discussão das soluções, diga que decorar as demonstrações não é tão importante, mas elas ajudam a sustentar a matemática como ciência e as suas verdades. Afinal, por que funciona, não é mesmo?
Convite às famílias
Peça para que seus alunos envolvam seus familiares, próximos neste momento, e incentive-os a tentar explicar o que aprenderam a eles.
(EF09MA10) Demonstrar relações simples entre os ângulos formados por retas paralelas cortadas por uma transversal.
Objetivos específicos
- Determinar o ponto médio de um segmento com auxílio de régua e compasso;
- Representar algebricamente a razão entre dois segmentos;
- Demonstrar algebricamente o Teorema de Tales num feixe de retas paralelas cortado por duas transversais.













