Atividade principal
Plano de Aula
Plano de aula: Explorando medidas de capacidade e suas equivalências
Plano 4 de uma sequência de 10 planos. Veja todos os planos sobre Grandezas e Medidas
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Rosélia Sezerino Fenner
Mentor: Fábio Menezes da Silva
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF05MA19) Resolver e elaborar problemas envolvendo medidas das grandezas; comprimento, área massa, tempo, temperatura e capacidade, recorrendo transformações entre as unidades mais usuais em contextos socioculturais.
Objetivos específicos
Explorar situações comuns do dia a dia envolvendo estimativas de medidas capacidade e suas equivalências.
Conceito-chave
Medidas de capacidade.
Recursos necessários
- Tiras de papel (várias), pode ser de folha A4 ou papel craft;
- Atividades impressas em folhas, coladas no caderno ou não;
- Material reciclável : garrafas de 1 L , 2 L, xícaras de aproximadamente 240 mL, colher (sopa), colher (chá), colher (sobremesa), copos descartáveis ou de plástico de diversos tamanhos (200 mL - 250 mL - 100 mL - 150 mL - 50 mL);
- Jarra com capacidades diversas;
- Recipiente com água para experimento;
- Lápis;
- Caderno;
- Borracha.
Habilidades BNCC:
Objetivos de aprendizagem
Explorar situações comuns do dia a dia envolvendo estimativas de medidas capacidade e suas equivalências.
Planeje suas aulas pelo Whatsapp!
Qualidade com economia de tempo
Aula
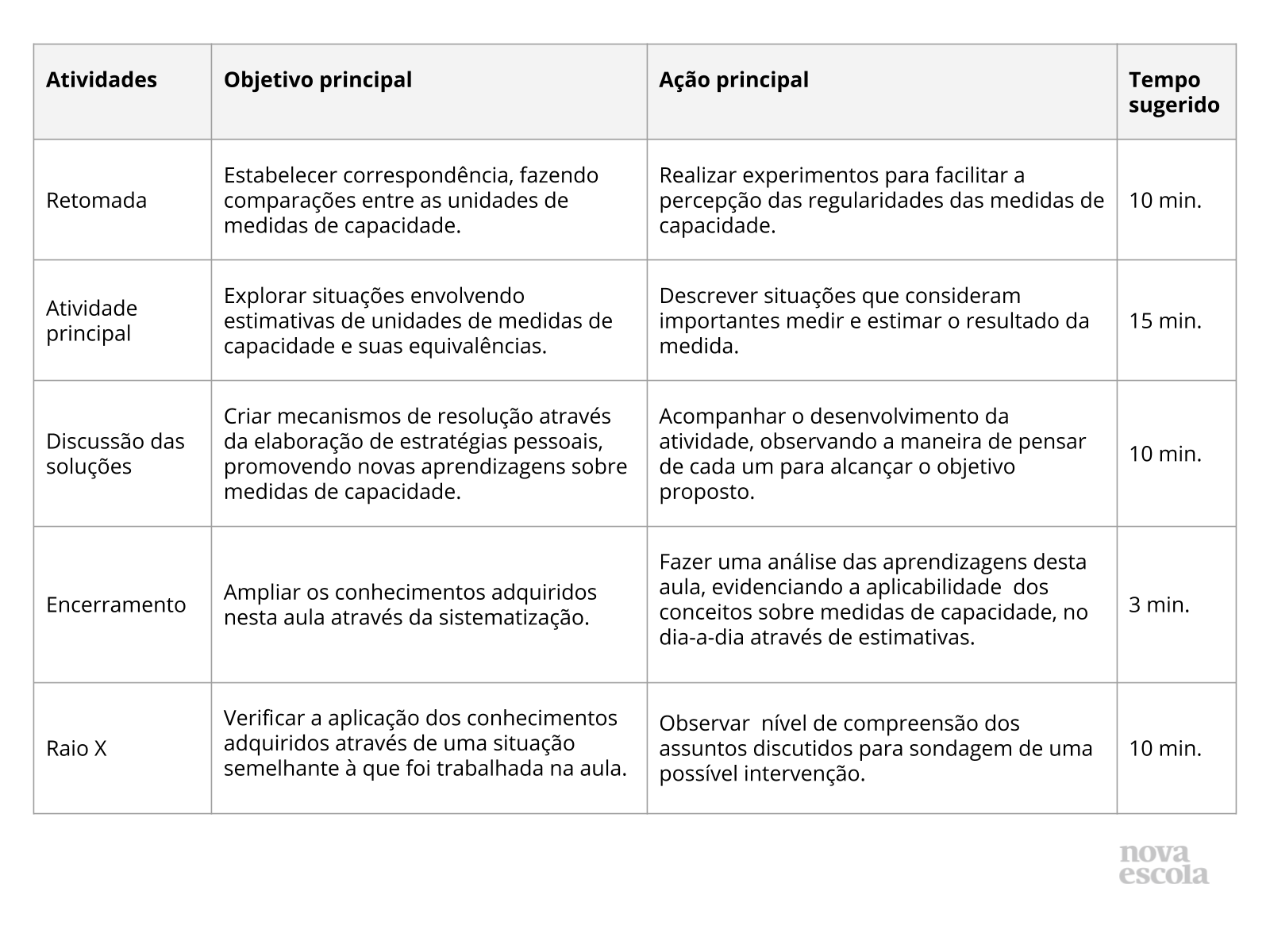
Resumo da aula
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos
Orientação: Leia com os alunos o objetivo da aula. É esse o assunto da aula do dia.
Propósito: Apresentar o objetivo da aula para conhecimento dos alunos.


















