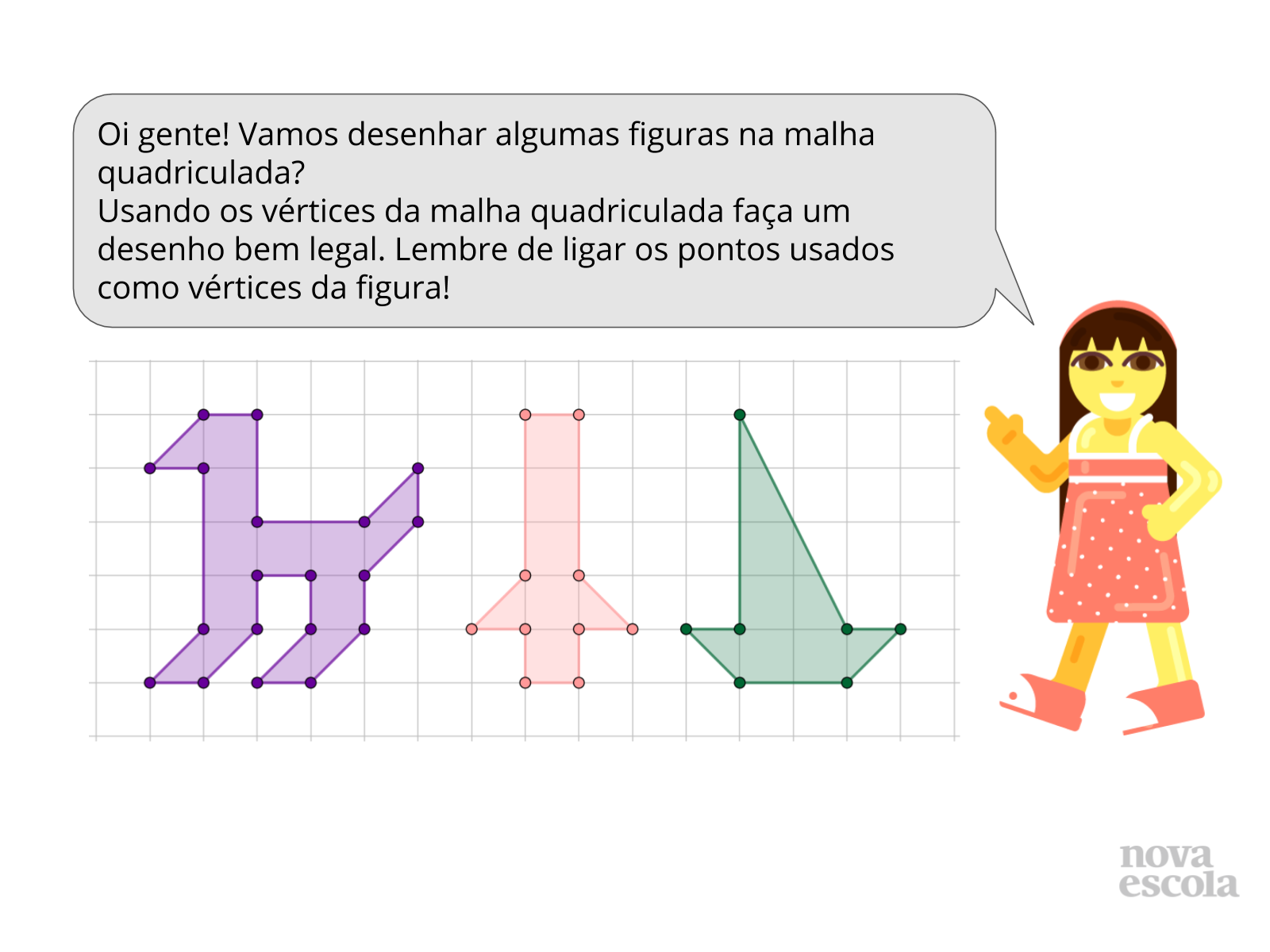
Resumo da aula
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Apresente o objetivo da aula de forma clara, de modo que os alunos percebam o que se deseja alcançar com as atividades a serem desenvolvidas na aula. O professor poderá, caso disponibilize de tempo, utilizar uma caixa de papelão ou usar o ambiente da sala de aula para ilustrar o espaço tridimensional com os alunos.
Propósito: Apresentar o objetivo da aula.
Discuta com a turma:
- Quantas dimensões possui uma caixa ?
Retomada

Tempo sugerido: 6 minutos. (slides 3 e 4) .
Orientações:
Realize a atividade em duplas. Disponibilize a atividade impressa para cada dupla. Caso seja possível, poderá trabalhar a construção de um cubo a partir de sua planificação em uma aula extra ou até mesmo disponibilizar material concreto para que os alunos manipulem.
Propósito: Rever conceitos relacionados aos elementos de um cubo: faces, vértices e arestas.
Discuta com a turma:
- Como se denomina o segmento que une duas faces do cubo?
- Quantas arestas partem de cada vértice?
Materiais complementares para impressão:
Aquecimento
Resolução do aquecimento
Retomada
Tempo sugerido: 6 minutos. (slides 3 e 4) .
Orientações:
Realize a atividade em duplas. Disponibilize a atividade impressa para cada dupla. Caso seja possível, poderá trabalhar a construção de um cubo a partir de sua planificação em uma aula extra ou até mesmo disponibilizar material concreto para que os alunos manipulem.
Propósito: Rever conceitos relacionados aos elementos de um cubo: faces, vértices e arestas.
Discuta com a turma:
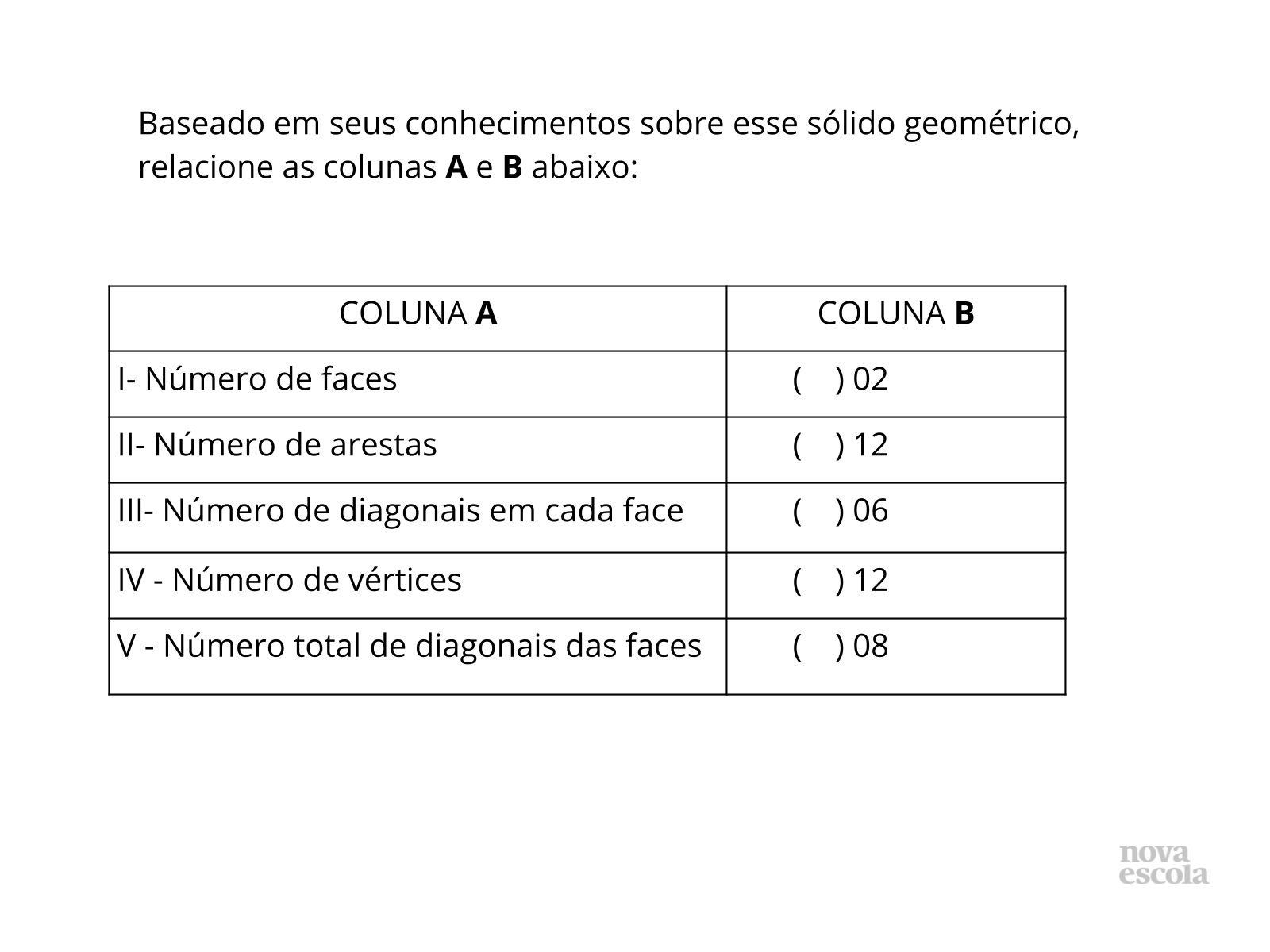
- Qual a figura plana que representa cada face do cubo?
- Em um quadrado, como se denomina o segmento que une dois vértices não adjacentes?
- Quantas diagonais possui um quadrado?
Atividade Principal
Tempo sugerido: 22 minutos. (slides 5, 6, 7, 8).
Orientações:
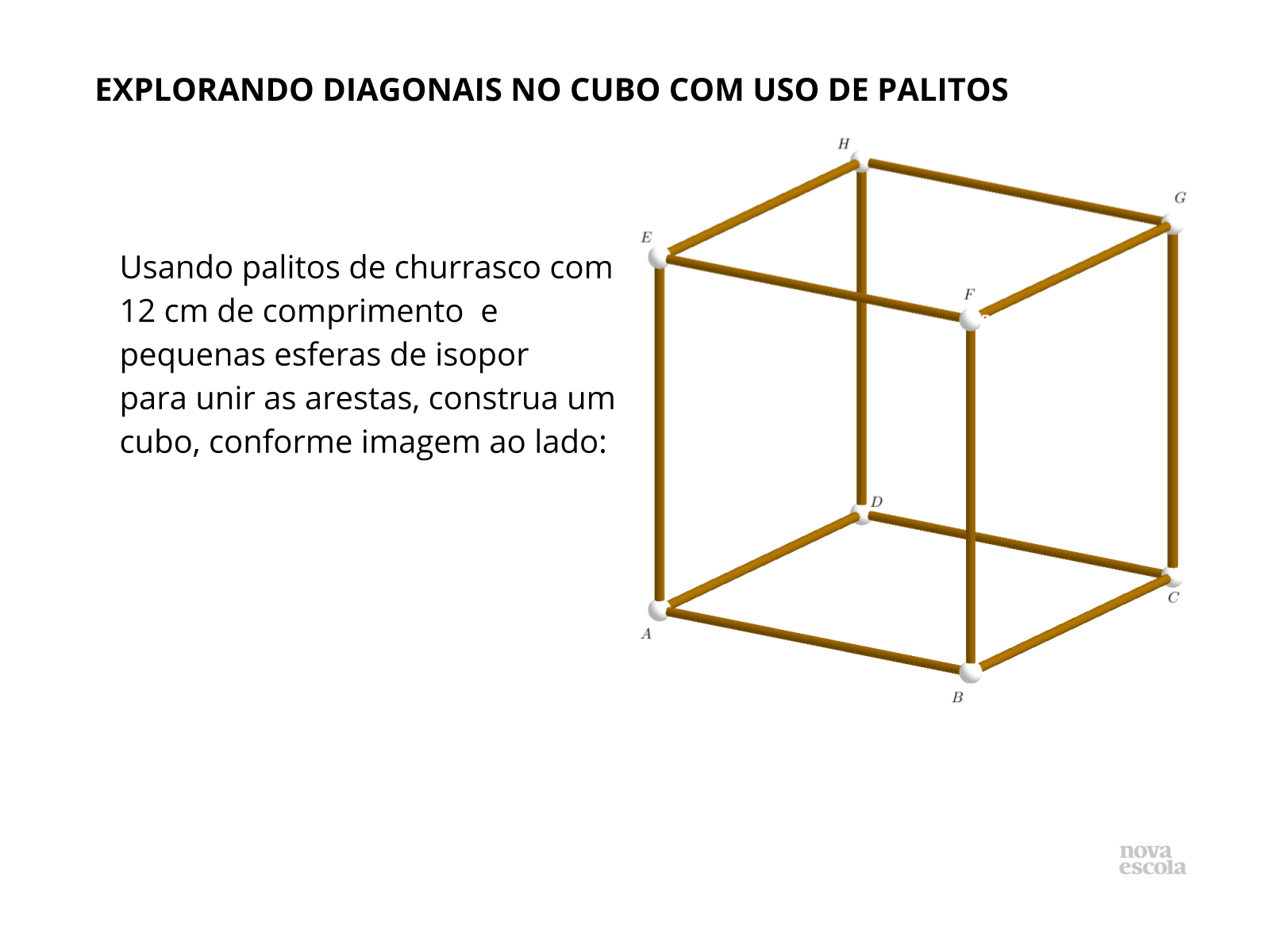
Material necessário para a construção do cubo: 12 palitos de churrasco cortados, medindo 12 cm cada, 2 palitos de churrascos com tamanho normal, para as diagonais ( em torno de 25cm), 8 esferas pequenas de isopor (para unir as arestas), estilete, régua e lápis. Disponibilize essa quantidade de material por equipe. Realize a atividade em equipes de no máximo 3 componentes, para que possam interagir e trocar ideias em torno da resolução e dessa forma construírem uma hipótese coletiva. Disponibilize a atividade impressa para os alunos, assim poderão visualizar antecipadamente o que se pretende construir e terão mais tempo para realizar as investigações em torno dos questionamentos e construírem uma conjectura para o cálculo das diagonais, principalmente para a generalização dos modelos matemáticos envolvidos.
Propósito: Utilizar o Teorema de Pitágoras para deduzir a medida das diagonais de um cubo, em função da medida do lado.
Discuta com a turma:
- Quantas arestas e quantos vértices possui um cubo?
- Qual a medida do ângulo entre dois vértices consecutivos de um cubo?
Materiais complementares para impressão:
Atividade principal
Resolução da atividade principal
Guia de intervenção
Atividade Principal

Tempo sugerido: 22 minutos. (slides 5, 6, 7, 8).
Orientações:
Disponibilize a atividade impressa para os alunos, assim terão mais tempo para realizar as investigações em torno dos questionamentos e construírem uma hipótese. Após realizarem os cálculos do comprimento de cada diagonal, oriente os alunos, com estilete, a cortarem os palitos que irão representar as respectivas diagonais, lembrando que poderá ocorrer pequenas diferenças, uma vez que, na prática, terão que adotar um valor racional como aproximação. Usando calculadora, poderão obter os valores exatos das medidas.
Propósito: Utilizar o Teorema de Pitágoras para deduzir a medida das diagonais de um cubo, em função da medida do lado.
Discuta com a turma:
- Qual é, segundo a geometria euclidiana plana, a menor distância entre dois pontos?
- Qual a relação que há entre as 3 medidas dos lados de um triângulo retângulo?
- O triângulo ACG é retângulo?
- Na prática, é possível representar de forma exata a medida de uma diagonal, representada por um número irracional?
- Como proceder nesta situação?
Atividade Principal
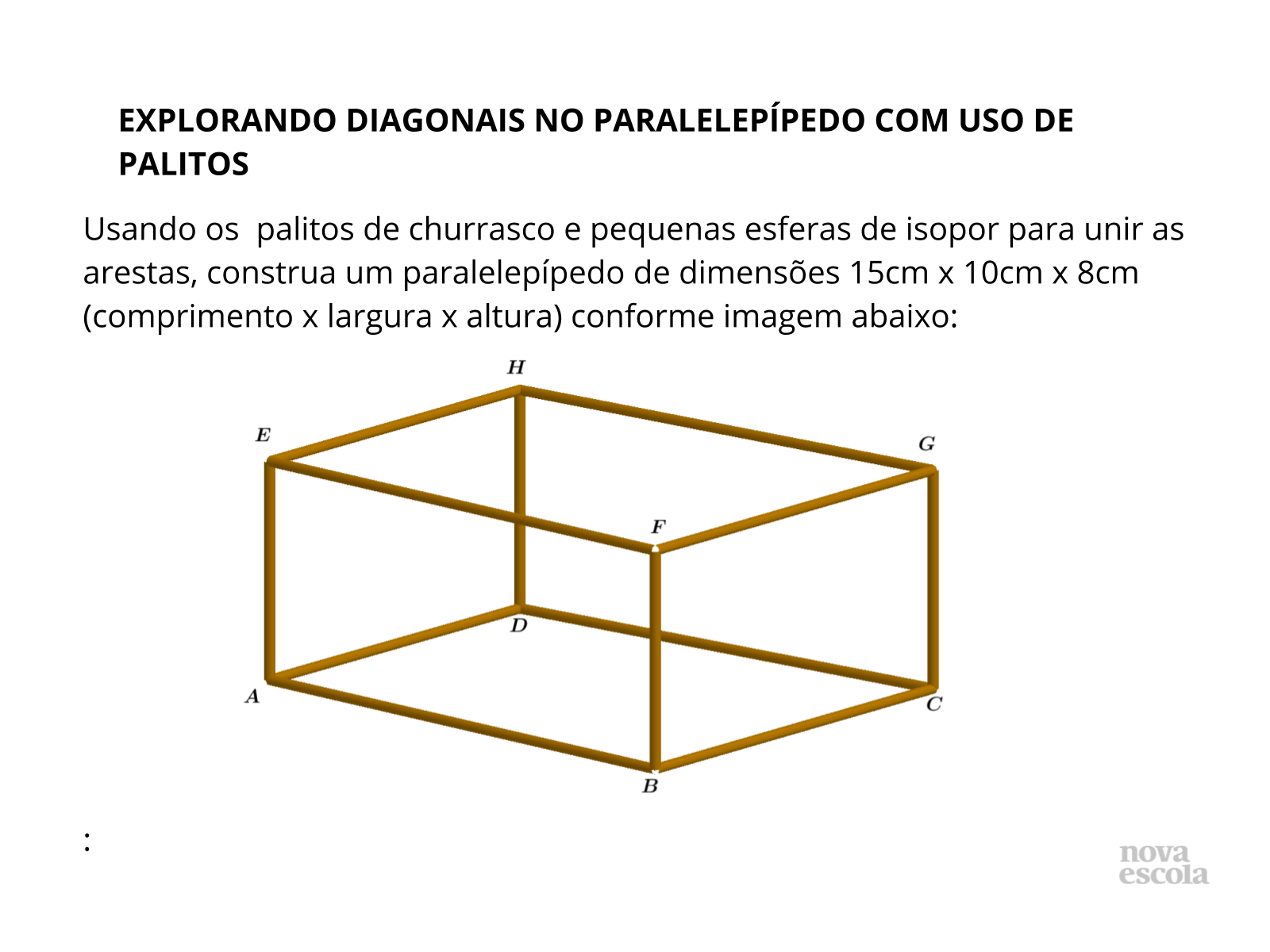
Tempo sugerido: 22 minutos. (slides 5, 6, 7, 8).
Orientações:
Material necessário: 4 palitos de churrasco medindo 15 cm, 4 palitos de churrasco medindo 10 cm, 4 palitos de churrasco medindo 8 cm, 8 esferas pequenas de isopor, estilete, régua e lápis. Disponibilize o material impresso, assim poderão visualizar antecipadamente o que se pretende construir e terão mais tempo para realizar as investigações em torno dos questionamentos e construirem uma hipótese para o cálculo das diagonais do paralelepípedo.
Propósito: Utilizar o Teorema de Pitágoras para deduzir a medida das diagonais de um paralelepípedo, em função da medida dos lados.
Discuta com a turma:
- Qual a medida do ângulo entre duas arestas consecutivas do paralelepípedo?
- Qual as diferenças entre o cubo e o paralelepípedo?
- Quantas diagonais possui cada face do paralelepípedo? Elas possuem a mesma medida?
Atividade Principal

Tempo sugerido: 22 minutos. (slides 5, 6, 7, 8).
Orientações:
Material necessário: 4 palitos de churrasco medindo 15 cm, 4 palitos de churrasco medindo 10 cm, 4 palitos de churrasco medindo 8 cm, 8 esferas pequenas de isopor, estilete, régua e lápis. Disponibilize o material impresso, assim poderão visualizar antecipadamente o que se pretende construir e terão mais tempo para realizar as investigações em torno dos questionamentos e construirem uma hipótese para o cálculo das diagonais do paralelepípedo.
Após realizarem os cálculos do comprimento de cada diagonal, oriente os alunos, com estilete, a cortarem os palitos que irão representar as respectivas diagonais, lembrando que poderá ocorrer pequenas diferenças, uma vez que, na prática, terão que adotar um valor racional como aproximação. Usando calculadora, poderão obter os valores exatos das medidas.
Discuta com a turma:
- O triângulo EFG é retângulo?
- Qual a relação que há entre as 3 medidas dos lados de um triângulo retângulo?
- O que é um modelo matemático?
- O que significa generalizar um modelo matemático?
Discussão das Soluções

Tempo sugerido: 7 minutos.
Orientações:
Estimule os alunos a exporem as dificuldades e caminhos percorridos no decorrer da atividade. É importante que eles percebam que o teorema de Pitágoras é um instrumento auxiliar e que pode ser utilizado nas mais diversas situações em que ocorra um ângulo reto em um triângulo.
Propósito: Discutir a solução e as dificuldades apresentadas no decorrer da atividade
Discuta com a turma:
- Quais os elementos matemáticos necessários para a obtenção das medidas das diagonais de um cubo?
- Você conhece alguma outra aplicação do teorema de Pitágoras?
Encerramento

Tempo sugerido: 5 minutos.
Orientações: Encerre a aula resumindo com os alunos os modelos desenvolvidos para o cubo. Optamos por não destacar os modelos obtidos para o paralelepípedo, por acreditar não haver necessidade de memorização de tais modelos, sendo mais importante a compreensão de como os mesmos podem ser obtidos pelo Teorema de Pitágoras.
Propósito: Sintetizar o que foi desenvolvido na aula.
Discuta com a turma:
- Será sempre necessário aplicar o Teorema de Pitágoras para calcular as medidas das diagonais de um cubo?
- O que é necessário para se obter as medidas das diagonais de um paralelepípedo?
Raio X
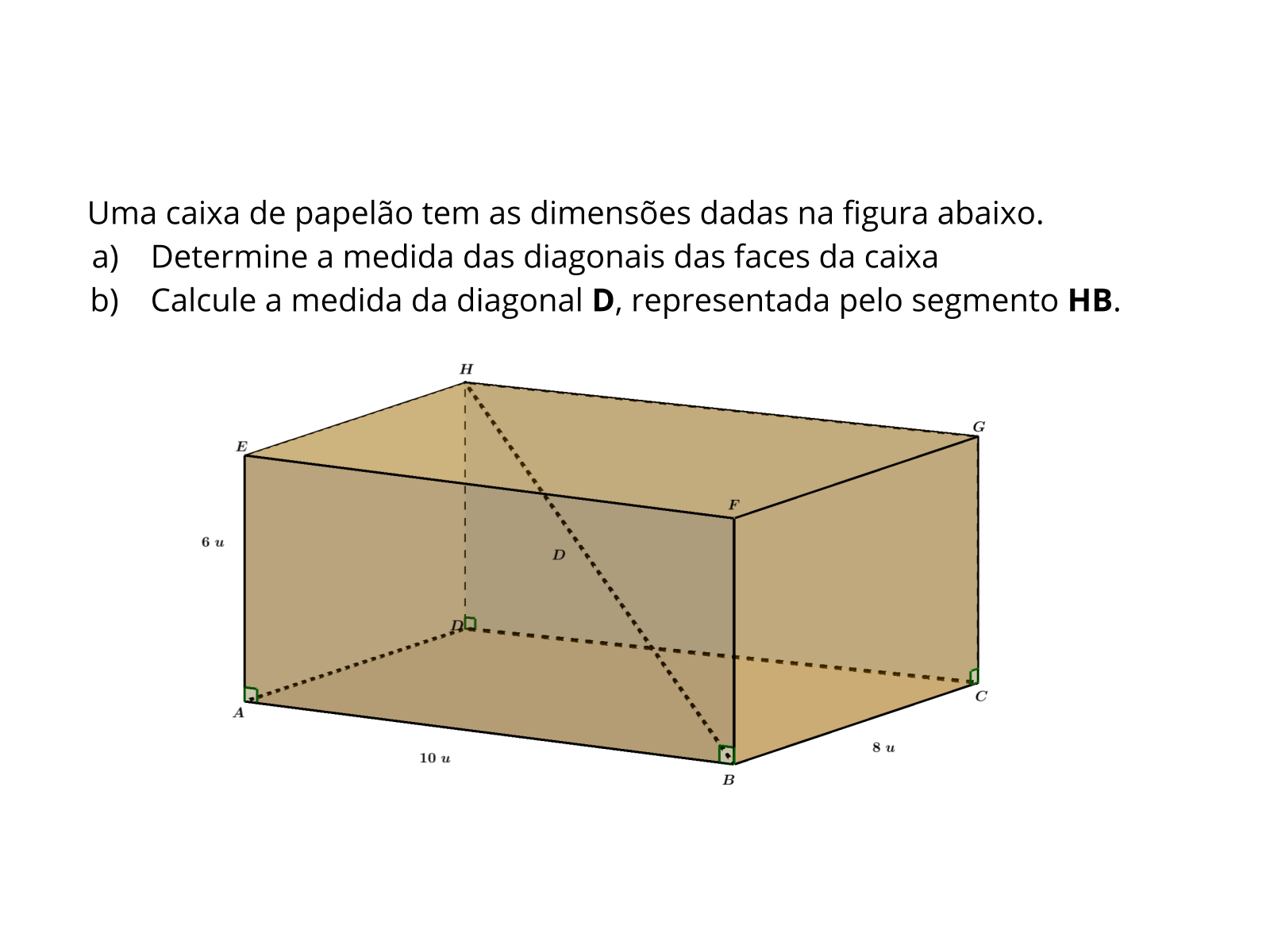
Tempo sugerido: 6 minutos.
Orientações: Caso os alunos apresentem dificuldades em visualizar a diagonal D, o professor poderá lançar mão de material concreto, como um caixa de sapatos, por exemplo. Outra opção e mostrar essas diagonais em uma construção em um software, como o Geogebra.
Propósito: Avaliar se os objetivos da aula foram alcançados
Discussão com a turma:
- Quantas diagonais possui cada face da caixa?
- Essas diagonais têm a mesma medida?
- Qual a medida do ângulo HDB?
- O que é necessário para se calcular a diagonal D, da caixa?
Materiais complementares para impressão:
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar
 Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.