Atividade Principal
Plano de Aula
Plano de aula: Matemática e Geografia, um diálogo entre Medidas.
Plano 9 de uma sequência de 10 planos. Veja todos os planos sobre Grandezas e Medidas
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Rosélia Sezerino Fenner
Mentor: Fabio Menezes da Silva
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF05MA19) Resolver e elaborar problemas envolvendo medidas das grandezas; comprimento, área massa, tempo, temperatura e capacidade, recorrendo transformações entre as unidades mais usuais em contextos socioculturais.
Objetivos específicos
Estimar e calcular medidas, tendo como objeto de estudo o espaço geográfico, através do auxílio da Matemática.
Conceito-chave
Medidas de comprimento
Recursos necessários
- Atividades impressas em folhas, coladas no caderno ou não;
- Lápis;
- Caderno;
- Borracha;
- Livros didáticos de Geografia;
- Aparelho de tablet, celular ou outro dispositivo móvel que tenha baixado um aplicativo para uso do GPS, ou, um equipamento, GPS (opcional).
Habilidades BNCC:
Objetivos de aprendizagem
Estimar e calcular medidas, tendo como objeto de estudo o espaço geográfico, através do auxílio da Matemática.
Resumo da aula
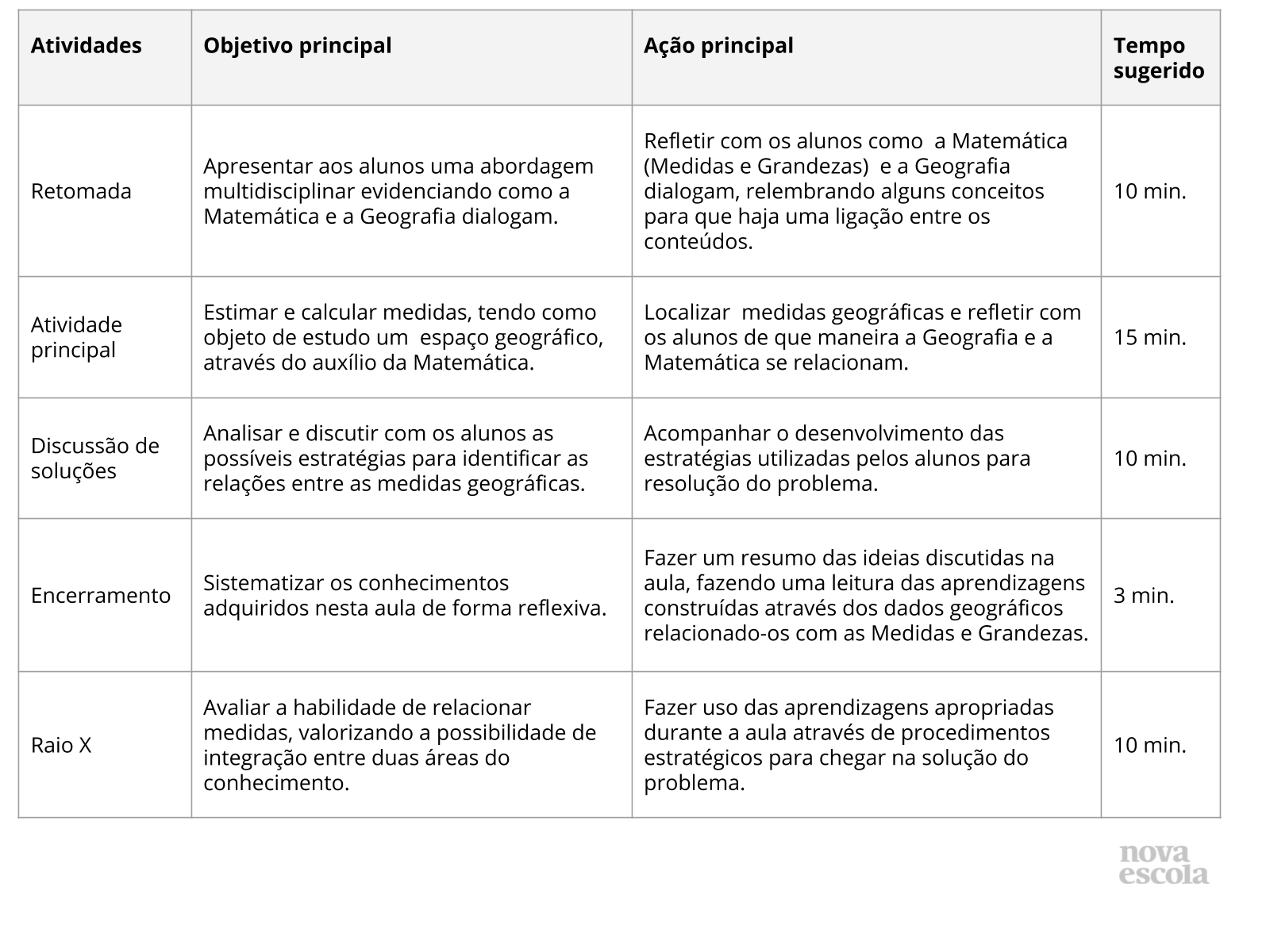 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para turma.
Propósito: Compartilhar com a turma o objetivo da aula.
Retomada

Tempo sugerido: 10 min (slide 3 e 4).
Orientação: Pegue um livro de Geografia, leia para os alunos alguma informação sobre um assunto que esteja relacionado com a Matemática. Pergunte se alguma coisa chamou a atenção, por que usar uma informação do livro de Geografia se a aula é de Matemática? Espera-se que os alunos comentem que nas informações também são apresentados conceitos matemáticos.
Projete o slide e peça que os alunos leiam a fala dos balões. Se preferir, apenas leia para os alunos o texto dos balões.
Propósito: Apresentar aos alunos uma abordagem multidisciplinar evidenciando como a Matemática e a Geografia dialogam
Discuta com a turma
- Vocês já haviam percebido essa ligação que há entre a Geografia e Matemática?
- Em quais outras situações que vocês lembram que as Medidas e Grandezas estão presentes na Geografia?
- E com outras disciplinas, a Matemática, mais especificamente as “Medidas” também está interligada? De que forma?
Retomada

Tempo sugerido: 10 minutos (slides 3 e 4)
Orientação: Projete o slide e discuta coletivamente com a turma as informações referentes a dados geográficos, porém, que envolvem o tema “Medidas”. Faça com que reflitam que a Geografia oferece uma enorme possibilidade de integração, pelo fato de ter como objeto de estudo o espaço geográfico, construído ou natural e, a Matemática está relacionada a tudo que encontramos na natureza.
Se preferir, proponha aos alunos buscarem outras informações no livro didático que apresentem dados matemáticos que envolvam as “Medidas”, conforme exemplos nos slide.
Discuta com a turma os dados matemáticos, as unidades de medidas que estão nos textos, o que elas “medem”, que instrumentos são utilizados para fazer as medições, qual a relação que há entre as grandezas “km² e o metro”, quantos quilogramas que correspondem a toneladas, a temperatura 44,7 ºC é parecida com a temperatura da sua região? Estas e outras observações poderão ser exploradas, a fim de retomar alguns conceitos sobre as Medidas.
Propósito: Refletir com os alunos como a Matemática (Medidas e Grandeza) e a Geografia dialogam, relembrando alguns conceitos para que haja uma ligação entre os conteúdos.
Discuta com a turma:
- Quais são as unidades de medidas que vocês identificaram nas falas dos personagens?
- Com o que vocês imaginam que a altura da montanha Everest pode ser comparada?
- Que temperatura você estima que está o clima da nossa cidade, será que está próxima aos 44 ºC?
- Uma tonelada corresponde a quantos quilogramas?
- Em 58 milhões de toneladas, quantos quilogramas vocês calculam que pode ter?
- Por que as estimativas variaram de uma dupla para outra?
- A medida da superfície ocupada pela montanha Everest é maior ou menor se compararmos à medida da superfície ocupada pelo território brasileiro?
- Por que a medida da superfície do Brasil é determinada em km²?
- Poderia ser indicada em metros?
Atividade Principal

Tempo sugerido: 15 minutos (slides 5 e 6).
Orientação: Projete o slide e peça a dois alunos para que leiam o diálogo entre os dois personagens. Questione a turma sobre o que sabem a respeito do assunto, será que é possível saber a medida exata de uma montanha? Por que os geógrafos e aviadores têm interesses sobre a exatidão nessas medidas? Há algum conceito matemático que explique esse interesse?
Pergunte qual a diferença entre altitude e altura. A definição desses conceitos pode ser ampliado nas aulas de Geografia, neste site você encontra algumas informações sobre esse assunto. Neste outro site, você pode consultar mais informações a respeito das novas medições que foram realizadas, tem muita coisa interessante por lá.
Questione ainda, quanto eles estimam ser a altitude que os aviões voam (cerca de 11 000 m) e se há algo relacionado ao fato dos aviadores saberem a altitude exata das montanhas.
Questione-os sobre o uso de instrumentos precisos para medição. No caso das montanhas, que instrumento é usado para medir a altura? Pergunte ainda se sabem como eram feitas as medições antes das novas tecnologias, o GPS. As medições eram realizadas através de um aparelho chamado “Barômetro”, não fornecia os dados com precisão. Se possível, faça uma breve explanação sobre o uso deste “sistema”, que é utilizado para localizar endereços, pontos específicos e determinados posicionamentos sobre a superfície terrestre). Segue uma sugestão de site de pesquisa sobre o GPS.
Propósito: Refletir de que forma a Matemática, em especial o eixo “Medidas” está presente em outras áreas do conhecimento.
Discuta com a turma:
- Vocês acham importante saber a medida exata das coisas? Por quê?
- Mas, quando não se tem um aparelho para fazer a medição, qual habilidade temos de ter desenvolvido em caso de necessidade? (estimativa).
- A altitude que um avião pode voar, vocês consideram alto ou baixo?
- Se comparar com a altura de uma pessoa de 1 metro de altura, quantas vezes precisaria para completar mais ou menos a altura que o avião voa?
Atividade Principal

Tempo sugerido: 15 minutos (slides 5 e 6).
Orientação: Organize a turma em duplas, trios ou grupos de 4 integrantes. Aproveite para explorar as possibilidades de divisão da turma de modo que formem conjuntos com o mesmo número de integrantes. Distribua uma cópia da atividade, ou se preferir pode ser escrita no quadro ou mesmo fazer um auto ditado da atividade.
Propicie um ambiente agradável, de modo que os alunos possam se envolver na atividade. Faça inicialmente uma leitura coletiva do problema. Oriente-os para mais uma leitura, dessa vez individualmente, para então dar início às discussões com seus colegas do grupo.
Observe se todos estão tendo oportunidade de sugerir uma estratégia. Desafie-os a resolver o problema apresentando mais de uma estratégia. Ao perceber que algum aluno está tendo dificuldades, não conseguindo acompanhar o ritmo dos demais do grupo, auxilie-o, porém, faça-o refletir, provoque-o através de boas perguntas de modo que ele avance. Consulte o guia de intervenções, disponível nos materiais complementares, lá você encontra sugestões de intervenções a serem feitas com os alunos. No item a seguir você também encontra sugestões de perguntas que levam o aluno a refletir e pensar matematicamente sobre a solução do problema.
Certifique-se que todos os grupos concluíram a atividade através de uma estratégia pessoal, sem focar em métodos de memorização e sim, aqueles possam garantir a aprendizagem e torná-la significativa.
Socialize então, as estratégias dos grupos, o modo como cada um pensou, por onde começou a resolver. Convide alguns alunos a compartilhar com a turma a estratégias pessoais que usaram para resolver o problema. Compare com as soluções dos outros grupos. Por fim, passe para a série de slides que apresentam possíveis soluções para o problema, discuta com a turma, explorando todas as informações.
Propósito: Estimar e calcular medidas, através de estratégias pessoais, tendo como objeto de estudo o espaço geográfico, através do auxílio da Matemática.
Discuta com a turma:
- O que vocês acham sobre a unidade de medida usada para determinar a altitude da montanha, por que foi usado o metro e não quilômetro?
- Vocês conseguem imaginar o quanto esse pico é alto?
- Em relação à medida que aumentou (152cm), é muito ou é pouco? É mais que um metro ou menos?
- Quanto a mais que um metro?
- A medida que passou de um metro corresponde a que parte do metro mais ou menos?
- Então, como podemos dizer de outra forma a leitura dessa medida?
- Se o aumento corresponde mais de um metro, de que maneira podemos fazer o registro dessa medida? (1,52m)
- A que podemos comparar esse aumento? (altura de uma pessoa).
- Pense em um prédio de 30 andares, que tem aproximadamente 155 m de altura. O Pico da Neblina tem altura equivalente à de quantos prédios de 30 andares, um em cima do outro?
- Se a medida 2 995,30m fosse usada para representar uma distância, e não mais uma altura, qual seria a unidade mais adequada para representá-la?
- Quantos quilômetros aproximadamente poderíamos considerar essa distância?
- Agora, analisando essa medida como uma distância, vocês acham que é um percurso longo ou curto?
- A que podemos comparar essa distância?
- Por que houve esse aumento na altura da montanha, será que ela cresceu?
- O uso de instrumentos que medem com mais exatidão podem ser o motivo da descoberta desse aumento na medida?
Materiais complementares
Discussão da solução

Tempo sugerido: 10 minutos.
Orientação: Assim que os alunos concluírem suas estratégias de cálculo e estimativas, socialize as soluções que encontraram, registrando e comparando um resultado ao outro.
Projete a tabela no multimídia somente após a socialização das ideias dos alunos. Se preferir, o professor pode fazer uso do quadro para registrar as ideias contidas nos slides para serem debatidas. Compare as soluções, para que os alunos percebam que é possível resolver um problema de diversas formas.
Inicialmente, reflita com os alunos que o uso de novas tecnologias têm sido um importante recurso para aprimoramento das informações, o resultado reflete em novos dados estatísticos. Através dessa atividade, os alunos poderão ainda compreender a relação que existe entre as unidades de medidas de comprimento (cm/m). Discuta essa relação entre as unidades, é possível somar ou subtrair duas unidades de grandezas diferentes? Relembre se necessário a unidade padrão do metro, quantos centímetros “cabem” em um metro.
Propósito: Realizar um debate das ideias discutidas até o momento, levando-os a refletir sobre as estratégias pessoais utilizadas nas resoluções e as diferentes respostas encontradas. Utilize o quadro para exemplificar uma situação onde preciso subtrair duas medidas de grandezas diferentes. Explore todo o processo de transformação.
Discuta com a turma:
- O que deve ser feito quando tenho duas grandezas diferentes e quero fazer uma operação de subtração?
Discussão da solução
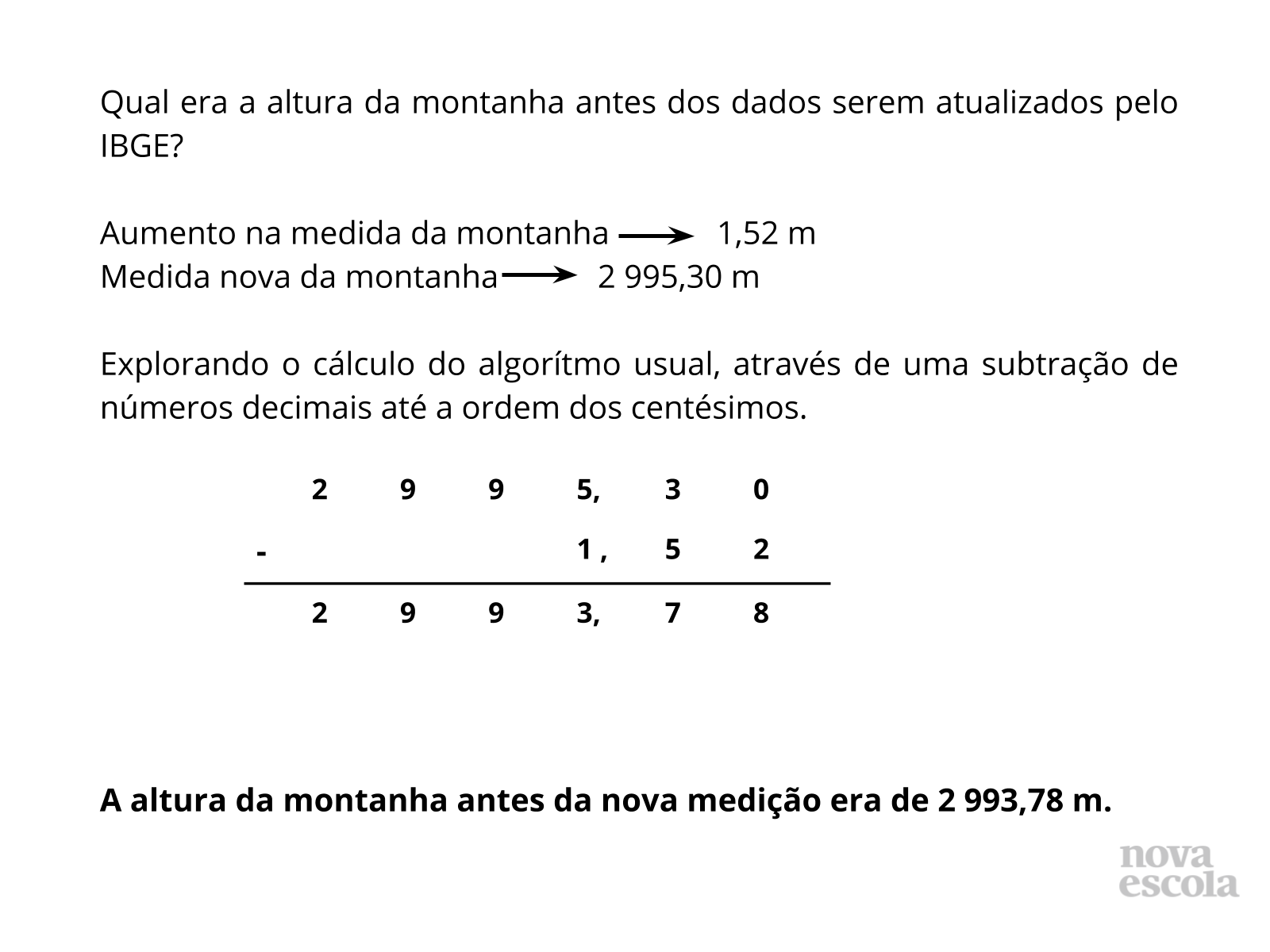
Tempo sugerido: 10 minutos (slides 8 à 11)
Propósito: Discutir com a turma, diferentes estratégias de resolução, levando os alunos à reflexão sobre os passos executados nas etapas do algoritmo.
Orientação: Amplie a discussão dessa estratégia de solução. A aprendizagem do algoritmo usual vem complementar e oferecer um procedimento de reconhecido uso social. Lembrando que é importante o aprendizado do algoritmo usual ser acompanhado da compreensão da estrutura do nosso sistema de numeração, que fundamenta as etapas do procedimento. É importante também os alunos relacionarem os algarismos de cada ordens com a unidade de medida (1 décimo com 10 cm, 3 décimos com 30 cm, etc.)
Discussão da solução
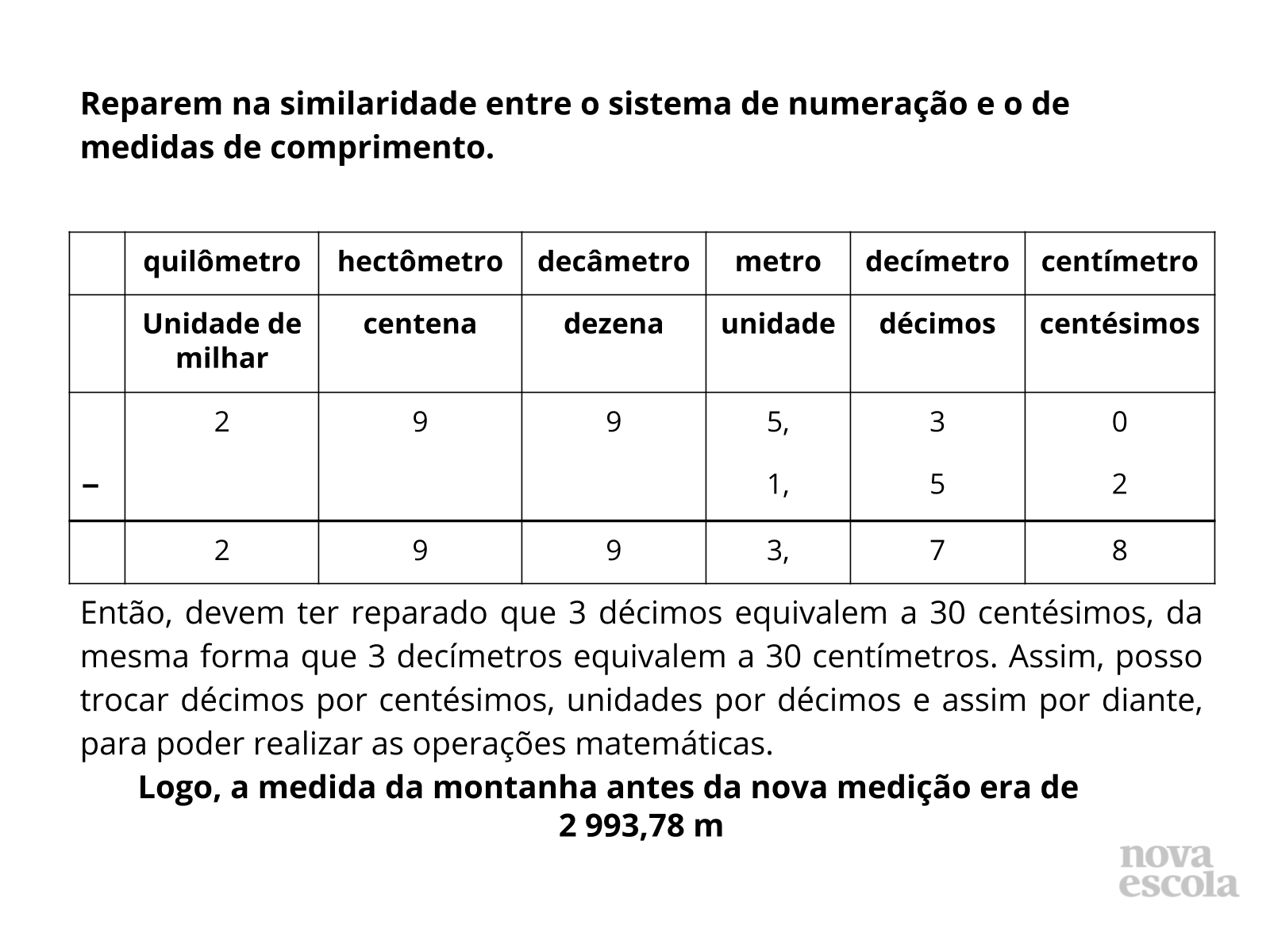
Tempo sugerido: 10 minutos (slides 8 à 11)
Propósito: Discutir com os alunos diferentes estratégias de solução explorando o cálculo através do quadro de ordens.
Orientação: O modelo do “quadro de ordens” pode ser um recurso para que o aluno compreenda as transformações, porém, deve ser ressaltado que as unidades de medida de comprimento como hectômetro, decâmetro, decímetro, são pouco usadas no dia a dia, mas a presença dessas unidades no quadro permitirá ao aluno compreender a equivalência entre as unidades de medida do sistema métrico decimal e as ordens do sistema de numeração decimal.
Discussão da solução

Tempo sugerido: 10 minutos (slides 8 à 11)
Propósito: Discutir com os alunos a solução do problema através do processo de decomposição das unidades de medida.
Orientação: Retome com os alunos que o centímetro é a centésima parte do metro, isto é, 1 cm = 1/100 m ou, 0,01 m. Assim, 152 cm correspondem a 1,52 m. Ressalte também que neste caso foi realizada a decomposição de 5 metros em centímetros (5 x 100 = 500), assim é possível subtrair as grandezas em centímetros (530 cm - 152 cm = 378 cm). Em 378 centímetros há 3 metros inteiros mais 78 centímetros (0,78).
Discussão da solução

Tempo sugerido: 10 minutos (slides 8 à 11)
Propósito: Discutir com os alunos diferentes estratégias de solução, através do processo de transformação das unidades de medida de comprimento.
Orientação: Para realizar as transformações, retome com os alunos que o centímetro é a centésima parte do metro (1 m = 100 cm) e o metro é a milésima parte do quilômetro ( 1 km = 1 000 m). Se julgar necessário, explore passo a passo o processo registrando no quadro com o acompanhamento e auxílio dos alunos.
Encerramento

Tempo sugerido: 3 minutos
Propósito: Sistematizar os conhecimentos adquiridos nesta aula de forma reflexiva.
Orientação: Fazer um resumo das ideias discutidas na aula, fazendo uma leitura das aprendizagens construídas através dos dados geográficos relacionado-os com as Medidas e Grandezas.
Raio X
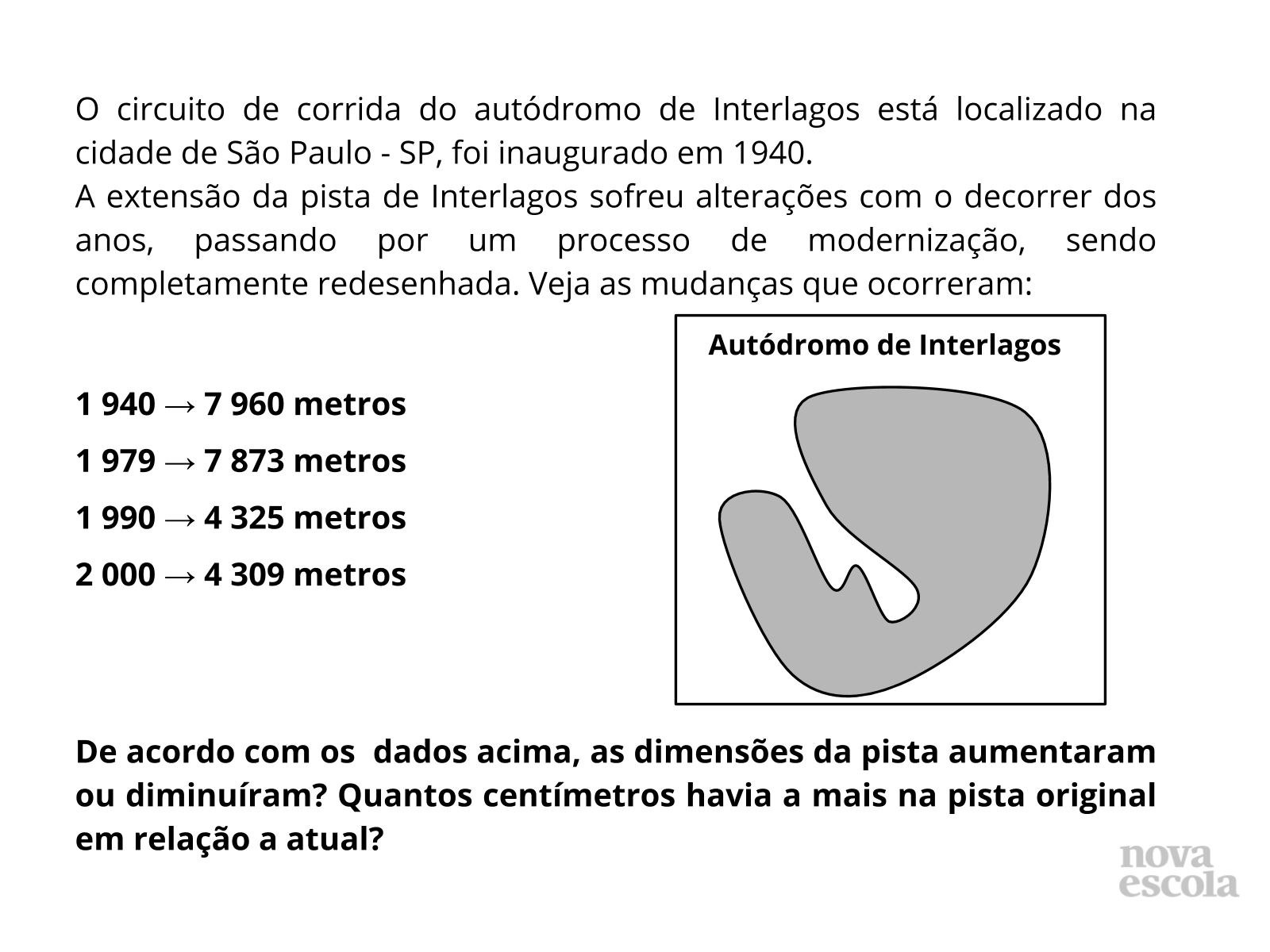
Tempo sugerido: 10 minutos
Propósito: Avaliar a habilidade de relacionar medidas, valorizando a possibilidade de integração entre duas áreas do conhecimento.
Orientação: O Raio x é o momento de avaliar se os alunos estão fazendo uso das aprendizagens apropriadas durante a aula, através de procedimentos estratégicos para chegar na solução do problema.
Para que o professor possa avaliar se os alunos estão dominando os conceitos trabalhados durante a aula, recomenda-se que a atividade seja realizada individualmente, usando estratégias pessoais de solução, assim, o professor poderá analisar quais conceitos ainda será necessário retomar em outras aulas, garantindo assim a aprendizagem.
Quando todos concluírem, socialize as diferentes formas de solução que os alunos desenvolveram, sempre instigando o aluno a refletir sobre o resultado que encontrou.
Materiais complementares
Para os Alunos
Para o Professor
Sugestão de adaptação para ensino remoto
Código do plano MAT5_20GRM09
Recursos
- Necessários: -
- Opcionais: -
Para este plano, foque na etapa Retomada, Atividade principal e Discussão das soluções
Retomada
Professor(a), você pode realizar a Retomada deste plano com seus alunos, seja em uma aula síncrona ou assíncrona. Compartilhe com a turma os slides presentes nesta atividade e solicite que reflitam sobre as situações de medida ali colocadas. Caso a aula esteja ocorrendo de forma síncrona, permita que os alunos exponham suas reflexões e caso esteja ocorrendo de forma assíncrona, os estudantes podem gravar vídeos ou áudios. Compartilhe, em formato de texto ou verbalizando, os questionamentos presentes no “Discuta com a turma” para fomentar as discussões, você pode incluir perguntas sobre o tempo da quarentena/isolamento social.
Atividade principal
Professor(a), compartilhe com a turma os slides presentes nesta atividade e solicite que tentem resolver o problema. Você pode encontrar o documento com a atividade aqui: https://nova-escola-producao.s3.amazonaws.com/AbG83mjRFn38BHzdyCrz7GSjyY6nkKacNYjNe68y4HjBcM3QVEVSZMBTy9T7/ativprinc-mat5-20grm09.pdf. Compartilhe, em formato de texto ou verbalizando, os questionamentos presentes no “Discuta com a turma”. Caso a aula esteja ocorrendo de forma síncrona, permita que os alunos exponham suas resoluções e caso esteja ocorrendo de forma assíncrona os estudantes podem enviar suas resoluções/explicações em formato de texto ou áudio. Caso seja possível mostre fotos do Pico da Neblina para a turma.
Discussão das soluções
Professor(a), compartilhe com a turma as considerações presentes nesta etapa do plano de aula. Deixar para os alunos a leitura e interpretação dos slides dessa etapa da aula pode confundi-los. Então, caso a aula esteja ocorrendo de forma síncrona, sugerimos que você verbalize cada etapa das resoluções mostrando um slide por vez. Caso a aula esteja ocorrendo de forma assíncrona, você pode gravar um vídeo mostrando as soluções e refletindo sobre as estratégias adotadas. Segue uma sugestão de atividade que pode ser utilizada na aula e fomentar a discussão e realizar conversões: https://br.ixl.com/math/5-ano/compare-e-converta-as-unidades-de-comprimento
Raio X
O problema proposto no Raio X pode ser enviado para os alunos e solicitado como uma “tarefa” a ser entregue em momento a ser combinado com a turma.
Convite às famílias
Professor(a), sugira que os alunos socializem com seus familiares o que refletiram nesta aula sobre medidas no espaço geográfico. Você pode sugerir que eles dialoguem com seus familiares sobre o possível lugar mais alto que conheceram. Eles podem realizar uma busca na internet para saber a altitude dos lugares e compararem posteriormente com seus colegas de turma.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Rosélia Sezerino Fenner
Mentor: Fabio Menezes da Silva
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF05MA19) Resolver e elaborar problemas envolvendo medidas das grandezas; comprimento, área massa, tempo, temperatura e capacidade, recorrendo transformações entre as unidades mais usuais em contextos socioculturais.
Objetivos específicos
Estimar e calcular medidas, tendo como objeto de estudo o espaço geográfico, através do auxílio da Matemática.
Conceito-chave
Medidas de comprimento
Recursos necessários
- Atividades impressas em folhas, coladas no caderno ou não;
- Lápis;
- Caderno;
- Borracha;
- Livros didáticos de Geografia;
- Aparelho de tablet, celular ou outro dispositivo móvel que tenha baixado um aplicativo para uso do GPS, ou, um equipamento, GPS (opcional).

















