Sugestão de adaptação para ensino remoto
Código do plano (MAT9_16GEO05)
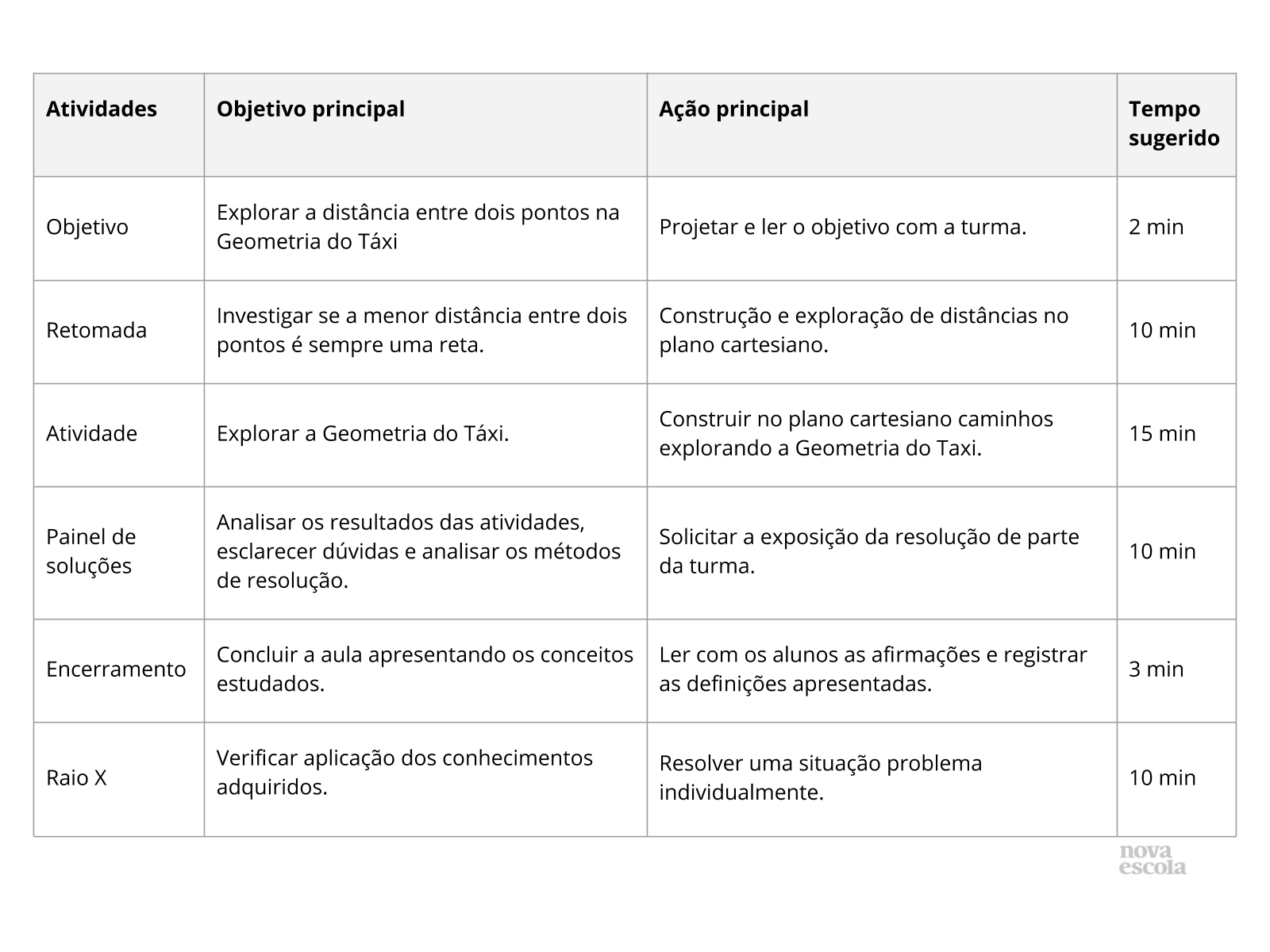
Ferramentas sugeridas
- Essenciais: Alguma rede social (Whatsapp, Facebook, etc.) régua e papel para anotações.
- Optativas: Calculadora.
Aquecimento
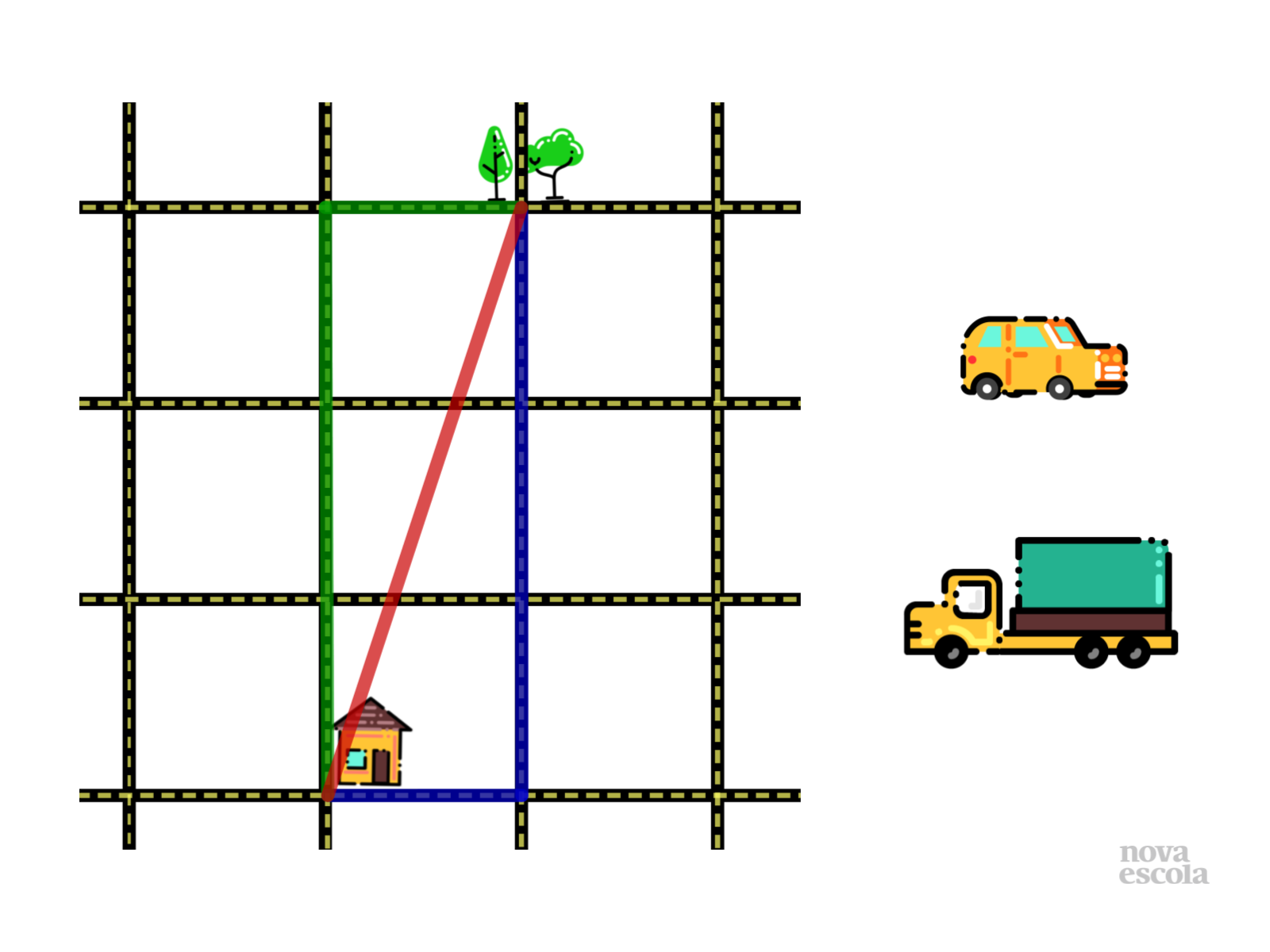
- Pela rede social escolhida, inicie esse contato questionando se, dentro de uma cidade, a menor distância que pode ser percorrida entre dois lugares é sempre uma reta.
- Dentre as repostas, mostre que muitas vezes precisamos virar várias esquinas e seguir pelas ruas existentes para que possamos atingir nosso objetivo. E que esse é o princípio do pensamento de uma nova geometria: a Geometria do Taxista ou Geometria do Táxi.
Atividade principal
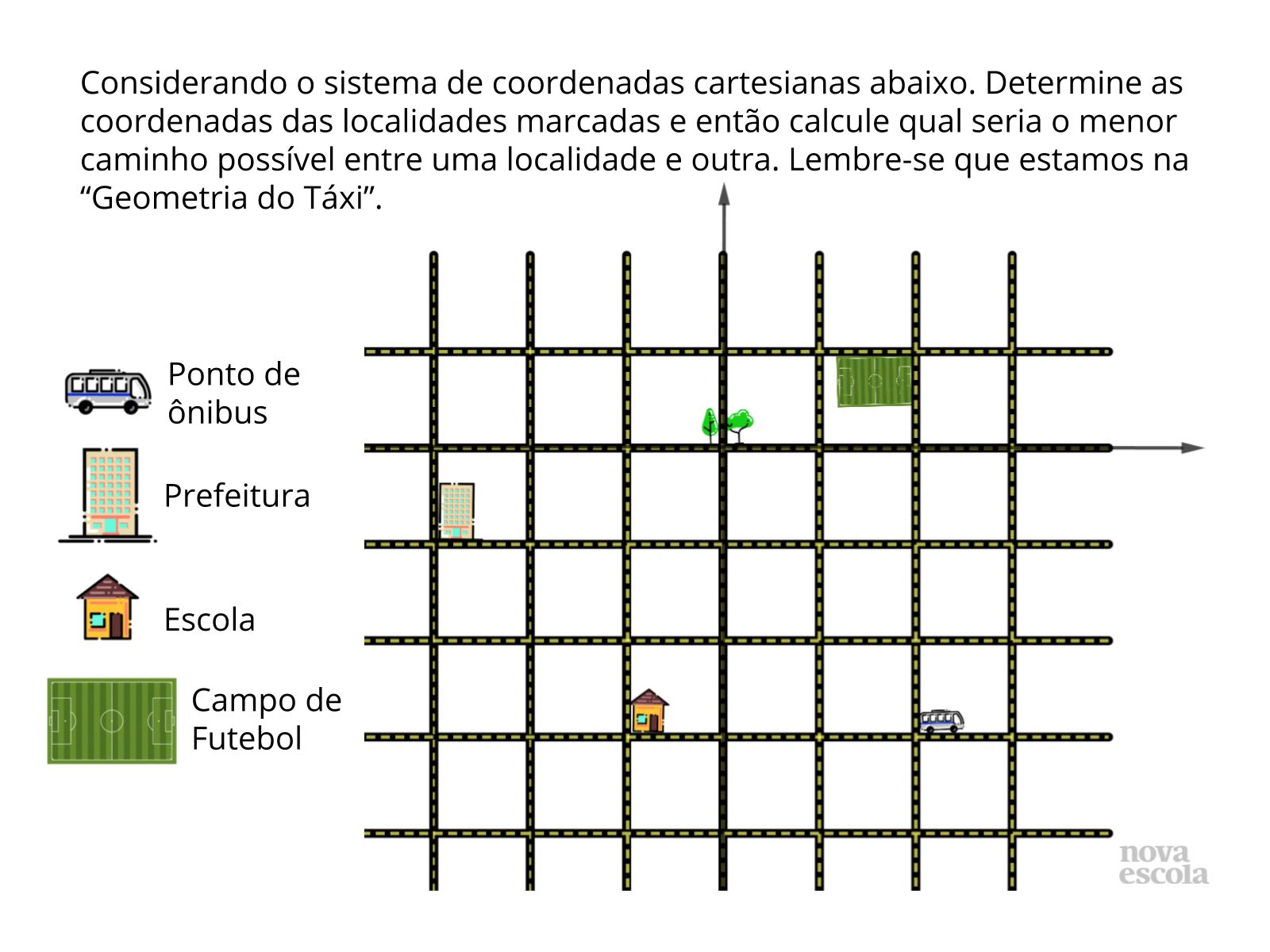
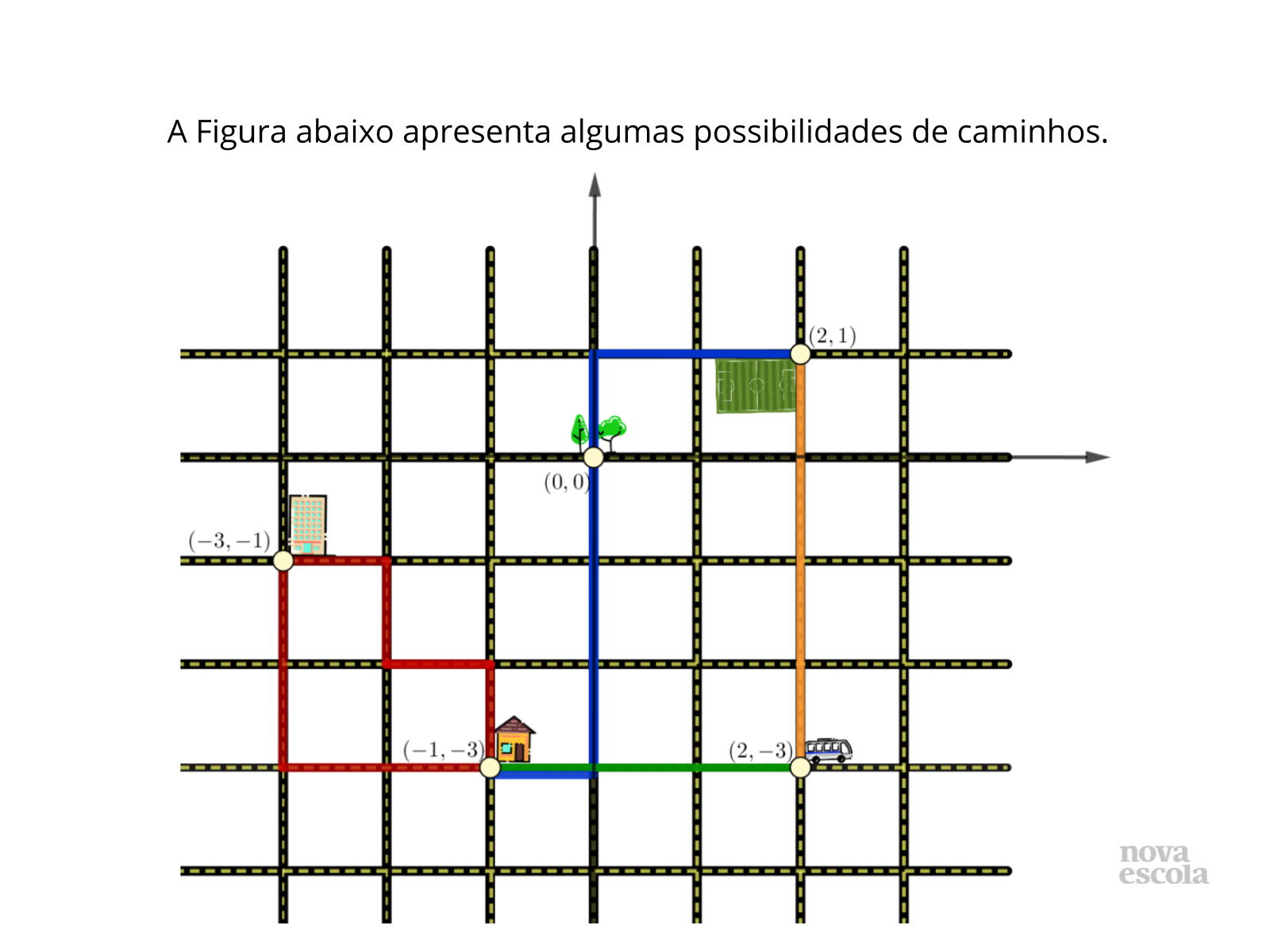
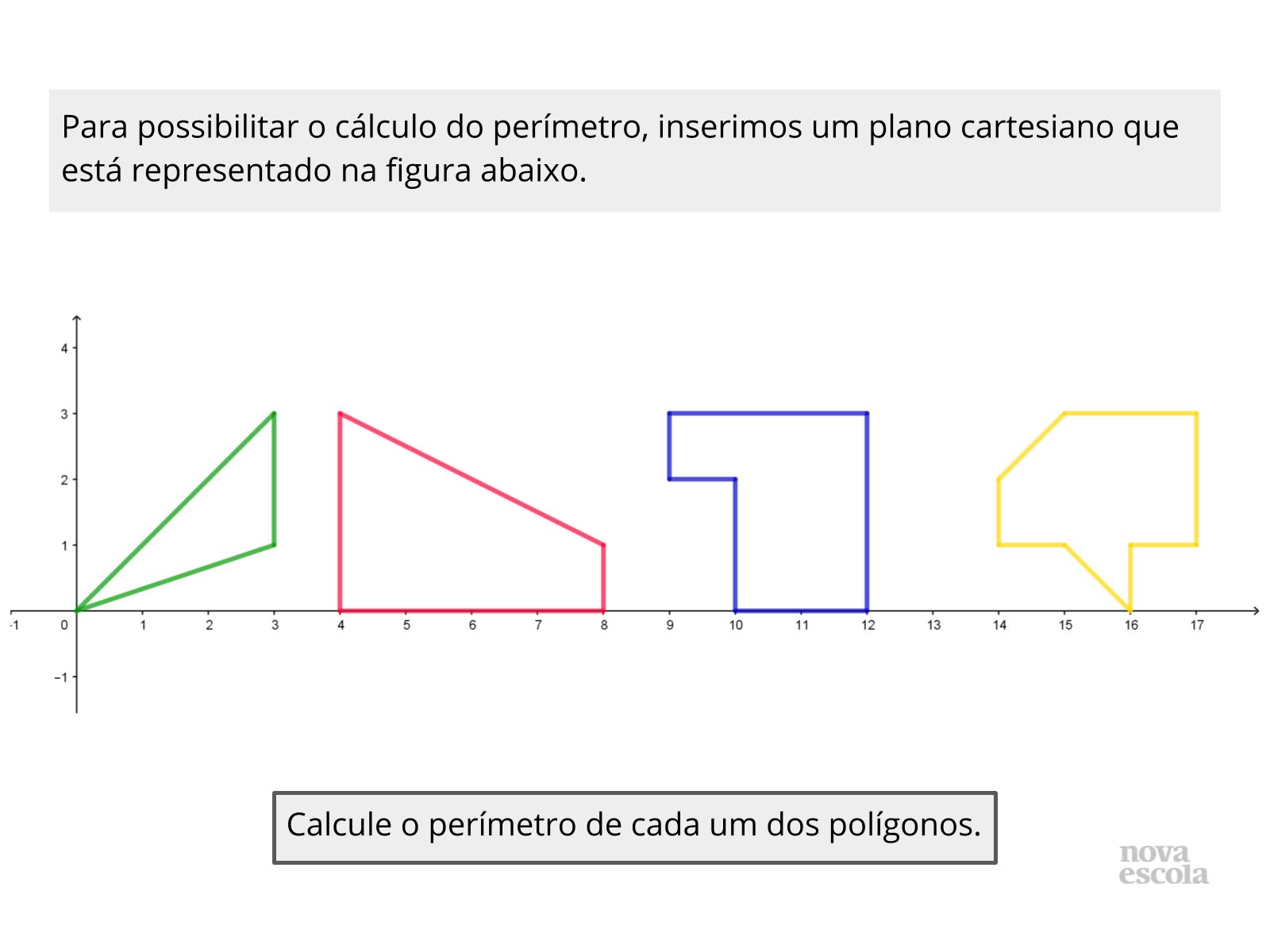
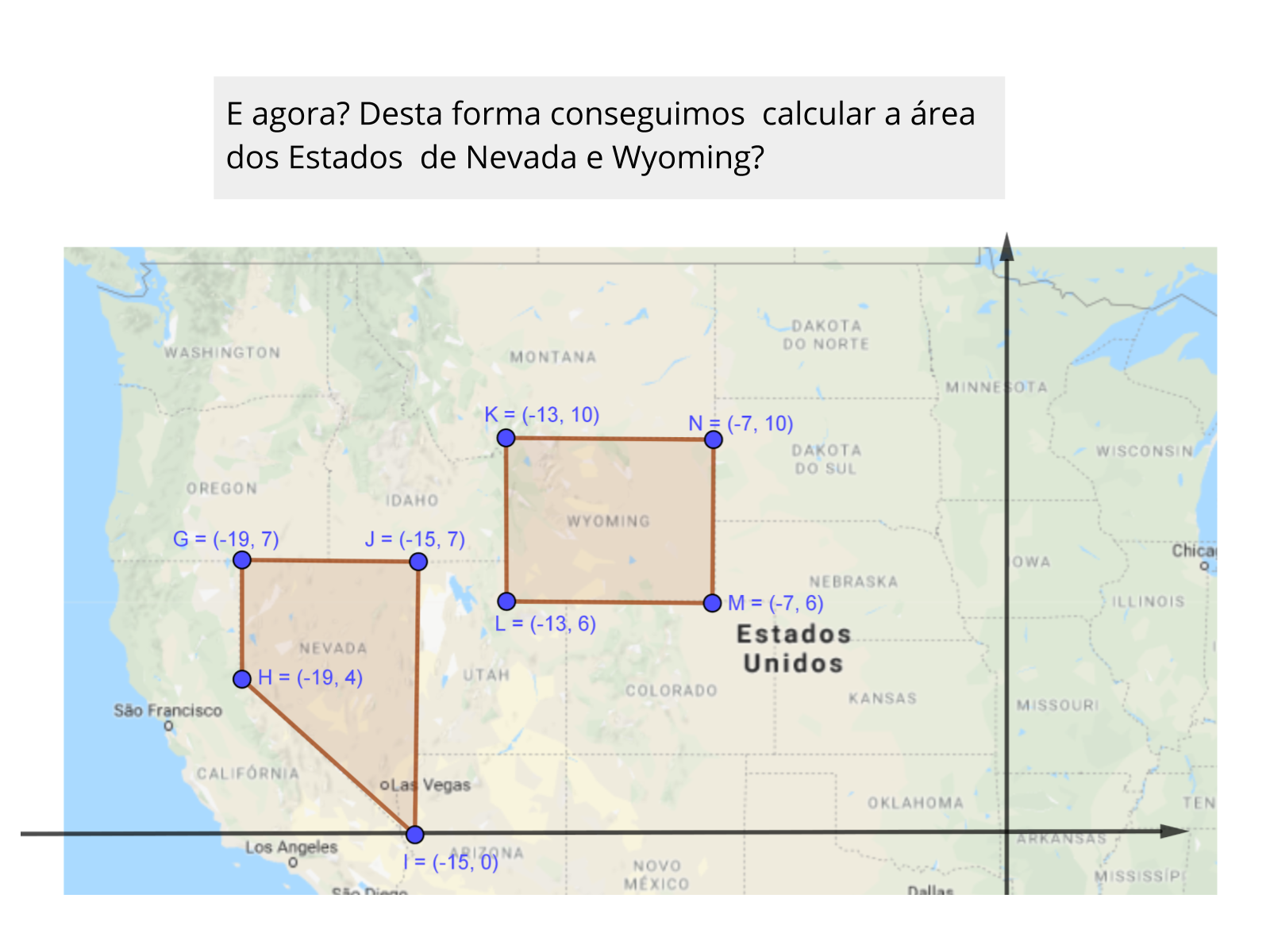
Para essa atividade, entendemos ser melhor pedir para usarem papel quadriculado ou imprimirem a imagem do plano que você poderá mandar pela rede social escolhida. Se houver uma impossibilidade de impressão, que seja disponibilizado com antecedência folhas com essas malhas quadriculadas e as imagens constantes no plano original na unidade escolar.
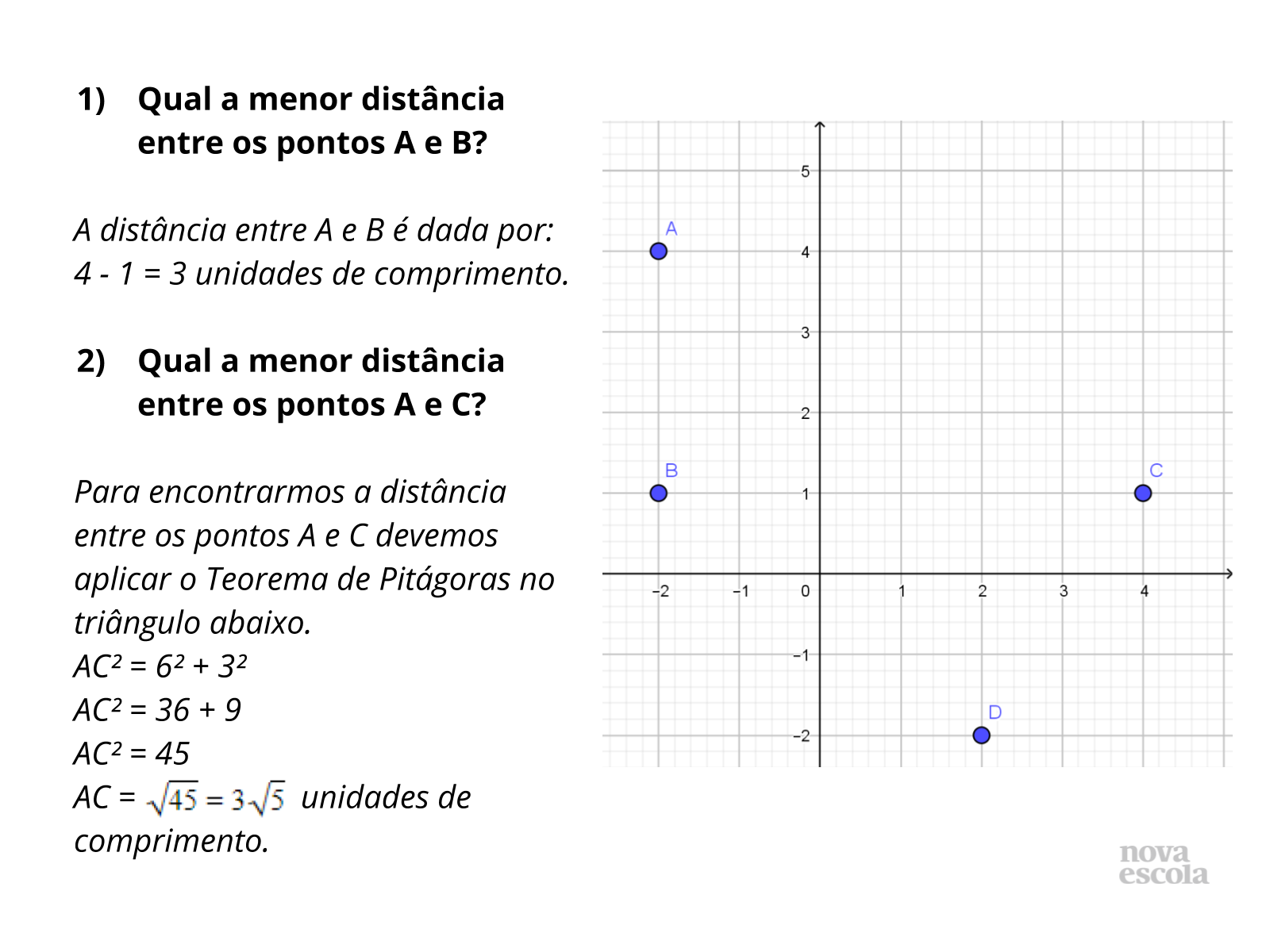
- Determine que tentem calcular a distância a ser percorrida e compará-la com a distância em linha reta daquilo que é pedido pelo plano.
- As perguntas sobre essa atividade podem ser reorganizadas em:
a) Será que existe mais de um caminho para chegar onde se quer?
b) Mas será que existe mais de um caminho que seja o menor possível?
Discussão das soluções
- Na discussão das soluções, reforce a ideia de que há geometrias diferentes e servem a diferentes propósitos com diferentes resultados para distâncias, pois são relativos a caminhos diferentes.
Sistematização e encerramento
- Faça uma sistematização, destacando que quando falamos em distância, na geometria, é preciso saber de qual geometria estamos nos referindo, porque as referências mudam e, se compararmos a distância euclidiana com a da geometria do táxi sempre podemos afirmar que:
- “A distância Euclidiana, em que podemos andar na diagonal, é sempre menor ou igual à distância calculada pela Geometria do Táxi.”
Raio X
Ofereça a situação que consta no plano original, com a ressalva de fazerem um esboço de um plano cartesiano para resolverem:
“Qual é a menor distância, calculada pela Geometria do Táxi, entre os pontos A e B, em centímetros, sabendo que suas coordenadas são A = (2,3) e B = (-2,-2)? Represente em um plano cartesiano, dois caminhos possíveis para a solução.”
Convite às famílias
Peça para que seus alunos envolvam seus familiares, próximos neste momento, e relatem suas explorações sobre uma nova ideia de geometria.