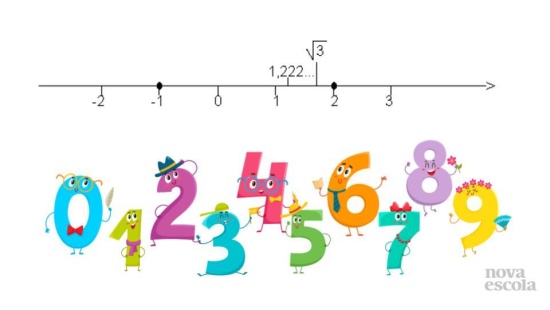
Aquecimento
Plano de Aula
Plano de aula: Diferenças entre números racionais e irracionais
Plano 2 de uma sequência de 10 planos. Veja todos os planos sobre Ampliação dos campos numéricos: números reais
Tem interesse no tema "Neurociência, adolescências e engajamento nos Anos Finais"?
Inscreva-se neste tema para receber novidades pelo site e por email.
Descrição
Este plano de aula foi elaborado pelo Time de autores NOVA ESCOLA
Autora: Maria Bernadete Estradioto
Mentor: Fernando de Mello Trevisani
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNC
EF09MA01; EF09MA02
Ampliação dos campos numéricos: números reais (a necessidade de medir qualquer segmento de reta: números irracionais e seu significado; representação na reta numerada).
Objetivos específicos
Comparar e compreender as diferenças entre os números racionais e os irracionais.
Conceito-chave
Diferença entre os números racionais e irracionais.
Recursos necessários
Projetor ou impressão dos exercícios.
Pré-conhecimento da turma
- Números naturais e números inteiros
- Números racionais e dízima periódica
Habilidades BNCC:
Objetivos de aprendizagem
Comparar e compreender as diferenças entre os números racionais e os irracionais.
Planeje suas aulas pelo Whatsapp!
Qualidade com economia de tempo
Aula
Diferenças entre números racionais e irracionais
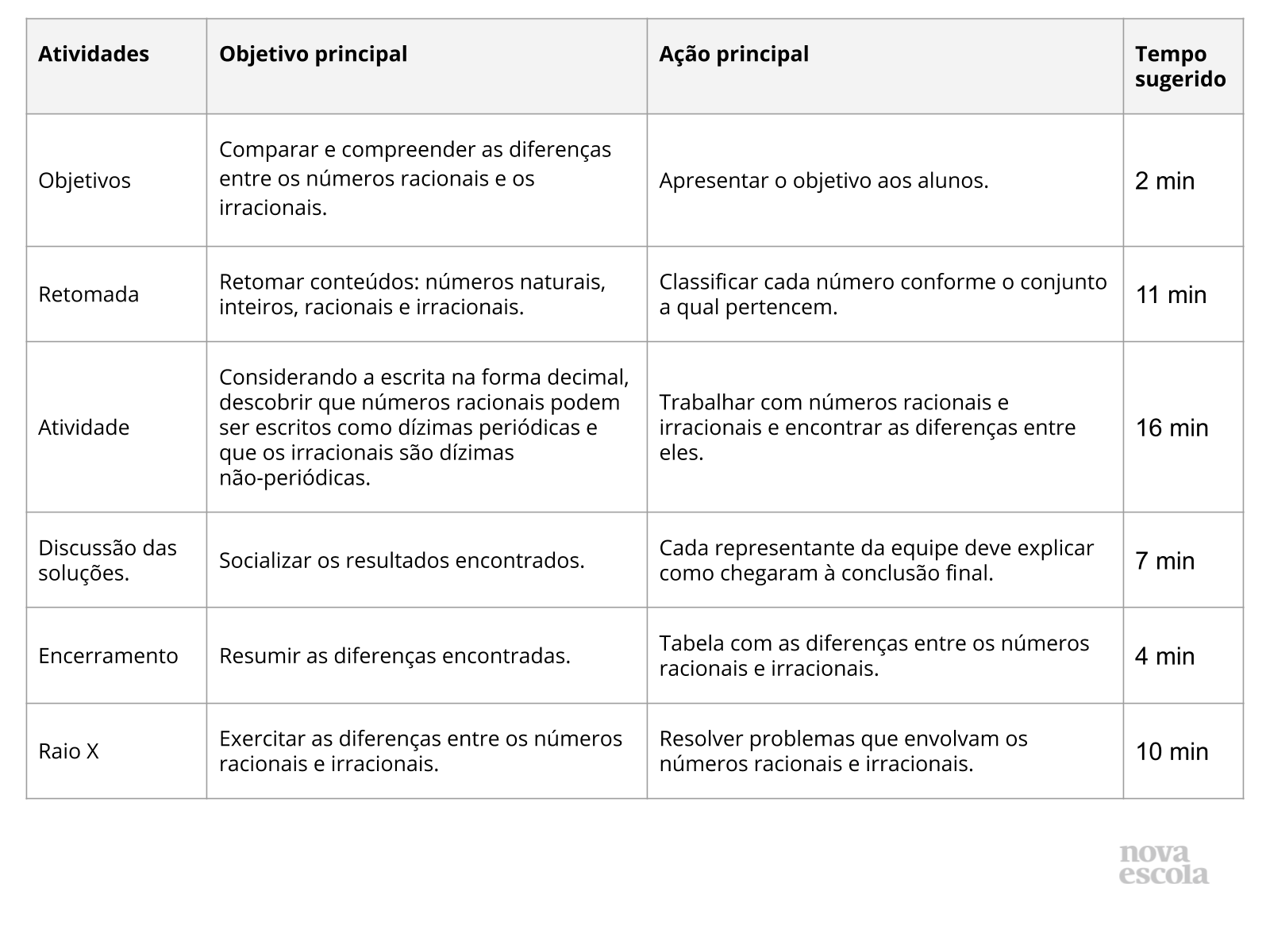
Resumo da aula: A proposta é que, através de uma atividade em grupo, os alunos descubram que existem números decimais infinitos e sem periodicidade, os números irracionais. Para esta aula é importante os alunos saberem calcular a área de um quadrado e extração de raiz quadrada.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado aos alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos
Orientação: o objetivo é retomar os números racionais para em seguida fazer as comparações entre os racionais e irracionais através de perguntas e respostas, e assim os alunos estarem prontos para distinguir um do outro.
Propósito: apresentar o objetivo da aula aos alunos.
Discuta com a turma:
- O objetivo da aula.
Novo curso gratuito

Conheça nosso mais novo curso sobre adolescências, neurociência e engajamento nos anos finais
VER CURSO