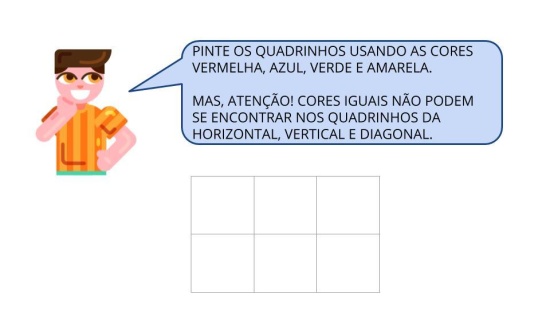
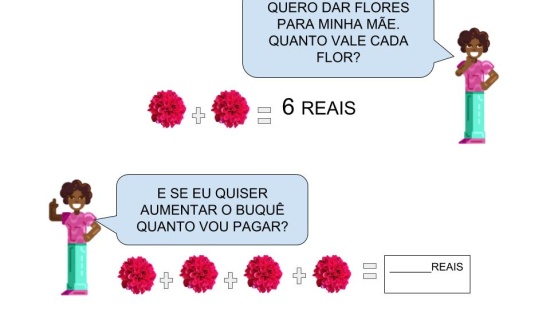
Atividade principal
Plano de Aula
Plano de aula: Poemas ou problemas?
Plano 1 de uma sequência de 10 planos. Veja todos os planos sobre Estratégias de resolução de problemas
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Janaina Pinheiro Vece
Mentor: Mara Elizabeth Mansani
Especialista de área: Rita Batista
Objetivos específicos
Desenvolver estratégias de resolução para o mesmo problema representando-as a partir de diferentes linguagens (desenho, esquema, escrita com palavras ou escritas numéricas)
Conceito-chave
Estratégias de resolução de problema.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não.
Habilidades BNCC:

Precisa de ajuda para criar uma aula personalizada?
Crie seu plano de aula em menos de um minuto no WhatsApp.
Um novo aliado para Professores Alfabetizadores

Acompanhe o progresso dos alunos durante o ano e otimize seu planejamento
ACESSAR AGORA