Atividade principal
Plano de Aula
Plano de aula: Divisão de números inteiros
Plano 4 de uma sequência de 10 planos. Veja todos os planos sobre Operações com números inteiros
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Danilo Pires de Azevedo
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
(EF07MA04) Resolver e elaborar problemas que envolvam operações com números inteiros.
Objetivos específicos
- Realizar divisões envolvendo números inteiros.
- Resolver problemas envolvendo divisões de números inteiros por meio de estratégias pessoais.
Conceito-chave
Divisões de números inteiros
Recursos necessários
Lápis, borracha e caderno.
Habilidades BNCC:
Objetivos de aprendizagem
- Realizar divisões envolvendo números inteiros.
- Resolver problemas envolvendo divisões de números inteiros por meio de estratégias pessoais.
Resumo da aula
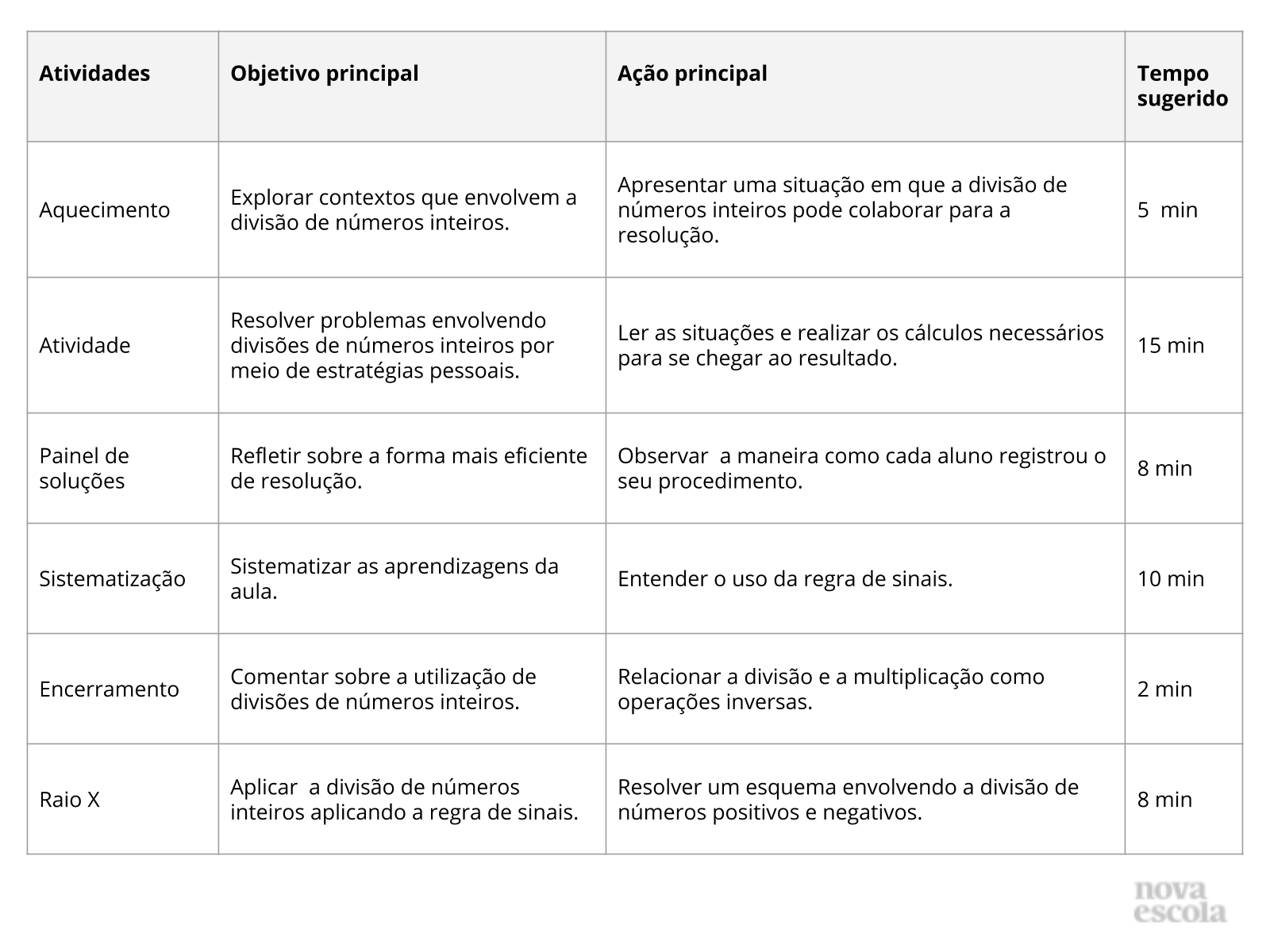 Anotações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Anotações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientações: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento

Tempo sugerido: 5 minutos. (Slides 3 e 4)
Orientações:
- Relembre com os alunos o conceito de operação inversa e faça comentários a respeito de cada uma delas, inclusive as que já foram vistas anteriormente (adição, subtração e multiplicação). Isso facilitará para que relembrem que na adição e subtração não há regra de sinais, porém, na multiplicação, sim.
- Ao trazer a relação entre as operações de divisão e multiplicação, espera-se que os alunos relembrem as relações entre múltiplos e divisores de um número, discutidas no 6º ano do ensino fundamental, conhecido popularmente como “prova real”.
Propósito: Propor que os alunos entendam as operações inversas e as suas relações, com exemplos simples envolvendo números naturais, para posteriormente, envolver os inteiros.
Discuta com a turma:
- Em quais contextos uma divisão de números inteiros pode aparecer?
- É importante conhecer as palavras fator, produto, quociente, dividendo, divisor, entre outras?
- Pensar em uma multiplicação pode auxiliar na resolução da divisão? E as regras de multiplicação de sinais podem ajudar?
Materiais complementares:
A compreensão dos conceitos da “Regra de Sinais” no Ensino Fundamental.
Aquecimento

Tempo sugerido: 5 minutos. (Slides 3 e 4)
Orientações:
Como os alunos já conhecem a regra de sinais, sistematizá-la desde o início ajudará no andamento da aula. Aliás, pode ser de fundamental importância para que os alunos comecem a se familiarizar com essa representação. Evite frases como “Mais com menos dá menos”, “Menos com menos dá mais”, etc. Isso confunde os alunos em diversas situações que envolvem expressões numéricas com números negativos, em que muitos colocam erroneamente “-2-2=+4”, pois “menos com menos dá mais” em uma confusão de regras.
Propósito: Retomar a regra de sinais da multiplicação. Ela também será utilizada na divisão, mas será destacada apenas na sistematização.
Atividade principal
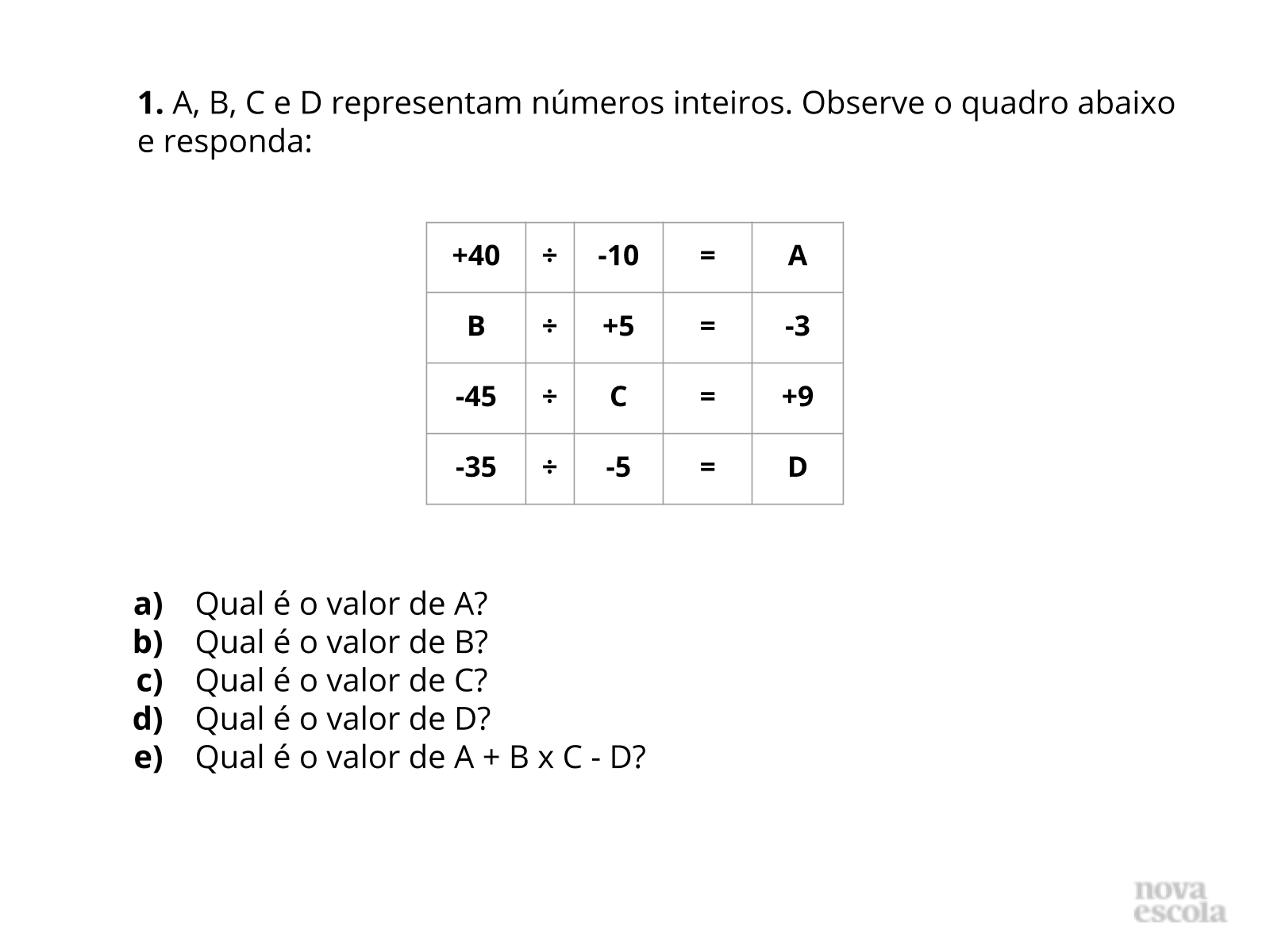
Tempo sugerido: 15 minutos (slides 5 e 6)
Orientações:
- Você pode projetar, imprimir ou anotar no quadro. Agrupe os alunos em duplas ou trios para que compartilhem estratégias para se encontrar os valores desconhecidos. Os alunos podem utilizar diferentes estratégias para determinar os valores desconhecidos. Ainda não comente sobre a regra de sinais da divisão. Deixe que os alunos cheguem à regra fazendo as operações de multiplicação.
- Nos itens a), b), c) e d) os alunos deverão pensar na operação inversa (multiplicação), mas deverão também atentar-se quanto aos sinais das multiplicações envolvidas.
- No item e) os alunos deverão relembrar como resolver uma expressão numérica. Nesse caso, resolve-se primeiro a multiplicação e em seguida efetua-se a adição ou a subtração, o que aparecer primeiro.
- Quando são apresentados os conceitos de múltiplos e divisores, são apresentados somente números naturais. No discuta com a turma, há alguns questionamentos que levarão os alunos a refletir a respeito de divisores (e múltiplos) de números negativos, ou divisores (e múltiplos) negativos de um número inteiro. Afinal, 10 é divisor de 40, mas -10 também o é. Auxilie-os nesta descoberta.
Propósito: Além de propor as divisões, os alunos necessitam relembrar as operações inversas e como são realizadas adições, subtrações e multiplicações com números inteiros, sistematizando e relembrando conteúdos anteriores.
Discuta com a turma:
- A é um divisor de 40?
- B é um múltiplo de 5? E de 3?
- C é um divisor de -45?
- D é divisor de -35?
Material complementar:
Resolução do atividade principal
Leitura sugerida - Aprendizado do trabalho em grupo: aqui.
Atividade principal

Tempo sugerido: 15 minutos (slides 5 e 6)
Orientações: Os alunos deverão preencher as lacunas indicando o quociente na primeira lacuna de cada item e justificando com uma multiplicação, o porquê deste número ser o resultado. Assim, a operação inversa é utilizada e os alunos conseguem compreender melhor qual a relação entre elas.
Propósito: Realizar divisões e multiplicações envolvendo números inteiros, propondo que a regra de sinais seja utilizada adequadamente, relacionando a divisão e a multiplicação.
Discuta com a turma
- Você percebeu o quanto saber multiplicar é importante ao se efetuar a operação de divisão?
Material complementar:
Resolução do atividade principal
Leitura sugerida - Aprendizado do trabalho em grupo: aqui.
Sistematização

Tempo sugerido: 8 minutos (Slides 7 a 9)
Orientações:
- Estimule para que resolvam a divisão da forma como preferirem (mentalmente ou com o uso de algum algoritmo). Utilizar a operação inversa (multiplicação) pode facilitar o raciocínio. Faça algumas perguntas aos alunos caso eles não consigam chegar ao resultado.
- Comente com os alunos sobre a relação da multiplicação e divisão de números inteiros. Retome a regra de sinais e tente criar com os alunos os casos diferentes que aparecem na divisão de números inteiros.
- Caso os alunos tenham dificuldades no sinal do quociente, podem utilizar a multiplicação, para depois, pensar no sinal. Para justificar a escolha, uma multiplicação é utilizada para “provar” que o número é o resultado correto.
- Retome a regra de sinais da multiplicação e em seguida apresente a da divisão entre dois inteiros. Os alunos provavelmente já terão percebido que elas são iguais, alterando apenas o sinal da operação.
- A frase, ao final, retoma uma ideia que pode ser explorada de uma maneira diferentes da que foi proposta, utilizando outras palavras. Evite frases como “Mais com menos dá menos”, “Menos com menos dá mais”, etc. Isso confunde os alunos em diversas situações que envolvem expressões numéricas com números negativos, em que muitos colocam erroneamente “-2-2=+4”, pois “menos com menos dá mais” em uma confusão de regras.
Propósito: Perceber como os alunos compreenderam os conteúdos que foram desenvolvidos.
Discuta com a turma:
- É importante conhecer a divisão e multiplicação entre os números naturais, para se compreender estas operações entre números inteiros?
- O que aconteceu com a regra de sinais para a multiplicação de dois números inteiros?
Sistematização

Tempo sugerido: 8 minutos (Slides 14 a 16)
Orientações: Aqui aparecem os casos de divisão entre números inteiros. Retome cada caso com os alunos e discuta o porquê dos resultados serem positivos ou negativos.
Propósito: Espera-se que os alunos concluam que a regra de sinais é a mesma para a multiplicação e divisão de números inteiros. Essa relação auxiliará muito os alunos em questões futuras, onde essas operações aparecerão em diferentes situações.
Sistematização
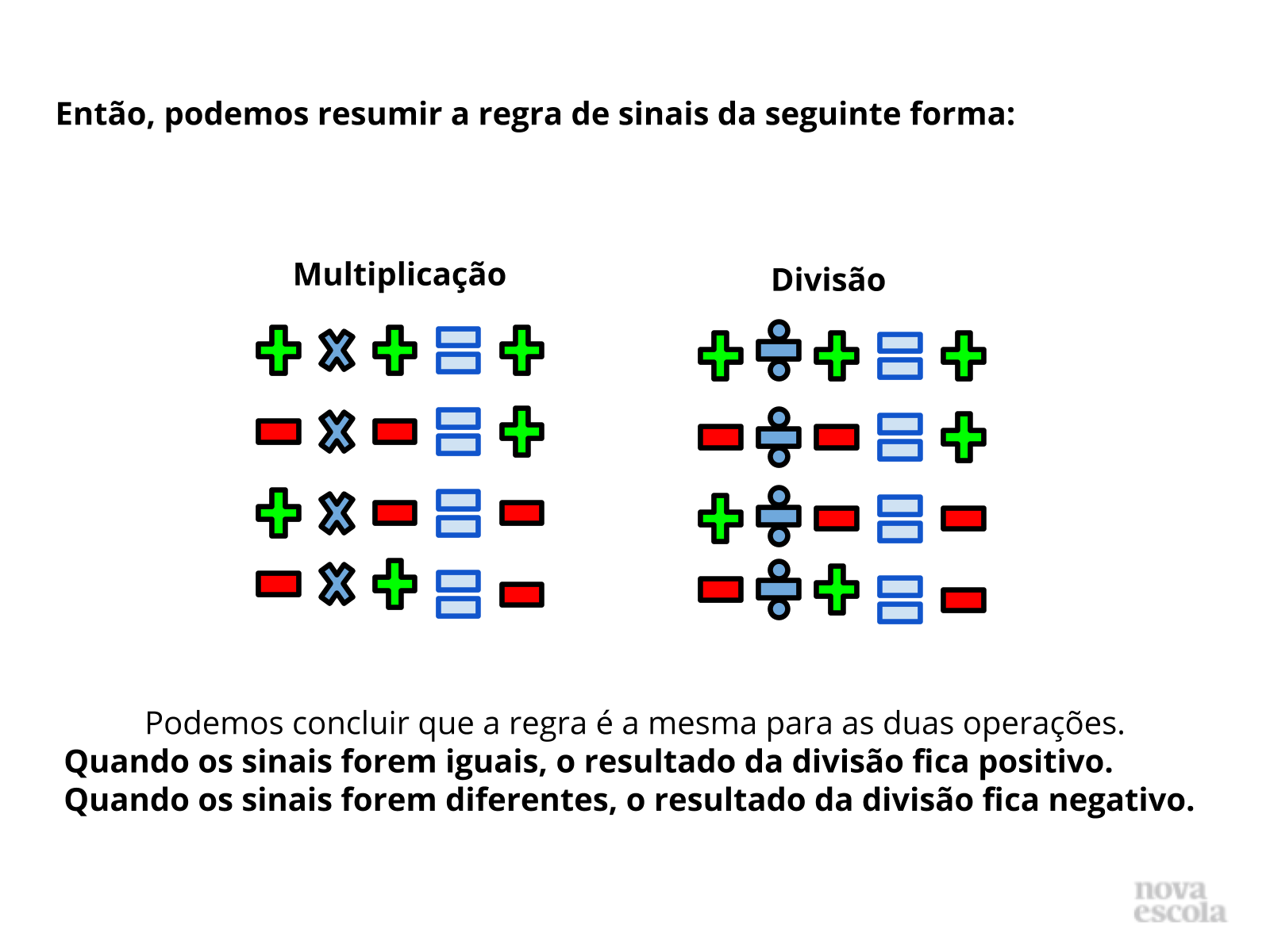
Tempo sugerido: 8 minutos (Slides 14 a 16)
Orientações:
- Retome a regra de sinais da multiplicação e em seguida apresente a da divisão entre dois inteiros. Os alunos provavelmente já terão percebido que elas são iguais, alterando apenas o sinal da operação.
- A frase, ao final, retoma uma ideia que pode ser explorada de uma maneira diferentes da que foi proposta, utilizando outras palavras. Evite frases como “Mais com menos dá menos”, “Menos com menos dá mais”, etc. Isso confunde os alunos em diversas situações que envolvem expressões numéricas com números negativos, em que muitos colocam erroneamente “-2-2=+4”, pois “menos com menos dá mais” em uma confusão de regras.
Propósito: Visualizar a regra de sinais e relacionar as regras da multiplicação com as regras da divisão.
Encerramento

Tempo sugerido: 2 minutos
Orientações: Encerre a atividade retomando com os estudantes a divisão de números inteiros e a regra de sinais. Lembre-se de destacar que essa regra é válida somente para a multiplicação e divisão. Para a adição e subtração é necessário identificar qual é o contexto de cada situação. Isso será discutido nas atividades que envolvem expressões numéricas.
Propósito: Retomar conceitos matemáticos vistos durante a aula, destacando os principais.
Raio-x
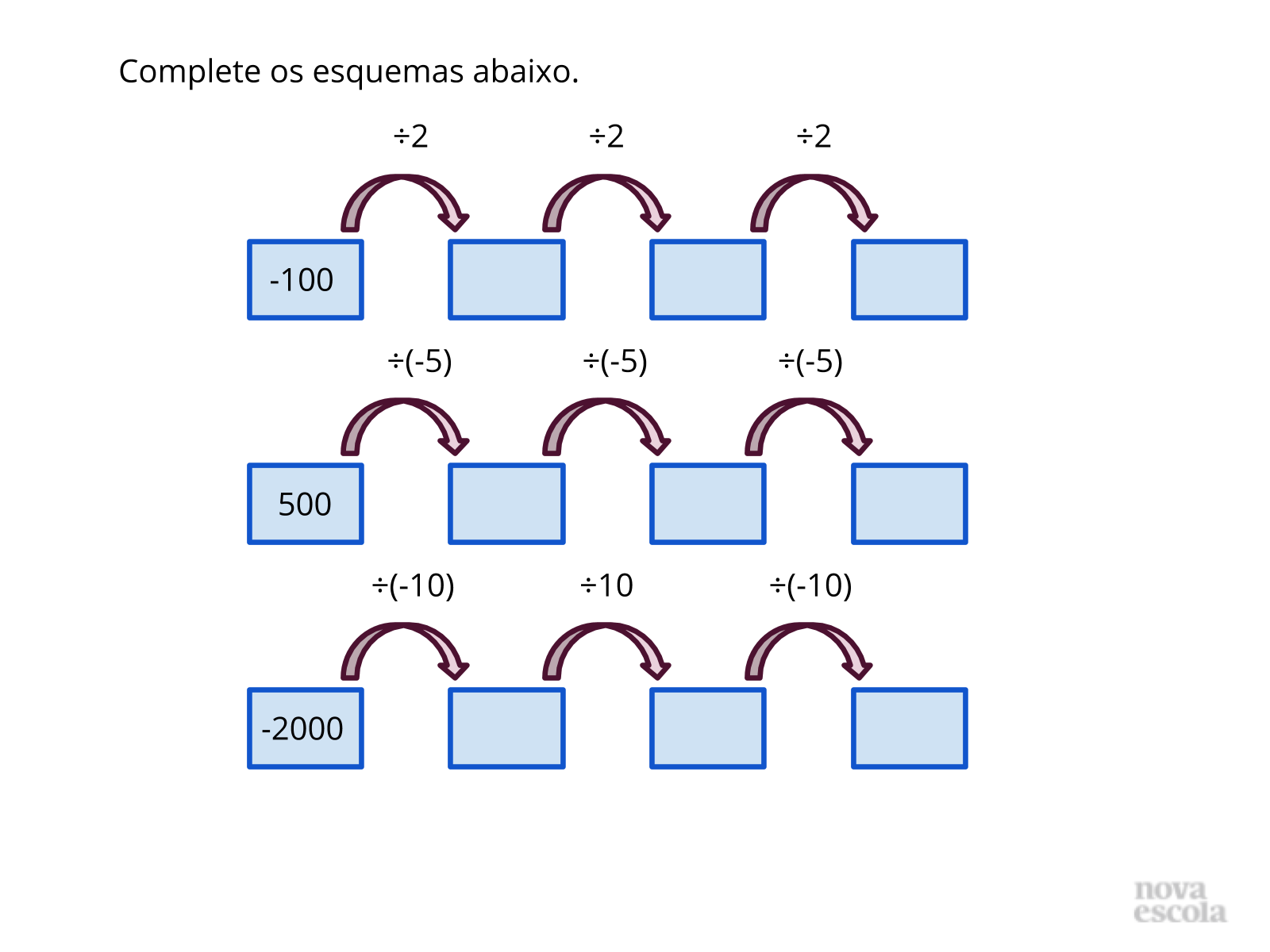
Tempo sugerido: 8 minutos
Orientações:
- Inicialmente não explique como o esquema deve ser completado. Os alunos precisam entender que o primeiro número de cada sequência deve ser multiplicado ou dividido pelo número que aparece sobre a seta.
- Utilize um exemplo com números naturais. É importante que nessa atividade os alunos consigam multiplicar e dividir utilizando números inteiros, aplicando corretamente a regra de sinais até se chegar ao resultado final.
Propósito: Avaliar se os alunos de fato compreenderam os procedimentos envolvidos na divisão entre números inteiros.
Materiais complementares:
Para os alunos
Para o professor
Sugestão de adaptação para ensino remoto
Recursos
Necessários:
- Caderno;
- Lápis;
- Régua;
- Grupo de alunos no Whatsapp.
Opcionais:
- Google Sala de Aula;
- Meet;
- Zoom;
- Atividade online: “Sinais das expressões” - Khan Academy (disponível aqui).
Para este plano, foque na etapa Atividade Principal.
Aquecimento
A atividade é uma retomada de conceitos que são fundamentais para a aula. Organize um encontro usando o Meet ou Zoom para a conversar com os alunos sobre as regras de sinais. Como os alunos já as conhecem, sistematizá-las desde o início ajudará no andamento da aula. Aliás, pode ser de fundamental importância para que eles comecem a se familiarizar com essa representação.
Evite frases como “mais com menos dá menos”, “menos com menos dá mais” etc. Isso confunde os alunos em diversas situações que envolvem expressões numéricas com números negativos, em que muitos colocam erroneamente “-2-2=+4”, pois “menos com menos dá mais” em uma confusão de regras.
Atividade principal
Para a realização da atividade principal, os alunos precisam ter acesso ao problema proposto. Para isso, tire uma foto da atividade principal e disponibilize no grupo de Whatsapp ou Google Classroom, para que os alunos possam pensar sobre e compartilhar estratégias para encontrar os valores desconhecidos.
Oriente-os a filmar ou fotografar as estratégias e respostas, para compartilhar com o professor e a turma no momento da discussão das soluções.
Discussão das soluções
A discussão das soluções da atividade é uma etapa importantíssima da aula. É o momento de justificar as estratégias e respostas usadas para a resolução do problema proposto na atividade principal. Os alunos devem postar os vídeos ou fotografias para compartilhar as respostas em um ambiente de interação, como Whatsapp ou Google Sala de Aula.
A intenção é formar um painel de soluções e promover uma discussão rica e estimuladora entre alunos e professor. Neste momento, estimule a turma a falar (usando a ferramenta de áudio ou vídeo) como pensou para resolver o problema.
Encerramento
Encerre a atividade retomando com os estudantes a divisão de números inteiros e a regra de sinais. Lembre-se de destacar que essa regra é válida somente para a multiplicação e divisão.
Para a adição e subtração, é necessário identificar qual é o contexto de cada situação. Isso será discutido nas atividades que envolvem expressões numéricas.
Proponha que os alunos resolvam a atividade online “Sinais das expressões”, disponível no Khan Academy para fechar o assunto da aula ou colher evidências para uma avaliação.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa. Portanto, indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Danilo Pires de Azevedo
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
(EF07MA04) Resolver e elaborar problemas que envolvam operações com números inteiros.
Objetivos específicos
- Realizar divisões envolvendo números inteiros.
- Resolver problemas envolvendo divisões de números inteiros por meio de estratégias pessoais.
Conceito-chave
Divisões de números inteiros
Recursos necessários
Lápis, borracha e caderno.














