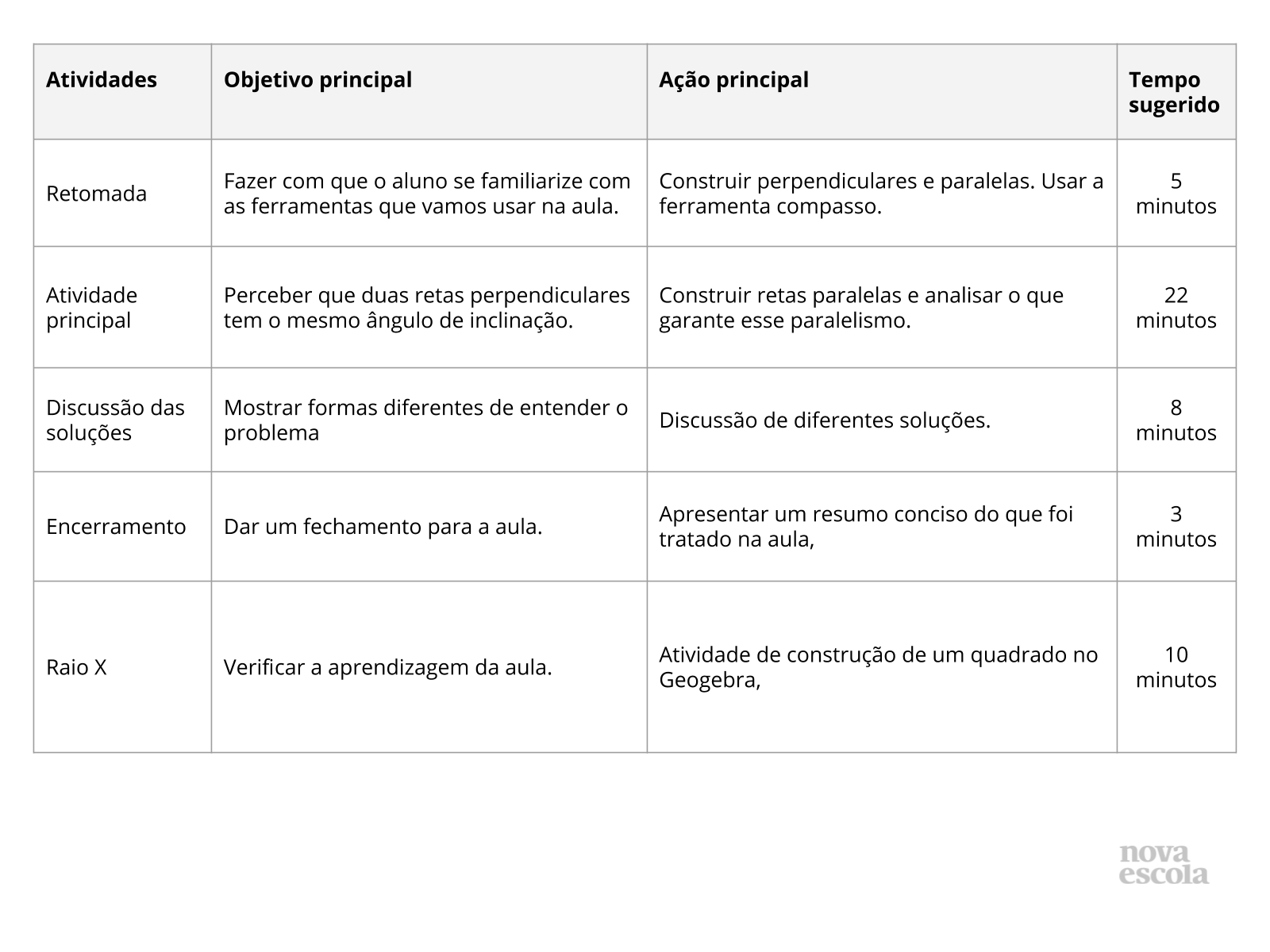
Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos
Orientação:
Leia para o aluno o objetivo da aula. Pode-se apresentar o slide, escrever na lousa ou simplesmente ler.
Propósito:
Deixar o aluno ciente do conteúdo a ser tratado na aula.
Familiarização

Tempo sugerido: 5 minutos.
Orientação:
Diga aos alunos para localizarem no Geogebra as ferramentas Reta, Reta perpendicular, Reta paralela (Você pode orientá-los nessa etapa). Peça aos alunos que construam:
- Duas retas com inclinações diferentes.
- Uma reta paralela para cada reta inicial
- Uma reta perpendicular para cada reta inicial.
A cada passo discuta sobre a montagem de cada objeto. Por exemplo, para construir uma reta paralela a outra reta eu tenho que primeiro fazer um ponto pelo qual quero traçar a paralela e depois clicar na reta original. Pergunte ao aluno, por exemplo, “Como eu começo a traçar essa reta?”; “O que eu preciso fazer primeiro?”. As primeiras retas (que os alunos traçaram) provavelmente não serão perpendiculares nem paralelas, então é interessante introduzir o conceito de retas concorrentes. Primeiro pergunte para a turma se alguém sabe qual é o nome. Caso contrário, explique. Não precisa elaborar muito. “Essas retas se cruzam, mas não são perpendiculares. Quando duas retas se cruzam elas são concorrentes. Podem ser concorrentes e perpendiculares (porque as perpendiculares se cruzam) ou só concorrentes, como essas que vocês fizeram.”.
Quando a montagem estiver clara, peça que selecionem todos os objetos (Editar - Selecionar tudo) e apaguem tudo (Apagar) para fazer a próxima atividade.
Propósito:
Fazer com que os alunos se familiarizem com as ferramentas que vão utilizar para que possam se concentrar na atividade em si.
Discuta com a turma:
- O que é necessário para montar uma reta?
- O que é necessário para montar uma reta paralela? E uma perpendicular?
- Eu posso começar uma atividade fazendo uma reta paralela? E uma perpendicular?
- O que é necessário para construir uma circunferência com o compasso?
- Pra que serve o segmento que eu faço antes de fazer a circunferência?
Materiais complementares para impressão:
Aquecimento
Resolução do Aquecimento
Materiais Complementares:
Manual Geogebra 5.0 (português) - https://wiki.geogebra.org/pt/Manual (visitado em 09/12/2017).
Software Geogebra online: https://www.geogebra.org/classic (visitado em 09/12/2017).
Ogeogebra - site com dicas e vídeos - http://ogeogebra.com.br/site/ (visitado em 09/12/2017).
Construções

Tempo sugerido: 22 minutos
Orientação: Diga aos alunos que eles irão construir uma reta perpendicular a outra, sem usar a ferramenta Reta perpendicular. Você vai orientá-los na construção da reta perpendicular e da reta paralela, sem o uso das ferramentas prontas. Após fazer as duas retas paralelas, pergunte a eles quais foram as etapas da construção. Ao final pergunte como foi feita a construção (não queremos saber detalhes do tipo: “com a ferramenta Compasso…”, queremos saber apenas a sequência de retas como: construímos uma reta inicial depois construímos uma reta perpendicular a esta e, por último, construímos uma reta perpendicular à última). Depois que eles perceberem essa ordem, pergunte: “Como eu sei que estas retas são paralelas?”.
Obs: A orientação para as construções está na Resolução da Atividade Principal.
Propósito: Fazer com que os alunos percebam a relação entre paralelas e perpendiculares.
Discuta com os alunos:
- Eu quero fazer uma perpendicular, como eu começo?
- Como eu sei que as retas que eu construí são paralelas mesmo?
Materiais complementares para impressão:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Discutindo soluções

Tempo sugerido: 8 minutos
Orientação:
No slide há algumas soluções possíveis, mas o ideal é usar as soluções, os erros e as dificuldades dos próprios alunos, se possível apresentadas por eles mesmos. Apresente ou peça que os alunos apresentem na frente suas soluções. Procure soluções diferentes que estejam corretas e incorretas. Pergunte aos alunos a forma como eles pensaram para chegar àquela resolução. Nos exemplos o balão verde fala que as retas são paralelas ou perpendiculares. Isso está incorreto porque elas podem ser concorrentes sem serem perpendiculares ou podem ser reversas (estão em planos diferentes com direções diferentes). No balão rosa, a menina diz que todas as retas que são perpendiculares à outra perpendicular são paralelas. Não está totalmente incorreto, então, primeiro peça que ela dê exemplos diferentes (apenas mudando a altura da perpendicular já temos uma outra reta paralela). Feito isso, fale para eles sobre as retas reversas. “Só que pode acontecer outra coisa também. Eu vou pegar essas duas canetas representando duas retas perpendiculares. Se eu fizer uma outra perpendicular assim (no mesmo plano), aí você está certa. Essa outra caneta é paralela à primeira. Mas e se eu fizer uma perpendicular assim (reversa. Basta mudar a direção da perpendicular)”. O garoto do balão amarelo diz que se uma reta é perpendicular duas vezes ela vira paralela. É uma versão menos geral da menina do balão rosa, o problema é que, além da questão da reta reversa, aqui há um problema na descrição da solução. Ele fala em uma reta sendo perpendicular duas vezes ela será paralela, mas ele está falando de três retas e fala como se fosse uma só. A questão aqui é usar as palavras perpendicular e paralela para uma reta só, como se não fosse uma relação. Uma reta não pode ser perpendicular ou paralela simplesmente. Ela tem que ser perpendicular à outra reta e o mesmo vale para as paralelas.
Propósito:
Perceber, através do erro, quais caminhos eu posso tomar para resolver o problema e como chegar a uma resposta que esteja mais próxima de uma explicação matemática.
Discuta com os alunos:
- Por que estas duas retas são paralelas e estas outras não?
- O que faz com que uma reta seja perpendicular à outra?
- Qual a relação entre essas duas retas que são paralelas e essa que é perpendicular à primeira e à segunda?
Encerramento

Tempo sugerido: 3 minutos.
Orientação:
Apresentar o conteúdo da aula de forma concisa.
Propósito:
Dar um fechamento à aula.