Resumo da aula
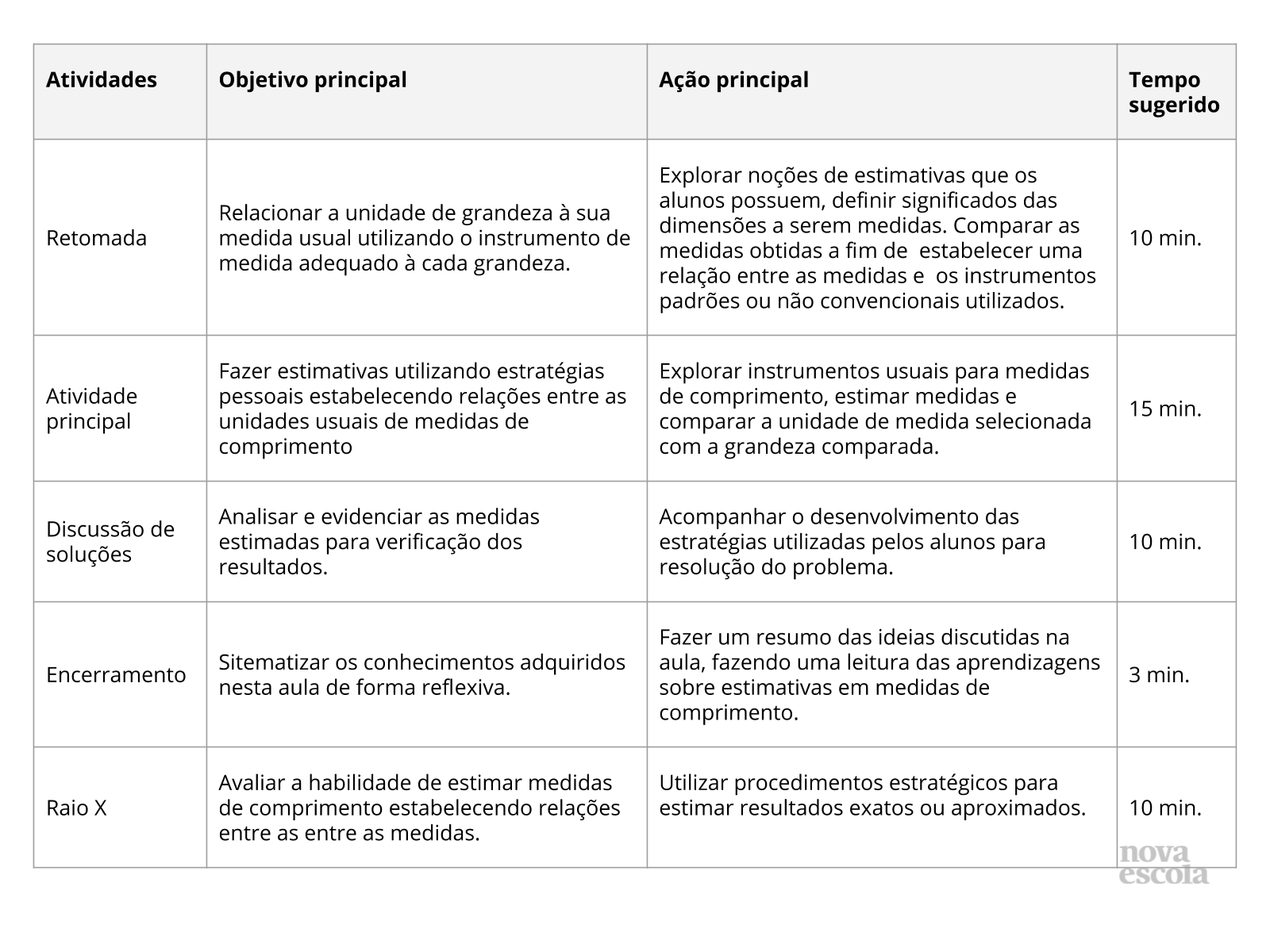
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para turma.
Propósito: Compartilhar com a turma o objetivo da aula.
Retomada

Tempo sugerido: 10 min.
Orientação: Inicie a aula projetando o texto do slide e abordando alguns conceitos como o significado das palavras altura, comprimento, largura, espessura. Esses termos são usados para indicar o que querem medir. Peça aos alunos para que pesquisem no dicionário, com a ajuda do professor, o significado de cada termo.
Agrupe os alunos em duplas e peça que anotem no caderno o quanto eles acham que mede (estimativa) a caneta e o lápis de cada um.
Em seguida, determine um tempo para que comparem suas estimativas. Observe qual a dificuldade em estimar e se os resultados foram diferentes apenas nos tamanhos dos palmos ou se algum aluno não domina os conceitos de estimativas e as equivalências entre as unidades de medidas.
Após essa etapa, questione aos alunos se as estimativas que fizeram podem ser verificadas com uma régua. Disponibilize uma régua para que visualizem. Essas representações mentais facilitam as estimativas. Compare novamente as medidas. Essa atividade fará com que o aluno perceba a equivalência entre as medidas não convencionais e as padronizadas (um palmo mede quantos cm?) ou, até mesmo, entre duas medidas não convencionais (quantos palmos correspondem ao comprimento de uma mesa?)
Enquanto os alunos realizam as medidas, circule pela sala e observe as estratégias pessoais que cada um usou para responder o que foi solicitado.
Propósito:
- Promover a reflexão e levá-los a perceber que quando medimos um comprimento, comparamos esse comprimento a outro comprimento.
- Explorar e conhecer a noção de estimativa que os alunos dominam.
Discuta com a turma:
- As estimativas que vocês fizeram, foram iguais?
- Qual foi a estratégia usada para estimar as medidas solicitadas?
- Por que houve tantas variações entre os resultados estimados?
- A medida obtida pela estimativa foi exata?
- O que significam os risquinhos menores na régua? E os maiores?
- Quantas divisões dos risquinhos maiores tem na régua?
- O que significa cada divisão dessas?
- A medida do objeto que você estimou é maior ou menor que 1 cm?
- É maior ou menor que um mm?
- A medida do seu colega foi parecida com a sua?
- E se eu quiser medir a largura de um caminhão, ou a altura da entrada de um túnel, ou mesmo o comprimento de uma cama? Qual instrumento de medida seria o ideal para medir?
- E se eu quisesse medir o comprimento de uma formiga? E a espessura de uma borracha?
- A medida estimada inicialmente do lápis e da caneta foi aproximada com a medida obtida com a régua?
- Qual foi sua maior dificuldade ao medir os objetos?
Atividade principal
Tempo sugerido: 15 minutos.
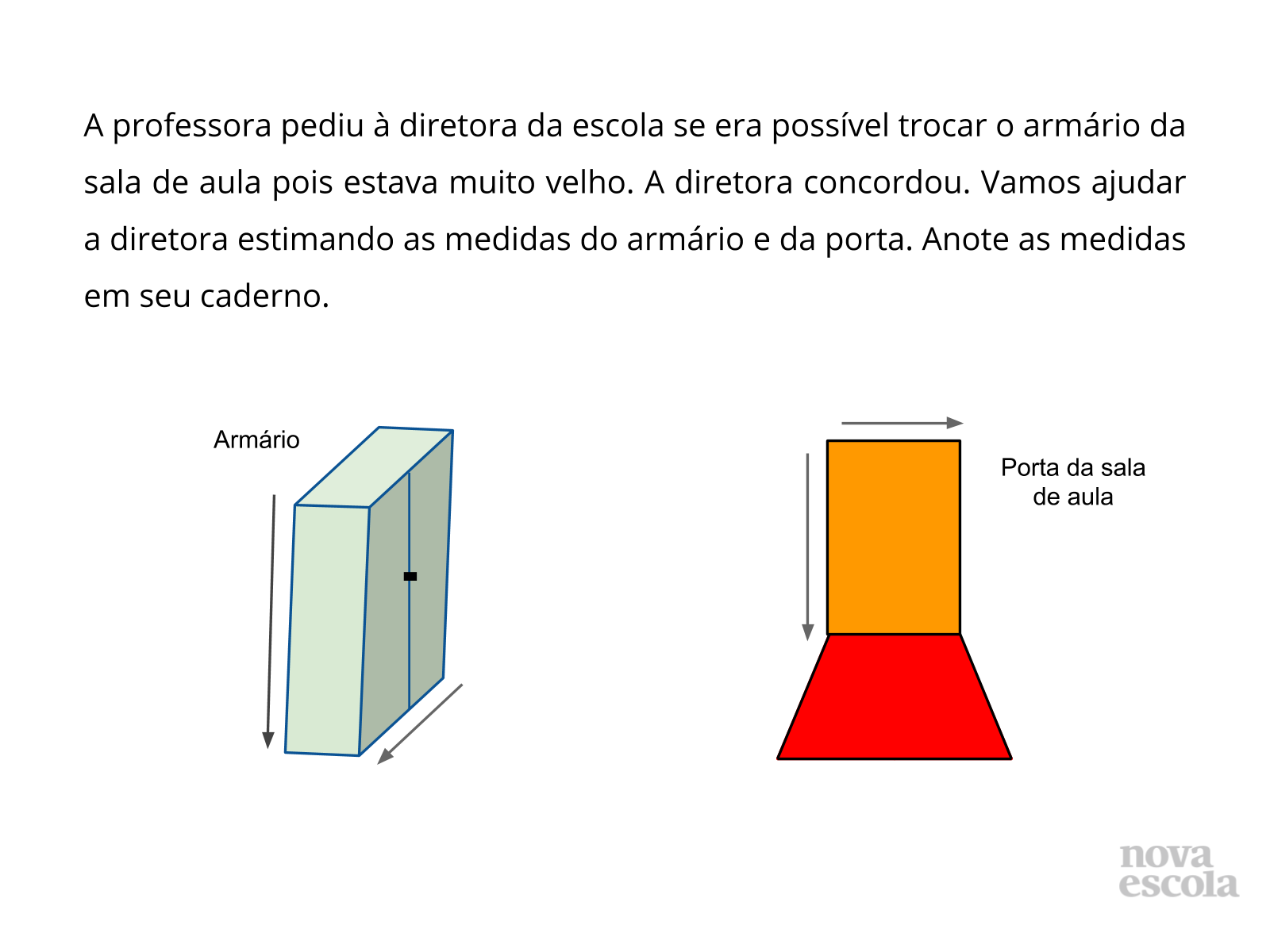
Orientação: Inicialmente peça aos alunos que pesquisem no dicionário o significado dos termos: altura, largura, espessura e comprimento, a fim de distinguir qual é o lado que terão de medir, tendo em vista que o armário tem três dimensões. Em seguida, os alunos poderão discutir uma estratégia para estimar as dimensões sem usar os instrumentos de medidas e de maneira que o resultado seja o mais próximo do exato. Nestas situações, poderão utilizar o palmo, levando em consideração que o objeto a ser medido permite o uso deste recurso. As estimativas podem ser anotadas no caderno para posterior comparação.
Comente com os alunos que os palmos são apenas uma estimativa e que para obtermos a medida exata, faz-se necessária a transformação em uma unidade de medida padronizada. O professor pode sugerir brevemente a transformação de uma medida coletivamente, contornando o palmo de sua mão bem aberta no quadro e, em seguida, fazer o cálculo da transformação.
Divida a sala em grupos, enquanto um grupo fica encarregado de estimar as medidas da porta, outro irá se encarregar das medidas do armário. Fazer dessa forma para que todos tenham oportunidade de estimar as medidas, compará-las e, passar pela verificação. Oriente-os a fazer uma tabela no mesmo modelo que consta no slide 6 para que possam registrar as medidas efetuadas e para posterior análise e comparação.
Enquanto realizam essa tarefa, observe nas duplas as estratégias usadas para medir, se estão medindo os lados que foi solicitado. Após esse tempo, compartilhe com a turma as medidas estimadas, compare-as e questione-os sobre as variações nos resultados obtidos e o motivo de tais variações.
Propósito: Fazer com que os alunos percebam que é possível estimar medidas baseados nas unidades convencionais (palmo), porém, sem obter a medida exata. Explorar estratégias pessoais de medição.
Discuta com a turma:
- De que maneira vocês realizaram a estimativa das medidas?
- As estimativas foram iguais?
- Os resultados foram exatos?
- Por que as estimativas variaram de uma dupla para outra?
- Vocês estimam que a altura da porta é maior ou menor que 1 metro?
- E do armário? É maior ou menor que um metro?
- Qual dimensão é maior, a largura ou a altura dos objetos medidos?
- Qual é a diferença de medida (palmos) entre as duas dimensões?
- O que vocês podem concluir após as comparações feitas entre as várias medidas encontradas?
Materiais complementares
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Discussão da solução

Tempo sugerido: 10 minutos.
Orientação: Depois que os alunos compararam suas estimativas e estratégias de resolução, apresente os slides 5 (reconhecimento do significado dos termos) e 6, para que observem se seus resultados coincidem com os da tabela ou do quadro, dependendo da forma que o professor registrou (os resultados desta tabela são baseados em uma estimativa de quanto mede um palmo de uma criança). Discuta novamente com a turma sobre as variações de medidas encontradas. Discuta quais foram as razões que levaram à padronização das unidades de medidas.
Propósito: Realizar um fechamento das ideias discutidas até o momento.
Discuta com a turma:
- Podemos relacionar uma medida não convencional com outra adotada como convencional?
- Quais razões levaram à padronização das unidades de medidas?
- Qual foi a equivalência que você percebeu entre as medidas?
- Como você explicaria o conceito de medida agora?
- Como você conceituaria o termo “estimar”?
Discussão da solução
Tempo sugerido: 10 minutos.
Orientação: Assim que os alunos concluírem suas estratégias de cálculo e estimativas, socializar as soluções que encontraram, registrando e comparando um resultado ao outro.
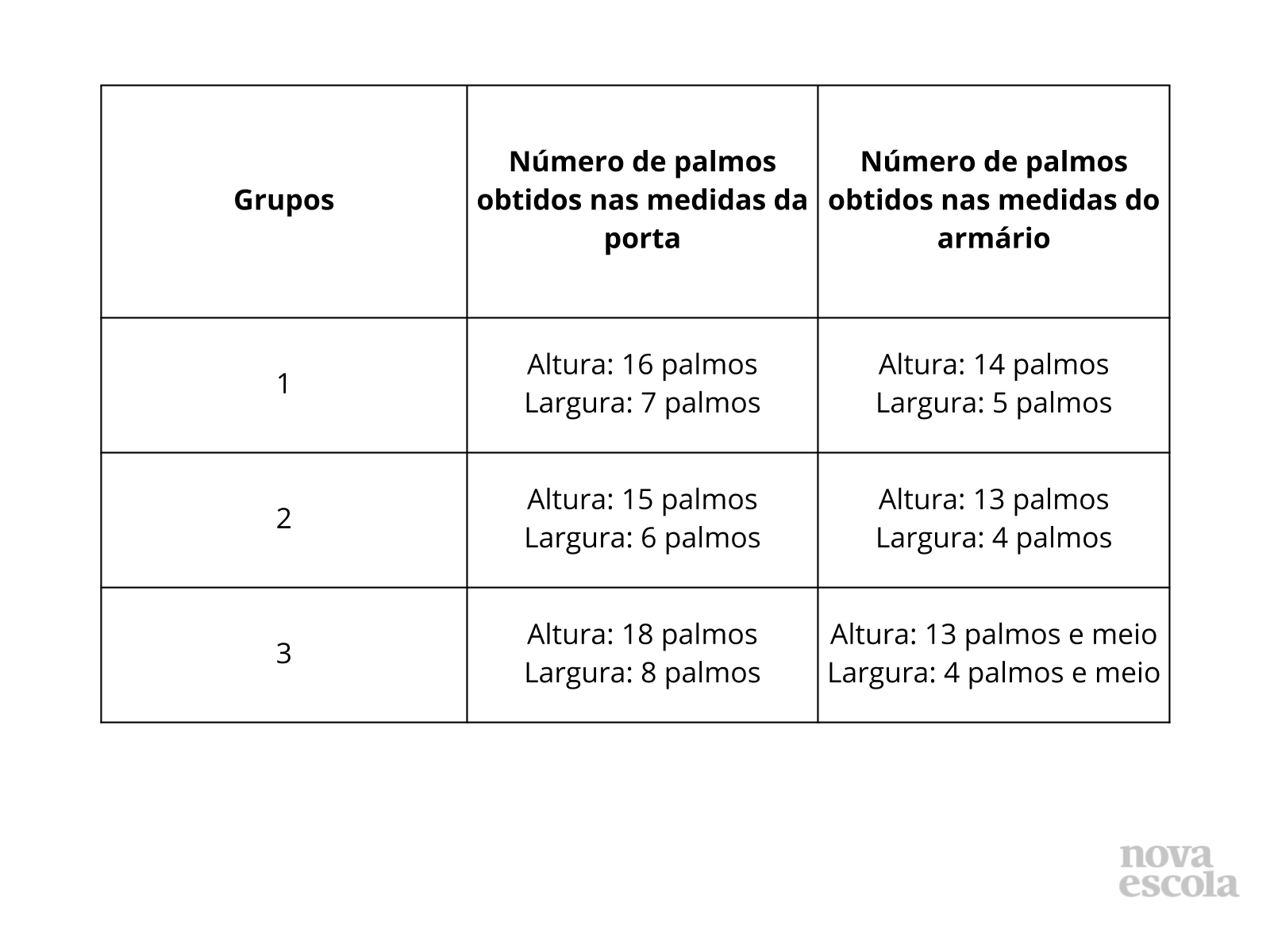
Projete a tabela no multimídia somente quando os alunos concluírem suas estimativas. Caso necessário, o professor pode utilizar o quadro para registrar as estimativas para posterior comparação. A resposta dessa estimativa é aberta pois temos armários e portas de várias medidas.
Compare as estimativas para que os alunos percebam que o número de palmos obtidos para uma mesma medida pode ser diferente, pois nem todos têm o mesmo tamanho de palmo. Através dessa atividade poderão refletir sobre a conservação da proporcionalidade de tamanho e a necessidade de padronização das unidades de medidas.
Propósito: Realizar um fechamento das ideias discutidas até o momento, levando-os a refletirem sobre as estratégias pessoais utilizadas nas resoluções e as diferentes respostas encontradas. Levar os alunos a refletirem que quanto maior o tamanho da unidade, menor é o número de vezes que se utiliza para medir um objeto.
Discuta com a turma:
- Vocês perceberam alguma diferença entre o número de palmos de cada aluno?
- Por que houve essa variação?
- O que vai acontecer se eu usar as medidas do João aos invés de usar as medidas do Kauê para concluir se o armário passa pela porta?
- A partir das medidas obtidas, como faremos para passar o armário pela porta? Será necessário desmontá-lo? (Essas intervenções vão depender do modelo do armário).
- Como podemos fazer em uma situação em que o armário seja mais largo que a porta? ( Essas discussões vão depender do modelo do armário, alguns são mais largos outros mais compridos, nesse caso, os alunos irão encontrar uma estratégia para que consigam passar o armário pela porta).
Encerramento

Tempo sugerido: 3 minutos.
Orientação: Professor, este é o momento de fazer uma revisão geral de tudo o que foi trabalhado nesta aula sobre estimar medidas de comprimento.
Propósito: Fazer um fechamento das ideias exploradas nesta aula, sistematizando as aprendizagens.
Raio X

Tempo sugerido: 10 minutos.
Orientação: Peça que individualmente os alunos leiam a atividade proposta, bem como os cálculos de estimativas das medidas pedidas, utilizando os conhecimentos adquiridos na aula. Sugira que estimem as dimensões da janela, em um primeiro momento, apenas pela observação. Em seguida, utilizar o palmo como medida não padronizada para comparar as estimativas feitas.
Nessa comparação, aproveite o momento para relembrar que quanto maior a unidade usada para medir menor será o número de vezes que se utiliza a grandeza para medir um objeto. Relacionar essa ideia à medida padronizada, o milímetro, parte menor do metro cabem mais vezes dentro dessa unidade do que o centímetro que embora seja menor que um metro é maior que o milímetro.
O Raio X é o momento de avaliar se os alunos conseguiram identificar grandezas mensuráveis que ocorrem no seu dia a dia, convencionais ou não, relacionadas ao comprimento.
Discuta com a turma:
- Qual a estimativa que você pode fazer das dimensões dessa janela apenas pela observação? Quantas vezes seu palmo caberá nessas dimensões?
- O que vocês concluíram após a análise das diferentes estimativas?
Materiais complementares
Raio X
Resolução do Raio X
Atividade complementar
Resolução da Atividade Complementar
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. 























