Atividade principal
Plano de Aula
Plano de aula: Ampliando a Reta Numerada
Plano 4 de uma sequência de 10 planos. Veja todos os planos sobre Números decimais exatos, dízimas periódicas e frações
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Rodrigo Rios Nascimento
Mentor: Amanda Ferreira Verardo Bilia
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
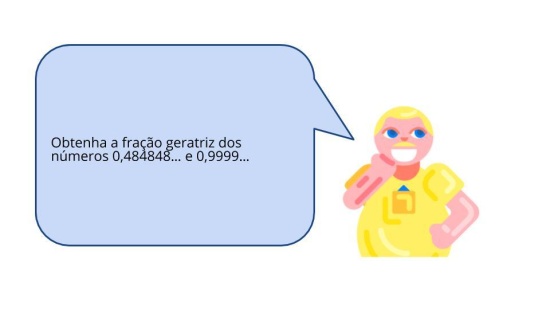
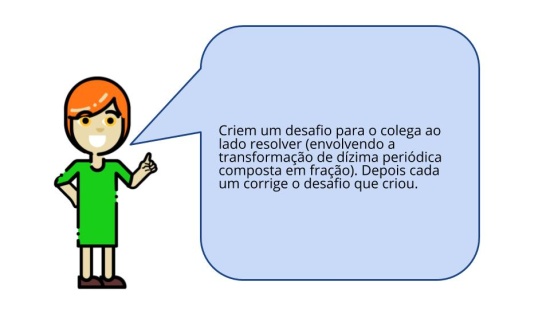
(EF08MA05) Reconhecer e utilizar procedimentos para a obtenção de uma fração geratriz para uma dízima periódica.
Objetivos Específicos
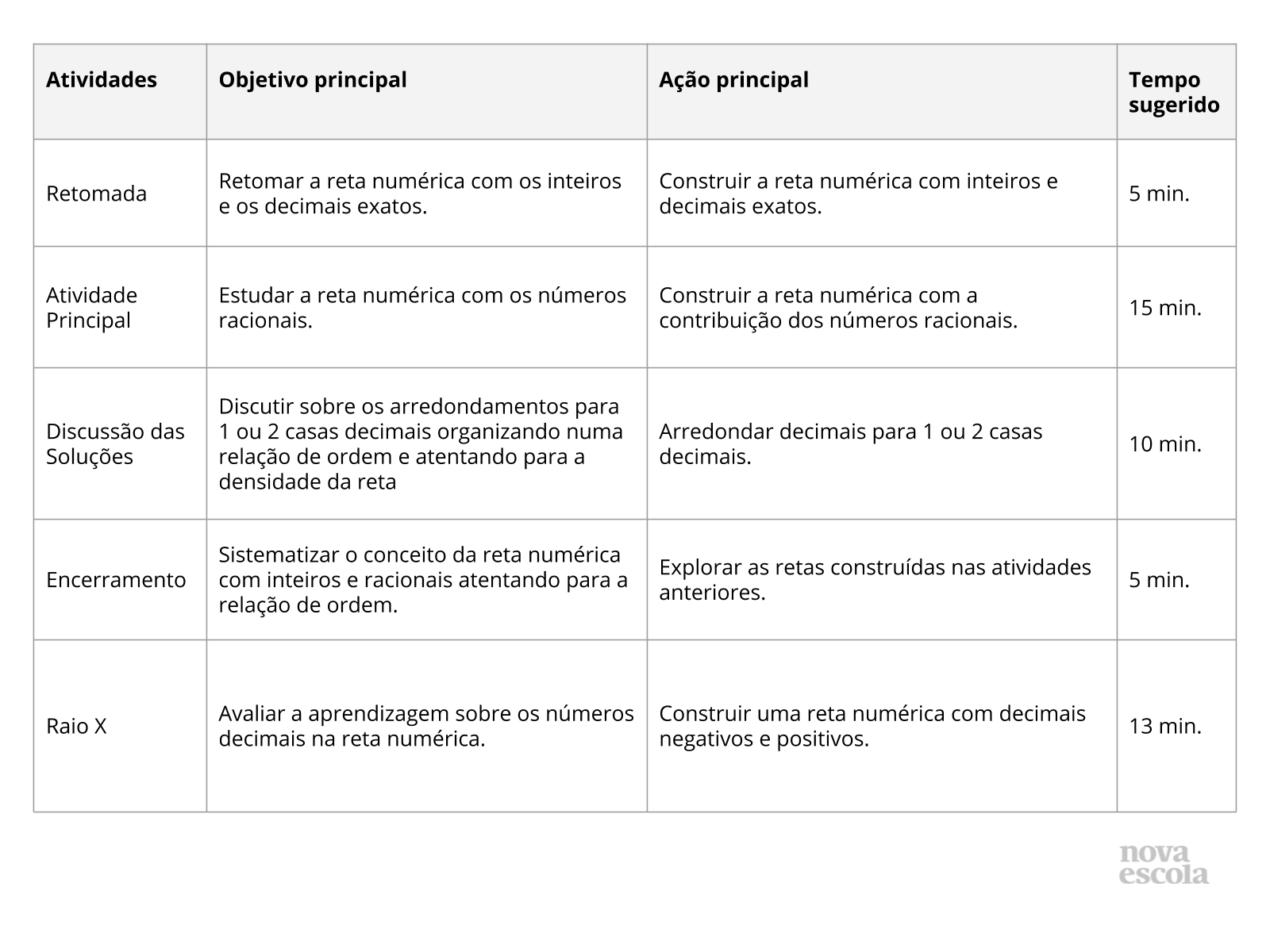
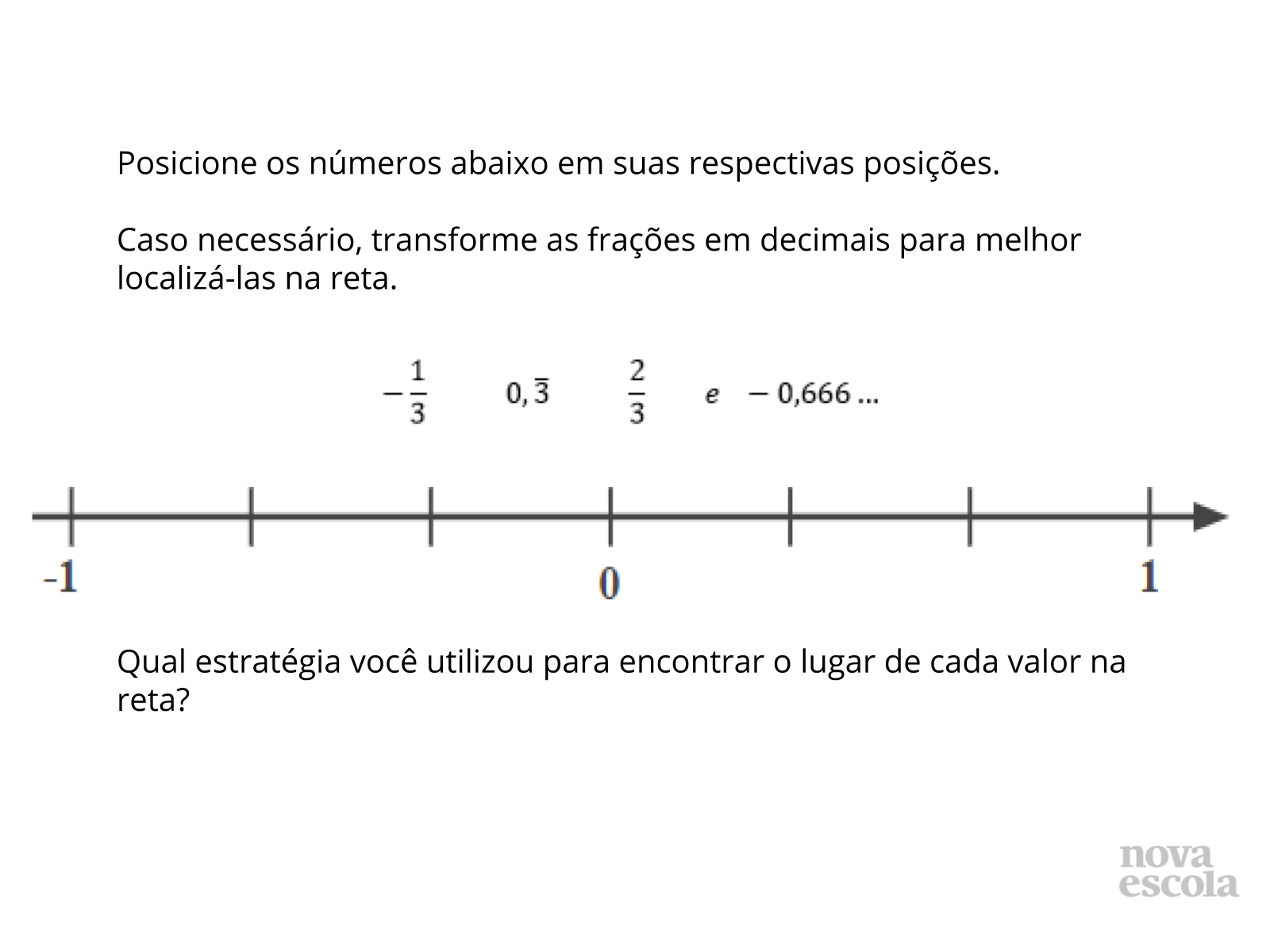
Identificar os números decimais na reta numerada.
Conceito-chave
Reta numerada, números decimais.
Recursos Necessário
- Atividades impressas em folhas, coladas no caderno ou não.
Habilidades BNCC:
Objetivos de aprendizagem
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Rodrigo Rios Nascimento
Mentor: Amanda Ferreira Verardo Bilia
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
(EF08MA05) Reconhecer e utilizar procedimentos para a obtenção de uma fração geratriz para uma dízima periódica.
Objetivos Específicos
Identificar os números decimais na reta numerada.
Conceito-chave
Reta numerada, números decimais.
Recursos Necessário
- Atividades impressas em folhas, coladas no caderno ou não.