Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Descreva para turma o objetivo da aula. É importante ressaltar que o esforço produtivo dos alunos deve ser incentivado a fim de que os mesmos sejam capazes de criar estratégias para interpretar a potência de decimais.
Propósito: Compartilhar com a turma os objetivos da aula, incentivando o processo de autonomia.
Retomada
Tempo sugerido: 5 minutos
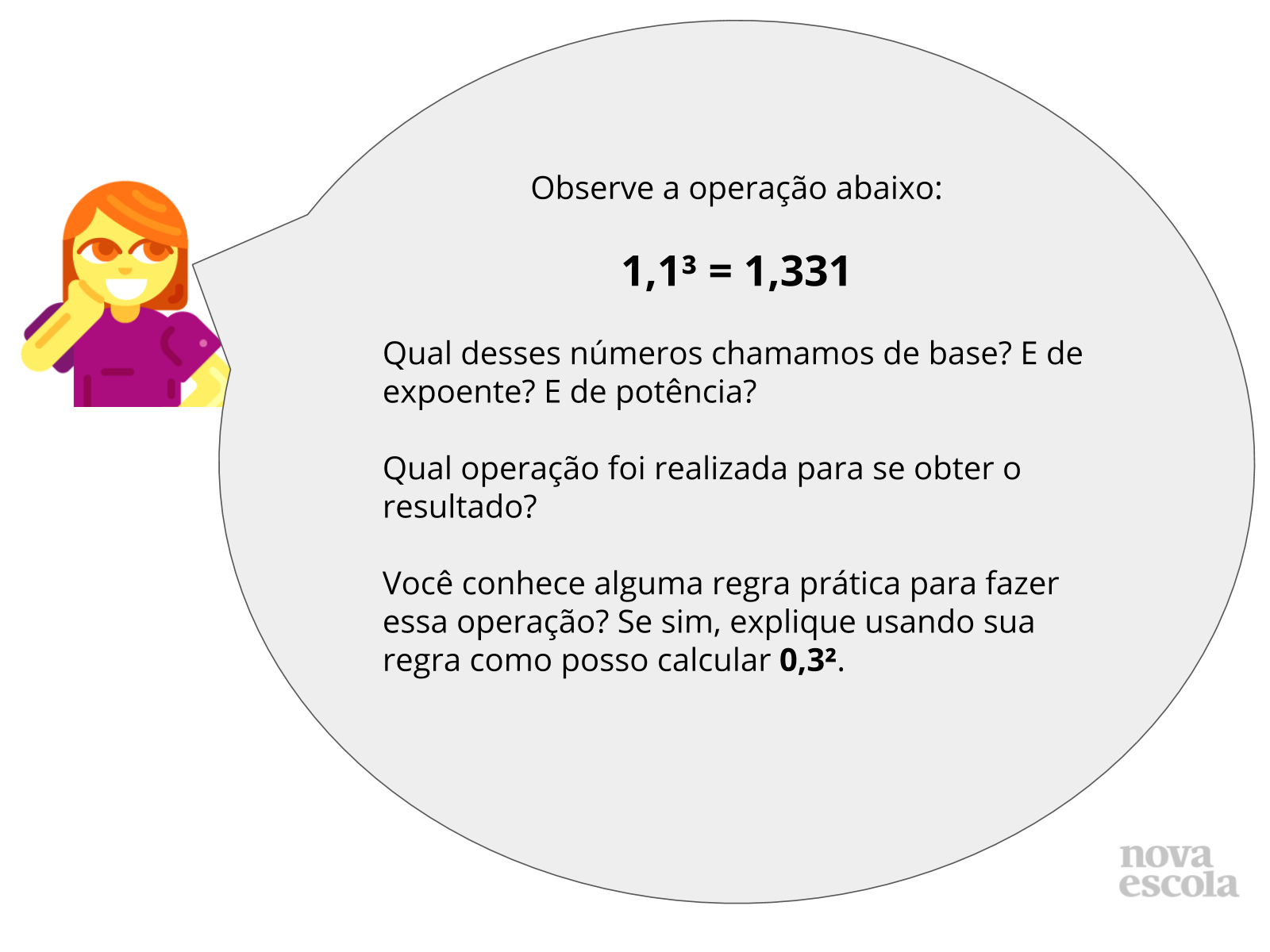
Orientação: Se possível use o projetor ou faça um esboço deste slide, escrevendo as operações na lousa e fazendo as perguntas oralmente. Espera-se que os alunos se lembrem de quais são os nomes de cada termo em uma potenciação e saibam reescrever 1,1³ como 1,1 x 1,1 x 1,1.
Alguns alunos podem se lembrar que esse cálculo pode ser feito resolvendo 11 x 11 x 11 = 1331 e em seguida colocando a vírgula após o primeiro 1 (contando 3 ordens da direita para a esquerda, valor equivalente ao total de casas decimais dos fatores da multiplicação).
Para a última operação, usando essa regra, basta fazer 3 x 3 = 9 e lembrar de contar duas casas para colocar a vírgula, chegando em 0,09.
Propósito: Ambientar a turma para as atividades que virão a seguir.
Discuta com a Turma: Discuta nesta etapa a importância de se saber lidar com cálculos que envolvam potenciação, visto que esse é um conteúdo que os acompanhará por toda trajetória escolar, com aplicações diversas que vão desde de situações que envolvam aplicações financeiras, até desenvolvimentos biológicos ou sociais.
Atividade Principal (Slides 4 e 5)

Tempo sugerido: 25 minutos
Orientação: Se possível, projete os slides para que todos possam acompanhar. Os alunos podem copiar as questões no caderno ou utilizar a atividade impressa (o link está abaixo). Divida a classe em grupos de 3 ou 4 alunos e deixem que eles explorem a atividade. Incentive o uso da calculadora. Se notar que a sala toda está parada no mesmo obstáculo, retome a atenção e faça algumas perguntas motivadoras como as que aparecem no guia de intervenção.
Propósito: O objetivo da atividade é fazer com que o aluno analise o uso da potência de decimal em uma situação prática, construindo significados para seu uso.
Discuta com a turma: Ao decorrer da atividade, faça perguntas à turma a respeito da potenciação e utilize a calculadora para explorar o conteúdo.
- Vocês perceberam alguma ligação entre o número de casas decimais e o expoente envolvido em cada operação?
- E se ao invés do desconto ser de 0,5 elevado ao número de erros fosse 0,15. Quantos pontos perderia Bruno?
- Nessa nova situação você percebe qual a relação entre o número de casas decimais e o expoente?
- O resultado do cálculo de uma potência sempre será um valor maior que a base?
- O que aconteceu quando elevamos 0,5 ao quadrado (expoente 2)? E quando elevamos 0,5 ao cubo (expoente 3)?
- O que acontece com a pontuação caso não ocorram erros ou acertos?
Materiais complementares para impressão:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade Principal (Slides 4 e 5)

Tempo sugerido: 25 minutos
Orientação: Se possível, projete os slides para que todos possam acompanhar. Os alunos podem copiar as questões no caderno ou utilizar a atividade impressa (o link está abaixo). Divida a classe em grupos de 3 ou 4 alunos e deixem que eles explorem a atividade. Incentive o uso da calculadora. Se notar que a sala toda está parada no mesmo obstáculo, retome a atenção e faça algumas perguntas motivadoras como as que aparecem no guia de intervenção.
Propósito: O objetivo da atividade é fazer com que o aluno analise o uso da potência de decimal em uma situação prática, construindo significados para seu uso.
Discuta com a turma: Ao decorrer da atividade, faça perguntas à turma a respeito da potenciação e utilize a calculadora para explorar o conteúdo.
- Vocês perceberam alguma ligação entre o número de casas decimais e o expoente envolvido em cada operação?
- E se ao invés do desconto ser de 0,5 elevado ao número de erros fosse 0,15. Quantos pontos perderia Bruno?
- Nessa nova situação você percebe qual a relação entre o número de casas decimais e o expoente?
- O resultado do cálculo de uma potência sempre será um valor maior que a base?
- O que aconteceu quando elevamos 0,5 ao quadrado (expoente 2)? E quando elevamos 0,5 ao cubo (expoente 3)?
- O que acontece com a pontuação caso não ocorram erros ou acertos?
Discussão de Soluções (Slides 6 e 7)

Tempo sugerido: 10 minutos.
Orientação: Verifique com os alunos como eles resolveram as questões e as suas respostas. Utilize o quadro para listar as diferentes formas de raciocínio, mostrando também as que aparecem aqui nos slides. Dê ênfase aos erros e como eles podem construir caminhos para acertos.
Propósito: Comparar e discutir as soluções encontradas.
Discuta com a turma:
- Quais erros foram cometidos? Faça a análise dos seus erros. Por que eles ocorreram? O que é preciso fazer para consertá-los?
- Nas respostas dadas pelos personagens, existe algum erro? Alguém pensou e fez os cálculos como alguns dos personagens?
- Observe que quando lidamos com potências em que a base é um número entre zero e um e o expoente é natural, o resultado sempre é menor que a base. Observe que quanto mais erros são cometidos menos dinheiro é subtraído da mesada.
- Qual a potência quando o expoente é zero? Isso muda para bases maiores que 1 ou menores que 1?
- Bruno pode ficar com mesada “negativa”?
- Quais regras você utilizou para que os valores em reais tivessem apenas duas casas decimais? Você fez o arredondamento antes de subtrair os erros dos acertos ou depois?
Link Resolução: https://goo.gl/jHbR1e
Discussão de Soluções (Slides 6 e 7)

Tempo sugerido: 10 minutos.
Orientação: Verifique com os alunos como eles resolveram as questões e as suas respostas. Utilize o quadro para listar as diferentes formas de raciocínio, mostrando também as que aparecem aqui nos slides. Dê ênfase aos erros e como eles podem construir caminhos para acertos.
Propósito: Comparar e discutir as soluções encontradas.
Discuta com a turma:
- Quais erros foram cometidos? Faça a análise dos seus erros. Por que eles ocorreram? O que é preciso fazer para consertá-los?
- Nas respostas dadas pelos personagens, existe algum erro? Alguém pensou e fez os cálculos como alguns dos personagens?
- Observe que quando lidamos com potências em que a base é um número entre zero e um e o expoente é natural, o resultado sempre é menor que a base. Observe que quanto mais erros são cometidos menos dinheiro é subtraído da mesada.
- Qual a potência quando o expoente é zero? Isso muda para bases maiores que 1 ou menores que 1?
- Bruno pode ficar com mesada “negativa”?
- Quais regras você utilizou para que os valores em reais tivessem apenas duas casas decimais? Você fez o arredondamento antes de subtrair os erros dos acertos ou depois?
Encerramento

Tempo sugerido: 3 min
Orientação: Discuta com a turma sobre as atividades desenvolvidas e sobre o aprendizado adquirido.
Propósito: Concluir a aula, fazer uma revisão do que foi aprendido e das atividades desenvolvidas.
Discuta com a turma:
- Qual a opinião sobre a aula?
- O que acharam do conceito aprendido?
- Qual método que eles preferem para resolver a potência de decimal? Por quê?
- Quais as dificuldades encontradas?