Atividade principal
Plano de Aula
Plano de aula: Multiplicação e Divisão de Decimais
Plano 3 de uma sequência de 10 planos. Veja todos os planos sobre Descobrindo e ampliando as operações com racionais.
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Kurth Correa Waldhelm
Mentora: Débora Vieira de Moraes
Revisor: Rodrigo Morozetti Blanco
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF06MA10 - Resolver e elaborar problemas com números racionais positivos na representação decimal, envolvendo as quatro operações fundamentais e potenciação, por meio de estratégias diversas, utilizando estimativas e arredondamentos para verificar a razoabilidade de respostas, com e sem o uso de calculadora.
Objetivos específicos
Conceituar, resolver e elaborar estratégias de cálculo para multiplicação e divisão de números positivos na forma decimal.
Conceito-chave
Multiplicação e divisão de frações.
Recursos necessários
- Atividades impressas em folhas, coladas no caderno ou não;
- Papel e lápis para fazer anotações;
- Calculadora
Habilidades BNCC:
Objetivos de aprendizagem
Conceituar, resolver e elaborar estratégias de cálculo para multiplicação e divisão de números positivos na forma decimal.
Resumo da aula
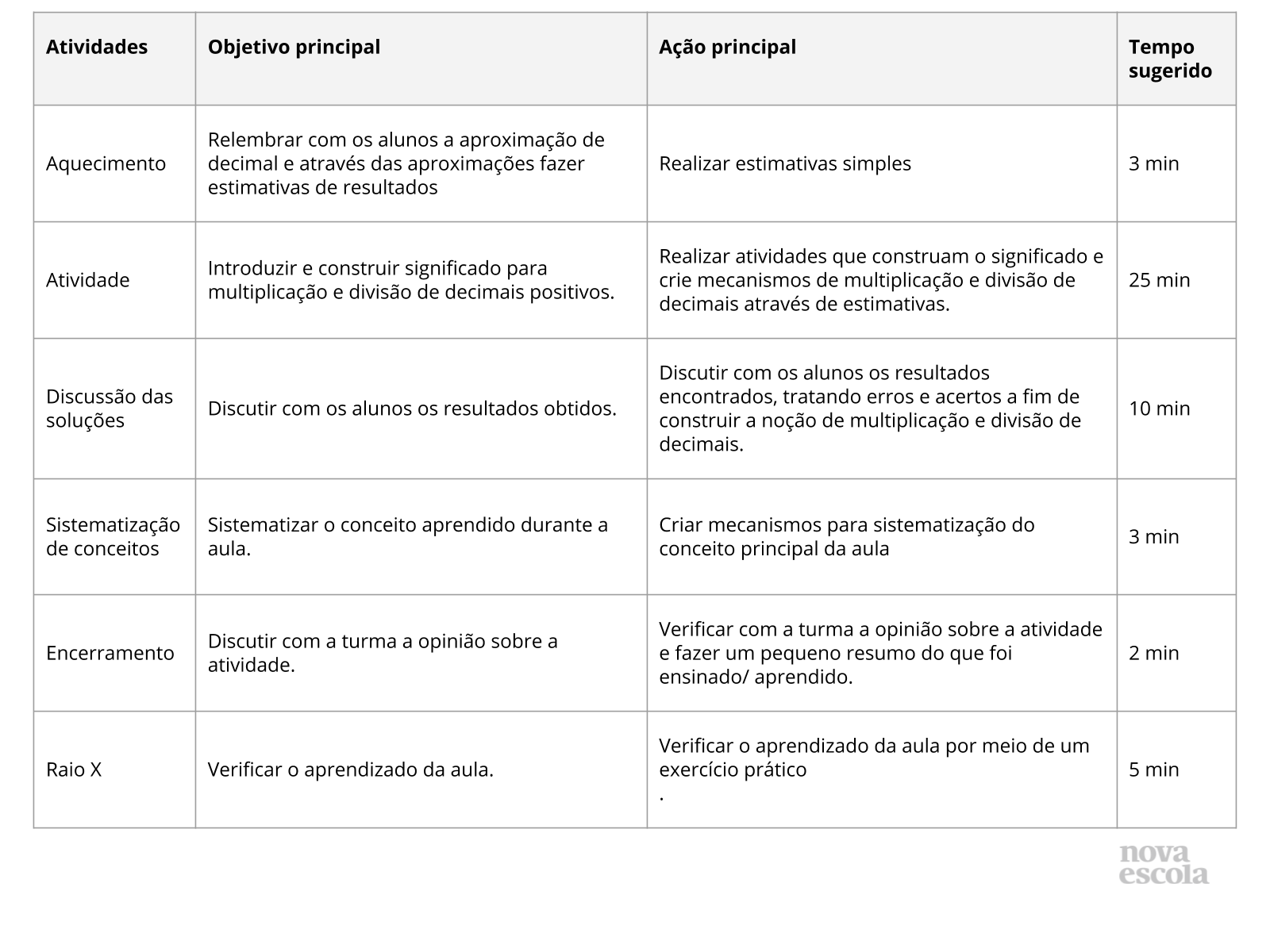 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Descreva para turma o objetivo da aula que é conceituar e construir significado para a multiplicação e divisão através da resolução de situações problemas, é importante ressaltar que o esforço produtivo dos alunos devem ser ressaltados a fim de que os mesmos sejam capazes de criar estratégias para multiplicar e dividir decimais.
Propósito: Relembrar conceitos já estudados utilizando-os para a construção do significado e entendimento de multiplicação e divisão de decimais. Na presente aula os alunos terão acesso a atividades que propiciam a construção deste aprendizado.
Aquecimento

Tempo sugerido: 3 minutos
Propósito: Relembrar com os alunos a aproximação de decimal e através das aproximações fazer estimativas de resultados.
Orientação: Se possível use o projetor ou faça um esboço deste slide no quadro. Espera-se que os alunos consigam lembrar sobre a aproximação de decimais ou que pelo menos consigam presumir qual é o inteiro mais próximo dos decimais apresentados.
Peça que pensem sobre o problema antes de dizer a resposta e em seguida escolha dois alunos para dizer as respostas (um para cada item) perguntado aos demais se eles concordam ou não com as respostas dadas.
No exercício (1) espera-se que todos percebam que 2,78 é próximo de 3 e que 2,78 x 5 é próximo de 15 (alternativa C). Por outro lado, no exercício (2), devem perceber que 14,4 : 2,1 é próximo de 14: 2 = 7 (alternativa C).
Discuta com a turma:
- Se em uma multiplicação de dois decimais eu aproximar os dois fatores para cima, o produto estimado será maior ou menor do que o produto exato? E se eu estimar os dois fatores para baixo? E se eu aproximar um para baixo e um para cima?
- Essas conclusões são válidas também para a divisão?
Atividade Principal

Tempo sugerido: 25 minutos (slides 4 a 6).
Propósito: Introduzir e construir significado para multiplicação e divisão de decimais positivos.
Orientação: Imprima a atividade para os alunos e se possível projete a mesma, para que todos possam acompanhar. Divida a classe em grupos e deixem que eles façam as atividades.
Na primeira parte (slide 4) a ideia é fazer com que eles, usando a calculadora, tirem conclusões sobre como operar com decimais. Já na segunda parte (slides 5 e 6), é preciso recolher as calculadoras e orientá-los para que, usando as conclusões anteriores, resolvam os desafios.
Caminhe pela sala, faça perguntas e, caso precise, recorra ao guia de intervenção em anexo.
Materiais complementares:
Atividade Principal

Tempo sugerido: 25 minutos (slides 4 a 6).
Propósito: Introduzir e construir significado para multiplicação e divisão de decimais positivos.
Orientação: Imprima a atividade para os alunos e se possível projete a mesma, para que todos possam acompanhar. Divida a classe em grupos e deixem que eles façam as atividades.
Na primeira parte (slide 4) a ideia é fazer com que eles, usando a calculadora, tirem conclusões sobre como operar com decimais. Já na segunda parte (slides 5 e 6), é preciso recolher as calculadoras e orientá-los para que, usando as conclusões anteriores, resolvam os desafios.
Caminhe pela sala, faça perguntas e, caso precise, recorra ao guia de intervenção em anexo.
Atividade Principal

Tempo sugerido: 25 minutos (slides 4 a 6).
Propósito: Introduzir e construir significado para multiplicação e divisão de decimais positivos.
Orientação: Imprima a atividade para os alunos e se possível projete a mesma, para que todos possam acompanhar. Divida a classe em grupos e deixem que eles façam as atividades.
Na primeira parte (slide 4) a ideia é fazer com que eles, usando a calculadora, tirem conclusões sobre como operar com decimais. Já na segunda parte (slides 5 e 6), é preciso recolher as calculadoras e orientá-los para que, usando as conclusões anteriores, resolvam os desafios.
Caminhe pela sala, faça perguntas e, caso precise, recorra ao guia de intervenção em anexo.
Discussão de Soluções

Tempo sugerido: 10 minutos. (Slides 7 a 9)
Propósito: Comparar e discutir com os alunos os resultados obtidos.
Orientação: Deixe que os alunos comparem suas respostas e observem as discordâncias, se houverem. Espera-se que todos acertem a tabela do slide 4, pois será feita na calculadora.
De acordo com a tabela, os alunos podem chegar a diferentes regras. Estimule-os a utilizar suas próprias estratégias, mas cuide para que não concluam estratégias erradas ou métodos que sirvam apenas para alguns exemplos e não para todos. Mostre o diálogo do slide 7 e pergunte se alguém concluiu algo similar ou algo diferente do que está escrito.
Utilize a conversa do slide 8 para pedir aos alunos que verifiquem suas regras nas operações propostas no problema de Daniel. Essas estratégias devem tê-los auxiliado na resolução do desafio.
Apenas ao chegar no slide 9 faça a correção dos itens a, b, c e d, pedindo a diferentes alunos que apresentem suas respostas e validem as respostas do colegas.
Discussão de Soluções

Tempo sugerido: 10 minutos. (Slides 7 a 9)
Propósito: Comparar e discutir com os alunos os resultados obtidos.
Orientação: Deixe que os alunos comparem suas respostas e observem as discordâncias, se houverem. Espera-se que todos acertem a tabela do slide 4, pois será feita na calculadora.
De acordo com a tabela, os alunos podem chegar a diferentes regras. Estimule-os a utilizar suas próprias estratégias, mas cuide para que não concluam estratégias erradas ou métodos que sirvam apenas para alguns exemplos e não para todos. Mostre o diálogo do slide 7 e pergunte se alguém concluiu algo similar ou algo diferente do que está escrito.
Utilize a conversa do slide 8 para pedir aos alunos que verifiquem suas regras nas operações propostas no problema de Daniel. Essas estratégias devem tê-los auxiliado na resolução do desafio.
Apenas ao chegar no slide 9 faça a correção dos itens a, b, c e d, pedindo a diferentes alunos que apresentem suas respostas e validem as respostas do colegas.
Discussão de Soluções

Tempo sugerido: 10 minutos. (Slides 7 a 9)
Propósito: Comparar e discutir com os alunos os resultados obtidos.
Orientação: Deixe que os alunos comparem suas respostas e observem as discordâncias, se houverem. Espera-se que todos acertem a tabela do slide 4, pois será feita na calculadora.
De acordo com a tabela, os alunos podem chegar a diferentes regras. Estimule-os a utilizar suas próprias estratégias, mas cuide para que não concluam estratégias erradas ou métodos que sirvam apenas para alguns exemplos e não para todos. Mostre o diálogo do slide 7 e pergunte se alguém concluiu algo similar ou algo diferente do que está escrito.
Utilize a conversa do slide 8 para pedir aos alunos que verifiquem suas regras nas operações propostas no problema de Daniel. Essas estratégias devem tê-los auxiliado na resolução do desafio.
Apenas ao chegar no slide 9 faça a correção dos itens a, b, c e d, pedindo a diferentes alunos que apresentem suas respostas e validem as respostas do colegas.
Sistematização

Tempo sugerido: 3 minutos (slides 10 e 11)
Propósito: Sistematizar o conceito aprendido durante a aula.
Orientação: Formalize junto à turma o conhecimento adquirido a fim de aplicá-lo a resoluções de situações problemas que envolvam essa temática. Deixe claro que as diferentes estratégias são válidas e podem ser matematicamente comprovadas.
Caso algum aluno tenha interesse, você pode passar como tarefa que ele refaça as operações utilizando frações decimais.
No caso da multiplicação (slide 10), ele deve observar que se há, por exemplo, décimos em um fator e centésimos no outro, haverá milésimos no produto (pois 10 x 100 = 1000).
No caso da divisão (slide 11) o raciocínio é diferente. A justificativa mais simples para a regra da divisão é levá-los a perceber que se multiplicarmos o dividendo por 10, o quociente também será multiplicado por 10. Entretanto, se multiplicarmos o divisor por 10, o quociente será dividido por 10 (pois quando dividimos o mesmo dividendo por um divisor maior, o quociente é proporcionalmente menor). Com isso deve ficar claro que se multiplicamos divisor e dividendo por 10 o quociente não se altera.
Sistematização

Tempo sugerido: 3 minutos (slides 10 e 11)
Propósito: Sistematizar o conceito aprendido durante a aula.
Orientação: Formalize junto à turma o conhecimento adquirido a fim de aplicá-lo a resoluções de situações problemas que envolvam essa temática. Deixe claro que as diferentes estratégias são válidas e podem ser matematicamente comprovadas.
Caso algum aluno tenha interesse, você pode passar como tarefa que ele refaça as operações utilizando frações decimais.
No caso da multiplicação (slide 10), ele deve observar que se há, por exemplo, décimos em um fator e centésimos no outro, haverá milésimos no produto (pois 10 x 100 = 1000).
No caso da divisão (slide 11) o raciocínio é diferente. A justificativa mais simples para a regra da divisão é levá-los a perceber que se multiplicarmos o dividendo por 10, o quociente também será multiplicado por 10. Entretanto, se multiplicarmos o divisor por 10, o quociente será dividido por 10 (pois quando dividimos o mesmo dividendo por um divisor maior, o quociente é proporcionalmente menor). Com isso deve ficar claro que se multiplicamos divisor e dividendo por 10 o quociente não se altera.
Encerramento

Tempo sugerido: 2 minutos.
Propósito: Obter a opinião da turma sobre a atividade e verificar se todos acompanharam os exercícios.
Orientação: Discuta com a turma sobre as atividades desenvolvidas e sobre o aprendizado adquirido. Verifique se todos compreendem os exemplos dados e se se apropriaram de suas estratégias.
Raio X

Tempo sugerido: 10 minutos.
Propósito: Verificar o aprendizado do aluno na aula.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem, utilizando as fichas. Em seguida faça um levantamento dos resultados obtidos e discuta as estratégias de resolução.
Materiais complementares para impressão:
Para os alunos
Para o professor
Sugestão de adaptação para ensino remoto
Código do plano
MAT6_06NUM03
Recursos
- Necessários: Caderno, lápis, borracha, calculadora, grupo de WhatsApp
- Opcionais: Khan Academy :https://pt.khanacademy.org/math/algebra-basics/basic-alg-foundations/alg-basics-operations-with-decimals/v/multiplying-decimals
Para este plano, foque na etapa Aquecimento e Atividade Principal.
Aquecimento
Professor, inicie essa aula organizando os alunos em quartetos. Explique a eles que deverão fazer uma videochamada de grupo pelo WhatsApp e que eles terão cerca de 10 minutos para fazer a atividade proposta no Aquecimento. Compartilhe o slide do Aquecimento com eles e combine o horário de retorno ao grande grupo, para que possam compartilhar suas conclusões. Ao retornarem para o grande grupo, explore bem esse momento. Instigue os alunos a analisar os processos de cálculo de estimativa, se houve arredondamento, se foi para mais e de que forma isso influencia nos cálculos. Garanta que cada grupo consiga compartilhar suas conclusões. Peça aos alunos de cada grupo que acionem seus microfones para explicar suas estratégias. Caso sua aula não seja síncrona, encaminhe essas atividades de forma remota, por um meio de comunicação combinado entre vocês (WhatsApp, por exemplo) e solicite que enviem um áudio para o grande grupo explicando suas conclusões. Posteriormente, envie um áudio com a devolutiva dessa atividade.
Atividade Principal
Dando continuidade, considerando uma aula síncrona, compartilhe com os alunos o primeiro slide da Atividade Principal e oriente-os a realizar o que está proposto. Eles podem realizar essa atividade em grupo, da mesma forma como foi feito anteriormente. Ao retornarem para o grande grupo solicite que compartilhem suas conclusões e ajude-os a organizar as ideias em relação ao que acontece com as casas decimais na multiplicação e na divisão de números decimais. Nos slides 5 e 6 da atividade principal, solicite que deixem a calculadora para realizarem as atividades propostas usando o cálculo mental e a estimativa.
Discussão das soluções
A discussão das soluções é uma etapa importantíssima da aula. É o momento de justificar as estratégias e respostas usadas para a resolução do problema proposto na atividade principal. Faça boas perguntas, usando as orientações dos próprios slides da atividade principal. Estimule os alunos a usar uma ferramenta de áudio ou vídeo e falar como pensaram para atender o que foi solicitado e o que acham das colocações dos personagens no segundo slide da atividade principal. Pergunte como eles pensaram e peça que compartilhem suas estratégias. Estimule os alunos a perceberem que podemos seguir por diversos caminhos para chegar a uma solução e que o erro faz parte do processo de aprendizagem. Assim, você estará combatendo a valorização excessiva da resposta certa. Lembre-se que o objetivo da aula é que os alunos compreendam a multiplicação e a divisão de números na forma decimal. Sendo assim, explore essa atividade para que eles possam perceber a regularidade presente nessa proposta, sistematizando esse conteúdo. Garanta que o encerramento seja feito nessa etapa.
Convite às famílias
Peça às famílias que, oportunamente, auxiliem na leitura das comandas e no envio das soluções, conforme os combinados com o professor. É importante que as famílias acompanhem as atividades nos canais de comunicação estabelecidos entre vocês. Sugira aos alunos que convidem seus familiares para assistir ao vídeo sobre multiplicação de números decimais da Khan Academy através do link https://pt.khanacademy.org/math/algebra-basics/basic-alg-foundations/alg-basics-operations-with-decimals/v/multiplying-decimals
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Kurth Correa Waldhelm
Mentora: Débora Vieira de Moraes
Revisor: Rodrigo Morozetti Blanco
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF06MA10 - Resolver e elaborar problemas com números racionais positivos na representação decimal, envolvendo as quatro operações fundamentais e potenciação, por meio de estratégias diversas, utilizando estimativas e arredondamentos para verificar a razoabilidade de respostas, com e sem o uso de calculadora.
Objetivos específicos
Conceituar, resolver e elaborar estratégias de cálculo para multiplicação e divisão de números positivos na forma decimal.
Conceito-chave
Multiplicação e divisão de frações.
Recursos necessários
- Atividades impressas em folhas, coladas no caderno ou não;
- Papel e lápis para fazer anotações;
- Calculadora