Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
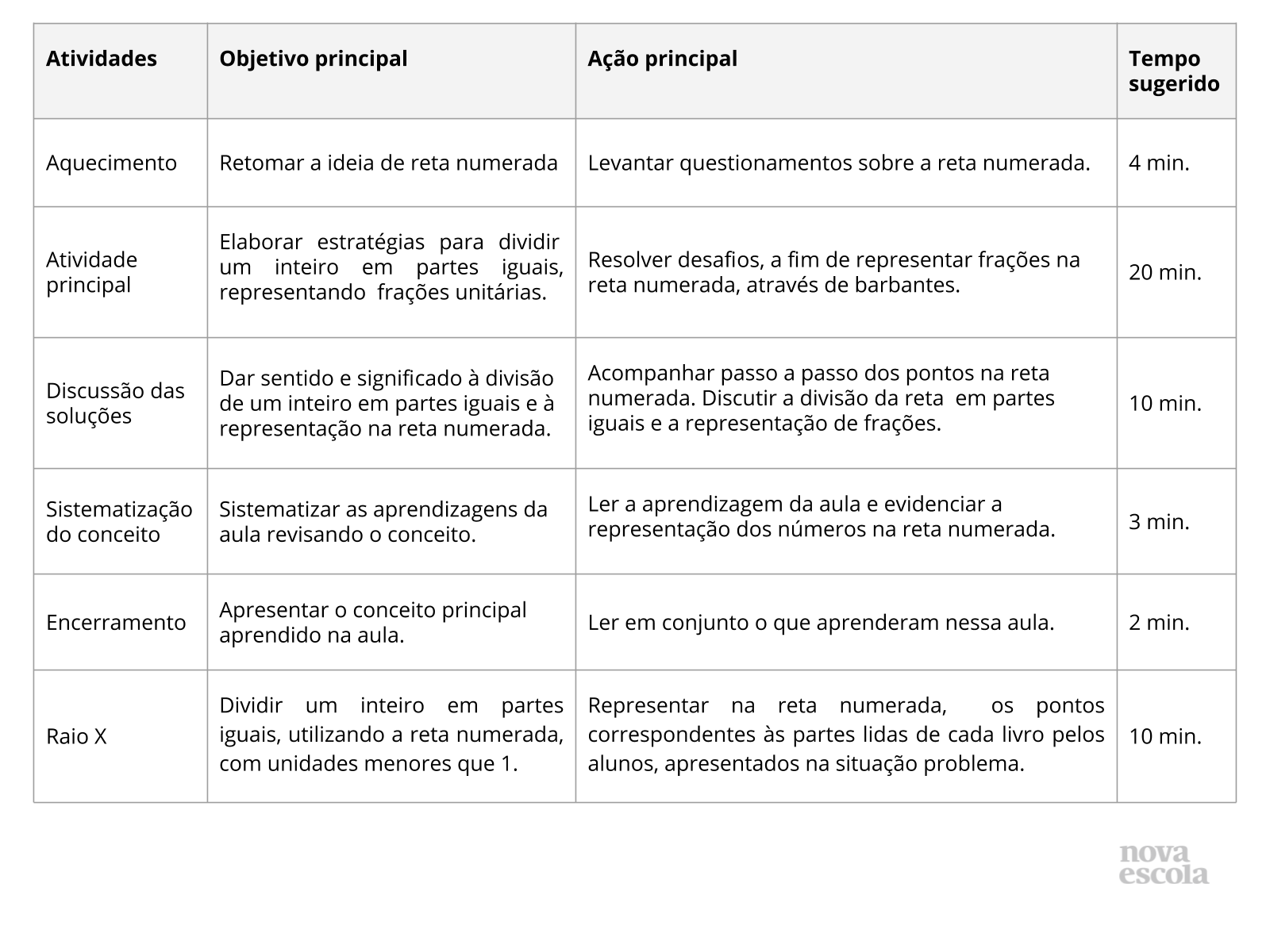
Aquecimento

Tempo sugerido: 4 minutos.
Orientação: Projete ou leia as perguntas para a turma.
Propósito: Levantar questionamentos sobre a reta numerada e tipos de retas existentes.
Discuta com a turma:
- Você já viu uma reta numerada?
- Sabe para o que serve?
- Você sabe como é a estrutura de uma reta numerada?
- Quais tipos de retas numeradas você conhece?
- Há objetos que lembram uma reta numerada? (régua, termômetro…)
- Para o que servem essas retas?
- Você já utilizou uma dessas retas em alguma situação da sua vida?
- Em uma reta numerada, você consegue identificar o ponto de origem? E o de término?
Atividade Principal

Tempo sugerido: 20 minutos .
Orientações: Divida a turma em pequenos grupos de dois ou quatro alunos. Distribua pedaços de barbantes para os alunos e comece a aula levantando questões sobre a representação de frações, utilizando os barbantes. É importante que os pedaços de barbante sejam iguais. Peça que cada dupla ou grupo segure o pedaço de barbante bem esticado e represente as frações determinadas dando nós no barbante. Os alunos podem colorir com hidrocor de cores diferentes cada nó e fazer uma legenda ou o professor pode apresentar uma legenda para cada ponto (nó) que for realizado. Além das frações indicadas no slide, trabalhe com outras frações de denominadores 2 ou 4.
Propósito: Fazer com que os alunos pensem nas possibilidades representar frações, dividindo um inteiro (barbante) em partes iguais.
Discuta com a turma:
- Quais estratégias podemos utilizar para representarmos uma fração nos barbantes?
- Por que para representar a fração precisamos dividir o barbante?
- O que significa representar a fração ½ no barbante? Em quantas partes o barbante foi dividido?
- E a fração ¼?
- Alguém pode vir à frente demonstrar como fez? Como seu grupo pensou para representar dessa forma?
- Para representar a fração ¾ como podemos fazer? Em quantas partes o barbante será dividido?
Atividade principal
Resolução da atividade
Guia de intervenção
Atividade Principal

Tempo sugerido: 20 minutos .
Orientações: Utilize os mesmos pedaços de barbante que foram distribuídos para os grupos de dois ou quatro alunos. Peça para que os alunos considerem a ponta do lado esquerdo do barbante como o ponto 0 e a ponta do lado direito do barbante como o ponto 1. Lance desafios aos alunos com perguntas:
- Imaginando que o barbante seja uma reta numerada, onde localizamos o ponto 1/ 2?
- E o ponto 1/4?
- E o ponto 3/4?
Continue lançando desafios aos alunos de forma que eles tenham que encontrar os pontos ditados por você, no barbante, dando nós de cores diferentes de acordo com a legenda que colocará no quadro. Eleve o nível das perguntas a cada rodada. Trabalhe também com frações impróprias, como, 7/4, 5/2 deixando outros pedaços de barbante do mesmo tamanho disponíveis para que aumentem a reta numerada emendando o barbante e, consequentemente aumentando o intervalo de 0 a 1 para 0 a 2 ou 0 a 3 dependendo da fração que for pedida.
- Para representar a fração 7/4 um barbante é suficiente? Como podemos fazer?
- Como podemos marcar esse ponto?
Peça para que os alunos, primeiramente, pensem nas respostas, individualmente e depois discuta com o grupo. Ao final da discussão respondam a qual conclusão o grupo chegou. Após, peça para que os alunos registrem no caderno reproduzindo o barbante e os desafios lançados em forma de reta numerada.
Propósito: Elaborar estratégias para dividir um inteiro (barbante) em partes iguais, representando frações unitárias.
Discuta com a turma:
- Para representarmos uma fração a partir de um inteiro, como devemos fazer utilizando a reta numerada?
- Em nossa atividade, qual é o nosso inteiro?
- Qual é a diferença entre a reta numerada que representa um meio e a que representa um quarto?
- Como podemos representar uma fração imprópria utilizando o barbante?
- E utilizando a reta numerada?
Material Complementar para o professor:
http://escolakids.uol.com.br/reta-numerica.htm
http://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-reta-numerica.htm
- Frações em uma reta numérica
https://pt.khanacademy.org/math/arithmetic/fraction-arithmetic/arith-review-fractions-on-the-number-line/v/fractions-on-a-number-line
Discussão de solução
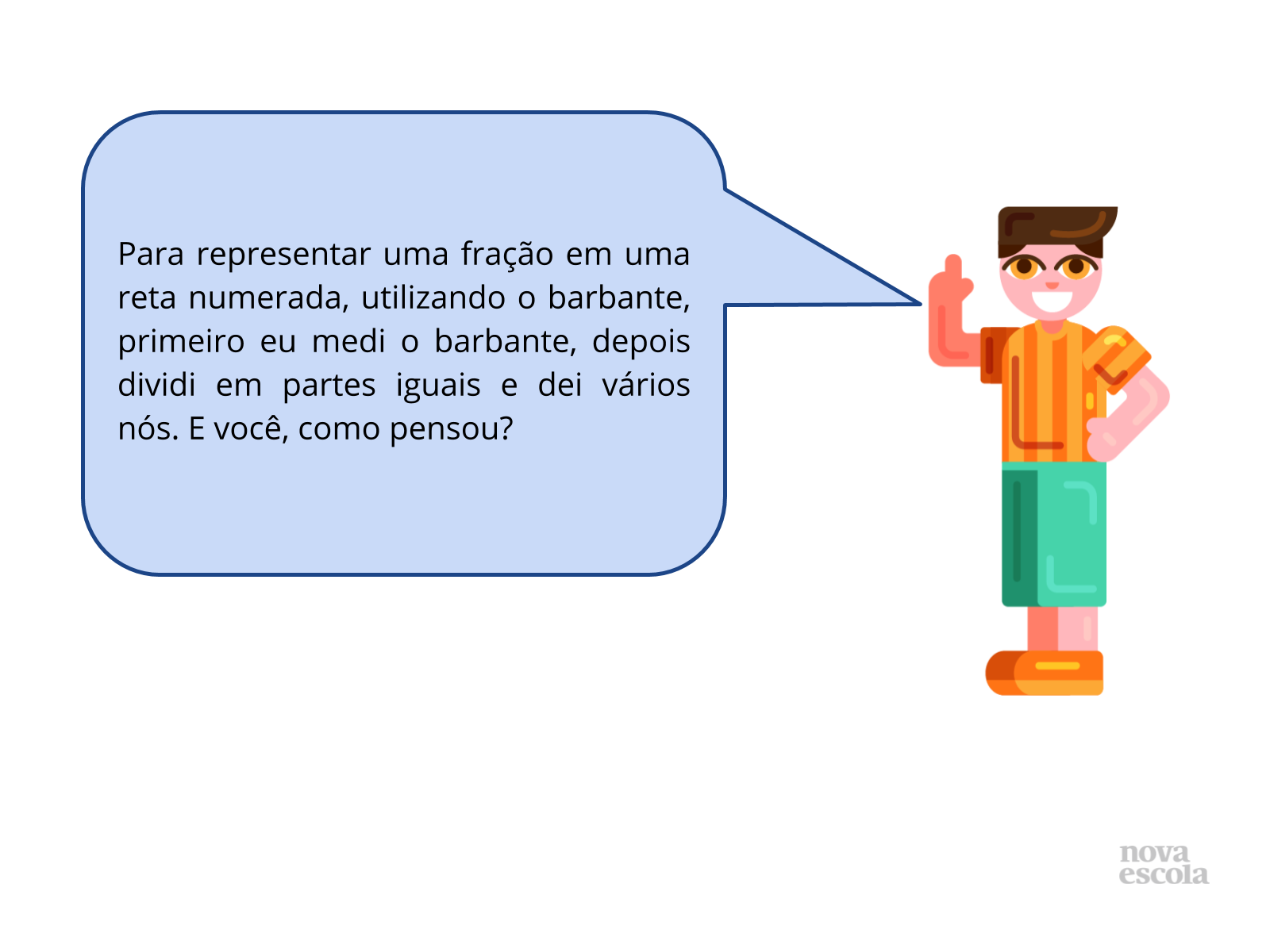
Tempo sugerido: 10 minutos.
Orientação: Projete ou leia a pergunta para a turma. Propicie oportunidades dos alunos exporem suas ideias, a forma com que pensaram, quais estratégias utilizaram e a qual conclusão chegaram.
Propósito: Discutir com a turma as possibilidades de construir uma reta numerada, dividindo um inteiro em partes iguais.
Discuta com a turma:
- Quais estratégias podemos utilizar para representar as frações, utilizando os barbantes?
- Alguém pode demonstrar?
- Quais dificuldades encontraram para resolver os desafios? Como solucionaram o impasse?
- Como representaram, no caderno, os desafios, através da reta numerada?
- Houve divergências de opiniões para as soluções dos desafios, no grupo? Como solucionaram?
Discussão de solução
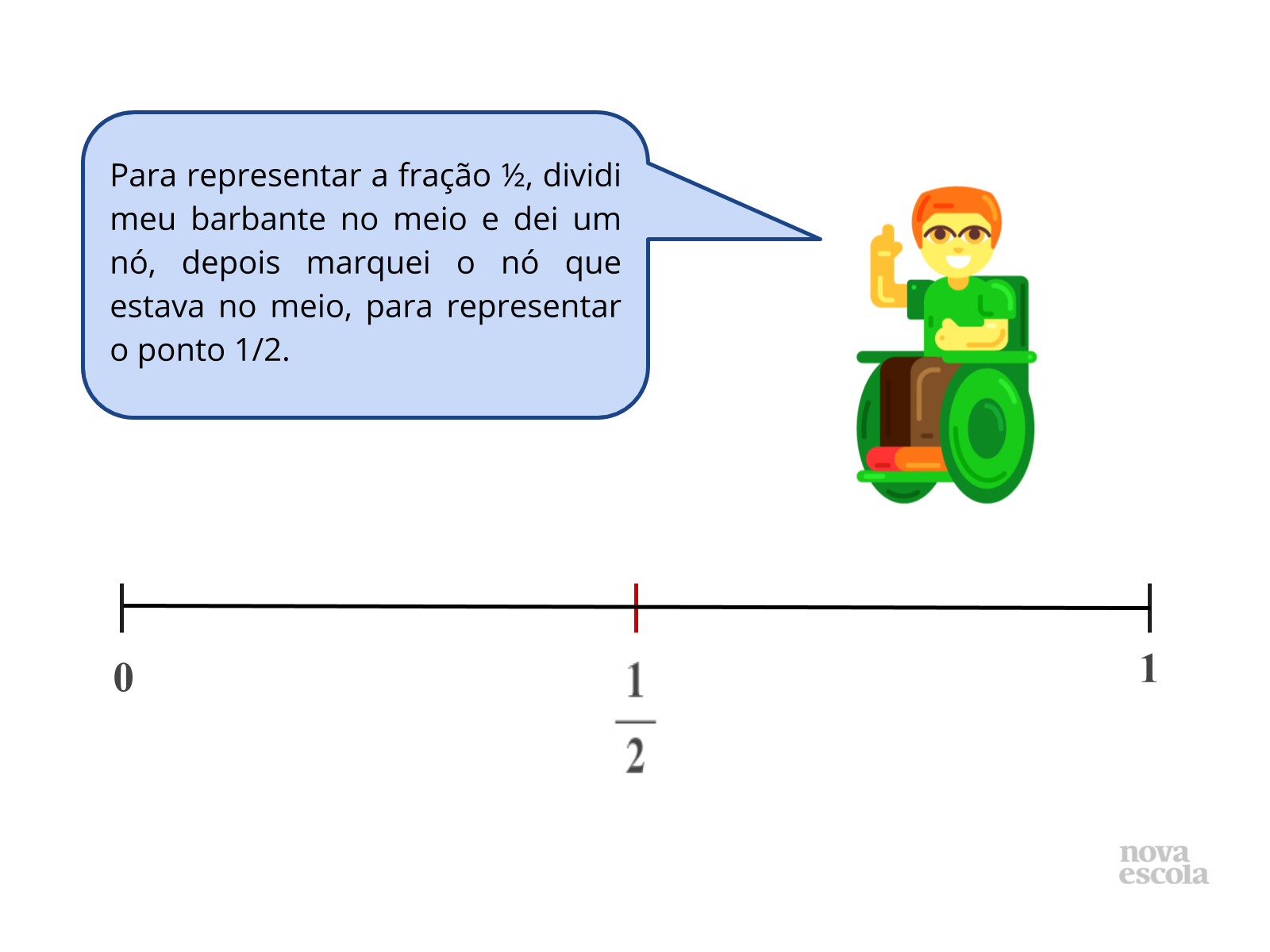
Tempo sugerido: 10 minutos.
Orientação: Projete ou leia a pergunta para a turma. Propicie oportunidades dos alunos exporem suas ideias, a forma com que pensaram, quais estratégias utilizaram e a qual conclusão chegaram.
Propósito: Discutir com a turma as possibilidades de construir uma reta numerada, dividindo um inteiro em partes iguais.
Discuta com a turma:
- Quais estratégias podemos utilizar para representar as frações, utilizando os barbantes?
- Alguém pode demonstrar?
- Quais dificuldades encontraram para resolver os desafios? Como solucionaram o impasse?
- Como representaram, no caderno, os desafios, através da reta numerada?
- Houve divergências de opiniões para as soluções dos desafios, no grupo? Como solucionaram?
Discussão de solução

Tempo sugerido: 10 minutos.
Orientação: Projete ou leia a pergunta para a turma. Propicie oportunidades dos alunos exporem suas ideias, a forma com que pensaram, quais estratégias utilizaram e a qual conclusão chegaram.
Propósito: Discutir com a turma as possibilidades de construir uma reta numerada, dividindo um inteiro em partes iguais.
Discuta com a turma:
- Quais estratégias podemos utilizar para representar as frações, utilizando os barbantes?
- Alguém pode demonstrar?
- Quais dificuldades encontraram para resolver os desafios? Como solucionaram o impasse?
- Como representaram, no caderno, os desafios, através da reta numerada?
- Houve divergências de opiniões para as soluções dos desafios, no grupo? Como solucionaram?
Sistematização do conceito

Tempo sugerido: 3 minutos.
Orientação: Sistematize o conteúdo retomando com os estudantes o conceito de reta numerada.
Propósito: Sistematizar os conceitos que foram apresentados na aula.
Encerramento

Tempo sugerido: 2 minutos.
Orientações: Encerre a atividade retomando com os estudantes os conceitos estudados nessa aula.
Propósito: Revisar o conceito estudado.
Raio X

Tempo sugerido: 10 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem. Circule pela sala, observando como cada criança realiza a atividade e procure não dar respostas prontas, mas sim fazê-los encontrar as respostas pela reflexão. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando as soluções na lousa.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito da representação fracionária na reta numerada.
Discuta com a turma:
- De que maneira você chegou às respostas?
- Quais foram seus pontos fortes e fracos nessa aula?
- Qual é o seu plano para melhorar onde teve mais dificuldade?
Materiais complementares:
Raio X para impressão
Resolução do Raio X
Atividade complementar
Resolução da Atividade complementar
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.