Sugestão de adaptação para ensino remoto
Código do plano (MAT9_08ALG08)
Ferramentas sugeridas
- Essenciais: Alguma rede social (Whatsapp, Facebook, etc.) e papel para anotações.
- Optativas: Calculadora, cronômetro.
Aquecimento
- Pela rede social escolhida, chame a atenção para as maneiras de descrever as relações cotidianas e científicas que, normalmente, usamos as fórmulas e linguagens algébricas. Questione: “mas será que existem outras formas?”.
Atividade principal
- Determine a pesquisa de diversos tipos de gráficos usados para relatar as coisas cotidianas e científicas, e peça que produzam um parágrafo relatando quais tipos são mais empregados em cada tipo de contexto;
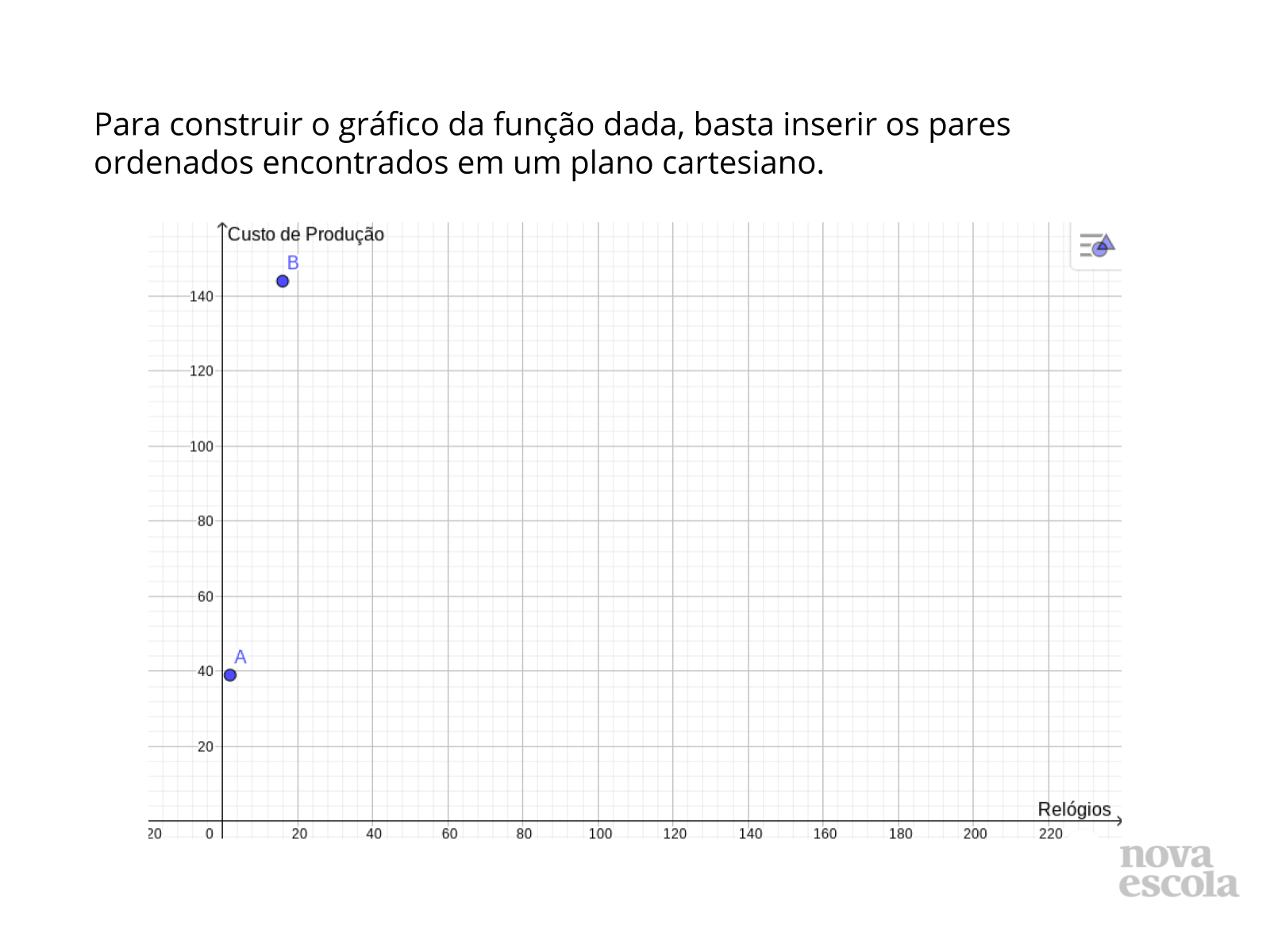
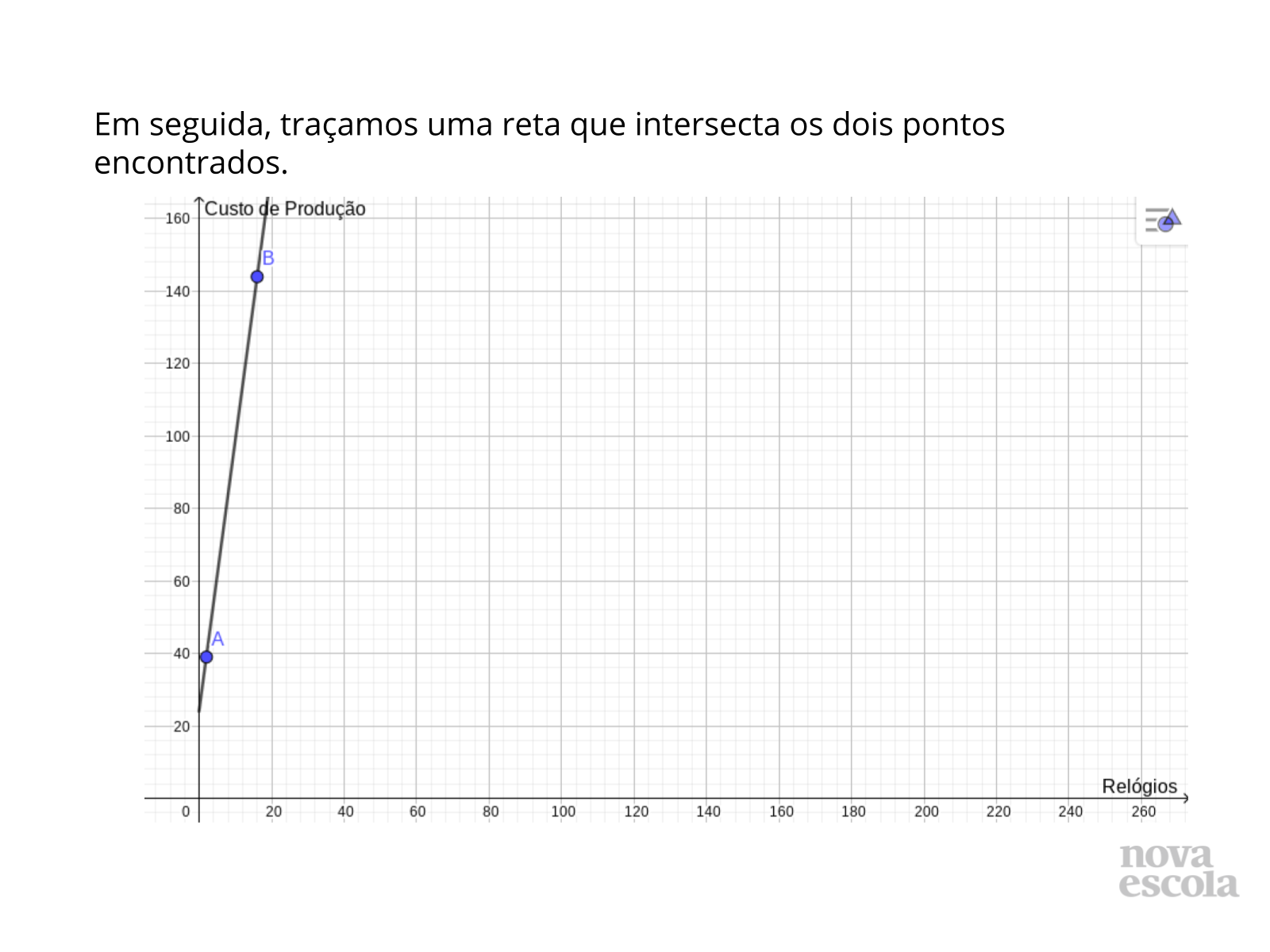
- No retorno da pesquisa, peça para construírem o gráfico de uma função relativo à situação abaixo, dando pelo menos 4 valores para as quantidades de relógios, e relatando o domínio, contradomínio e imagem desse recorte de valores escolhidos:
“Numa fábrica de relógios, o custo de produção de um determinado modelo de relógio é de R$ 7,50 por unidade, mais um custo inicial de R$ 24,00.”
Painel de soluções
- Espera-se que apareçam fórmulas que, no fim das contas, seja equivalente a:
f(x) = 7,5x + 24
- Espera-se que descrevam o domínio como o conjunto dos naturais, o contra-domínio poderia ser os reais ou só os racionais dariam conta e a imagem depende dos 4 valores assumidos por cada um.
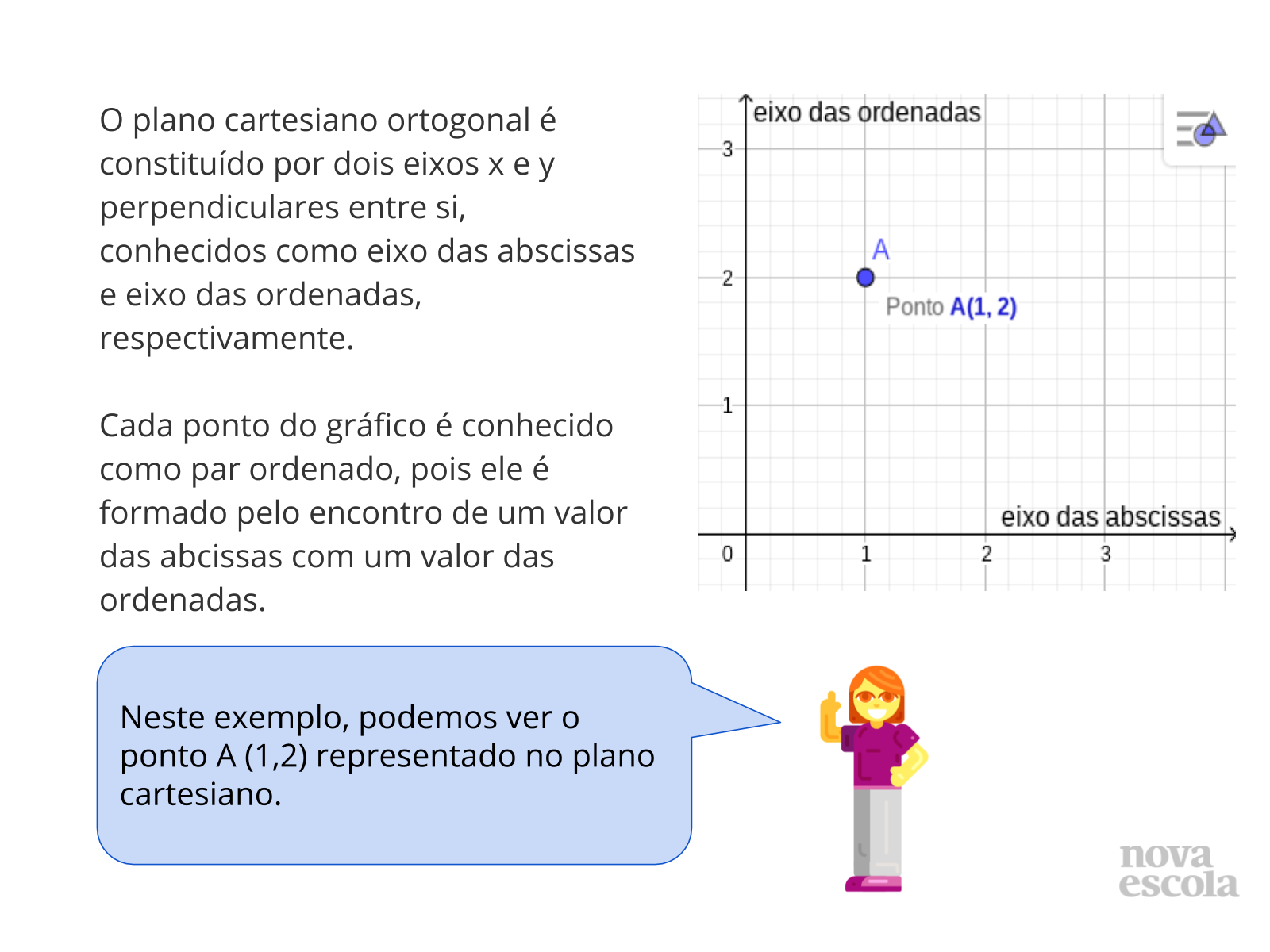
- Espera-se que marquem pontos no plano cartesiano SEM FAZER A LIGAÇÃO POR MEIO DE UMA RETA.
Discussão das soluções
- Na discussão das soluções, reforce que o tipo de domínio e imagem, determinam como será o gráfico, se será contínuo ou não.
Sistematização e encerramento
- Faça uma sistematização dizendo que, quando usamos uma função inserida numa outra função, chamamos de função composta e representamos por f(g(x)) ou f o g.
Raio X
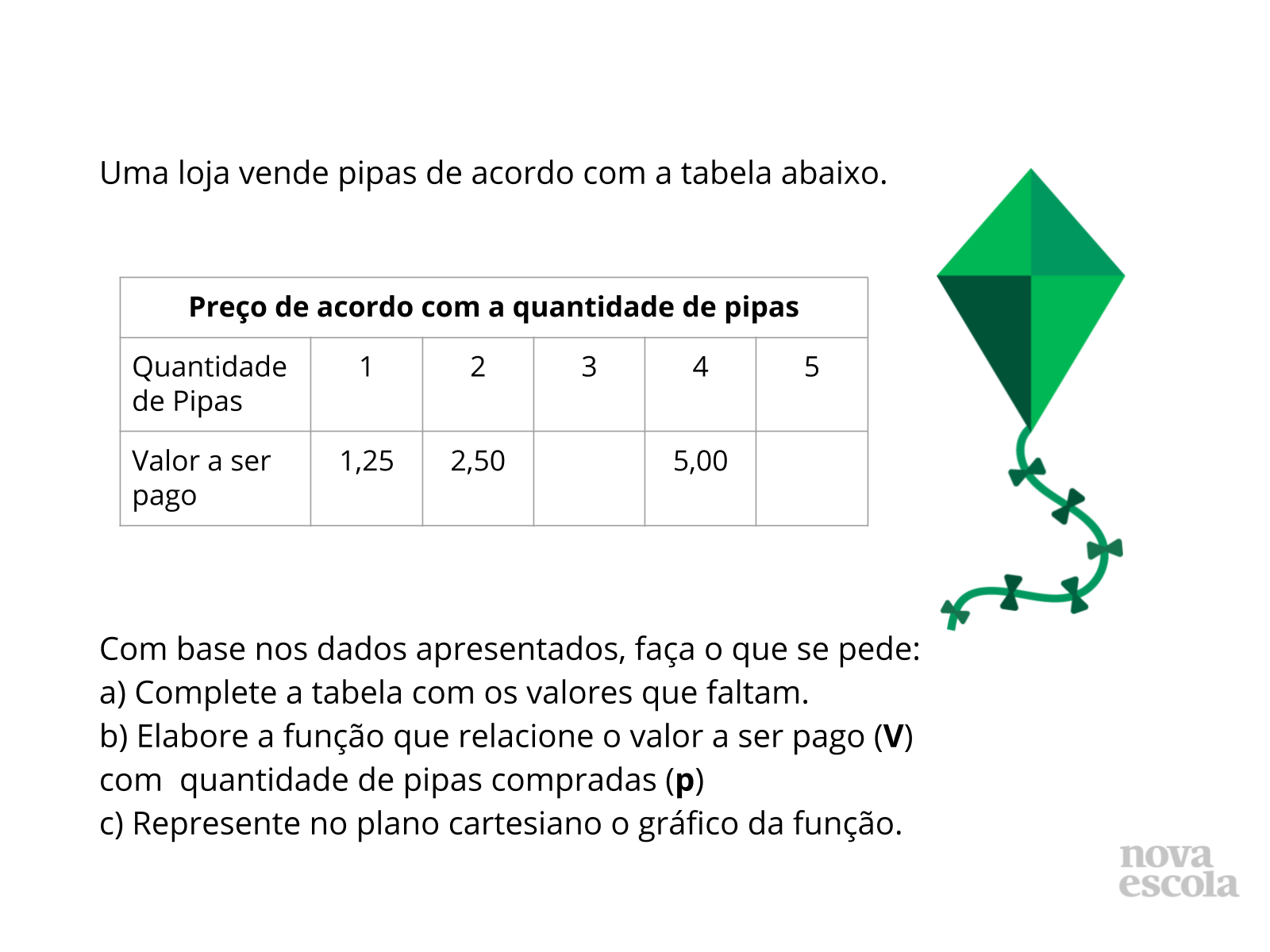
- Determine que pensando na situação apresentada na tabela abaixo, respondam às perguntas que se seguem:

Com base nos dados apresentados, faça o que se pede:
a) Complete a tabela com os valores que faltam.
b) Elabore a função que relacione o valor a ser pago (V) com quantidade de pipas compradas (p)
c) Represente no plano cartesiano o gráfico da função.
Convite às famílias
Peça para que seus alunos envolvam seus familiares, próximos neste momento, e relatem suas pesquisas sobre gráficos e proponham que tentem representar algumas situações cotidiana por meio deles, ainda que de maneira estimativa.
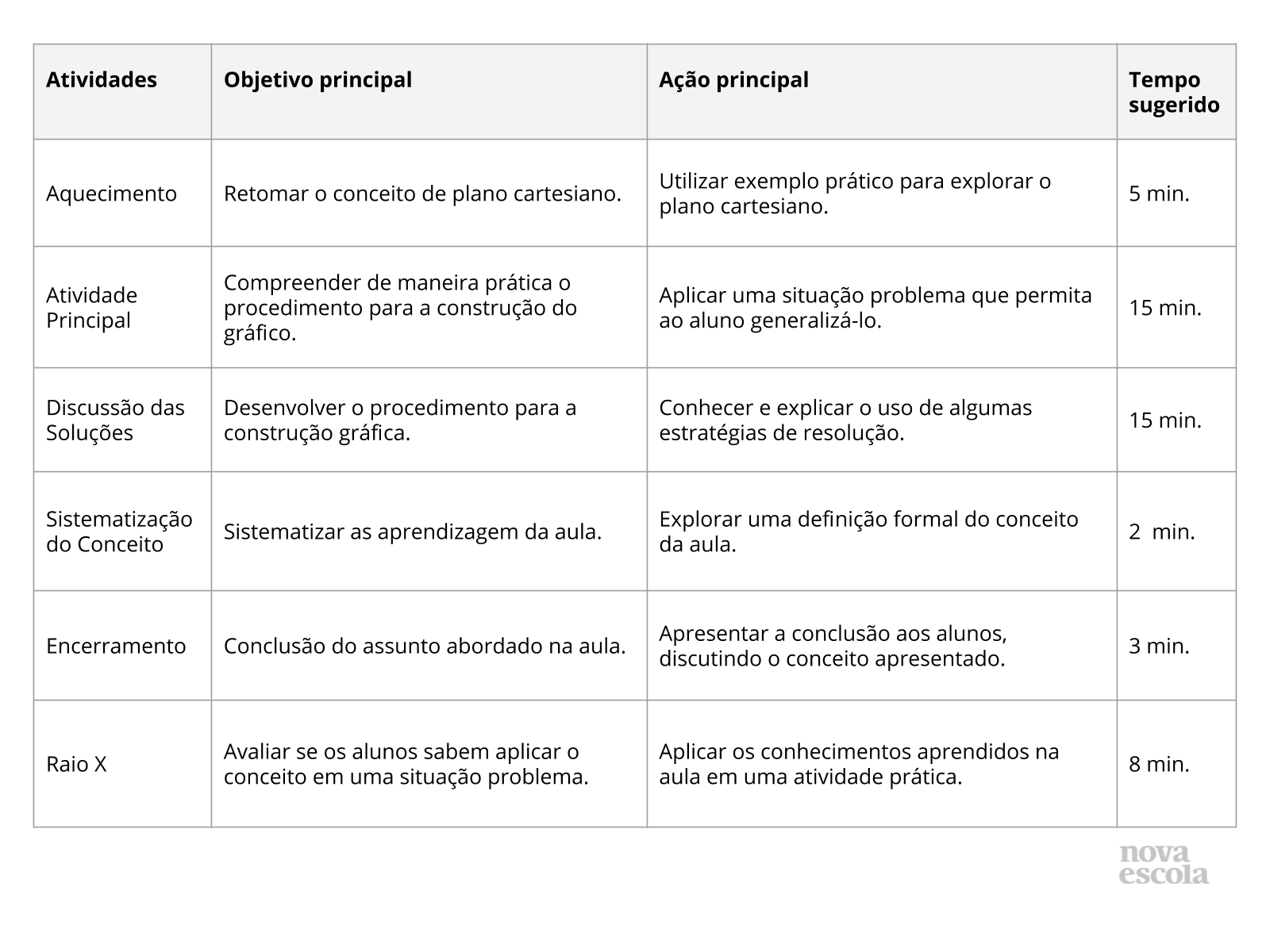 Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.