Atividade principal
Plano de Aula
Plano de aula: Resolvendo equações quadráticas por fatoração
Plano 2 de uma sequência de 10 planos. Veja todos os planos sobre Equações quadráticas
Tem interesse no tema "Neurociência, adolescências e engajamento nos Anos Finais"?
Inscreva-se neste tema para receber novidades pelo site e por email.
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Lais Aline Casagrande Pires de Melo
Mentor: Telma Regina França Rosso
Especialista de área: Sandra Amorim
Habilidade da BNCC
EF09MA09 - Compreender os processo de fatoração de expressões algébricas, com base em suas relações com os produtos notáveis, para resolver e elaborar problemas que possam ser representados por equações polinomiais do 2º Grau.
Objetivos específicos
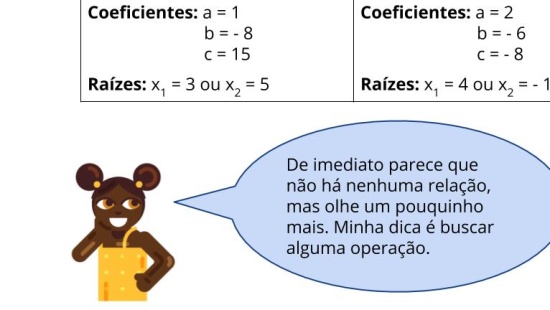
Relacionar a fatoração com a resolução de equações quadráticas.
Conceito-chave
Fatorar e resolver equações quadráticas.
Conceitos que a turma deve dominar
- Identificar monômios, binômios e trinômios
- Realizar a fatoração
- Identificar uma equação quadrática
Recursos necessários
- Projetor (pode ser substituído pelo quadro)
- Atividades impressas
- Caderno e Lápis
Habilidades BNCC:
Objetivos de aprendizagem
Relacionar a fatoração com a resolução de equações quadráticas.

Precisa de ajuda para criar uma aula personalizada?
Crie seu plano de aula em menos de um minuto no WhatsApp.
Novo curso gratuito

Conheça nosso mais novo curso sobre adolescências, neurociência e engajamento nos anos finais
VER CURSO