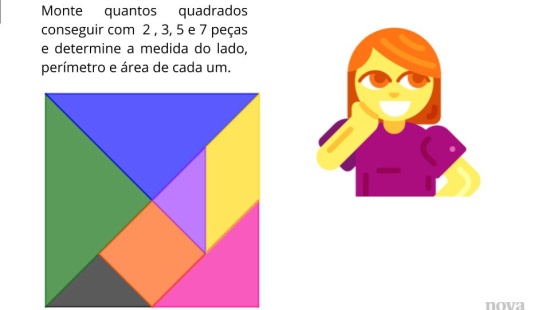
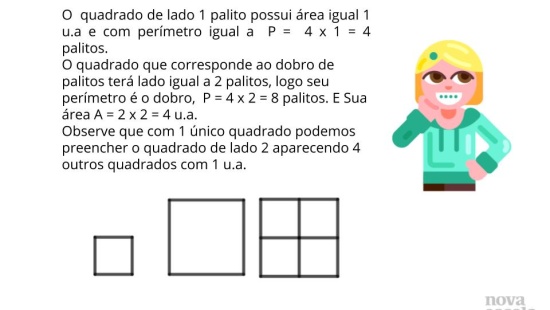
Atividade Principal
Plano de Aula
Plano de aula: Lado, perímetro e área de um quadrado, uma charada
Plano 4 de uma sequência de 5 planos. Veja todos os planos sobre Área e Perímetro do quadrado: quem é proporcional?
Por: Elizabeth Bento
Tem interesse no tema "Neurociência, adolescências e engajamento nos Anos Finais"?
Inscreva-se neste tema para receber novidades pelo site e por email.
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Elizabeth Bento
Mentor: Maria Aparecida Nemet
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF06MA27) Analisar e descrever as mudanças que ocorrem no perímetro e área de um quadrado quando ampliamos ou reduzimos seus lados por um fator k.
Habilidades necessárias
Determinar perímetro e área de um quadrilátero, reconhecer quando há proporcionalidade entre duas grandezas, escrever múltiplos.
Objetivos específicos
Concluir que apenas lado e perímetro de um quadrado são proporcionais. Reconhecer que os fatores que ampliam ou reduzem os lados de um quadrado não são os mesmos que ampliam ou reduzem as áreas, constando a existência ou não da proporcionalidade.
Conceito-chave
Área, perímetro, proporcionalidade, múltiplos.
Recursos necessários
- canetão
- sulfite
Habilidades BNCC:
Objetivos de aprendizagem
Concluir que apenas lado e perímetro de um quadrado são proporcionais. Reconhecer que os fatores que ampliam ou reduzem os lados de um quadrado não são os mesmos que ampliam ou reduzem as áreas, constando a existência ou não da proporcionalidade.
Planeje suas aulas pelo Whatsapp!
Qualidade com economia de tempo
Aula
Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo
Tempo sugerido: 2 minutos.
Orientação: Compartilhe o objetivo da aula com a classe.
Propósito: Compartilhar o objetivo da aula e motivá-los ao estudo.
Novo curso gratuito
Conheça nosso mais novo curso sobre adolescências, neurociência e engajamento nos anos finais
VER CURSO
