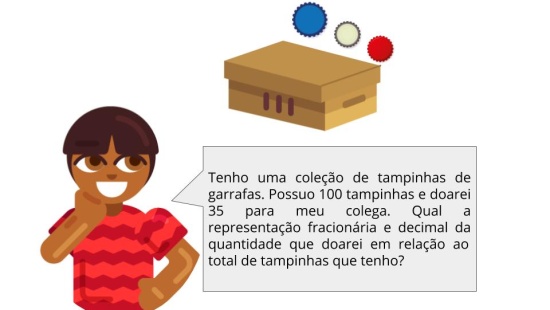
Atividade principal
Plano de Aula
Plano de aula: A reta numerada e os números decimais.
Plano 7 de uma sequência de 10 planos. Veja todos os planos sobre Números racionais nas suas formas fracionária e decimal
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Cátia do Vale dos Santos Mendes
Mentor: Sônia Maria dos Santos Campos Neves
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF05MA02 - Ler, escrever e ordenar números racionais na forma decimal com compreensão das principais características do sistema de numeração decimal, utilizando, como recursos, a composição e decomposição e a reta numérica.
Objetivos específicos
Identificar a localização dos números na reta numerada;
Representar números decimais na reta numerada.
Conhecimentos Prévios:
Representação decimal na reta numerada.
Conceito-chave
Representação de números decimais na reta numerada.
Recursos necessários
- Caderno,
- atividade impressa,
- fita métrica,
- lápis de cor,
- lápis de escrever,
- régua,
- trena
- borracha.
Habilidades BNCC:
Objetivos de aprendizagem
Identificar a localização dos números na reta numerada;
Representar números decimais na reta numerada.

Precisa de ajuda para criar uma aula personalizada?
Crie seu plano de aula em menos de um minuto no WhatsApp.