Guia de intervenções
Plano de Aula
Plano de aula: Elaboração de problemas
Plano 5 de uma sequência de 5 planos. Veja todos os planos sobre Problemas de multiplicação e divisão através de estratégias pessoais
Descrição
Este plano de aula foi elaborado pelo Time de autores NOVA ESCOLA
Autora: Ináldia Viana da Silva Sabino
Mentora: Eliane Zanin
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
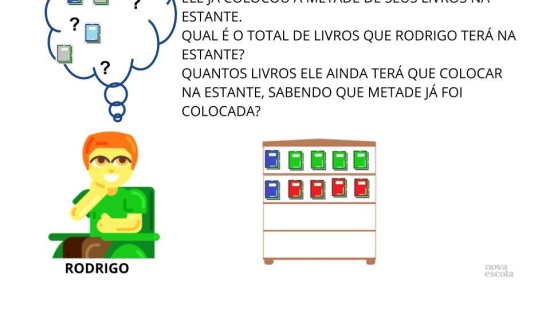
(EF03MA08) Resolver e elaborar problemas de divisão de um número natural por outro (até 10) com resto zero e diferente de zero, com os significados de repartição equitativa e de medida, por meio de estratégias pessoais.
Conhecimento prévio que a turma deve dominar:
Contar a quantidade de objetos de coleções até 100 unidades e apresentar o resultado por registros verbais e simbólicos;
Resolver e elaborar problemas envolvendo as ideias de divisão, com suporte de imagens e/ou material manipulável, utilizando estratégias pessoais.
Objetivo específico:
Resolver operações de divisão equitativa de um número natural por outro com resto diferente de 0.
Conceito-chave:
Divisão equitativa com resto diferente de O.
Recursos necessários:
_ Equipamento de projeção de imagem;
_ Cartazes;
_ Atividade xerocada;
_ Papel;
_ Lápis e
_ Materiais manipulativos.
Habilidades BNCC:
Objetivos de aprendizagem

Precisa de ajuda para criar uma aula personalizada?
Crie seu plano de aula em menos de um minuto no WhatsApp.
Um novo aliado para Professores Alfabetizadores

Acompanhe o progresso dos alunos durante o ano e otimize seu planejamento
ACESSAR AGORA