Guia de intervenção
Plano de Aula
Plano de aula: Cálculo mental com múltiplos de 10 - Divisão
Plano 3 de uma sequência de 5 planos. Veja todos os planos sobre Cálculo mental envolvendo múltiplos de 10
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Andresa Prata Cirino Cuginotti
Mentor: Elisa Greenhalgh Vilalta
Especialista de área: Luciana Tenuta
Habilidades da BNCC
(EF04MA04) Utilizar as relações entre adição e subtração, bem como entre multiplicação e divisão, para ampliar as estratégias de cálculo.
Objetivo específico
Levantar hipóteses, investigar e checar os resultados obtidos na divisão por múltiplos de 10. Utilizar a ideia da divisão como distribuição em partes iguais para descobrir regularidades de divisões por 10 e seus múltiplos. Desenvolver processos de cálculo mental relacionados à divisão.
Conceito-chave
Divisão, cálculo mental.
Vocabulário que será adquirido nesta aula
Múltiplos, decomposição, fatores, divisor, dividendo.
Recursos necessários
- Lápis,
- papel,
- cartolina,
- lápis de cor.
Habilidades BNCC:
Planeje suas aulas pelo Whatsapp!
Qualidade com economia de tempo
Aula
Resumo da aula
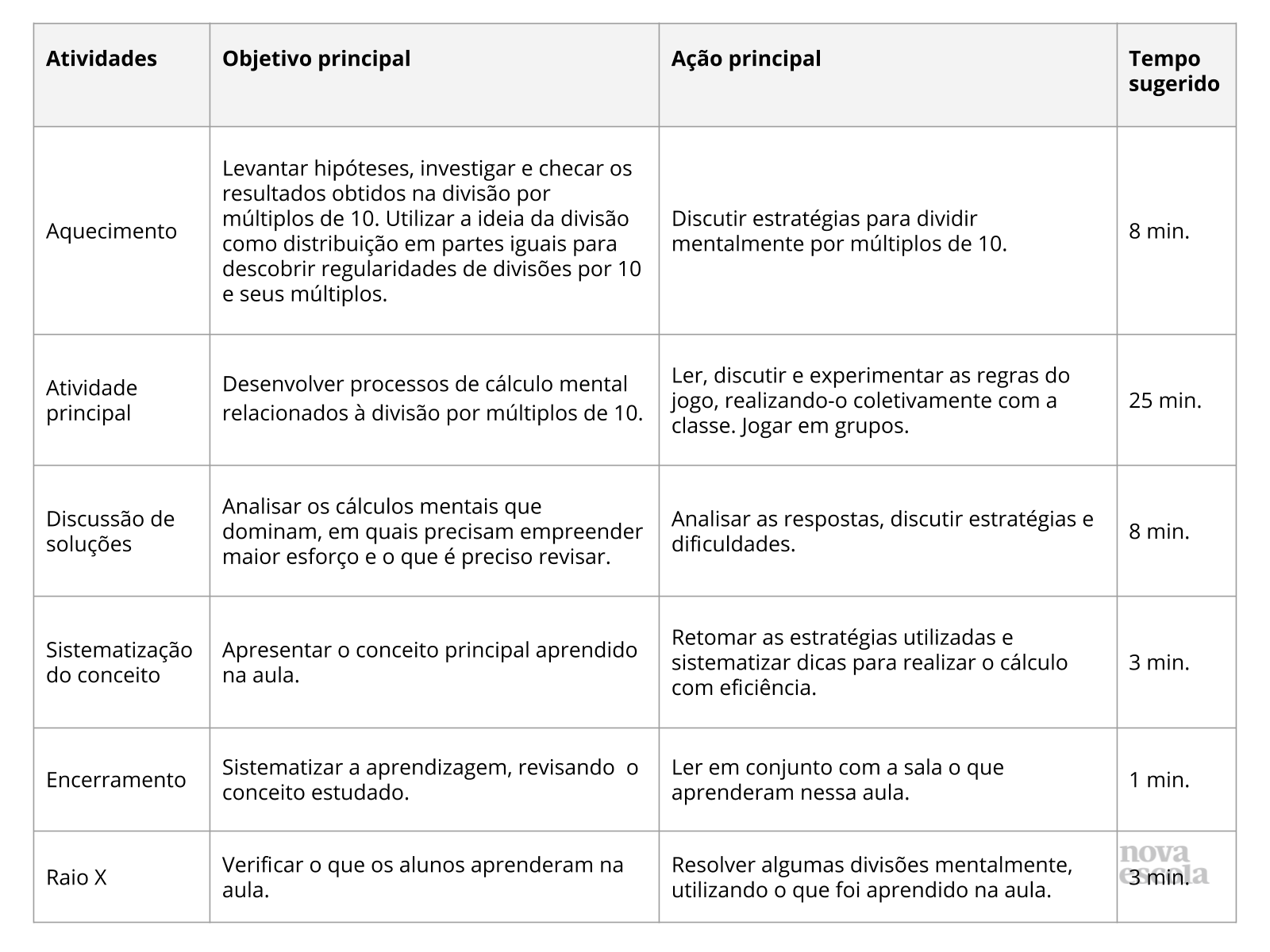 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.












