Atividade Principal
Plano de Aula
Plano de aula: Mínimo múltiplo comum de números naturais
Plano 3 de uma sequência de 7 planos. Veja todos os planos sobre Ampliação dos conceitos de múltiplos e divisores
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Kézia de Oliveira Silva Souza
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
[EF07MA01] Resolver e elaborar problemas envolvendo múltiplos e divisores de um número natural.
Objetivos específicos
- Reconhecer o conceito de múltiplos de números naturais.
- Resolver problemas envolvendo mínimo múltiplo comum de números naturais.
Conceito-chave
Mínimo Múltiplo Comum de números naturais.
Recursos necessários
- Lápis, borracha e caderno;
- Atividades impressas em folhas, coladas no caderno ou não.
Habilidades BNCC:
Objetivos de aprendizagem
- Reconhecer o conceito de múltiplos de números naturais.
- Resolver problemas envolvendo mínimo múltiplo comum de números naturais.
Resumo da aula
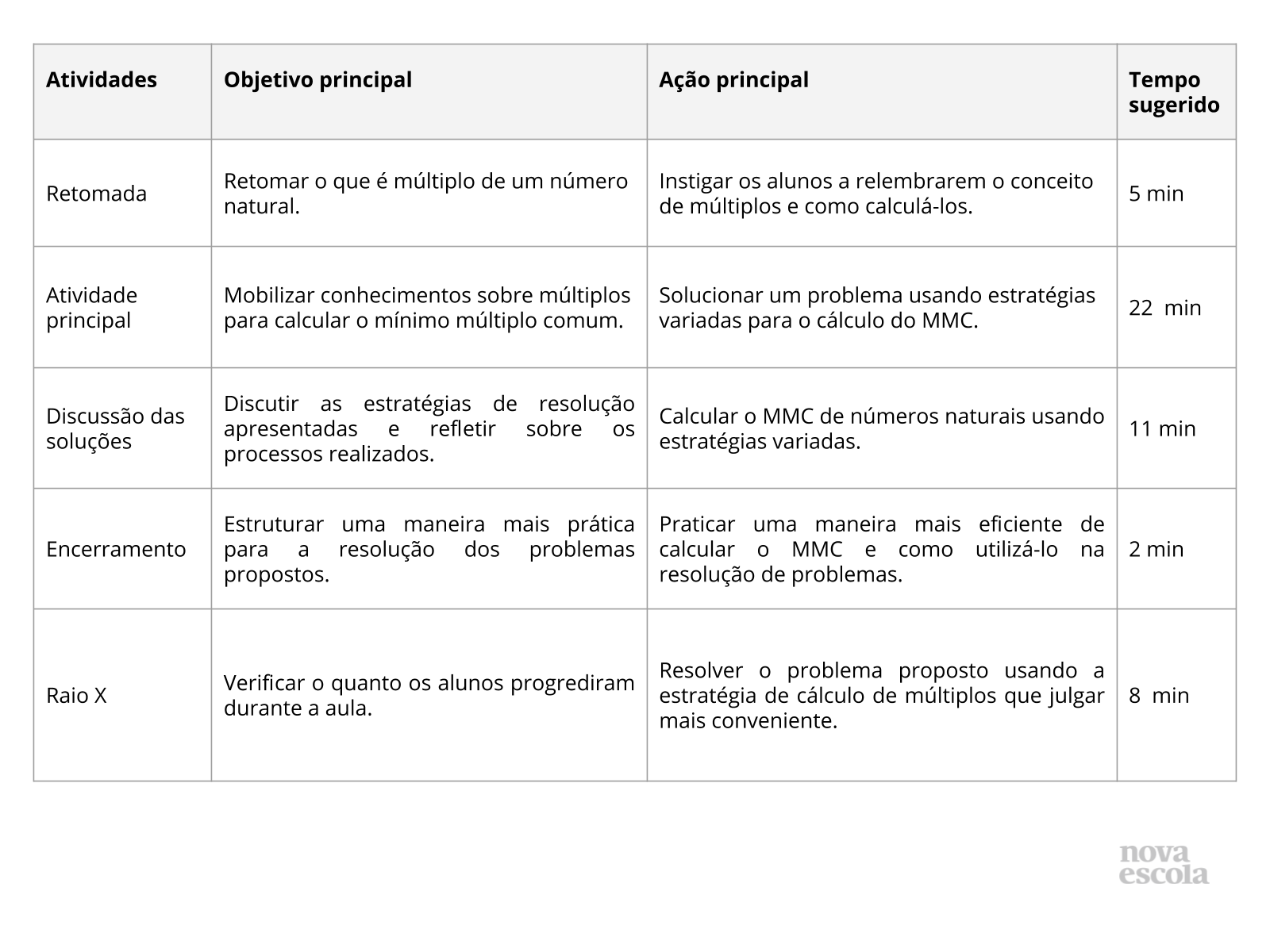
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Sugestão de leitura:
Objetivo
Tempo sugerido: 2 minutos.
Orientação: Projete, escreva no quadro ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento</title
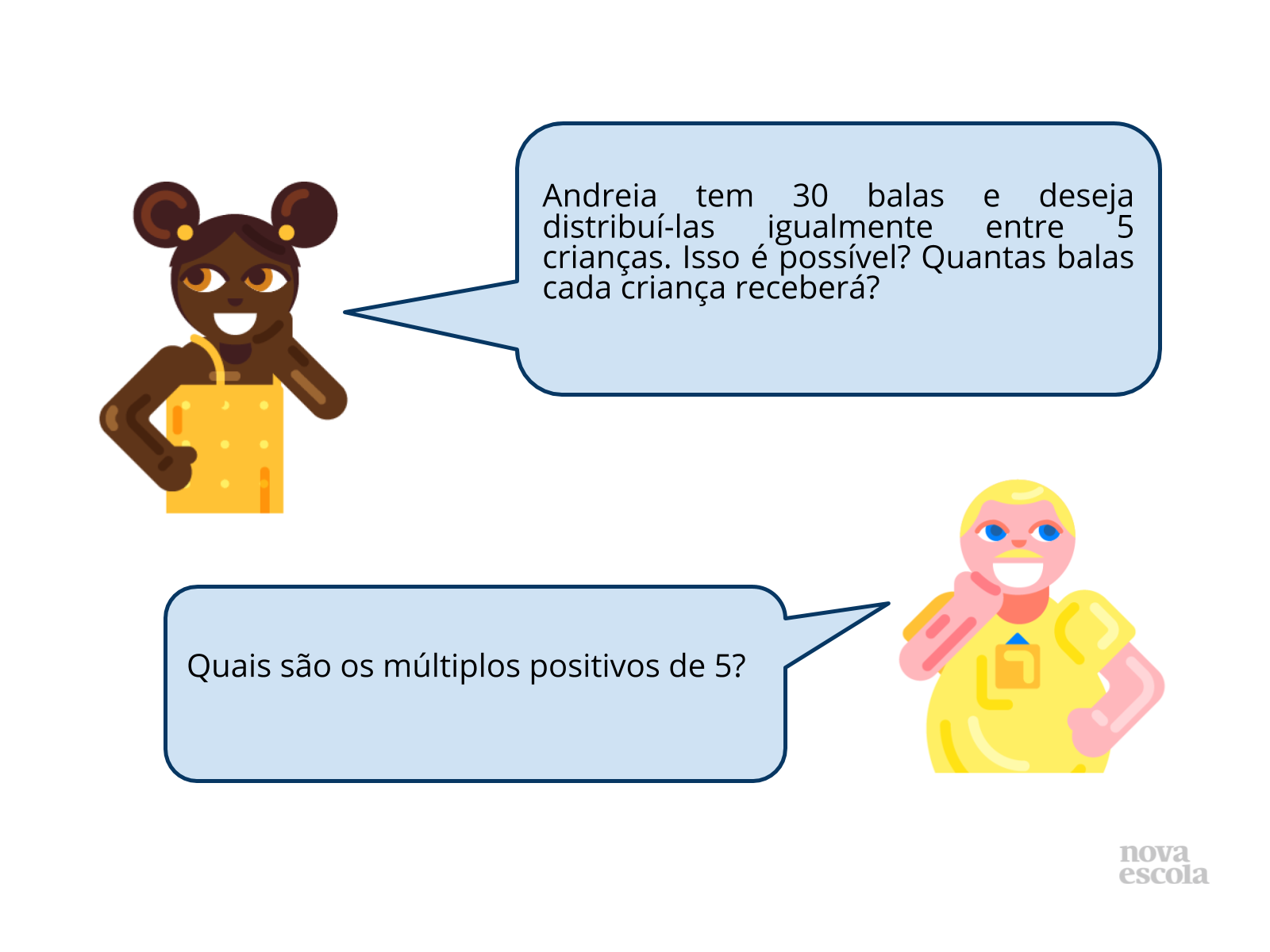 AquecimentoTempo sugerido: 5 minutos.
AquecimentoTempo sugerido: 5 minutos.Orientações: Inicie a aula propondo o problema aos alunos. Espera-se que eles concluam que é possível distribuir de maneira igual 30 balas entre 5 crianças e que cada criança receberá 6 balas. Uma vez que 30:5=6 (trinta dividido por cinco é igual a seis) e 6x5=30 (o produto entre seis e cinco é trinta). Professor, permita que o aluno expresse a maneira como ele calculou, pois ele pode ter somado de cinco em cinco até encontrar trinta, ou até mesmo ter utilizado outra estratégia. Fale com a turma: Como podemos afirmar que cada criança receberá 6 balas?
Após discutir com a turma a situação proposta, pergunte também aos alunos, se eles se lembram o que é múltiplo de um número, qual é a relação entre os múltiplos e divisores e como se calcula o múltiplo de um número. Em seguida, verifique com eles quais são os múltiplos positivos do número 5 (cinco). Observe, professor, que já destacamos apenas os positivos, e por esse motivo o 0 (zero) não deverá ser trabalhado (nulo). A condição de trabalharmos apenas os positivos ajudará a evitar possíveis equívocos por parte dos alunos no cálculo do MMC.
Propósito: Retomar alguns conceitos que serão importantes para o desenvolvimento da atividade.
Discuta com a turma:
- Andreia conseguirá distribuir igualmente as 30 balas para as 5 crianças?
- Trinta é divisível por 5?
- Trinta é múltiplo de 5?
- Cinco é divisor de 30?
- Você se lembra o que é múltiplo de um número?
- Como podemos calcular os múltiplos de um número natural?
- Qual é a relação entre os múltiplos e os divisores?
Atividade principal 1

Tempo sugerido: 15 minutos (Slides 4 a 8)
Orientações: Proponha aos alunos o jogo STOP DOS MÚLTIPLOS COMUNS, uma atividade em que eles resolverão diversas multiplicações e realizarão comparações.
Se possível, imprima a atividade principal com as regras, entregue para os alunos e faça uma leitura compartilhada para tirar as dúvidas. Caso não consiga imprimir para todos, registre no quadro ou em um cartaz que todos consigam ler. Eles podem ainda anotar as regras no caderno para jogar em outras ocasiões com amigos ou mesmo com a família.
Após a leitura das regras, também é possível pedir a um aluno que, voluntariamente, explique para a classe como ele entendeu que se deve realizar a atividade.
Escolha dois alunos voluntários para fazerem uma rodada na lousa para toda a sala ver como acontece. Caso ainda tenham alguma dúvida, este é um bom momento para esclarecê-las. Utilize a grade para exemplificar para os alunos.
Propósito: É esperado que os alunos leiam, discutam e compreendam as regras da atividade proposta e organizem-se para realizá-la.
Discuta com a turma:
- Pergunte aos alunos se eles já jogaram STOP e o que entenderam das regras apresentadas.
- Aproveite para tirar dúvidas e esclarecer possíveis incompreensões.
Material complementar:
- Como jogar Stop: https://pt.wikipedia.org/wiki/Stop!
- Saiba como propor agrupamentos produtivos: https://novaescola.org.br/conteudo/1475/como-agrupo-meus-alunos
- O STOP DOS MÚLTIPLOS COMUNS é uma adaptação do STOP DA MULTIPLICAÇÃO.
Materiais complementares para impressão:
Atividade Principal
Atividade principal 1

Tempo sugerido: 15 minutos (Slides 4 a 8)
Orientações: Proponha aos alunos o jogo STOP DOS MÚLTIPLOS COMUNS, uma atividade em que eles resolverão diversas multiplicações e realizarão comparações.
Se possível, imprima a atividade principal com as regras, entregue para os alunos e faça uma leitura compartilhada para tirar as dúvidas. Caso não consiga imprimir para todos, registre no quadro ou em um cartaz que todos consigam ler. Eles podem ainda anotar as regras no caderno para jogar em outras ocasiões com amigos ou mesmo com a família.
Após a leitura das regras, também é possível pedir a um aluno que, voluntariamente, explique para a classe como ele entendeu que se deve realizar a atividade.
Escolha dois alunos voluntários para fazerem uma rodada na lousa para toda a sala ver como acontece. Caso ainda tenham alguma dúvida, este é um bom momento para esclarecê-las. Utilize a grade para exemplificar para os alunos.
Propósito: É esperado que os alunos leiam, discutam e compreendam as regras da atividade proposta e organizem-se para realizá-la.
Discuta com a turma:
- Pergunte aos alunos se eles já jogaram STOP e o que entenderam das regras apresentadas.
- Aproveite para tirar dúvidas e esclarecer possíveis incompreensões.
Material complementar:
- Como jogar Stop: https://pt.wikipedia.org/wiki/Stop!
- Saiba como propor agrupamentos produtivos: https://novaescola.org.br/conteudo/1475/como-agrupo-meus-alunos
- O STOP DOS MÚLTIPLOS COMUNS é uma adaptação do STOP DA MULTIPLICAÇÃO.
Atividade principal 1

Tempo sugerido: 15 minutos (Slides 4 a 8)
Orientações: Proponha aos alunos o jogo STOP DOS MÚLTIPLOS COMUNS, uma atividade em que eles resolverão diversas multiplicações e realizarão comparações.
Se possível, imprima a atividade principal com as regras, entregue para os alunos e faça uma leitura compartilhada para tirar as dúvidas. Caso não consiga imprimir para todos, registre no quadro ou em um cartaz que todos consigam ler. Eles podem ainda anotar as regras no caderno para jogar em outras ocasiões com amigos ou mesmo com a família.
Após a leitura das regras, também é possível pedir a um aluno que, voluntariamente, explique para a classe como ele entendeu que se deve realizar a atividade.
Escolha dois alunos voluntários para fazerem uma rodada na lousa para toda a sala ver como acontece. Caso ainda tenham alguma dúvida, este é um bom momento para esclarecê-las. Utilize a grade para exemplificar para os alunos.
Propósito: É esperado que os alunos leiam, discutam e compreendam as regras da atividade proposta e organizem-se para realizá-la.
Discuta com a turma:
- Pergunte aos alunos se eles já jogaram STOP e o que entenderam das regras apresentadas.
- Aproveite para tirar dúvidas e esclarecer possíveis incompreensões.
Material complementar:
- Como jogar Stop: https://pt.wikipedia.org/wiki/Stop!
- Saiba como propor agrupamentos produtivos: https://novaescola.org.br/conteudo/1475/como-agrupo-meus-alunos
- O STOP DOS MÚLTIPLOS COMUNS é uma adaptação do STOP DA MULTIPLICAÇÃO.
Atividade principal 1
Tempo sugerido: 15 minutos (Slides 4 a 8)
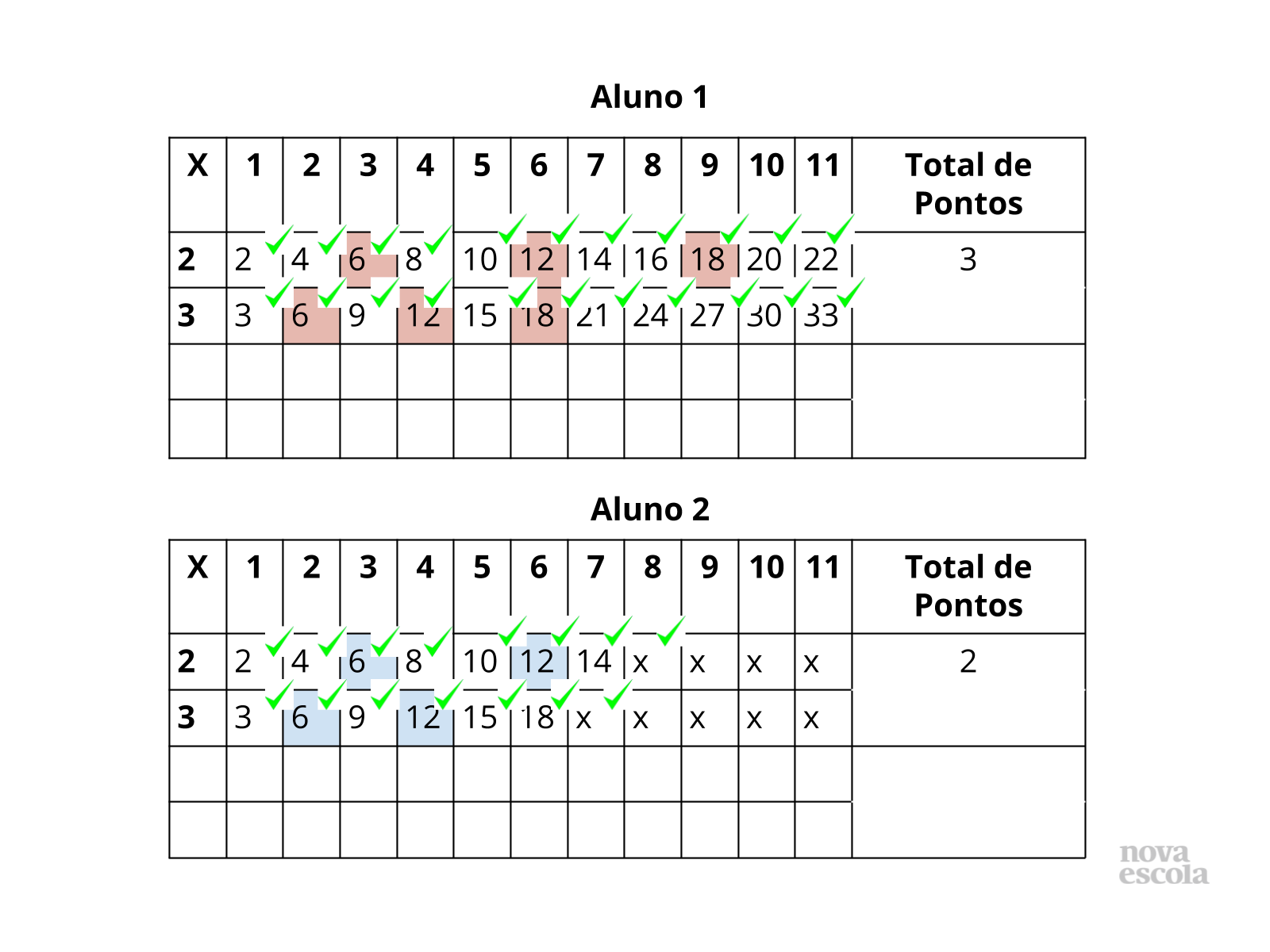
Orientações: Por exemplo, professor, um aluno voluntário escolheu o número 2 e o outro o 3. Assim, cada um deverá preencher uma tabela (grade), o primeiro que concluir as duas linhas deverá falar STOP. É importante que antes de destacar os múltiplos comuns, os alunos verifiquem se todos os produtos estão corretos. Ao verificar e marcar todos os comuns, eles deverão escrever na última coluna o total de pontos. Cada múltiplo comum vale um ponto. Após as três rodadas, vence quem tiver a maior pontuação.
Se todos os alunos tiverem entendido, entregue a cartela da atividade (cópias da cartela ou escreva na lousa) e convide os alunos a desenvolverem a atividade em duplas. A sugestão é que essa atividade seja em duplas, mas ela pode ser realizada em grupos de até 4 (quatro) alunos.
Propósito: Essa atividade tem como intenção que os alunos realizem multiplicações mentalmente, com certa agilidade e encontrar os múltiplos comuns entre dois números naturais diferentes de zero.
Material complementar:
- Como jogar Stop: https://pt.wikipedia.org/wiki/Stop!
- Saiba como propor agrupamentos produtivos: https://novaescola.org.br/conteudo/1475/como-agrupo-meus-alunos
- O STOP DOS MÚLTIPLOS COMUNS é uma adaptação do STOP DA MULTIPLICAÇÃO.
Atividade principal 1
Tempo sugerido: 15 minutos (Slides 4 a 8)
Orientações: Por exemplo, professor, um aluno voluntário escolheu o número 2 e o outro o 3. Assim, cada um deverá preencher uma tabela (grade), o primeiro que concluir as duas linhas deverá falar STOP. É importante que antes de destacar os múltiplos comuns, os alunos verifiquem se todos os produtos estão corretos. Ao verificar e marcar todos os comuns, eles deverão escrever na última coluna o total de pontos. Cada múltiplo comum vale um ponto. Após as três rodadas, vence quem tiver a maior pontuação.
Se todos os alunos tiverem entendido, entregue a cartela da atividade (cópias da cartela ou escreva na lousa) e convide os alunos a desenvolverem a atividade em duplas. A sugestão é que essa atividade seja em duplas, mas ela pode ser realizada em grupos de até 4 (quatro) alunos.
Propósito: Essa atividade tem como intenção que os alunos realizem multiplicações mentalmente, com certa agilidade e encontrar os múltiplos comuns entre dois números naturais diferentes de zero.
Material complementar:
- Como jogar Stop: https://pt.wikipedia.org/wiki/Stop!
- Saiba como propor agrupamentos produtivos: https://novaescola.org.br/conteudo/1475/como-agrupo-meus-alunos
- O STOP DOS MÚLTIPLOS COMUNS é uma adaptação do STOP DA MULTIPLICAÇÃO.
Discussão de soluções
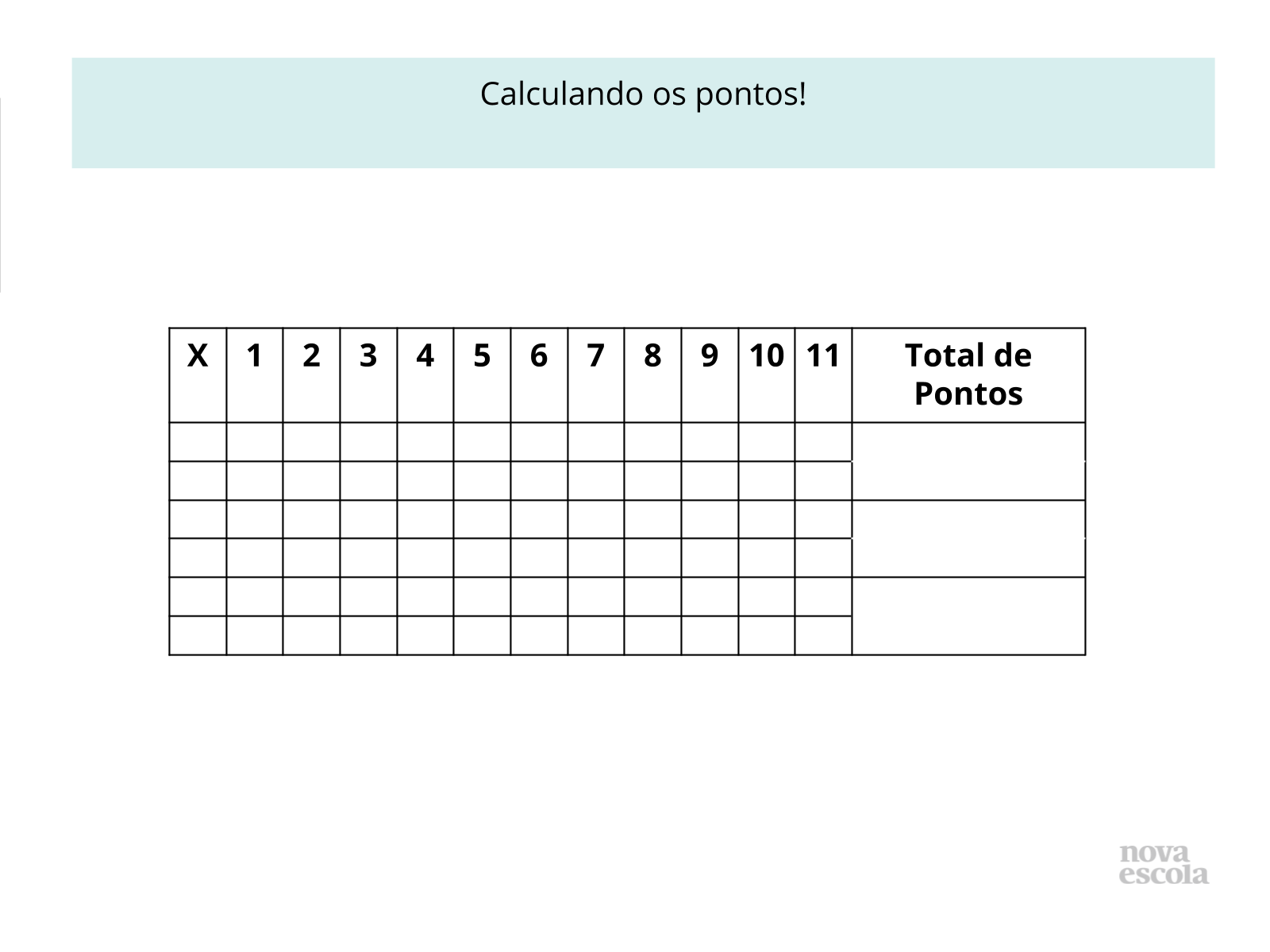
Tempo sugerido: 4 minutos.
Orientações: Peça aos alunos que observem individualmente suas cartelas e analisem seu desempenho. Projete ou reproduza no quadro a cartela completa da atividade com todos os possíveis fatores escolhidos por eles e os auxilie de acordo com a escolha da dupla para verificar quais são os múltiplos comuns.
Propósito: Ao realizar esse processo desejamos incentivar a agilidade dos alunos ao resolver as atividades e também levá-los a perceber que o cálculo do mínimo múltiplo comum é bem simples, mas pode se tornar algo trabalhoso se o múltiplo comum não estiver entre os primeiros múltiplos.
Discuta com a turma:
- Quais multiplicações você errou? Que tipo de erro cometeu?
- A agilidade na resolução é importante?
- Escreva algumas dicas pessoais para melhorar seu desempenho para uma próxima vez que for realizar essa atividade.
- É possível descobrir o menor múltiplo comum de dois números sem escrever os seus múltiplos?
Atividade principal 2

Tempo sugerido: 7 minutos.
Orientações: Professor, você poderá escrever o texto do problema no quadro, projetá-lo ou entregar uma cópia aos alunos. Comece perguntando aos alunos o que eles entenderam do enunciado, peça que alguém conte o que o problema está abordando, pergunte se tem alguma palavra desconhecida no enunciado. Atenção, professor! Esse momento é para o aluno entender, interpretar o enunciado e não é para a resolução oral, pois, ele precisará traçar a sua própria estratégia de resolução.
Deixe que os alunos leiam o problema novamente e dê tempo para que tentem resolvê-lo de forma individual. Após esse momento inicial de resolução, proponha que discutam as resoluções juntamente com um colega, verificando se ambos chegaram à mesma conclusão e se usaram as mesmas estratégias. Incentive-os a usar outras estratégias de resolução e também a verificar se a resposta está correta.
Não faça nenhuma intervenção neste momento, observe como os alunos analisam os dados do problema, interpretam e elaboram suas estratégias.
Propósito: Fazer com que os alunos mobilizem os conhecimentos que já possuem de múltiplos para tentar solucionar o problema dado.
Discuta com a turma:
- Quantos bombons são colocados na caixa de bombons recheados de licor?
- Se a cliente comprar duas caixas de bombons recheados de licor, quantos bombons ela terá? E se forem três caixas? E quatro?
- Quantos bombons são colocados na caixa de bombons recheados de fruta?
- Se a cliente comprar duas caixas de bombons recheados de fruta, quantos bombons ela terá? E se forem três caixas? E quatro?
Materiais complementares para impressão:
Discussão de soluções
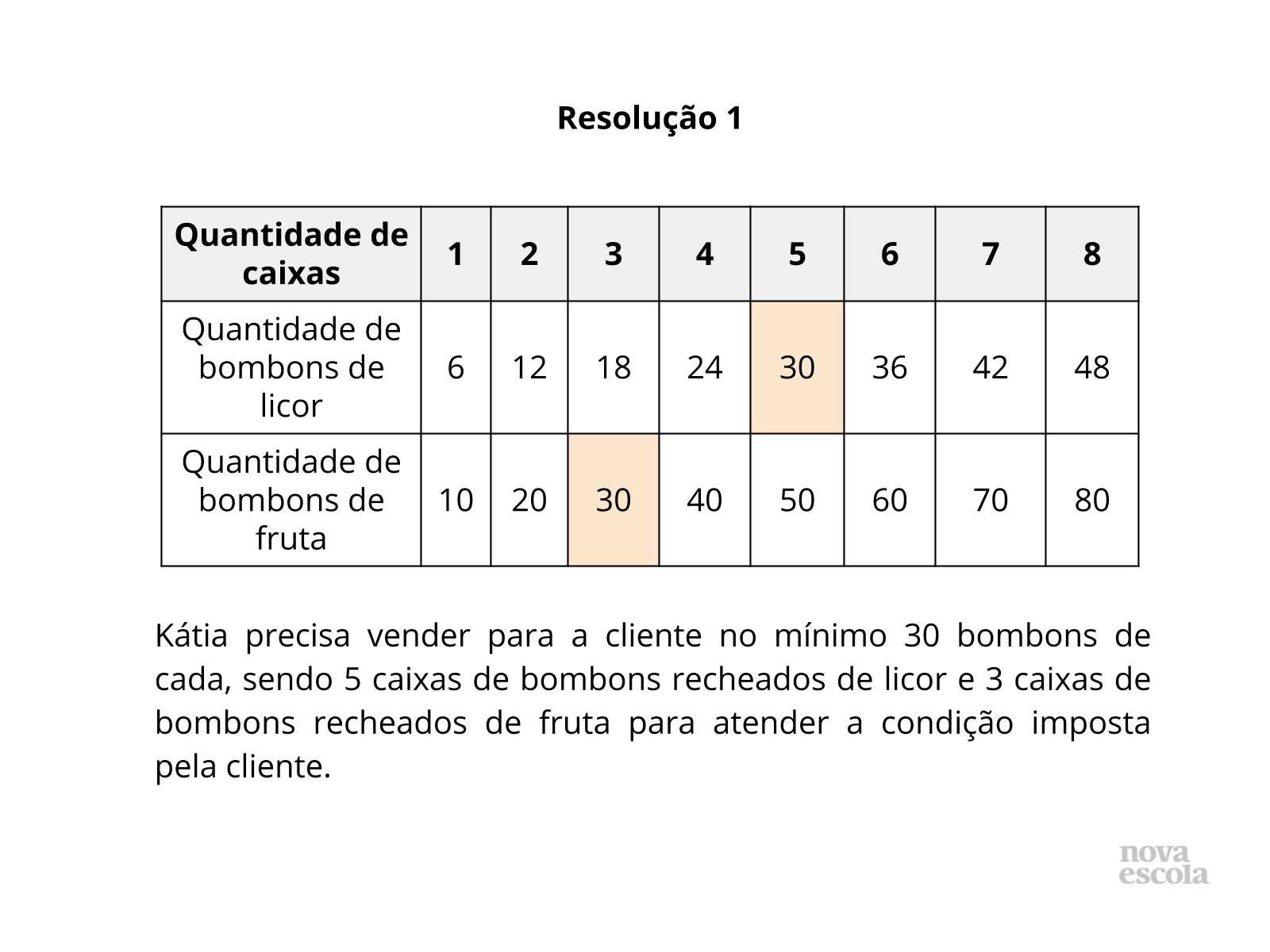
Tempo sugerido: 7 minutos. (Slides 11 a 13)
Orientações: Peça que três alunos apresentem as resoluções para as outras crianças e expliquem como resolveram a situação proposta. Caso algum aluno da turma tenha proposto uma explicação diferente, peça que vá até o quadro e a explique para os colegas.
Propósito: Incentivar que os alunos tentem explicar o raciocínio utilizado para solucionar uma questão. Espera-se que os estudantes sejam capazes de refletir se uma estratégia é mais eficiente que a outra na situação-problema apresentada.
Na resolução 1, o aluno criou uma tabela. Para calcular a quantidade de bombons, o aluno somou 6 bombons (no caso do sabor “licor”) ou 10 bombons (no caso do sabor “fruta”) à quantidade anterior, por exemplo: 6+6=12 bombons, mais uma caixa: 12+6=18, e assim sucessivamente. Completou a tabela e verificou que 30 bombons são suficientes.
Materiais complementares para impressão:
Discussão de soluções
Tempo sugerido: 7 minutos. (Slides 11 a 13)
Orientações: Peça que três alunos apresentem as resoluções para as outras crianças e expliquem como resolveram a situação proposta. Caso algum aluno da turma tenha proposto uma explicação diferente, peça que vá até o quadro e a explique para os colegas.
Propósito: Incentivar que os alunos tentem explicar o raciocínio utilizado para solucionar uma questão. Espera-se que os estudantes sejam capazes de refletir se uma estratégia é mais eficiente que a outra na situação-problema apresentada.
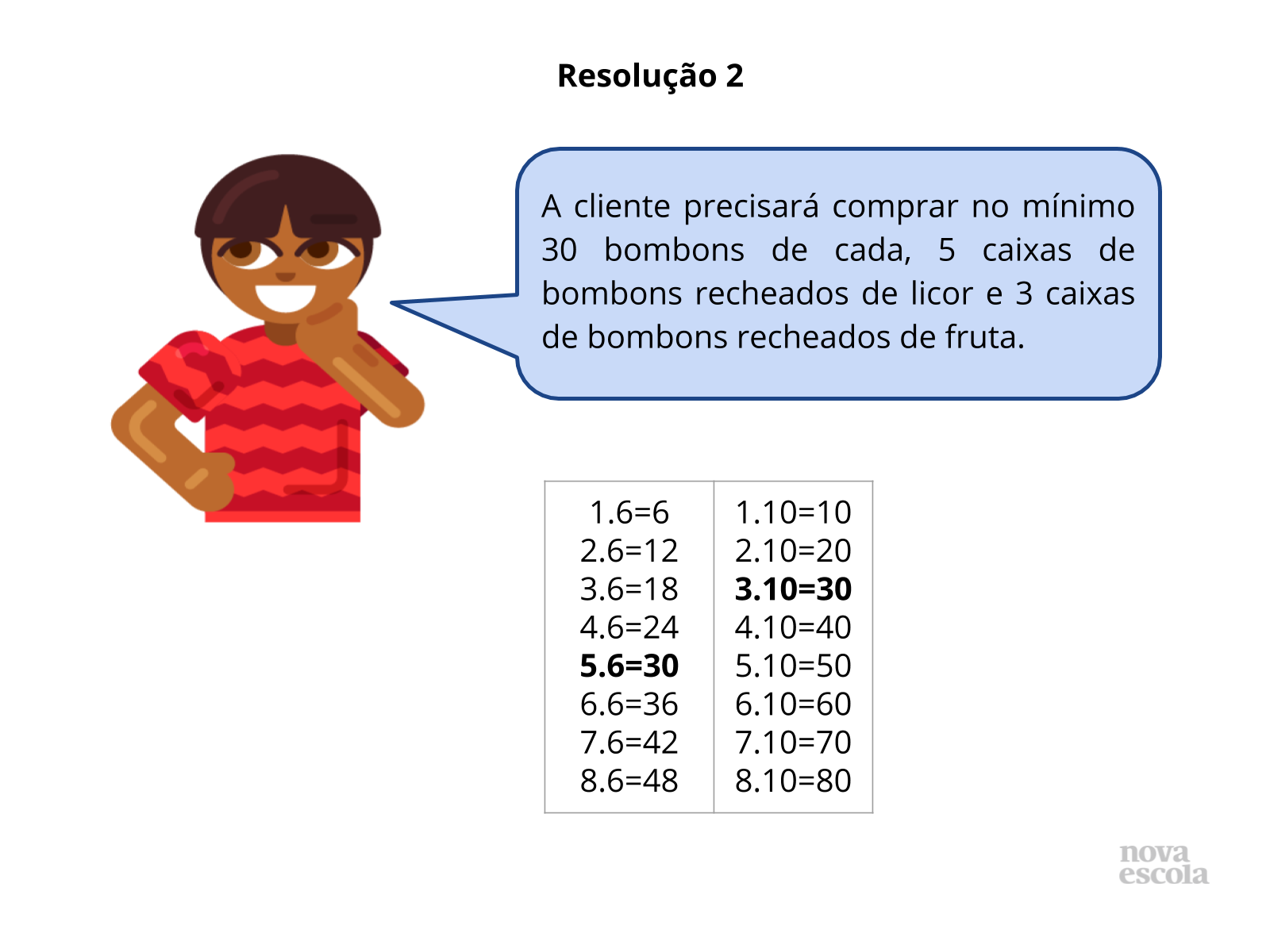
Na resolução 2, o aluno realizou um raciocínio parecido com o do aluno da resolução 1, mas ao invés de usar a adição, ele usou a multiplicação.
Materiais complementares para impressão:
Discussão de soluções
Tempo sugerido: 7 minutos. (Slides 11 a 13)
Orientações: Peça que três alunos apresentem as resoluções para as outras crianças e expliquem como resolveram a situação proposta. Caso algum aluno da turma tenha proposto uma explicação diferente, peça que vá até o quadro e a explique para os colegas.
Propósito: Incentivar que os alunos tentem explicar o raciocínio utilizado para solucionar uma questão. Espera-se que os estudantes sejam capazes de refletir se uma estratégia é mais eficiente que a outra na situação-problema apresentada.
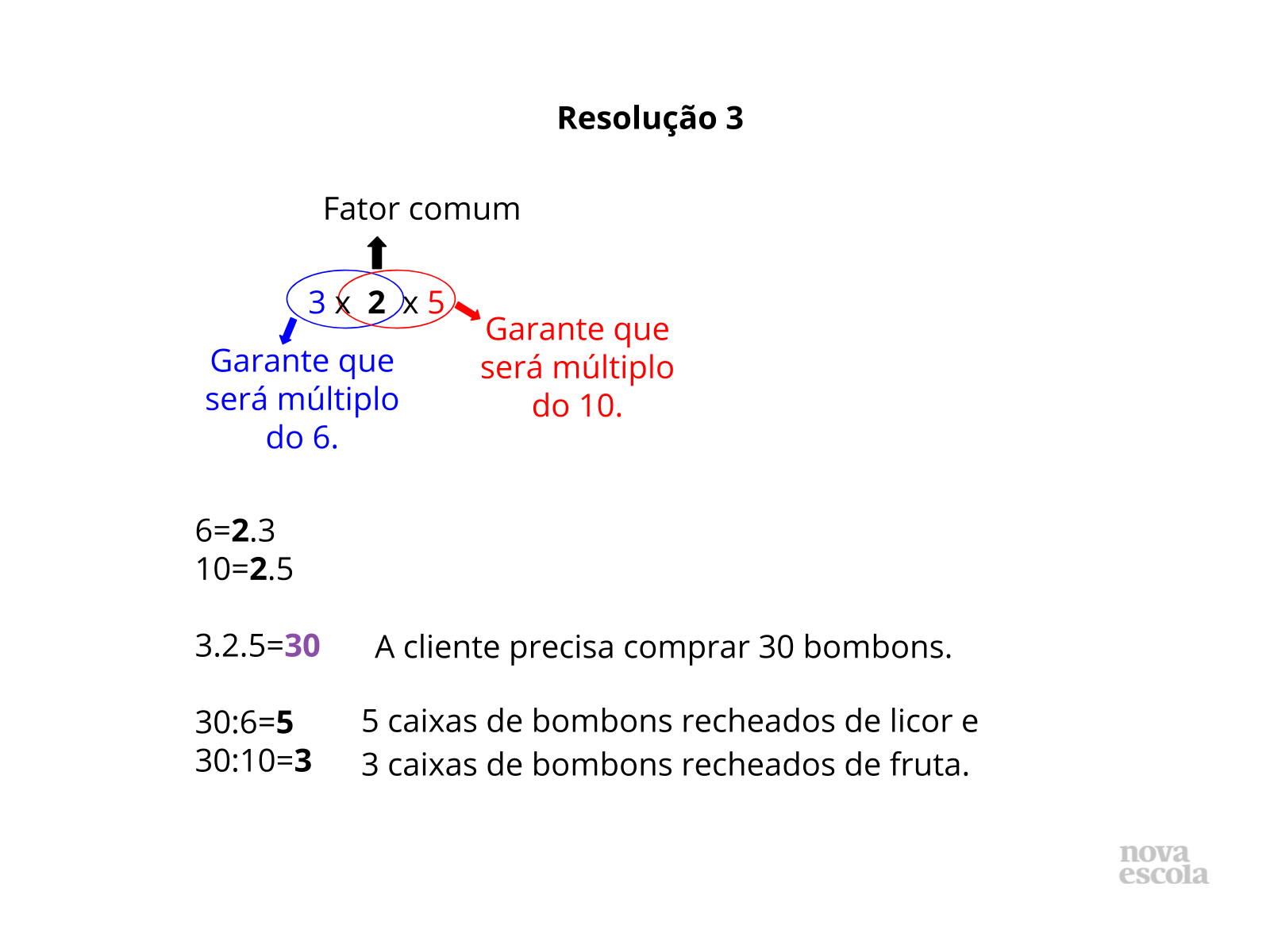
Na resolução 3, o aluno escreveu os dois números em fatores primos. Assim, ele verificou qual era o fator comum, para não repetir e multiplicou os fatores não comuns com o fator comum.
Materiais complementares para impressão:
Encerramento

Tempo sugerido: 2 minutos.
Orientação: Feche a atividade lendo ou deixando que os alunos leiam a aprendizagem da aula e destaque que problemas como a atividade 2 são solucionadas por meio do MMC. Se desejar, anote a frase no quadro ou num cartaz para deixar exposto em sala de aula.
Raio x

Tempo sugerido: 8 minutos.
Orientações: Apresente o problema e peça que os alunos o resolvam individualmente. Em seguida, eles devem socializar as respostas com os outros alunos da turma. Você pode projetar, passar no quadro ou fazer cópia para os alunos. O raio x é um momento para você avaliar se todos os alunos conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um.
Propósito: O aluno precisa relembrar o que são múltiplos, interpretar o enunciado e reconhecer quais são os comuns.
Discuta com a turma:
- Como podemos representar os dias que as netas visitarão a avó?
- Quais são os dias de janeiro em que Clara visitará a avó?
- Quais são os dias de janeiro em que Fernanda visitará a avó?
- Em quais dias as duas visitaram juntas a avó?
Materiais complementares para impressão:
Para os Alunos
Para o Professor
Sugestão de adaptação para ensino remoto
Recursos
Necessários:
- Lápis;
- Caderno;
- Aplicativo Zoom.
Opcionais:
- Podcast (para saber mais sobre a ferramenta, veja o vídeo disponível aqui).
Para este plano, foque na etapa Atividade Principal.
Aquecimento
A atividade é uma retomada de conceitos fundamentais para a aula. Você pode propor os questionamentos apresentados no slide usando um editor de texto (Google Docs, por exemplo) em que, de maneira colaborativa e síncrona, os alunos possam respondê-los, usar a função de áudio do Whatsapp para que um a um postem as respostas ou hipóteses sobre o assunto disparador. Oriente-os explicando que esse é um momento de retomada de conteúdos e que, caso tenham dúvidas, elas serão trabalhadas no decorrer da aula.
Atividade principal
A atividade principal consiste em um jogo. Proponha aos alunos o jogo STOP DOS MÚLTIPLOS COMUNS. Nesta atividade, eles resolverão diversas multiplicações e realizarão comparações. Combine previamente o jogo com a turma e, usando um Podcast ou o recurso de áudio do Whatsapp, explique as regras e oriente-os a reproduzirem no caderno a tabela para o jogo. No dia marcado, usando o recurso do aplicativo Zoom, divida os alunos em Breakout Rooms (salas para grupos menores dentro da chamada de vídeo) para que possam jogar em duplas.
Para saber mais sobre o Zoom: Pocket-lint (disponível aqui).
Discussão das soluções
A discussão das soluções da atividade é uma etapa importantíssima da aula. Retorne para a sala principal do Zoom e converse com os alunos sobre a atividade. Neste moment,o estimule a turma a falar como pensou para resolver o problema.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para os alunos. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa.
Portanto, indicamos que sugira aos alunos que, em um momento de descontração, joguem novamente o jogo da atividade principal com as famílias .
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Kézia de Oliveira Silva Souza
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
[EF07MA01] Resolver e elaborar problemas envolvendo múltiplos e divisores de um número natural.
Objetivos específicos
- Reconhecer o conceito de múltiplos de números naturais.
- Resolver problemas envolvendo mínimo múltiplo comum de números naturais.
Conceito-chave
Mínimo Múltiplo Comum de números naturais.
Recursos necessários
- Lápis, borracha e caderno;
- Atividades impressas em folhas, coladas no caderno ou não.