Atividade principal
Plano de Aula
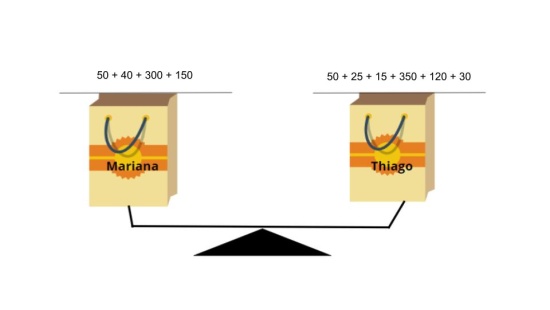
Plano de aula: Equivalência com frutas na balança
Plano 6 de uma sequência de 10 planos. Veja todos os planos sobre Sentido de igualdade em operação numérica
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor/Mentor: Paulo César da Silva Rocha
Revisora Pedagógica: Eliane Zanin
Especialista de área: Sandra Regina Correa Amorim
Habilidade da BNCC
(EF03MA11) Compreender a ideia de igualdade para escrever diferentes sentenças de adições ou de subtrações de dois números naturais que resultem na mesma soma ou diferença.
Objetivos específicos
Interpretar e exemplificar uma equivalência
Conceito-chave
Igualdade e equivalência
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não;
- Datashow ( opcional ).
Habilidades BNCC:
Objetivos de aprendizagem
Interpretar e exemplificar uma equivalência

Precisa de ajuda para criar uma aula personalizada?
Crie seu plano de aula em menos de um minuto no WhatsApp.
Aula
Resumo da aula
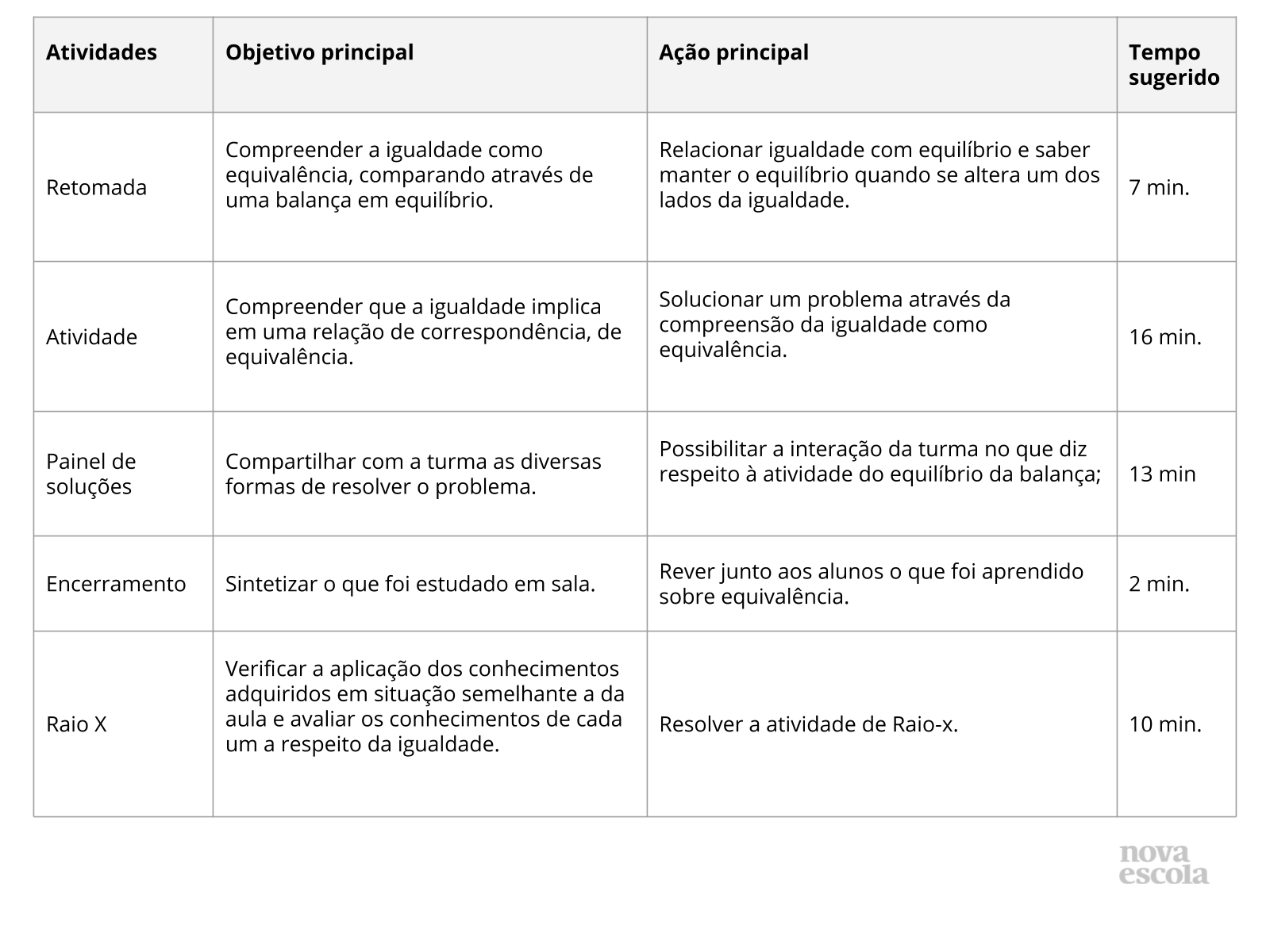
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Projete ou leia o objetivo para os alunos.
Propósito: Compartilhe o objetivo da aula com a turma.
Um novo aliado para Professores Alfabetizadores

Acompanhe o progresso dos alunos durante o ano e otimize seu planejamento
ACESSAR AGORA