Aquecimento
Plano de Aula
Plano de aula: Simetria nos triângulos e quadriláteros e a congruência de triângulos
Plano 9 de uma sequência de 10 planos. Veja todos os planos sobre Transformações isométricas e congruência de triângulos
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Renata Akemi Maekawa
Mentor: Fabricio Eduardo Ferreira
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
EF08MA12 - Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
EF08MA15 - Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.
Objetivos específicos
-Reconhecer e traçar eixos de simetria de figuras
-Utilizar critérios de congruência de triângulos para justificar que uma reta é um eixo de simetria.
-Relacionar as classificações dos triângulos quanto aos lados ao número de eixos de simetria que a figura possui.
Conceito-chave
Simetrias e congruência de triângulos.
Recursos necessários
-Fichas impressas.
-Projetor (se possível)
Habilidades BNCC:
Objetivos de aprendizagem
-Reconhecer e traçar eixos de simetria de figuras
-Utilizar critérios de congruência de triângulos para justificar que uma reta é um eixo de simetria.
-Relacionar as classificações dos triângulos quanto aos lados ao número de eixos de simetria que a figura possui.
Resumo da aula
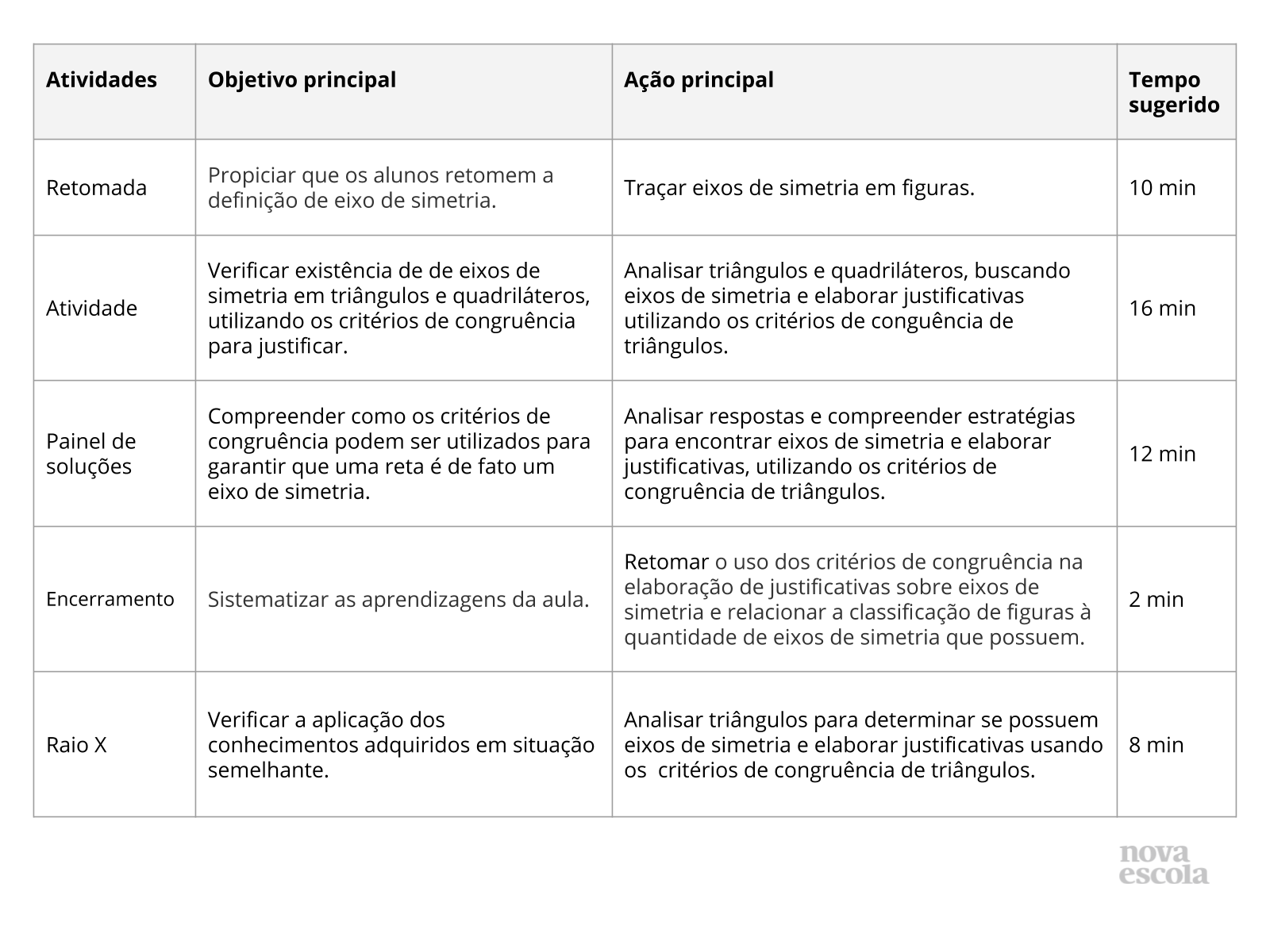
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo sugerido: 10 minutos (slides 3 a 6).
Orientações: Projete o slide 3 ou escreva a pergunta na lousa e leia para os alunos. Abra para que os alunos participem para retomar a definição de eixo de simetria. Sugira que os alunos façam imagens na lousa para ilustrar essa definição. Em seguida, projete e leia o texto do slide 4 para formalizar esta retomada e fornecer mais algumas imagens que ajudam a ilustrar a existência de eixos de simetria em figuras.
Em seguida, projete a atividade do slide 5 (se possível) e entregue cópias da atividade para os alunos. Solicite que os alunos resolvam individualmente usando régua para traçar os eixos. Depois, abra para que os alunos compartilhem suas resoluções. É importante que os alunos expliquem para a sala por que as retas que traçaram representam eixos de simetria das figuras e que verifiquem se traçaram todos os eixos de simetria que as figuras possuem.
Por fim, se considerar necessário e se o recurso da projeção estiver disponível, utilize o slide 6 para formalizar a resolução da atividade.
Propósito: Propiciar que os alunos retomem a definição de eixo de simetria de figuras planas.
Discuta com a turma:
- É possível traçar mais eixos de simetria na joaninha? E na chave de boca?
- Por que a mão não possui eixos de simetria?
- Como podemos garantir que uma reta é um eixo de simetria de uma figura?
Materiais complementares para impressão:
Retomada
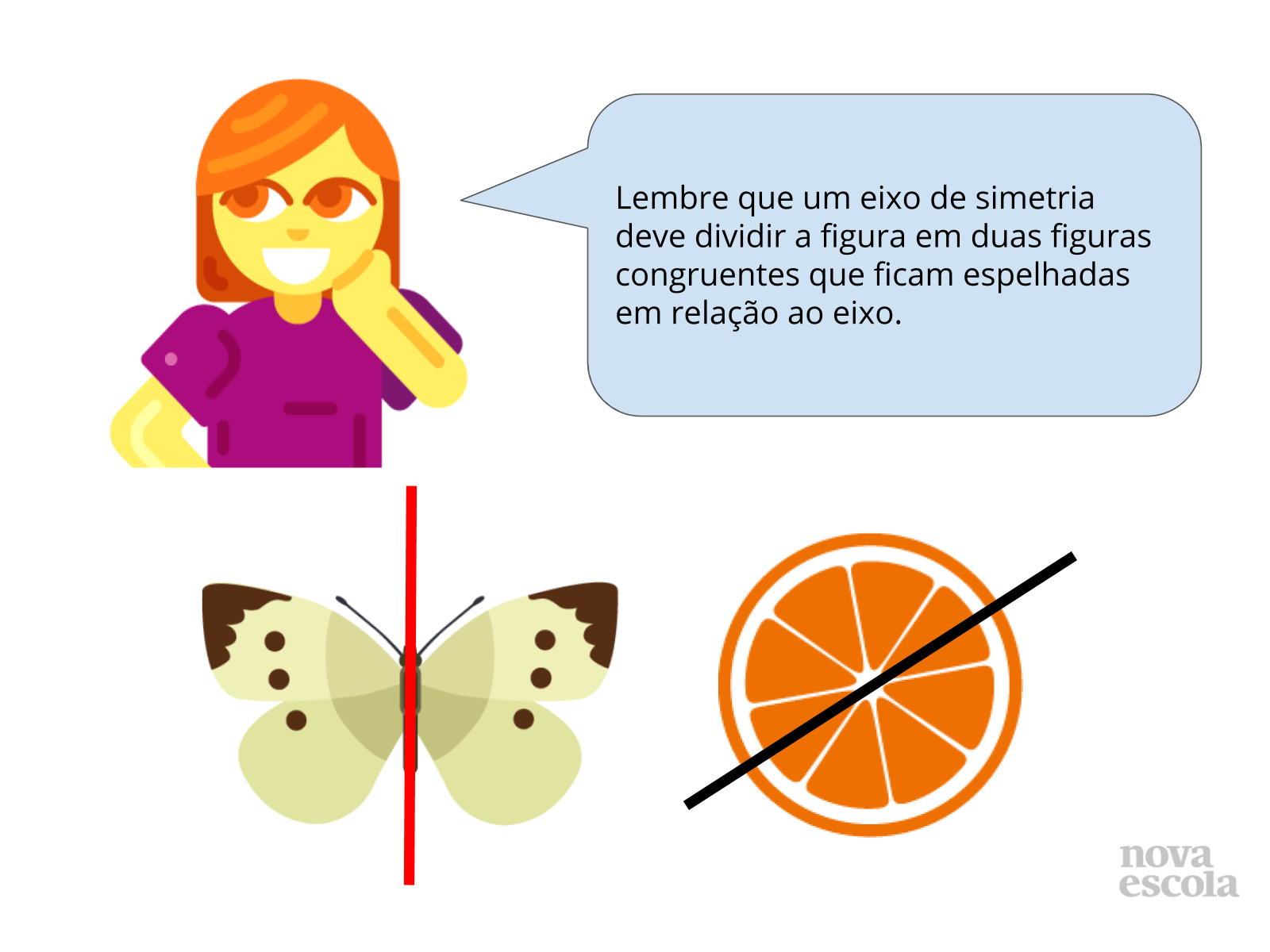
Tempo sugerido: 10 minutos (slides 3 a 6).
Orientações: Projete o slide 3 ou escreva a pergunta na lousa e leia para os alunos. Abra para que os alunos participem para retomar a definição de eixo de simetria. Sugira que os alunos façam imagens na lousa para ilustrar essa definição. Em seguida, projete e leia o texto do slide 4 para formalizar esta retomada e fornecer mais algumas imagens que ajudam a ilustrar a existência de eixos de simetria em figuras.
Em seguida, projete a atividade do slide 5 (se possível) e entregue cópias da atividade para os alunos. Solicite que os alunos resolvam individualmente usando régua para traçar os eixos. Depois, abra para que os alunos compartilhem suas resoluções. É importante que os alunos expliquem para a sala por que as retas que traçaram representam eixos de simetria das figuras e que verifiquem se traçaram todos os eixos de simetria que as figuras possuem.
Por fim, se considerar necessário e se o recurso da projeção estiver disponível, utilize o slide 6 para formalizar a resolução da atividade.
Propósito: Propiciar que os alunos retomem a definição de eixo de simetria de figuras planas.
Discuta com a turma:
- É possível traçar mais eixos de simetria na joaninha? E na chave de boca?
- Por que a mão não possui eixos de simetria?
- Como podemos garantir que uma reta é um eixo de simetria de uma figura?
Material complementar: a presença de simetrias na natureza e no corpo humano pode ser um tema interessante para ser pesquisado e explorado pelos estudantes (links para alguns sites: link 1, link 2, link 3, link 4, link 5, link 6).
Retomada

Tempo sugerido: 10 minutos (slides 3 a 6).
Orientações: Projete o slide 3 ou escreva a pergunta na lousa e leia para os alunos. Abra para que os alunos participem para retomar a definição de eixo de simetria. Sugira que os alunos façam imagens na lousa para ilustrar essa definição. Em seguida, projete e leia o texto do slide 4 para formalizar esta retomada e fornecer mais algumas imagens que ajudam a ilustrar a existência de eixos de simetria em figuras.
Em seguida, projete a atividade do slide 5 (se possível) e entregue cópias da atividade para os alunos. Solicite que os alunos resolvam individualmente usando régua para traçar os eixos. Depois, abra para que os alunos compartilhem suas resoluções. É importante que os alunos expliquem para a sala por que as retas que traçaram representam eixos de simetria das figuras e que verifiquem se traçaram todos os eixos de simetria que as figuras possuem.
Por fim, se considerar necessário e se o recurso da projeção estiver disponível, utilize o slide 6 para formalizar a resolução da atividade.
Propósito: Propiciar que os alunos retomem a definição de eixo de simetria de figuras planas.
Discuta com a turma:
- É possível traçar mais eixos de simetria na joaninha? E na chave de boca?
- Por que a mão não possui eixos de simetria?
- Como podemos garantir que uma reta é um eixo de simetria de uma figura?
Material complementar: a presença de simetrias na natureza e no corpo humano pode ser um tema interessante para ser pesquisado e explorado pelos estudantes (links para alguns sites: link 1, link 2, link 3, link 4, link 5, link 6). No guia de intervenções você pode encontrar mais detalhes sobre essa proposta.
Retomada
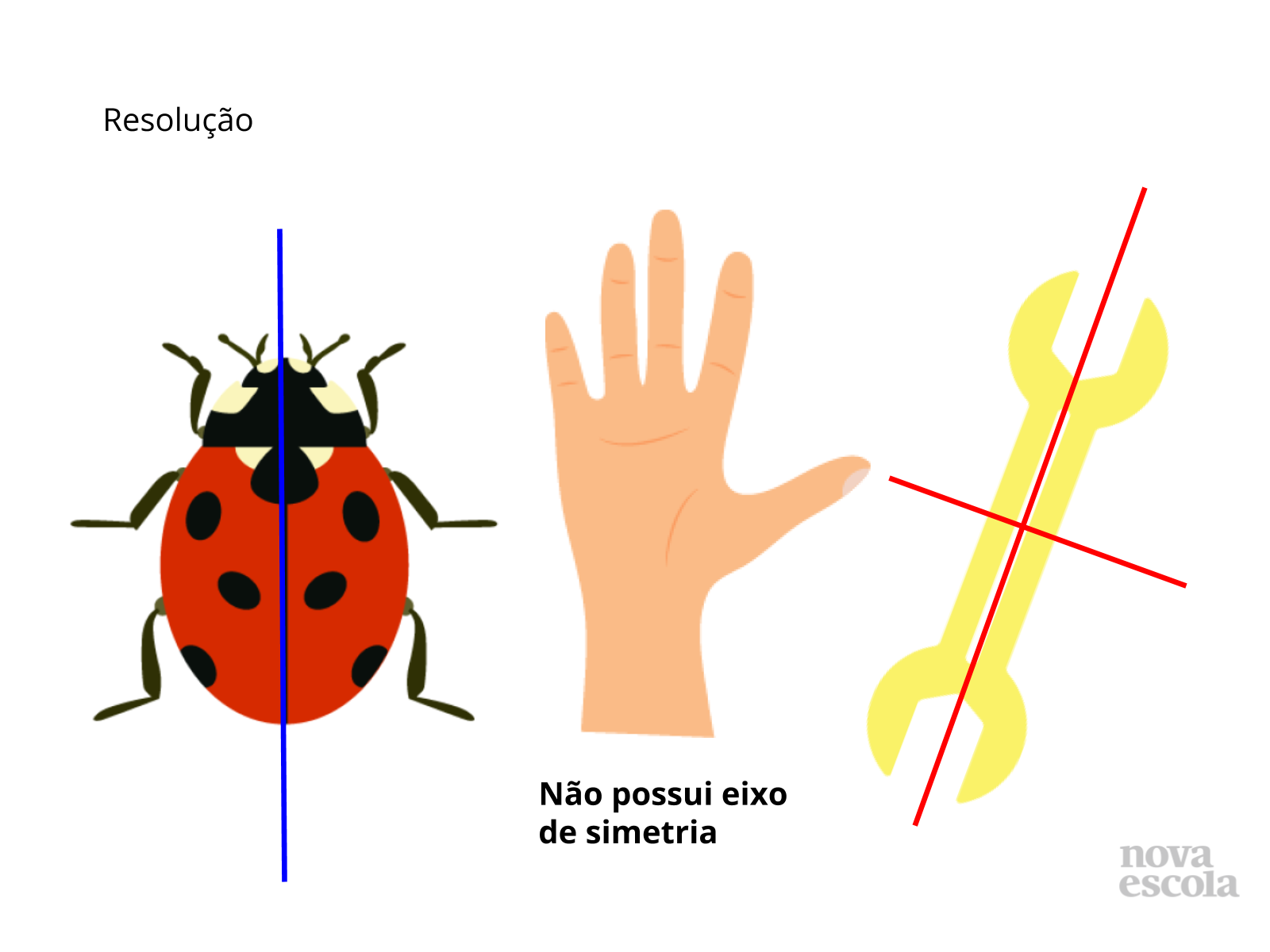
Tempo sugerido: 10 minutos (slides 3 a 6).
Orientações: Projete o slide 3 ou escreva a pergunta na lousa e leia para os alunos. Abra para que os alunos participem para retomar a definição de eixo de simetria. Sugira que os alunos façam imagens na lousa para ilustrar essa definição. Em seguida, projete e leia o texto do slide 4 para formalizar esta retomada e fornecer mais algumas imagens que ajudam a ilustrar a existência de eixos de simetria em figuras.
Em seguida, projete a atividade do slide 5 (se possível) e entregue cópias da atividade para os alunos. Solicite que os alunos resolvam individualmente usando régua para traçar os eixos. Depois, abra para que os alunos compartilhem suas resoluções. É importante que os alunos expliquem para a sala por que as retas que traçaram representam eixos de simetria das figuras e que verifiquem se traçaram todos os eixos de simetria que as figuras possuem.
Por fim, se considerar necessário e se o recurso da projeção estiver disponível, utilize o slide 6 para formalizar a resolução da atividade.
Propósito: Propiciar que os alunos retomem a definição de eixo de simetria de figuras planas.
Discuta com a turma:
- É possível traçar mais eixos de simetria na joaninha? E na chave de boca?
- Por que a mão não possui eixos de simetria?
- Como podemos garantir que uma reta é um eixo de simetria de uma figura?
Material complementar: a presença de simetrias na natureza e no corpo humano pode ser um tema interessante para ser pesquisado e explorado pelos estudantes (links para alguns sites: link 1, link 2, link 3, link 4, link 5, link 6). No guia de intervenções você pode encontrar mais detalhes sobre essa proposta.
Atividade principal
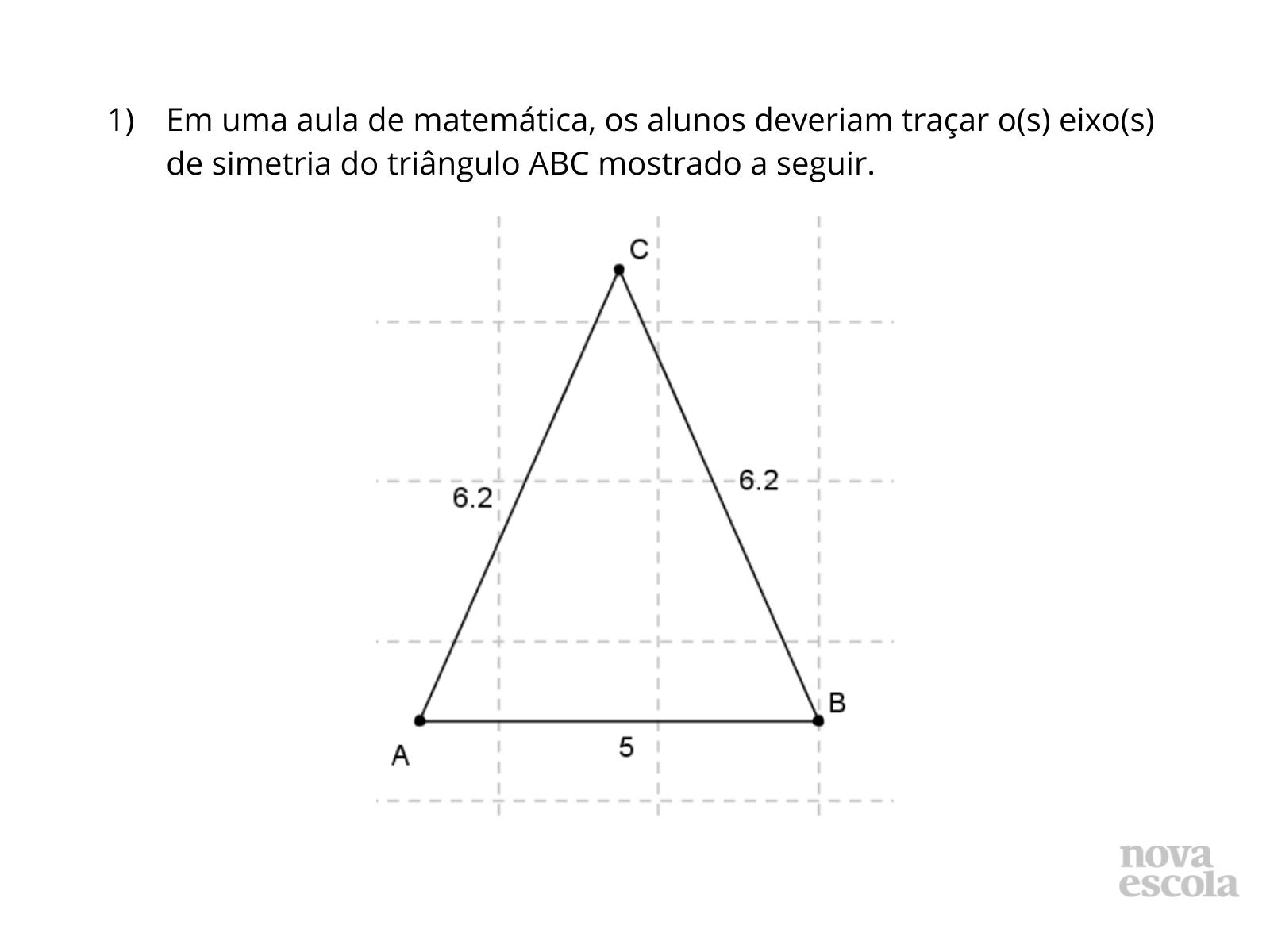
Tempo sugerido: 8 minutos (slides 7 a 9).
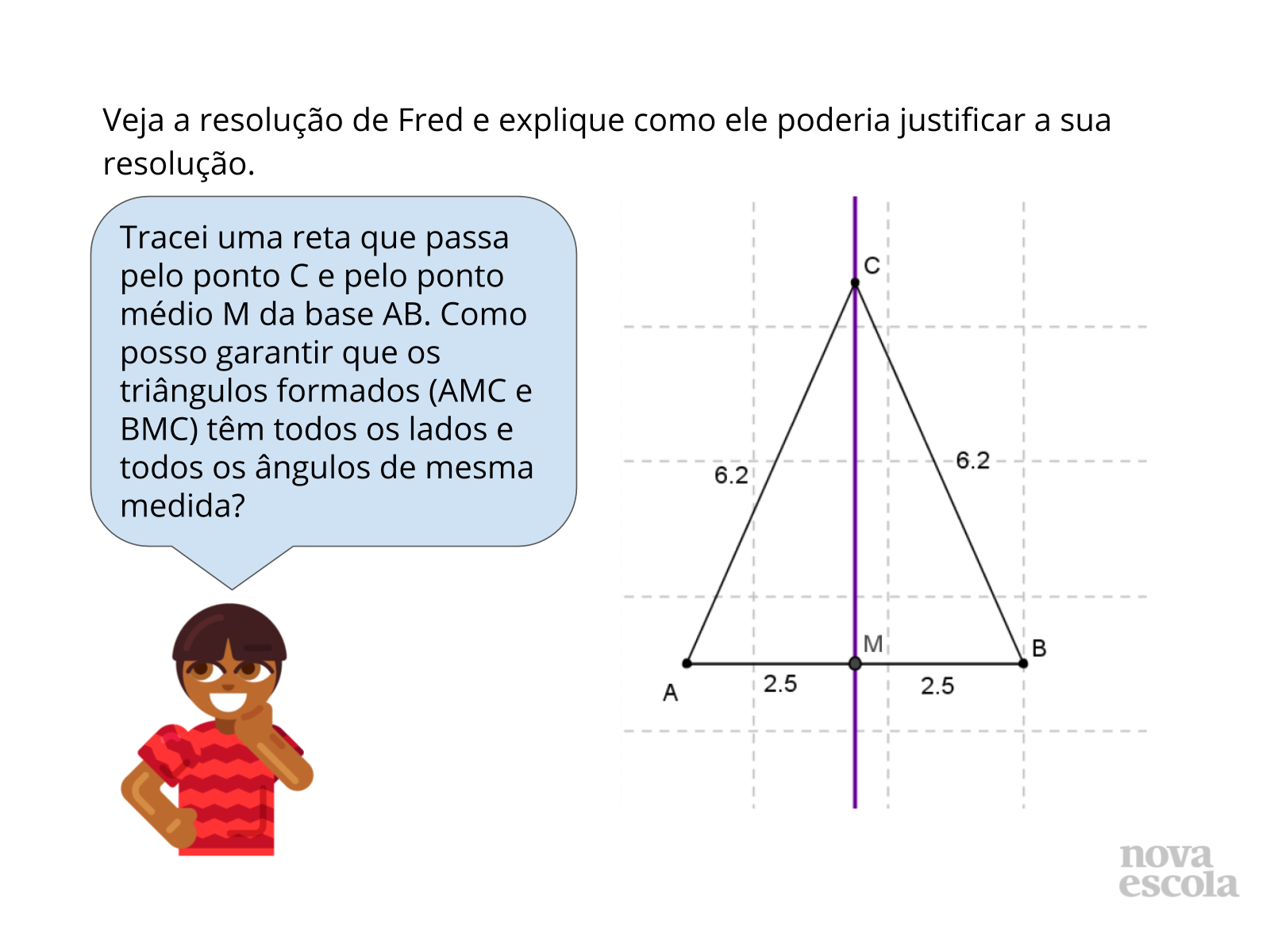
Orientação: Projete esta atividade (slides 7 e 8) ou entregue cópia da atividade impressa e leia o enunciado da questão para a classe (você também pode escolher alguns alunos para lerem em voz alta). Organize os alunos em duplas de trabalho heterogêneas. Solicite que os alunos pensem individualmente no problema e anotem as suas respostas em seus cadernos para, em seguida, discutirem com suas duplas. Depois, abra para que os alunos compartilhem as suas respostas coletivamente. Nesse momento, é importante que os alunos utilizem os critérios de congruência de triângulos para justificar a resolução apresentada por Fred. Por fim, utilize o slide 9 para formalizar a resolução com o uso de um critério de congruência de triângulos.
Propósito: incentivar que os alunos reconheçam que os critérios de congruência de triângulos podem ser usados para justificar a existência de eixo de simetria em figuras.
Discuta com a turma:
- É possível resolver mesmo sem conhecer a medida do lado MC?
- Como podemos classificar o triângulo ABC?
- O triângulo ABC possui outros eixos de simetria?
Materiais complementares para impressão:
Atividade principal
Tempo sugerido: 8 minutos (slides 7 a 9).
Orientação: Projete esta atividade (slides 7 e 8) ou entregue cópia da atividade impressa e leia o enunciado da questão para a classe (você também pode escolher alguns alunos para lerem em voz alta). Organize os alunos em duplas de trabalho heterogêneas. Solicite que os alunos pensem individualmente no problema e anotem as suas respostas em seus cadernos para, em seguida, discutirem com suas duplas. Depois, abra para que os alunos compartilhem as suas respostas coletivamente. Nesse momento, é importante que os alunos utilizem os critérios de congruência de triângulos para justificar a resolução apresentada por Fred. Por fim, utilize o slide 9 para formalizar a resolução com o uso de um critério de congruência de triângulos.
Propósito: incentivar que os alunos reconheçam que os critérios de congruência de triângulos podem ser usados para justificar a existência de eixo de simetria em figuras.
Discuta com a turma:
- É possível resolver mesmo sem conhecer a medida do lado MC?
- Como podemos classificar o triângulo ABC?
- O triângulo ABC possui outros eixos de simetria?
Atividade principal
Tempo sugerido: 8 minutos (slides 7 a 9).
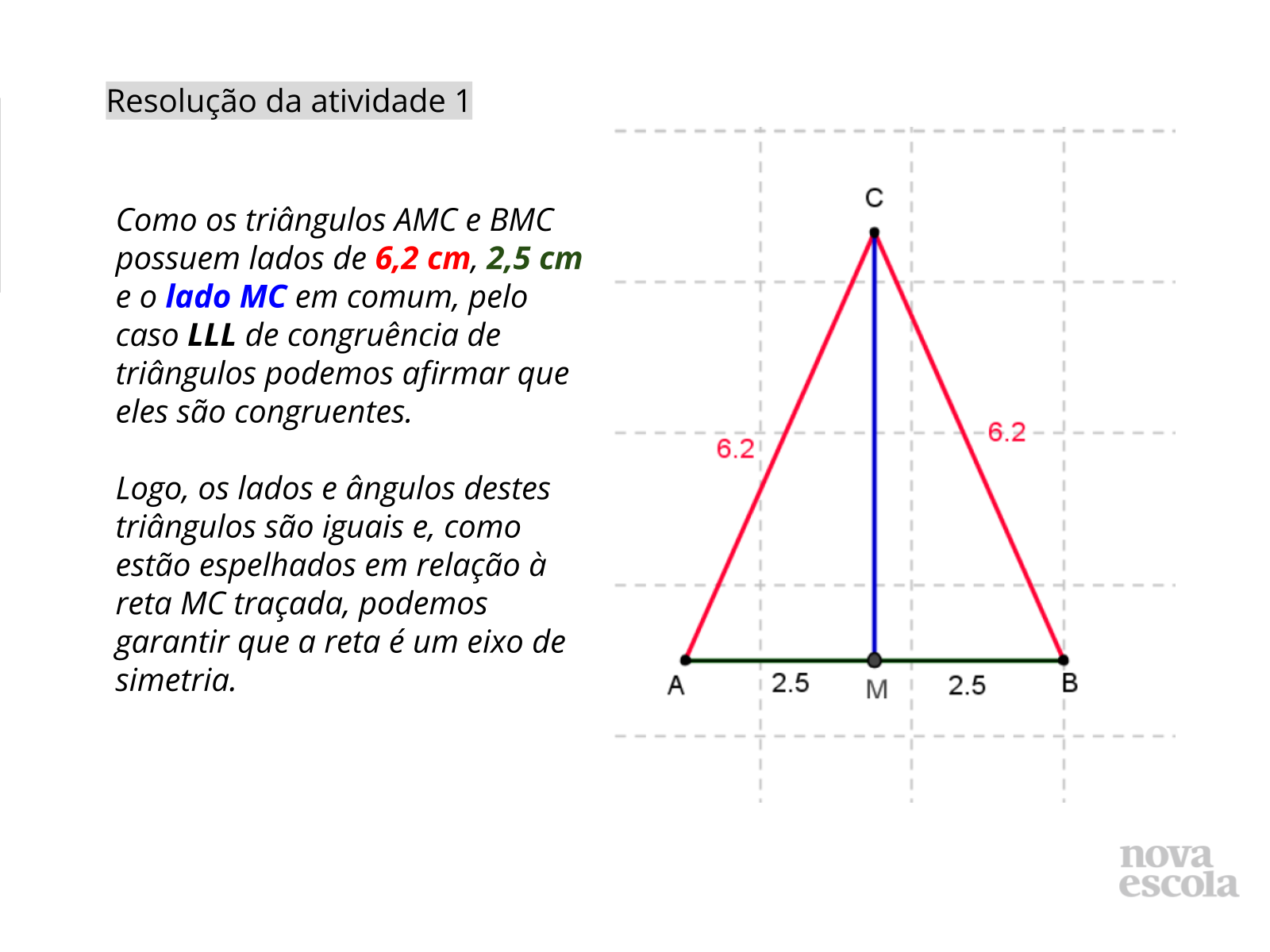
Orientação: Projete esta atividade (slides 7 e 8), ou entregue a cópia da atividade impressa e leia o enunciado da questão para a classe (você também pode escolher alguns alunos para lerem em voz alta). Organize os alunos em duplas de trabalho heterogêneas. Solicite que os alunos pensem individualmente no problema e anotem as suas respostas em seus cadernos para, em seguida, discutirem com suas duplas. Depois, abra para que os alunos compartilhem as suas respostas coletivamente. Nesse momento, é importante que os alunos utilizem os critérios de congruência de triângulos para justificar a resolução apresentada por Fred. Por fim, utilize o slide 9 para formalizar a resolução com o uso de um critério de congruência de triângulos.
Propósito: incentivar que os alunos reconheçam que os critérios de congruência de triângulos podem ser usados para justificar a existência de eixo de simetria em figuras.
Discuta com a turma:
- É possível resolver mesmo sem conhecer a medida do lado MC?
- Como podemos classificar o triângulo ABC?
- O triângulo ABC possui outros eixos de simetria?
Atividade principal
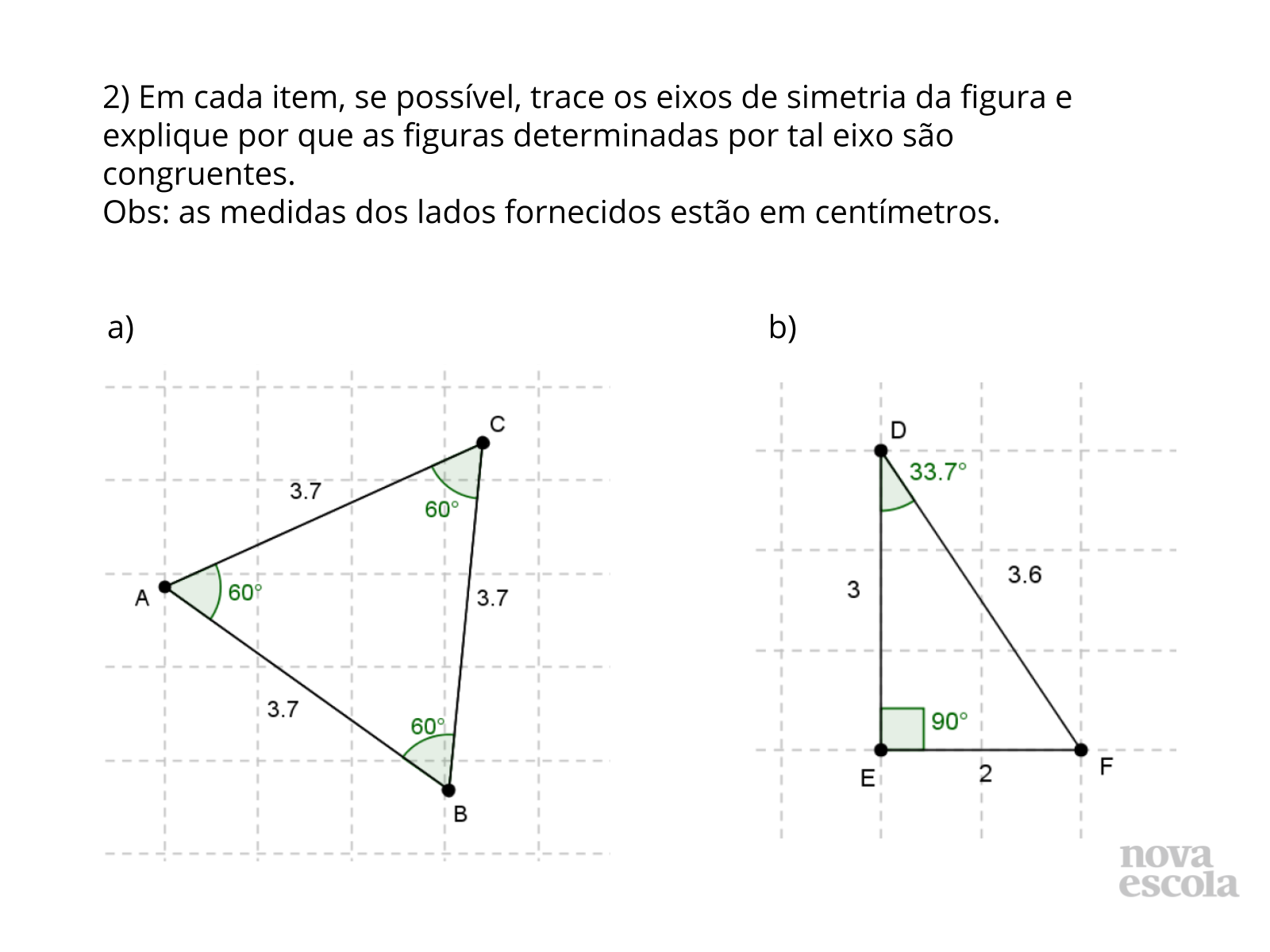
Tempo sugerido: 8 minutos (slides 10 e 11).
Orientação: Projete esta atividade (slides 10 e 11) ou entregue ou dê continuidade à atividade impressa e leia o enunciado da questão para a classe. Peça para os alunos resolverem a atividade nas duplas, traçando os eixos e registrando as justificativas. Oriente que utilizem os critérios de congruência de triângulos em suas explicações. .
Circule pela sala para observar como os alunos estão resolvendo o problema, sem informar os grupos se a resposta obtida por eles está correta ou não.
Se algum grupo terminar, peça que façam uma tabela relacionando a classificação da figura à quantidade de eixos de simetria que possui. Devem ser inseridas as seguintes classificações: triângulo isósceles, triângulo equilátero, triângulo escaleno, losango e quadrado.
Propósito: propiciar que os alunos analisem figuras, identifiquem eixos de simetria e utilizem critérios de congruência de triângulos para justificar a congruência.
Atividade principal
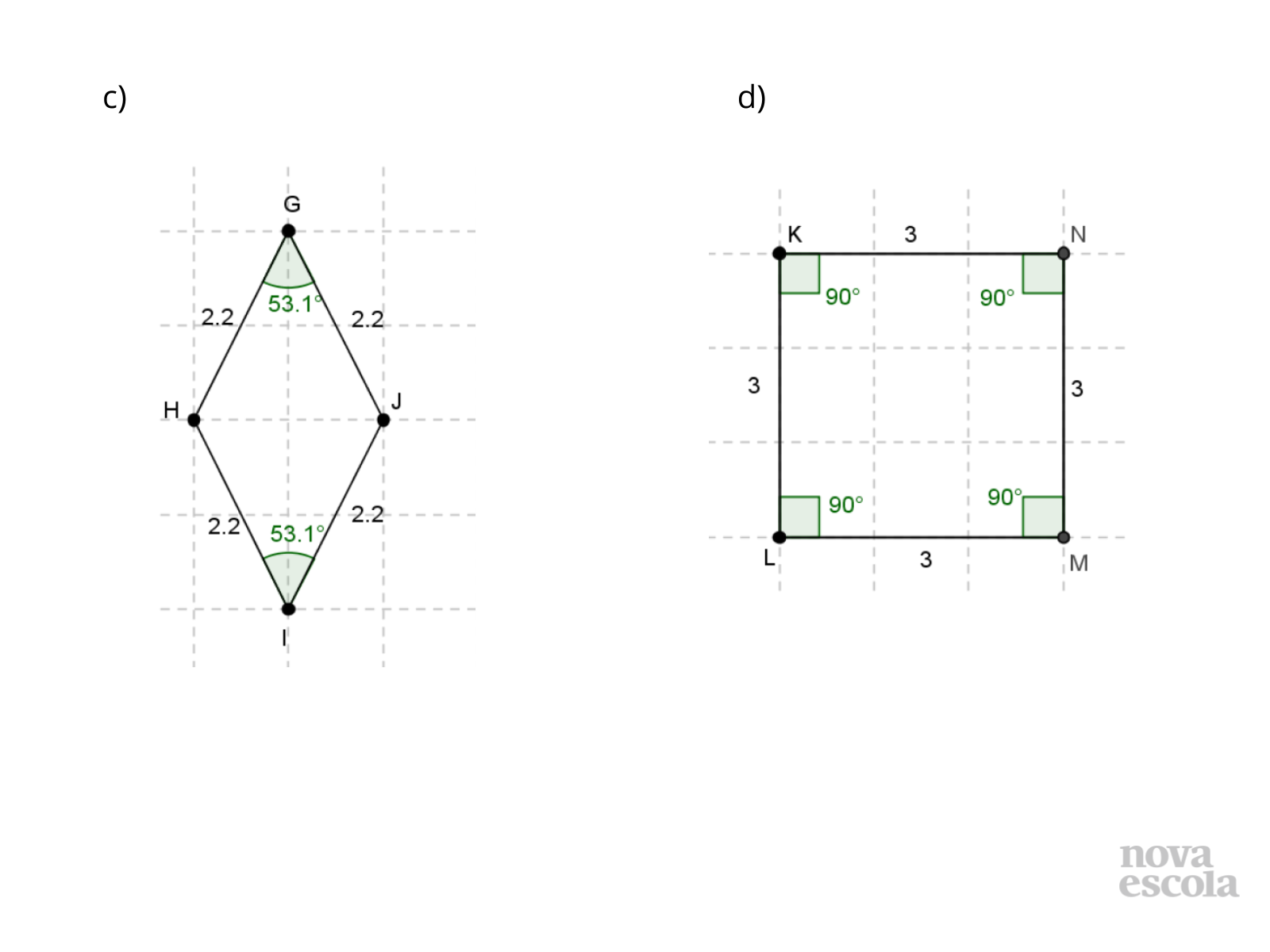
Tempo sugerido: 8 minutos (slides 10 e 11).
Orientação: Projete esta atividade (slides 10 e 11) ou entregue ou dê continuidade à atividade impressa e leia o enunciado da questão para a classe. Peça para os alunos resolverem a atividade nas duplas, traçando os eixos e registrando as justificativas. Oriente que utilizem os critérios de congruência de triângulos em suas explicações. .
Circule pela sala para observar como os alunos estão resolvendo o problema, sem informar os grupos se a resposta obtida por eles está correta ou não.
Se algum grupo terminar, peça que façam uma tabela relacionando a classificação da figura à quantidade de eixos de simetria que possui. Devem ser inseridas as seguintes classificações: triângulo isósceles, triângulo equilátero, triângulo escaleno, losango e quadrado.
Propósito: propiciar que os alunos analisem figuras, identifiquem eixos de simetria e utilizem critérios de congruência de triângulos para justificar a congruência.
Painel de soluções
Tempo sugerido: 12 minutos (slides 12 a 21).
Orientações: Explique que os itens serão discutidos na ordem.
Em cada item, inicie solicitando que os alunos digam se a figura possui ou não eixos de simetria e que exibam para a sala a localização de tais eixos e as suas justificativas. É importante que as diferentes respostas (tanto em relação à existência dos eixos de simetria quanto em relação aos tipos de justificativas apresentados), se houver, apareçam nesse momento de compartilhamento e, por isso, a observação feita das resoluções dos alunos no momento anterior é muito importante para decidir quais grupos chamar para falar em cada item.
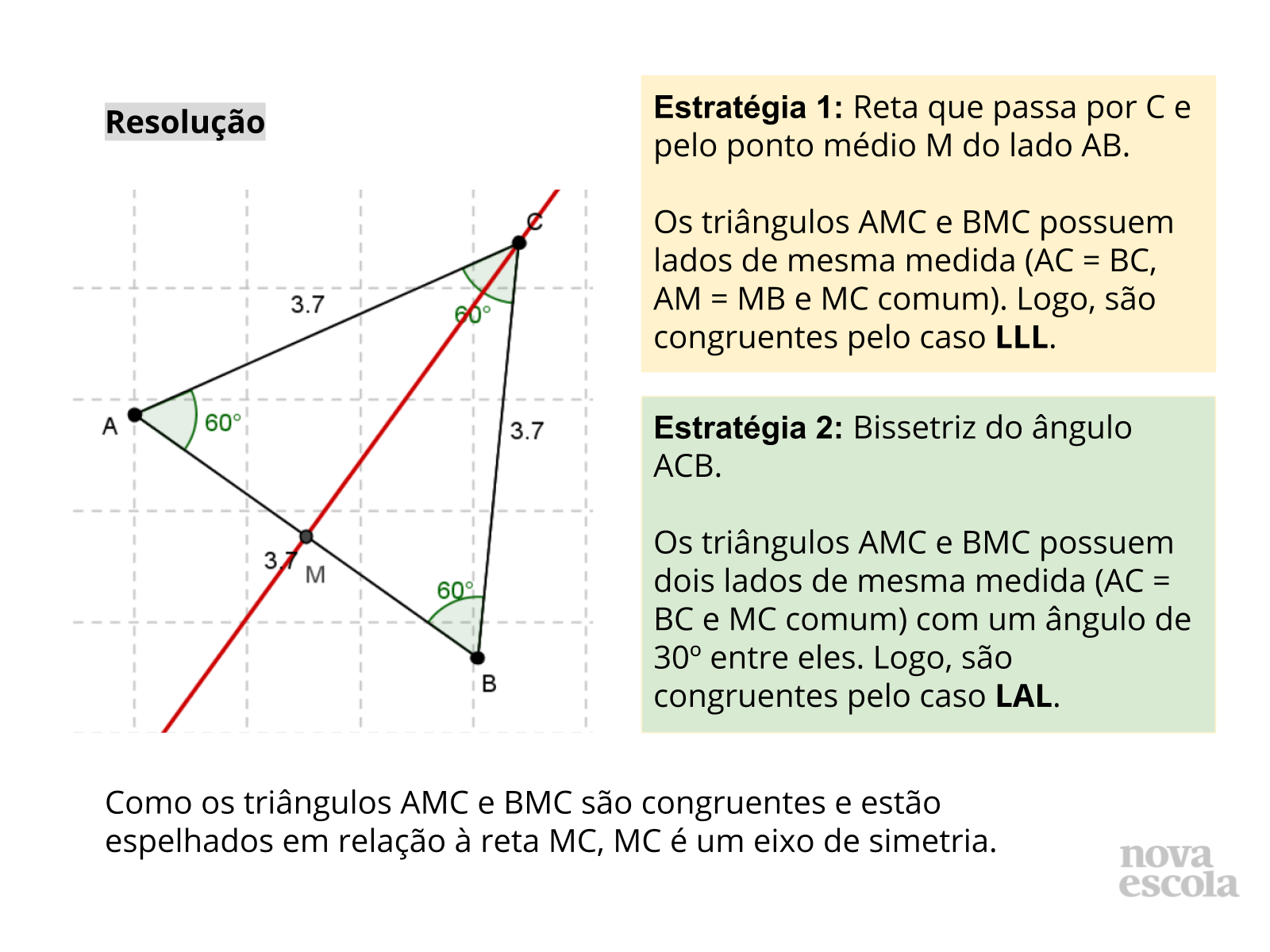
Nessa etapa da aula, é essencial que os critérios de congruência de triângulos sejam mencionados nas justificativas dos alunos. Para cada item, há um slide com a reprodução dos triângulos da atividade para apoiar a discussão e, em seguida, slides com a solução que contém os eixos de simetria e os critérios de congruência que podem ser utilizados para justificar (os slides com as soluções devem ser exibidos após a discussão feita pelos alunos).
Juntamente com a discussão sobre os eixos de simetria das figuras apresentadas, anote na lousa as relações que forem feitas entre as classificações das figuras (tipo de triângulo, tipo de quadrilátero) e a quantidade de eixos de simetria. Essas informações serão importantes para o encerramento da aula.
Propósito: propiciar que os alunos verifiquem a existência de eixos de simetria e elaborem justificativas utilizando os critérios de congruência de triângulos.
Discuta com a turma:
- Que estratégias podemos usar para decidir se uma figura possui eixos de simetria?
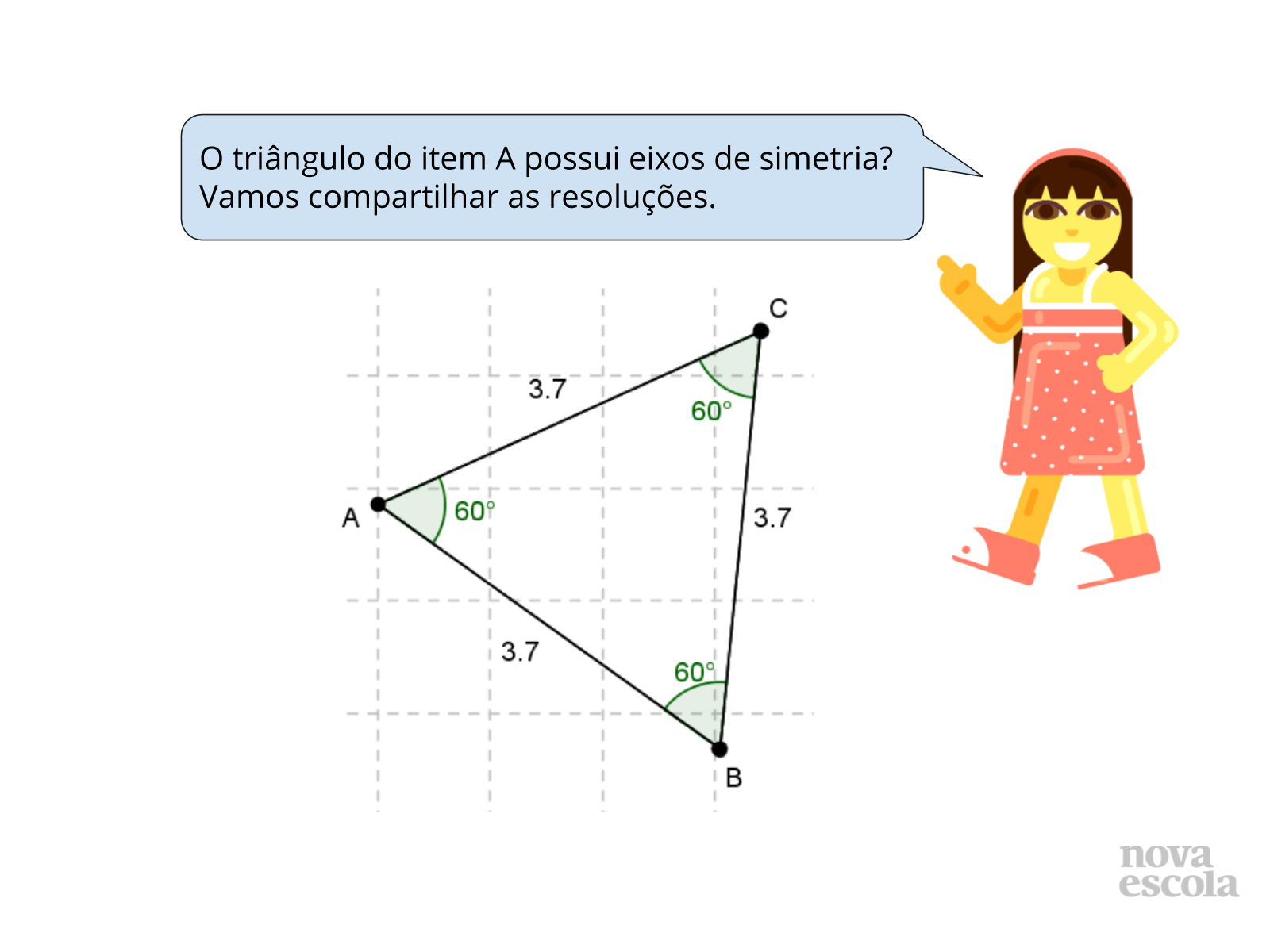
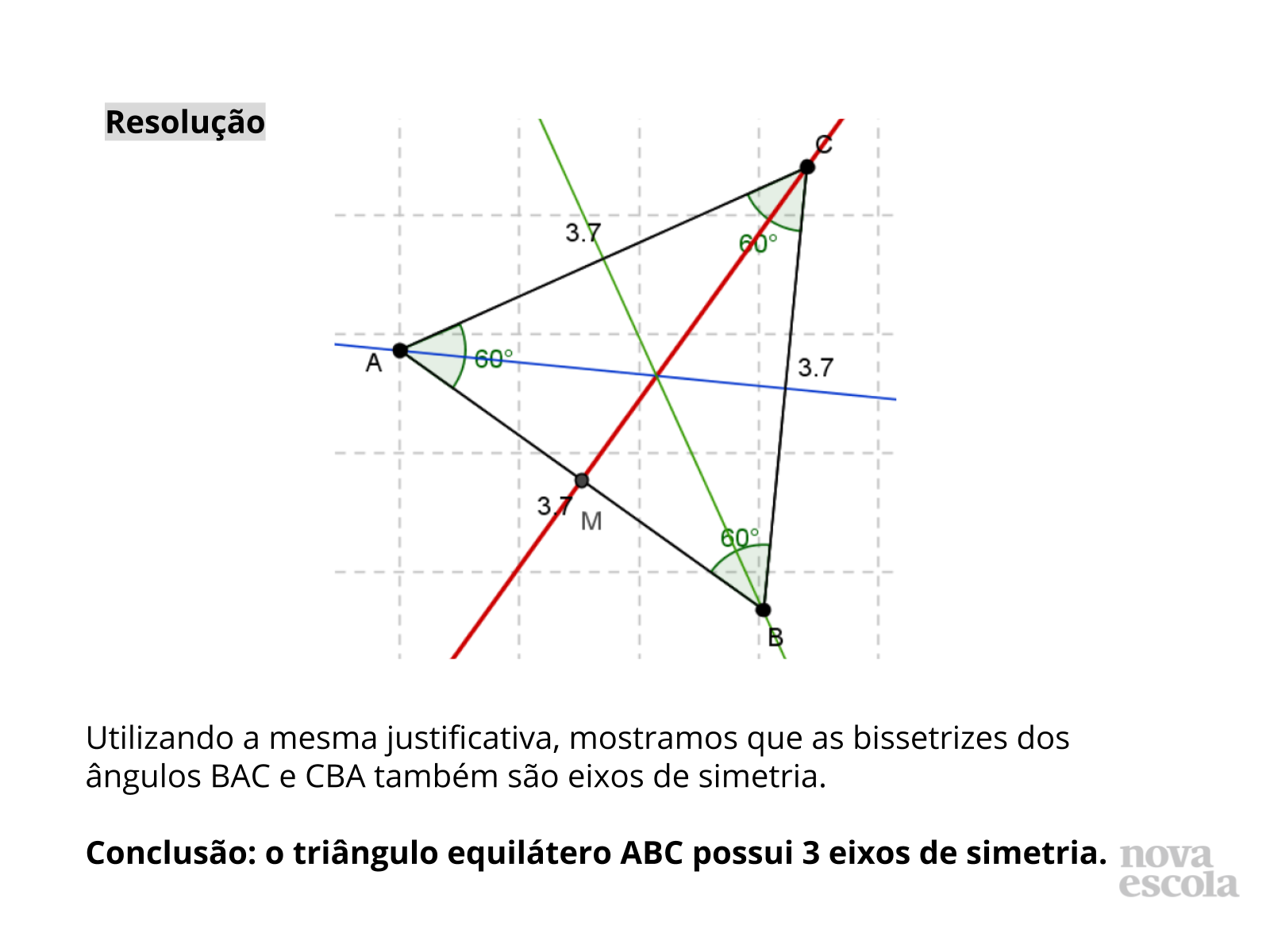
- No item a, qual é a classificação do triângulo apresentado? Um triângulo equilátero sempre possui 3 eixos de simetria? Por quê?
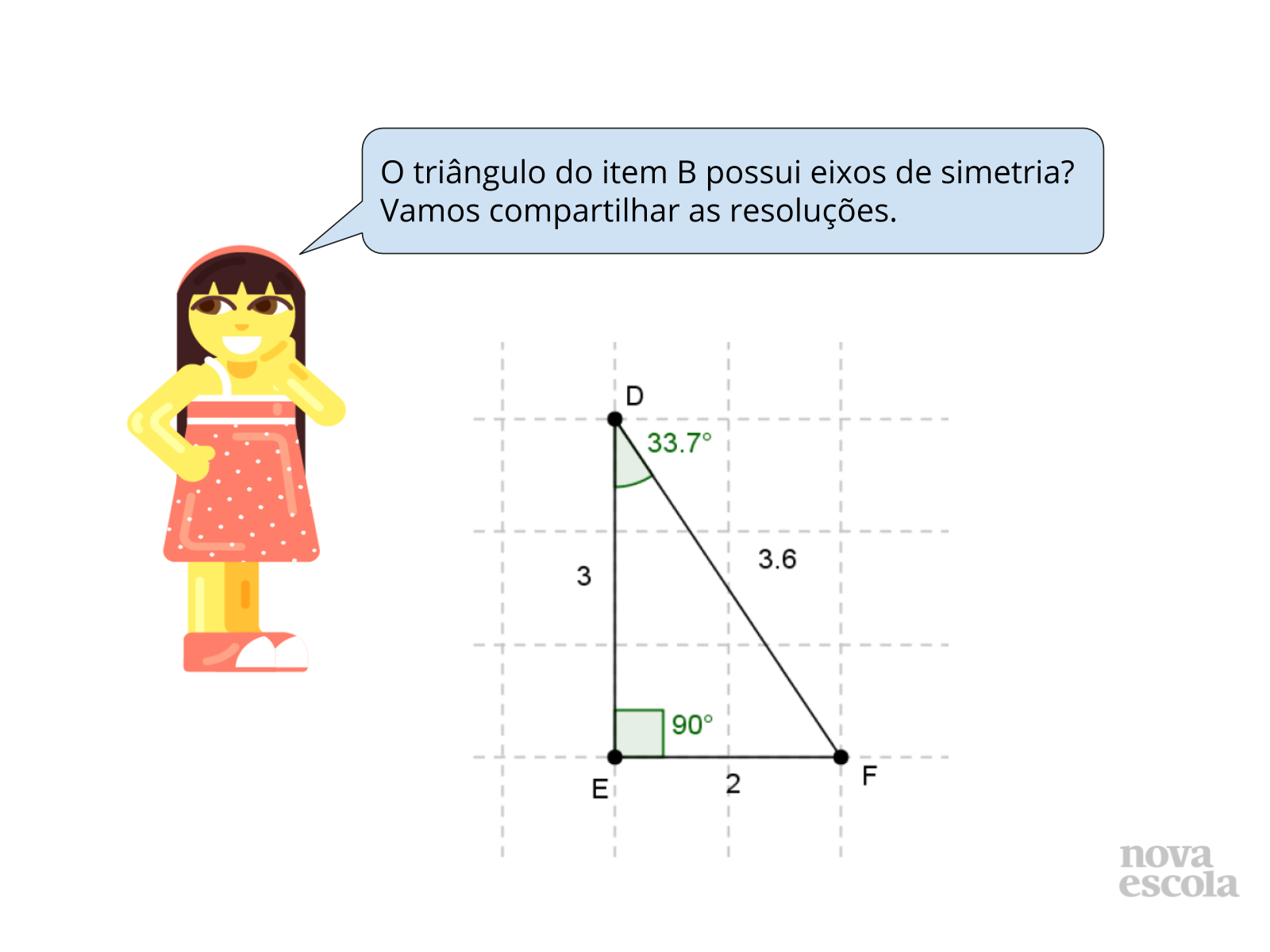
- No item b, qual é a classificação do triângulo apresentado? Um triângulo escaleno nunca possui eixos de simetria? Por quê?
- Será que um losango sempre possui 2 eixos de simetria? E o quadrado, sempre possui 4 eixos de simetria?
Painel de soluções
Tempo sugerido: 12 minutos (slides 12 a 21).
Orientações: Explique que os itens serão discutidos na ordem.
Em cada item, inicie solicitando que os alunos digam se a figura possui ou não eixos de simetria e que exibam para a sala a localização de tais eixos e as suas justificativas. É importante que as diferentes respostas (tanto em relação à existência dos eixos de simetria quanto em relação aos tipos de justificativas apresentados), se houver, apareçam nesse momento de compartilhamento e, por isso, a observação feita das resoluções dos alunos no momento anterior é muito importante para decidir quais grupos chamar para falar em cada item.
Nessa etapa da aula, é essencial que os critérios de congruência de triângulos sejam mencionados nas justificativas dos alunos. Para cada item, há um slide com a reprodução dos triângulos da atividade para apoiar a discussão e, em seguida, slides com a solução que contém os eixos de simetria e os critérios de congruência que podem ser utilizados para justificar (os slides com as soluções devem ser exibidos após a discussão feita pelos alunos).
Juntamente com a discussão sobre os eixos de simetria das figuras apresentadas, anote na lousa as relações que forem feitas entre as classificações das figuras (tipo de triângulo, tipo de quadrilátero) e a quantidade de eixos de simetria. Essas informações serão importantes para o encerramento da aula.
Propósito: propiciar que os alunos verifiquem a existência de eixos de simetria e elaborem justificativas utilizando os critérios de congruência de triângulos.
Discuta com a turma:
- Que estratégias podemos usar para decidir se uma figura possui eixos de simetria?
- No item a, qual é a classificação do triângulo apresentado? Um triângulo equilátero sempre possui 3 eixos de simetria? Por quê?
- No item b, qual é a classificação do triângulo apresentado? Um triângulo escaleno nunca possui eixos de simetria? Por quê?
- Será que um losango sempre possui 2 eixos de simetria? E o quadrado, sempre possui 4 eixos de simetria?
Painel de soluções
Tempo sugerido: 12 minutos (slides 12 a 21).
Orientações: Explique que os itens serão discutidos na ordem.
Em cada item, inicie solicitando que os alunos digam se a figura possui ou não eixos de simetria e que exibam para a sala a localização de tais eixos e as suas justificativas. É importante que as diferentes respostas (tanto em relação à existência dos eixos de simetria quanto em relação aos tipos de justificativas apresentados), se houver, apareçam nesse momento de compartilhamento e, por isso, a observação feita das resoluções dos alunos no momento anterior é muito importante para decidir quais grupos chamar para falar em cada item.
Nessa etapa da aula, é essencial que os critérios de congruência de triângulos sejam mencionados nas justificativas dos alunos. Para cada item, há um slide com a reprodução dos triângulos da atividade para apoiar a discussão e, em seguida, slides com a solução que contém os eixos de simetria e os critérios de congruência que podem ser utilizados para justificar (os slides com as soluções devem ser exibidos após a discussão feita pelos alunos).
Juntamente com a discussão sobre os eixos de simetria das figuras apresentadas, anote na lousa as relações que forem feitas entre as classificações das figuras (tipo de triângulo, tipo de quadrilátero) e a quantidade de eixos de simetria. Essas informações serão importantes para o encerramento da aula.
Propósito: propiciar que os alunos verifiquem a existência de eixos de simetria e elaborem justificativas utilizando os critérios de congruência de triângulos.
Discuta com a turma:
- Que estratégias podemos usar para decidir se uma figura possui eixos de simetria?
- No item a, qual é a classificação do triângulo apresentado? Um triângulo equilátero sempre possui 3 eixos de simetria? Por quê?
- No item b, qual é a classificação do triângulo apresentado? Um triângulo escaleno nunca possui eixos de simetria? Por quê?
- Será que um losango sempre possui 2 eixos de simetria? E o quadrado, sempre possui 4 eixos de simetria?
Painel de soluções
Tempo sugerido: 12 minutos (slides 12 a 21).
Orientações: Explique que os itens serão discutidos na ordem.
Em cada item, inicie solicitando que os alunos digam se a figura possui ou não eixos de simetria e que exibam para a sala a localização de tais eixos e as suas justificativas. É importante que as diferentes respostas (tanto em relação à existência dos eixos de simetria quanto em relação aos tipos de justificativas apresentados), se houver, apareçam nesse momento de compartilhamento e, por isso, a observação feita das resoluções dos alunos no momento anterior é muito importante para decidir quais grupos chamar para falar em cada item.
Nessa etapa da aula, é essencial que os critérios de congruência de triângulos sejam mencionados nas justificativas dos alunos. Para cada item, há um slide com a reprodução dos triângulos da atividade para apoiar a discussão e, em seguida, slides com a solução que contém os eixos de simetria e os critérios de congruência que podem ser utilizados para justificar (os slides com as soluções devem ser exibidos após a discussão feita pelos alunos).
Juntamente com a discussão sobre os eixos de simetria das figuras apresentadas, anote na lousa as relações que forem feitas entre as classificações das figuras (tipo de triângulo, tipo de quadrilátero) e a quantidade de eixos de simetria. Essas informações serão importantes para o encerramento da aula.
Propósito: propiciar que os alunos verifiquem a existência de eixos de simetria e elaborem justificativas utilizando os critérios de congruência de triângulos.
Discuta com a turma:
- Que estratégias podemos usar para decidir se uma figura possui eixos de simetria?
- No item a, qual é a classificação do triângulo apresentado? Um triângulo equilátero sempre possui 3 eixos de simetria? Por quê?
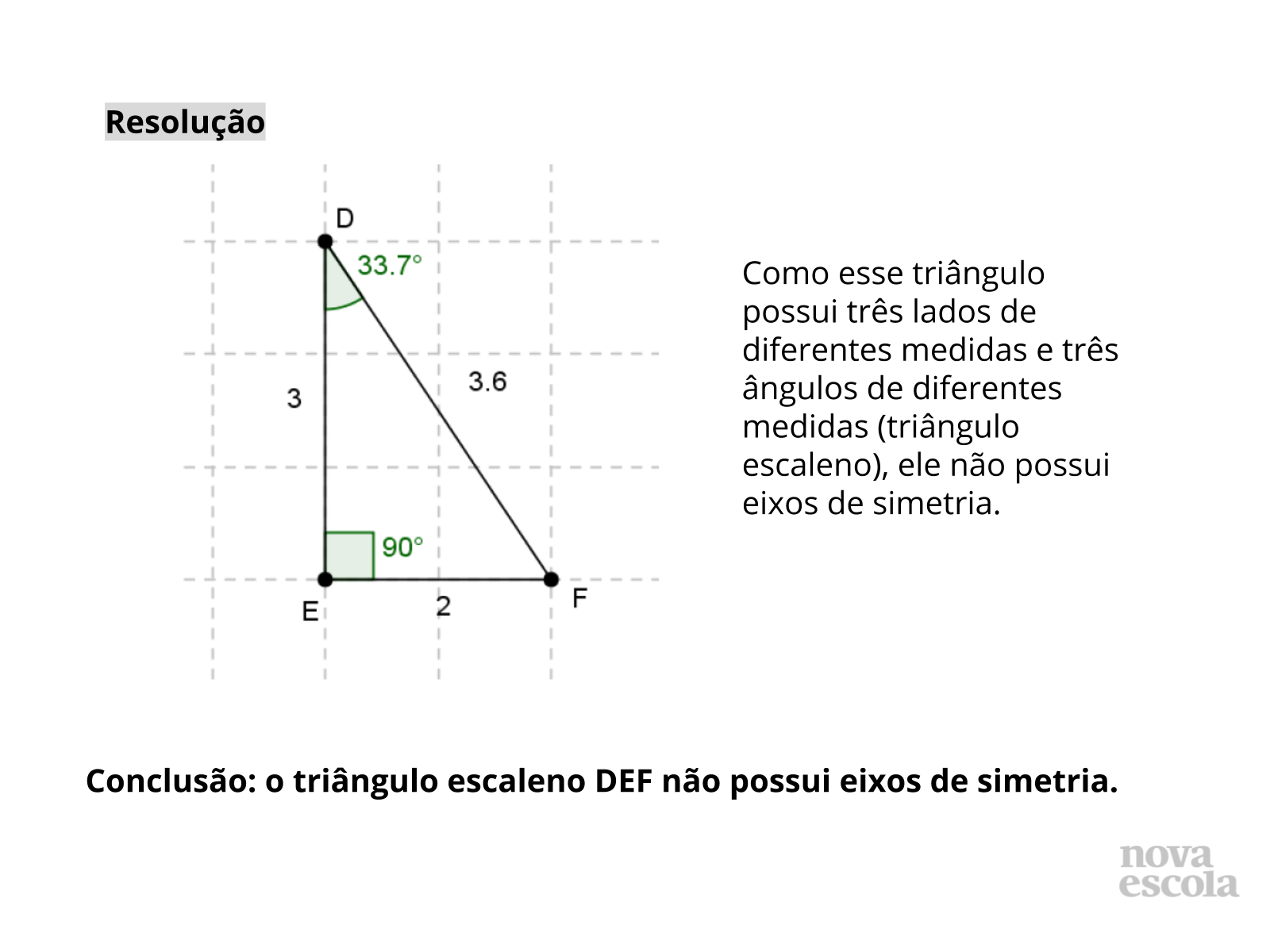
- No item b, qual é a classificação do triângulo apresentado? Um triângulo escaleno nunca possui eixos de simetria? Por quê?
- Será que um losango sempre possui 2 eixos de simetria? E o quadrado, sempre possui 4 eixos de simetria?
Painel de soluções
Tempo sugerido: 12 minutos (slides 12 a 21).
Orientações: Explique que os itens serão discutidos na ordem.
Em cada item, inicie solicitando que os alunos digam se a figura possui ou não eixos de simetria e que exibam para a sala a localização de tais eixos e as suas justificativas. É importante que as diferentes respostas (tanto em relação à existência dos eixos de simetria quanto em relação aos tipos de justificativas apresentados), se houver, apareçam nesse momento de compartilhamento e, por isso, a observação feita das resoluções dos alunos no momento anterior é muito importante para decidir quais grupos chamar para falar em cada item.
Nessa etapa da aula, é essencial que os critérios de congruência de triângulos sejam mencionados nas justificativas dos alunos. Para cada item, há um slide com a reprodução dos triângulos da atividade para apoiar a discussão e, em seguida, slides com a solução que contém os eixos de simetria e os critérios de congruência que podem ser utilizados para justificar (os slides com as soluções devem ser exibidos após a discussão feita pelos alunos).
Juntamente com a discussão sobre os eixos de simetria das figuras apresentadas, anote na lousa as relações que forem feitas entre as classificações das figuras (tipo de triângulo, tipo de quadrilátero) e a quantidade de eixos de simetria. Essas informações serão importantes para o encerramento da aula.
Propósito: propiciar que os alunos verifiquem a existência de eixos de simetria e elaborem justificativas utilizando os critérios de congruência de triângulos.
Discuta com a turma:
- Que estratégias podemos usar para decidir se uma figura possui eixos de simetria?
- No item a, qual é a classificação do triângulo apresentado? Um triângulo equilátero sempre possui 3 eixos de simetria? Por quê?
- No item b, qual é a classificação do triângulo apresentado? Um triângulo escaleno nunca possui eixos de simetria? Por quê?
- Será que um losango sempre possui 2 eixos de simetria? E o quadrado, sempre possui 4 eixos de simetria?
Painel de soluções
Tempo sugerido: 12 minutos (slides 12 a 21).
Orientações: Explique que os itens serão discutidos na ordem.
Em cada item, inicie solicitando que os alunos digam se a figura possui ou não eixos de simetria e que exibam para a sala a localização de tais eixos e as suas justificativas. É importante que as diferentes respostas (tanto em relação à existência dos eixos de simetria quanto em relação aos tipos de justificativas apresentados), se houver, apareçam nesse momento de compartilhamento e, por isso, a observação feita das resoluções dos alunos no momento anterior é muito importante para decidir quais grupos chamar para falar em cada item.
Nessa etapa da aula, é essencial que os critérios de congruência de triângulos sejam mencionados nas justificativas dos alunos. Para cada item, há um slide com a reprodução dos triângulos da atividade para apoiar a discussão e, em seguida, slides com a solução que contém os eixos de simetria e os critérios de congruência que podem ser utilizados para justificar (os slides com as soluções devem ser exibidos após a discussão feita pelos alunos).
Juntamente com a discussão sobre os eixos de simetria das figuras apresentadas, anote na lousa as relações que forem feitas entre as classificações das figuras (tipo de triângulo, tipo de quadrilátero) e a quantidade de eixos de simetria. Essas informações serão importantes para o encerramento da aula.
Propósito: propiciar que os alunos verifiquem a existência de eixos de simetria e elaborem justificativas utilizando os critérios de congruência de triângulos.
Discuta com a turma:
- Que estratégias podemos usar para decidir se uma figura possui eixos de simetria?
- No item a, qual é a classificação do triângulo apresentado? Um triângulo equilátero sempre possui 3 eixos de simetria? Por quê?
- No item b, qual é a classificação do triângulo apresentado? Um triângulo escaleno nunca possui eixos de simetria? Por quê?
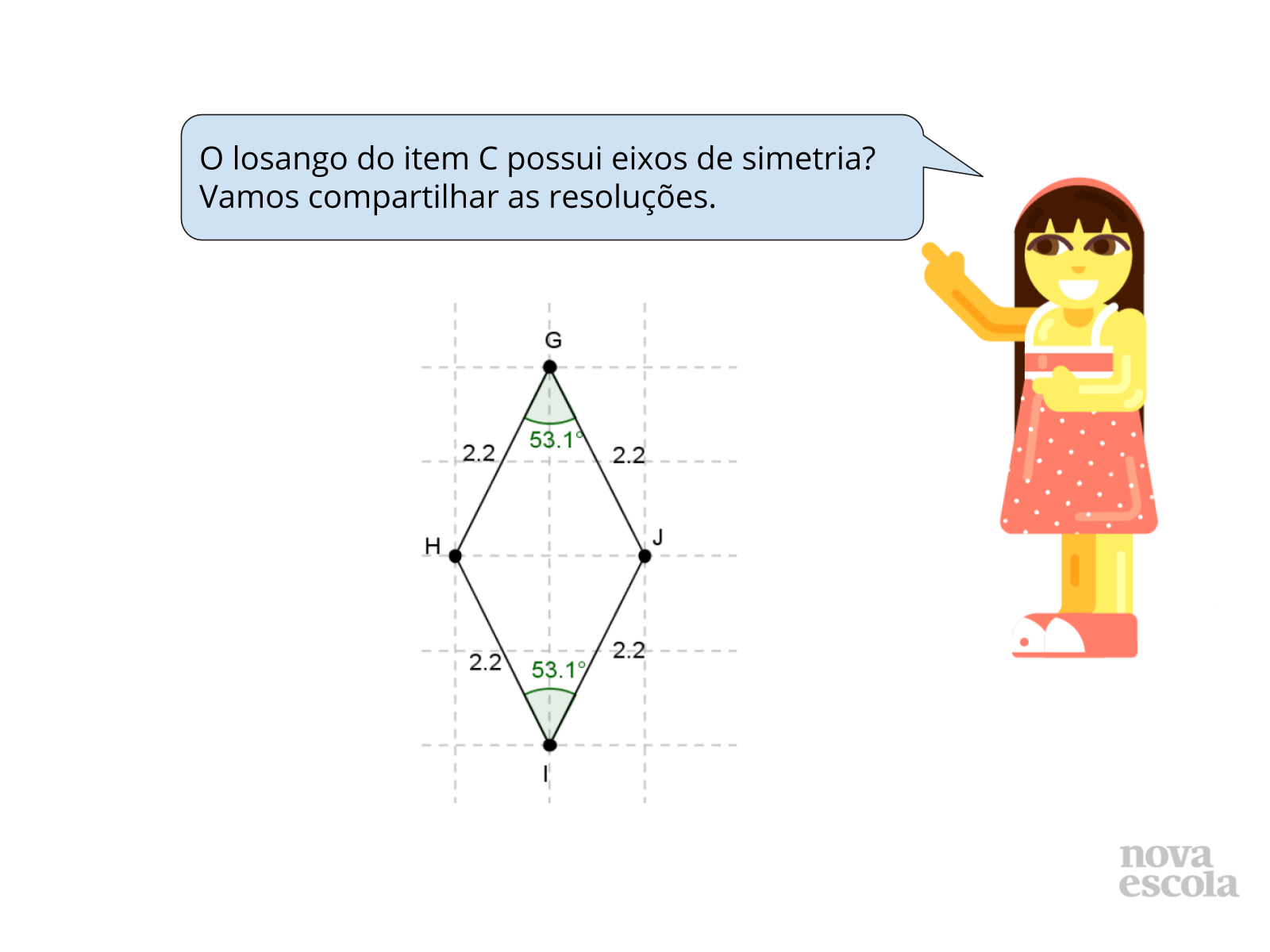
- Será que um losango sempre possui 2 eixos de simetria? E o quadrado, sempre possui 4 eixos de simetria?
Painel de soluções
Tempo sugerido: 12 minutos (slides 12 a 21).
Orientações: Explique que os itens serão discutidos na ordem.
Em cada item, inicie solicitando que os alunos digam se a figura possui ou não eixos de simetria e que exibam para a sala a localização de tais eixos e as suas justificativas. É importante que as diferentes respostas (tanto em relação à existência dos eixos de simetria quanto em relação aos tipos de justificativas apresentados), se houver, apareçam nesse momento de compartilhamento e, por isso, a observação feita das resoluções dos alunos no momento anterior é muito importante para decidir quais grupos chamar para falar em cada item.
Nessa etapa da aula, é essencial que os critérios de congruência de triângulos sejam mencionados nas justificativas dos alunos. Para cada item, há um slide com a reprodução dos triângulos da atividade para apoiar a discussão e, em seguida, slides com a solução que contém os eixos de simetria e os critérios de congruência que podem ser utilizados para justificar (os slides com as soluções devem ser exibidos após a discussão feita pelos alunos).
Juntamente com a discussão sobre os eixos de simetria das figuras apresentadas, anote na lousa as relações que forem feitas entre as classificações das figuras (tipo de triângulo, tipo de quadrilátero) e a quantidade de eixos de simetria. Essas informações serão importantes para o encerramento da aula.
Propósito: propiciar que os alunos verifiquem a existência de eixos de simetria e elaborem justificativas utilizando os critérios de congruência de triângulos.
Discuta com a turma:
- Que estratégias podemos usar para decidir se uma figura possui eixos de simetria?
- No item a, qual é a classificação do triângulo apresentado? Um triângulo equilátero sempre possui 3 eixos de simetria? Por quê?
- No item b, qual é a classificação do triângulo apresentado? Um triângulo escaleno nunca possui eixos de simetria? Por quê?
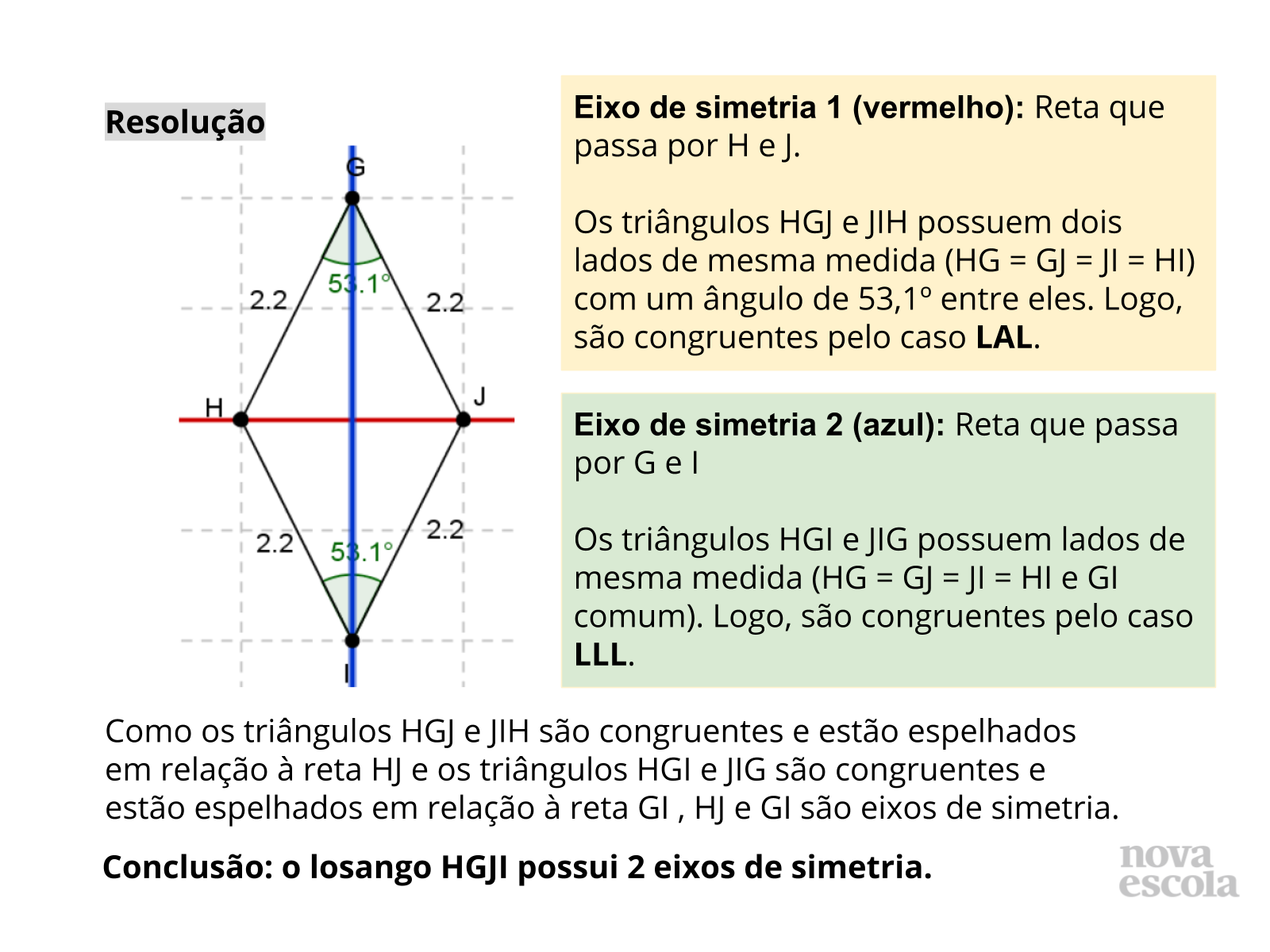
- Será que um losango sempre possui 2 eixos de simetria? E o quadrado, sempre possui 4 eixos de simetria?
Painel de soluções
Tempo sugerido: 12 minutos (slides 12 a 21).
Orientações: Explique que os itens serão discutidos na ordem.
Em cada item, inicie solicitando que os alunos digam se a figura possui ou não eixos de simetria e que exibam para a sala a localização de tais eixos e as suas justificativas. É importante que as diferentes respostas (tanto em relação à existência dos eixos de simetria quanto em relação aos tipos de justificativas apresentados), se houver, apareçam nesse momento de compartilhamento e, por isso, a observação feita das resoluções dos alunos no momento anterior é muito importante para decidir quais grupos chamar para falar em cada item.
Nessa etapa da aula, é essencial que os critérios de congruência de triângulos sejam mencionados nas justificativas dos alunos. Para cada item, há um slide com a reprodução dos triângulos da atividade para apoiar a discussão e, em seguida, slides com a solução que contém os eixos de simetria e os critérios de congruência que podem ser utilizados para justificar (os slides com as soluções devem ser exibidos após a discussão feita pelos alunos).
Juntamente com a discussão sobre os eixos de simetria das figuras apresentadas, anote na lousa as relações que forem feitas entre as classificações das figuras (tipo de triângulo, tipo de quadrilátero) e a quantidade de eixos de simetria. Essas informações serão importantes para o encerramento da aula.
Propósito: propiciar que os alunos verifiquem a existência de eixos de simetria e elaborem justificativas utilizando os critérios de congruência de triângulos.
Discuta com a turma:
- Que estratégias podemos usar para decidir se uma figura possui eixos de simetria?
- No item a, qual é a classificação do triângulo apresentado? Um triângulo equilátero sempre possui 3 eixos de simetria? Por quê?
- No item b, qual é a classificação do triângulo apresentado? Um triângulo escaleno nunca possui eixos de simetria? Por quê?
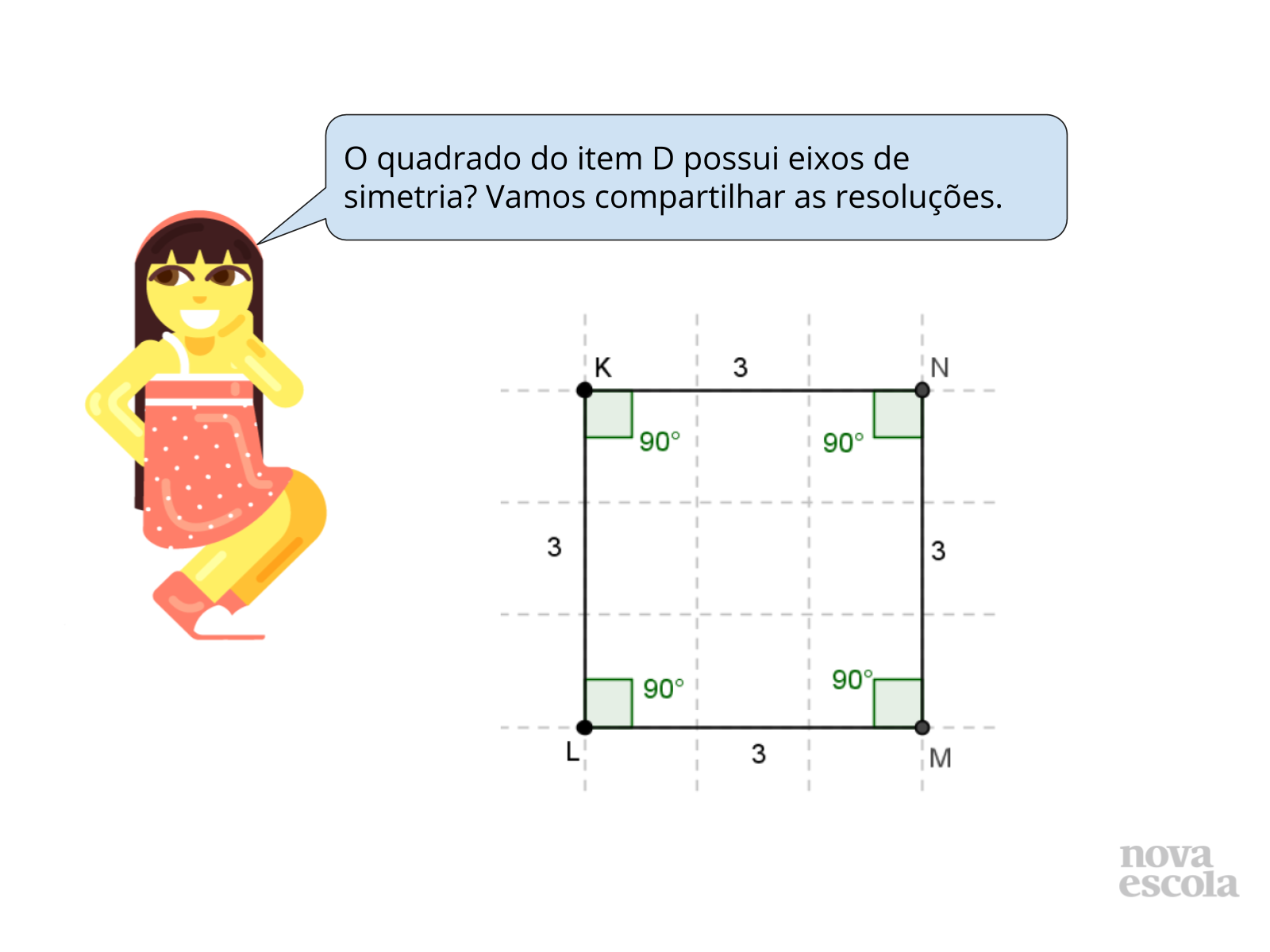
- Será que um losango sempre possui 2 eixos de simetria? E o quadrado, sempre possui 4 eixos de simetria?
Painel de soluções
Tempo sugerido: 12 minutos (slides 12 a 21).
Orientações: Explique que os itens serão discutidos na ordem.
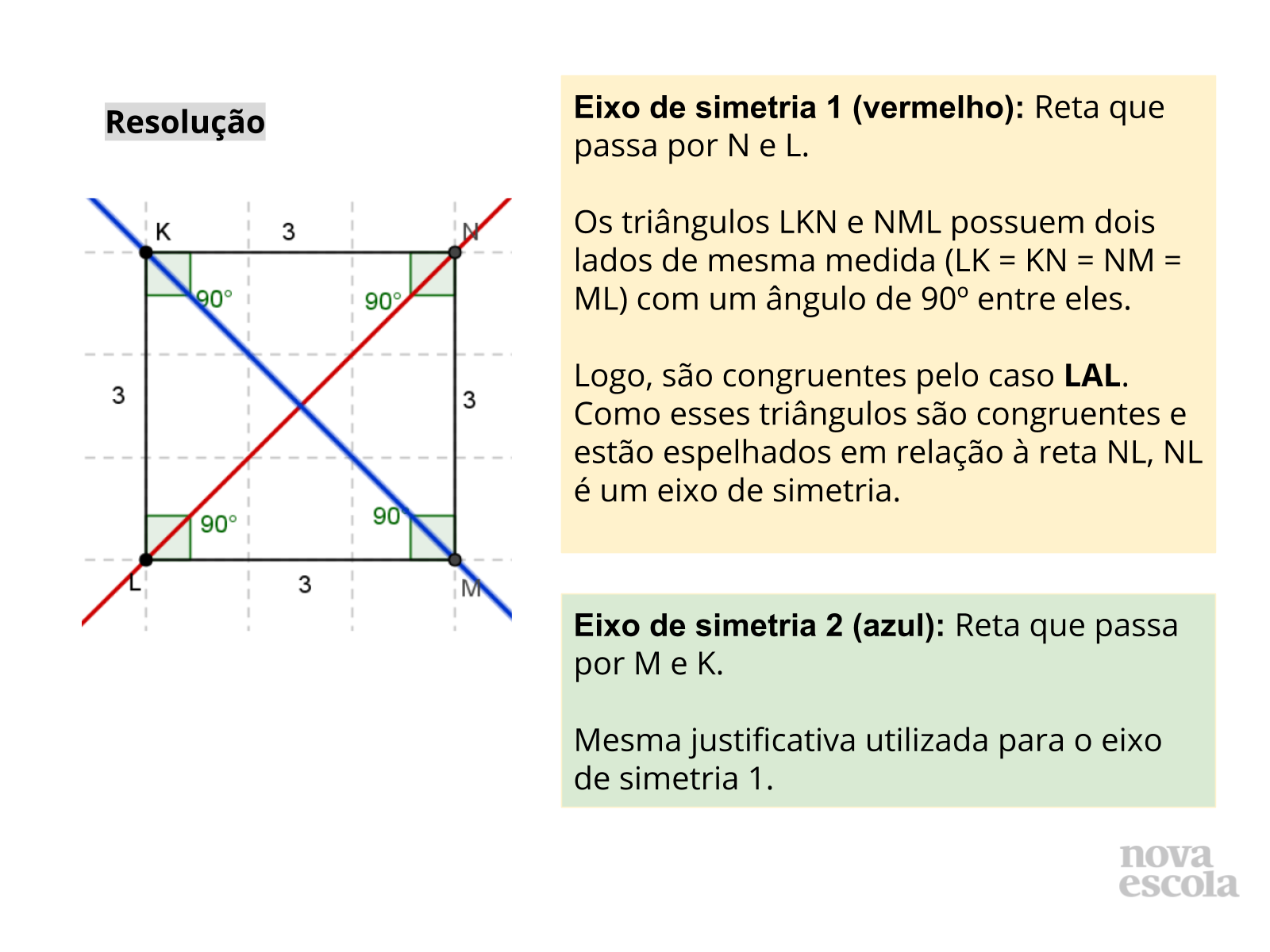
Em cada item, inicie solicitando que os alunos digam se a figura possui ou não eixos de simetria e que exibam para a sala a localização de tais eixos e as suas justificativas. É importante que as diferentes respostas (tanto em relação à existência dos eixos de simetria quanto em relação aos tipos de justificativas apresentados), se houver, apareçam nesse momento de compartilhamento e, por isso, a observação feita das resoluções dos alunos no momento anterior é muito importante para decidir quais grupos chamar para falar em cada item.
Nessa etapa da aula, é essencial que os critérios de congruência de triângulos sejam mencionados nas justificativas dos alunos. Para cada item, há um slide com a reprodução dos triângulos da atividade para apoiar a discussão e, em seguida, slides com a solução que contém os eixos de simetria e os critérios de congruência que podem ser utilizados para justificar (os slides com as soluções devem ser exibidos após a discussão feita pelos alunos).
Juntamente com a discussão sobre os eixos de simetria das figuras apresentadas, anote na lousa as relações que forem feitas entre as classificações das figuras (tipo de triângulo, tipo de quadrilátero) e a quantidade de eixos de simetria. Essas informações serão importantes para o encerramento da aula.
Propósito: propiciar que os alunos verifiquem a existência de eixos de simetria e elaborem justificativas utilizando os critérios de congruência de triângulos.
Discuta com a turma:
- Que estratégias podemos usar para decidir se uma figura possui eixos de simetria?
- No item a, qual é a classificação do triângulo apresentado? Um triângulo equilátero sempre possui 3 eixos de simetria? Por quê?
- No item b, qual é a classificação do triângulo apresentado? Um triângulo escaleno nunca possui eixos de simetria? Por quê?
- Será que um losango sempre possui 2 eixos de simetria? E o quadrado, sempre possui 4 eixos de simetria?
Painel de soluções
Tempo sugerido: 12 minutos (slides 12 a 21).
Orientações: Explique que os itens serão discutidos na ordem.
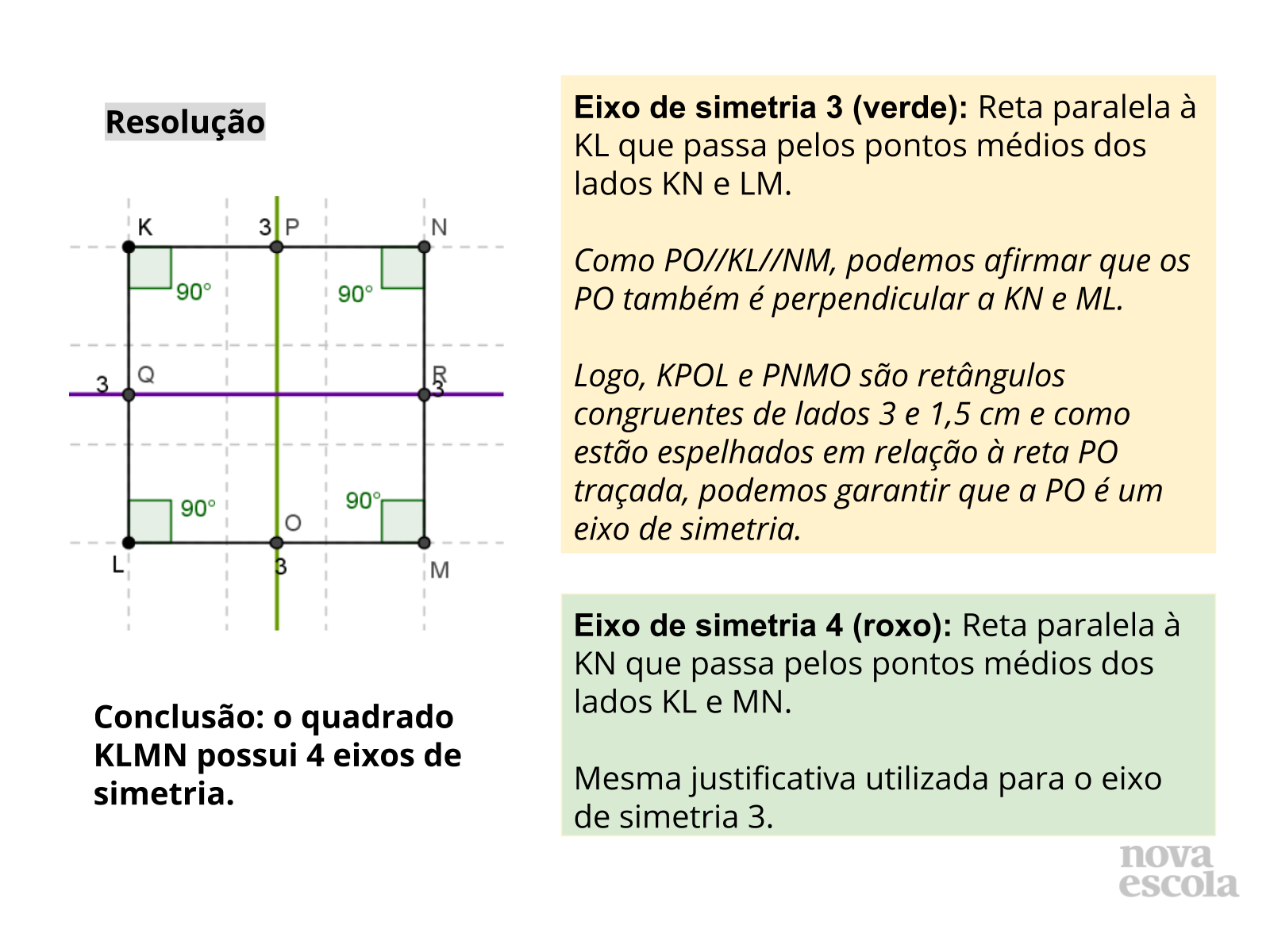
Em cada item, inicie solicitando que os alunos digam se a figura possui ou não eixos de simetria e que exibam para a sala a localização de tais eixos e as suas justificativas. É importante que as diferentes respostas (tanto em relação à existência dos eixos de simetria quanto em relação aos tipos de justificativas apresentados), se houver, apareçam nesse momento de compartilhamento e, por isso, a observação feita das resoluções dos alunos no momento anterior é muito importante para decidir quais grupos chamar para falar em cada item.
Nessa etapa da aula, é essencial que os critérios de congruência de triângulos sejam mencionados nas justificativas dos alunos. Para cada item, há um slide com a reprodução dos triângulos da atividade para apoiar a discussão e, em seguida, slides com a solução que contém os eixos de simetria e os critérios de congruência que podem ser utilizados para justificar (os slides com as soluções devem ser exibidos após a discussão feita pelos alunos).
Juntamente com a discussão sobre os eixos de simetria das figuras apresentadas, anote na lousa as relações que forem feitas entre as classificações das figuras (tipo de triângulo, tipo de quadrilátero) e a quantidade de eixos de simetria. Essas informações serão importantes para o encerramento da aula.
Propósito: propiciar que os alunos verifiquem a existência de eixos de simetria e elaborem justificativas utilizando os critérios de congruência de triângulos.
Discuta com a turma:
- Que estratégias podemos usar para decidir se uma figura possui eixos de simetria?
- No item a, qual é a classificação do triângulo apresentado? Um triângulo equilátero sempre possui 3 eixos de simetria? Por quê?
- No item b, qual é a classificação do triângulo apresentado? Um triângulo escaleno nunca possui eixos de simetria? Por quê?
- Será que um losango sempre possui 2 eixos de simetria? E o quadrado, sempre possui 4 eixos de simetria?
Encerramento
Tempo sugerido: 2 minutos.
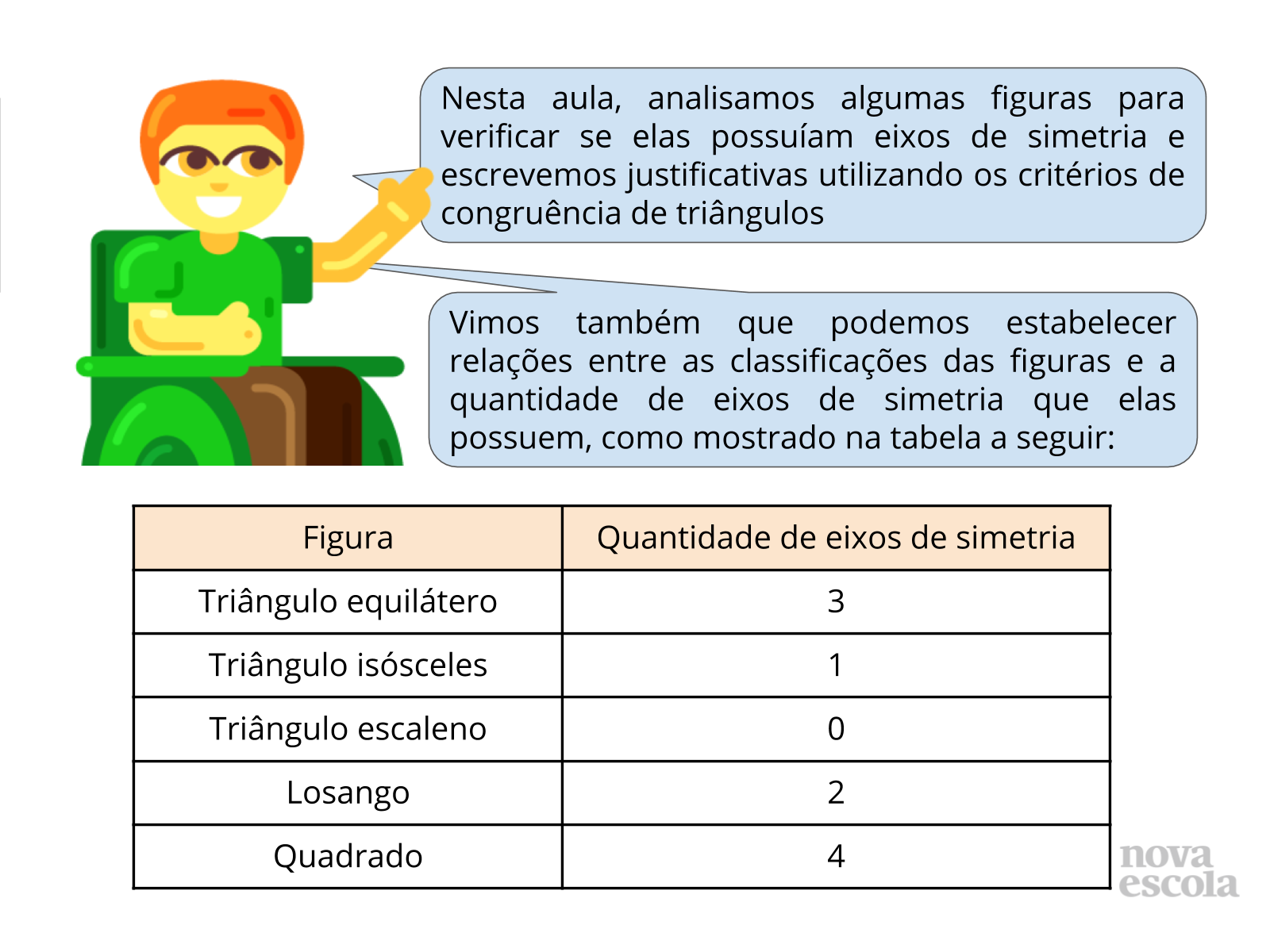
Orientações: Projete e leia o texto desse slide (ou apenas leia, caso o recurso da projeção não esteja disponível) para sistematizar as aprendizagens da aula. Peça para que os alunos registrem a conclusão sobre a quantidade de eixos de simetria nos triângulos e quadriláteros em seus cadernos (faça a tabela na lousa se não for possível projetar).
Propósito: Retomar as aprendizagens da aula, destacando o uso dos critérios de congruência na elaboração de justificativas e as relações entre as classificações das figuras e a quantidade de eixos de simetria que possuem .
Raio X
Tempo sugerido: 8 minutos
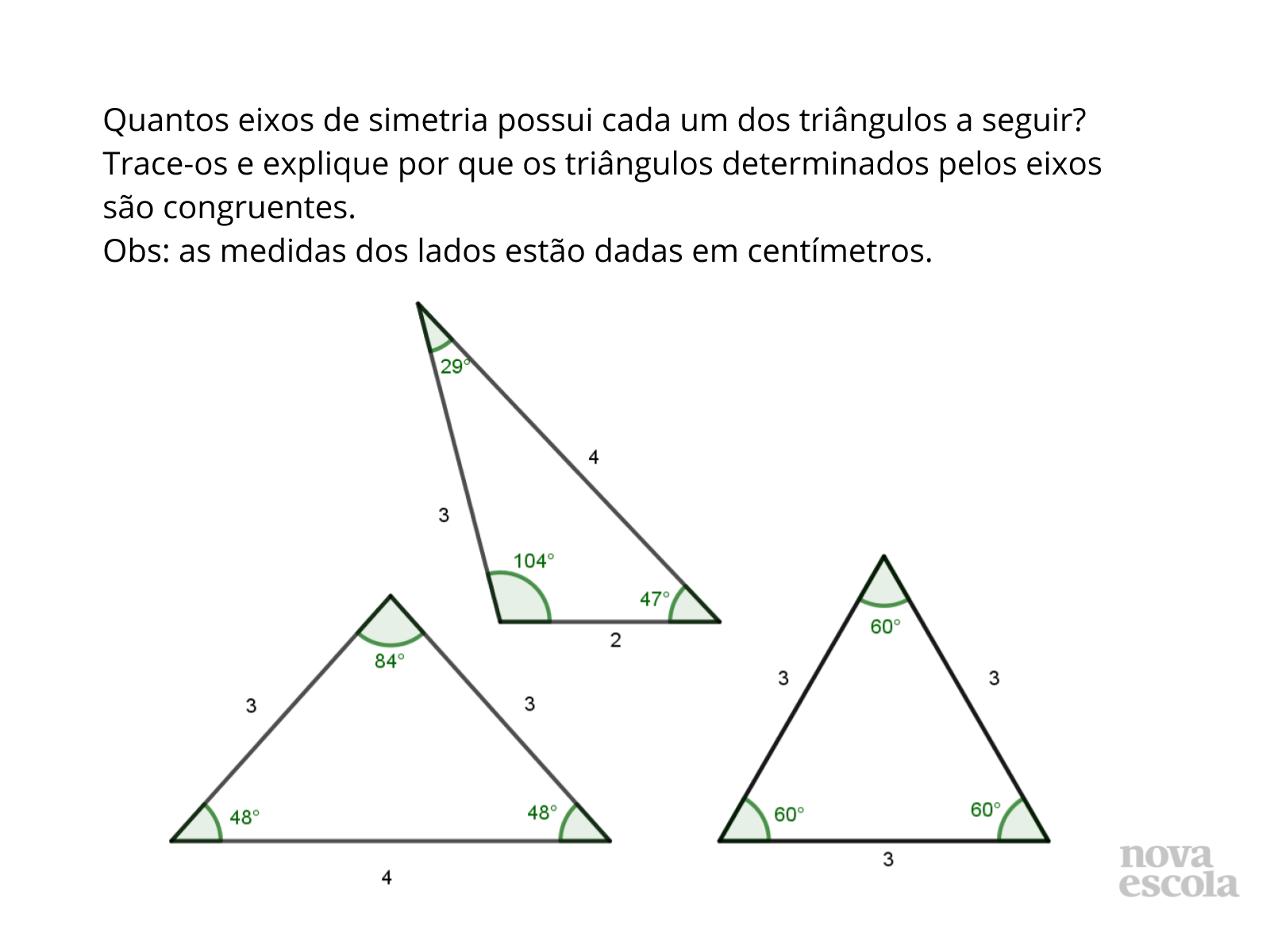
Orientações: Projete a atividade ou entregue cópias para os alunos e peça que, individualmente, leiam o enunciado e a realizem a atividade. Circule pela classe para verificar como os alunos estão realizando a tarefa e, caso algum aluno termine, solicite que ele determine, se possível, os valores de lados e ângulos das figuras congruentes obtidas. O raio X é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito da identificação de eixos de simetria e uso de critérios de congruência de triângulos para elaborar justificativas.
Materiais complementares para impressão:
Raio X
Sugestão de adaptação para ensino remoto
Código do plano
MAT8_15GEO09
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS
- Necessários: Papel, lápis, papel quadriculado, régua,WhatsApp
- Opcionais: Messenger Sala de aluno ( https://www.messenger.com/groupcall/LINK:4svjhs7dyZw8zoxm/), Meet, Hangout, Zoom, plataforma da Khan Academy ( https://pt.khanacademy.org/)
Portal OBMEP ( https://portaldaobmep.impa.br/index.php/modulo/lista?serie=3)
Geogebra https://play.google.com/store/apps/details?id=org.geogebra&hl=pt_BR
Para este plano, foque na etapa ATIVIDADE PRINCIPAL
Aquecimento
Use o Aquecimento nas orientações da realização da Atividade principal e solicite que os alunos elaborem um texto conclusivo sobre o tema.
Atividade principal
Sugerimos que você use o Aquecimento como apoio à orientação para realização da atividade pelos alunos. Encaminhe um áudio ou vídeo curto (WhatsApp) propondo a Atividade principal. Use a versão impressa e solicite o retorno das respostas para sua apreciação (inclusive do texto conclusivo sugerido no aquecimento). Nessa atividade é importante o uso de papel quadriculado, lápis e régua (reforce essa questão nas orientações). Caso seu aluno não tenha papel quadriculado, ele pode adaptar traçando verticalmente linhas numa folha de caderno, por exemplo. Mantenha um canal de comunicação com a turma.
Na plataforma da Khan Academy há vários vídeos e demais recursos que tratam de construção/congruência de triângulos e simetria. Você pode selecionar os materiais pertinentes e indicar aos alunos que possuem acesso à internet.
( https://pt.khanacademy.org/math/geometry/hs-geo-congruence/hs-geo-triangle-congruence/v/congruent-triangles-and-sss)
https://pt.khanacademy.org/math/pt-7-ano/geometria-angulos-e-polgonos-7ano/construcao-de-poligonos-regulares/v/construo-de-tringulo
https://pt.khanacademy.org/math/basic-geo/basic-geometry-shapes/basic-geo-classifying-triangles/v/constructing-triangles-with-constraints
https://pt.khanacademy.org/math/basic-geo/basic-geo-transformations-congruence/line-of-symmetry/v/identifying-symmetrical-figures
No Portal da OBMEP há exploração dos elementos básicos da geometria plana (partes 1, 2 e 3) que pode servir de apoio aos alunos que possuem internet.
https://portaldaobmep.impa.br/index.php/modulo/lista?serie
Discussão das soluções
Analise as respostas e as dúvidas apresentadas pelos alunos para compor um áudio ou vídeo (WhatsApp) com feedback aos alunos. Você pode usar dados da do painel de soluções e também do Encerramento nessa discussão. Verifique se há a necessidade de novas discussões. Talvez você precise elaborar um registro escrito para a turma com os principais conceitos e exemplos. Você pode considerar também as produções deles realizadas na atividade sugerida do Aquecimento. Se sua turma dispuser de ferramentas e internet, dê preferência por realizar as discussões em tempo real, por meio de uma das plataformas sugeridas abaixo. Se não tiver, use o WhatsApp que tem um alcance maior. Mas, não esqueça de manter um canal de comunicação para discussão também de sugerir a realização das demais atividades desse plano (atividades complementares e Raio X)
Se for possível discutir em tempo real, com sua turma, use o Meet, Hangout ou Zoom e considere apenas os itens e os conceitos de maior relevância.
Você pode usar também o Messenger Sala de aluno https://www.messenger.com/groupcall/LINK:4svjhs7dyZw8zoxm/
Sistematização
xxxx
Encerramento
Use nas discussões e/ou nas orientações iniciais
Raio X
Use o Raio X e as atividades complementares como forma de revisão para consolidação das aprendizagens. Não esqueça de retomar discussões também dessas atividades e focar nos pontos de aprendizagem mais críticos.
Convite às famílias
A atividade do Aquecimento pode ser discutida com as famílias
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Renata Akemi Maekawa
Mentor: Fabricio Eduardo Ferreira
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
EF08MA12 - Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
EF08MA15 - Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.
Objetivos específicos
-Reconhecer e traçar eixos de simetria de figuras
-Utilizar critérios de congruência de triângulos para justificar que uma reta é um eixo de simetria.
-Relacionar as classificações dos triângulos quanto aos lados ao número de eixos de simetria que a figura possui.
Conceito-chave
Simetrias e congruência de triângulos.
Recursos necessários
-Fichas impressas.
-Projetor (se possível)















