Resumo da aula
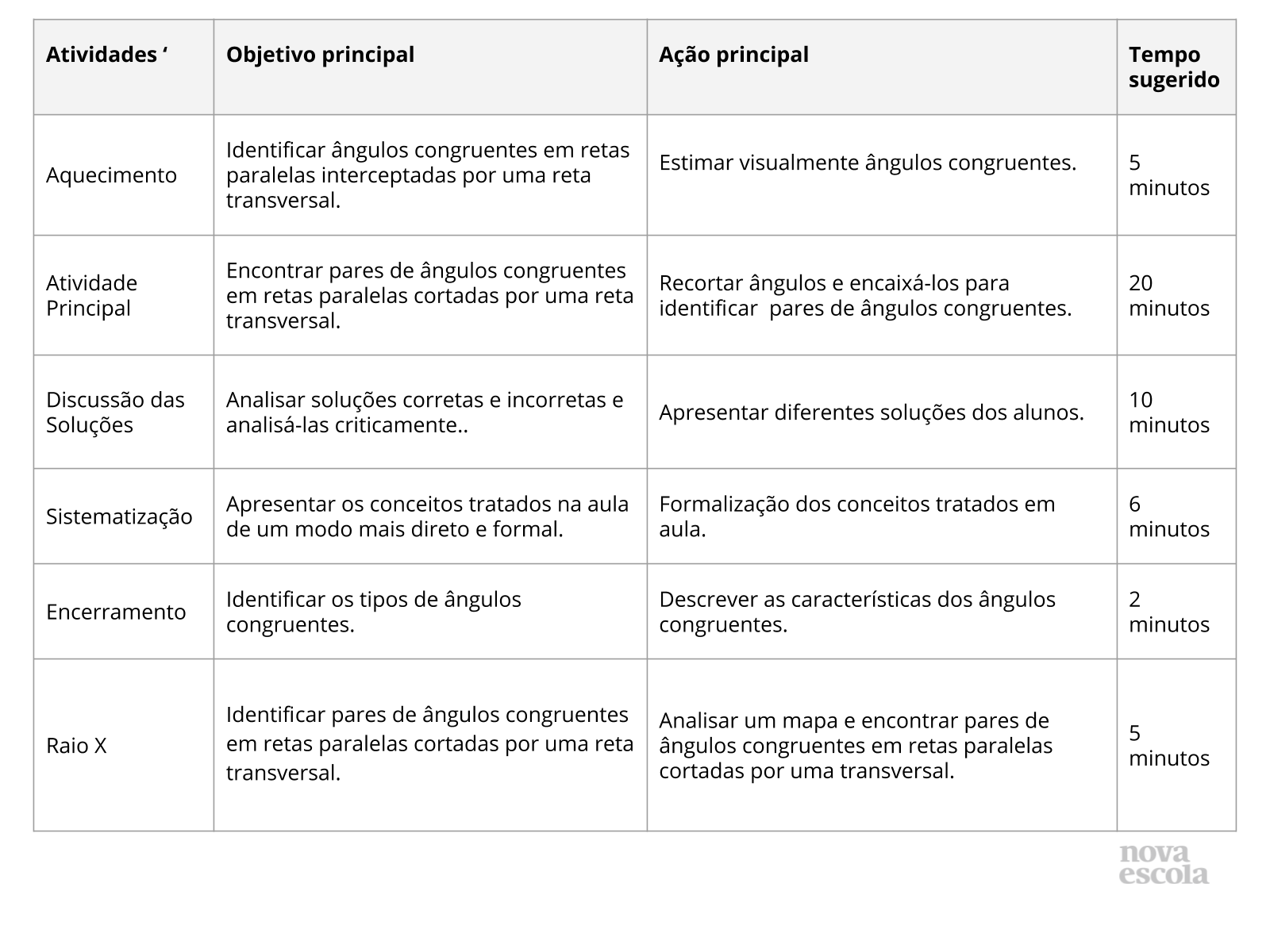
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos
Orientação: Mostre o slide, leia ou escreva na lousa o objetivo da aula. Isso faz com que a aula tenha mais sentido para eles e fará com que percebam que você tem um objetivo com esta aula.
Propósito: Partilhar o objetivo com os alunos contribui para que eles fiquem em prontidão para a aula.
Aquecimento

Tempo sugerido: 5 minutos (Tempo total: slides 3 e 4)
Orientação: Verifique se os alunos sabem claramente o que é um ângulo e o que são ângulos congruentes.Faça uma pequena discussão com a sala toda. Deixe que eles falem e, em seguida, aproveite para refinar as ideias a respeito da congruência explicando que ângulos congruentes são ângulos que possuem a mesma medida. Além disso, é interessante destacar que o termo “ângulos iguais” seria usado se fosse o mesmo ângulo. Aqui estamos trabalhando com ângulos diferentes mas que possuem a mesma medida. Desenhe na lousa algumas retas paralelas cortadas por uma reta transversal, porque essa frase pode não fazer sentido para eles.
Essa atividade pode ser feita em duplas. Oriente-os a observar a abertura de cada ângulo para tentar identificar quais tem a mesma medida (a mesma abertura). Oriente-os a fazer a atividade sem utilizar transferidor pois trata-se de uma atividade visual.
Propósito: Verificar brevemente os conhecimentos prévios dos alunos a respeito dos termos que serão tratados.
Discuta com a turma:
- Quantos pares de ângulos congruentes você consegue formar?
- Dentre dois ângulos (escolha dois quaisquer), você consegue dizer qual é o maior?
Aquecimento
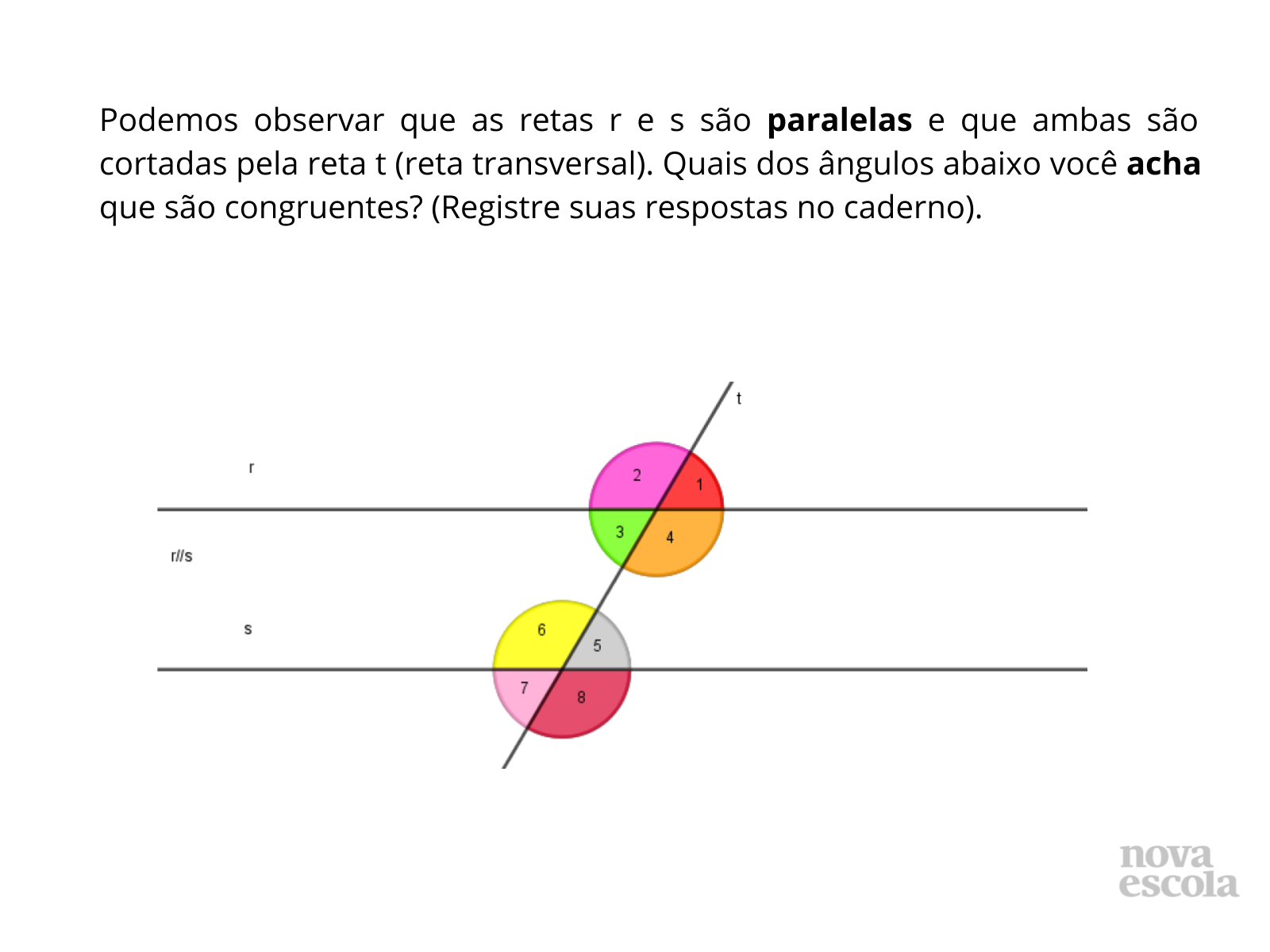
Tempo sugerido: 5 minutos (Tempo total: slides 3 e 4)
Orientação: Verifique se os alunos sabem claramente o que é um ângulo e o que são ângulos congruentes.Faça uma pequena discussão com a sala toda. Deixe que eles falem e, em seguida, aproveite para refinar as ideias a respeito da congruência explicando que ângulos congruentes são ângulos que possuem a mesma medida. Além disso, é interessante destacar que o termo “ângulos iguais” seria usado se fosse o mesmo ângulo. Aqui estamos trabalhando com ângulos diferentes mas que possuem a mesma medida. Desenhe na lousa algumas retas paralelas cortadas por uma reta transversal, porque essa frase pode não fazer sentido para eles.
Essa atividade pode ser feita em duplas. Oriente-os a observar a abertura de cada ângulo para tentar identificar quais tem a mesma medida (a mesma abertura). Oriente-os a fazer a atividade sem utilizar transferidor pois trata-se de uma atividade visual.
Propósito: Verificar brevemente os conhecimentos prévios dos alunos a respeito dos termos que serão tratados.
Discuta com a turma:
- Quantos pares de ângulos congruentes você consegue formar?
- Dentre dois ângulos (escolha dois quaisquer), você consegue dizer qual é o maior?
Atividade principal
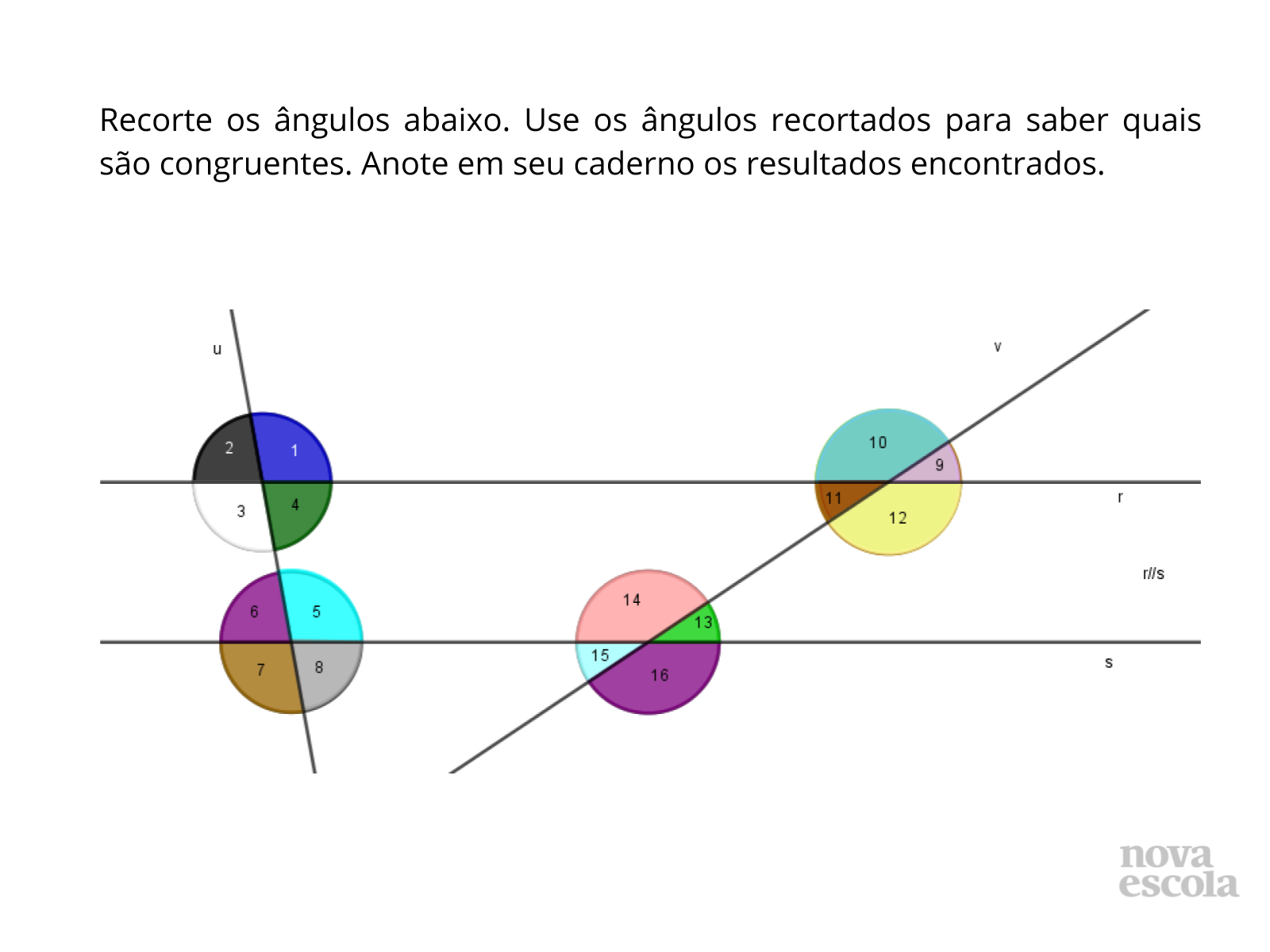
Tempo sugerido: 20 minutos (slides de 5 e 6).
Orientação: Os alunos agora deverão comparar os ângulos e verificar quais são congruentes. Para tanto basta sobrepor um ao outro. Deixe que percebam isso sozinhos.
Propósito: Fazer com que os alunos percebam a congruência entre ângulos de forma mais concreta para facilitar o entendimento.
Discuta com a turma:
- Olhando para os ângulos recortados por vocês, como eu vou saber se são iguais ou diferentes?
- Quantos ângulos diferentes você pode observar em cada transversal?
Atividade Principal
Resolução da Atividade Principal
Guia de Intervenção
Atividade principal
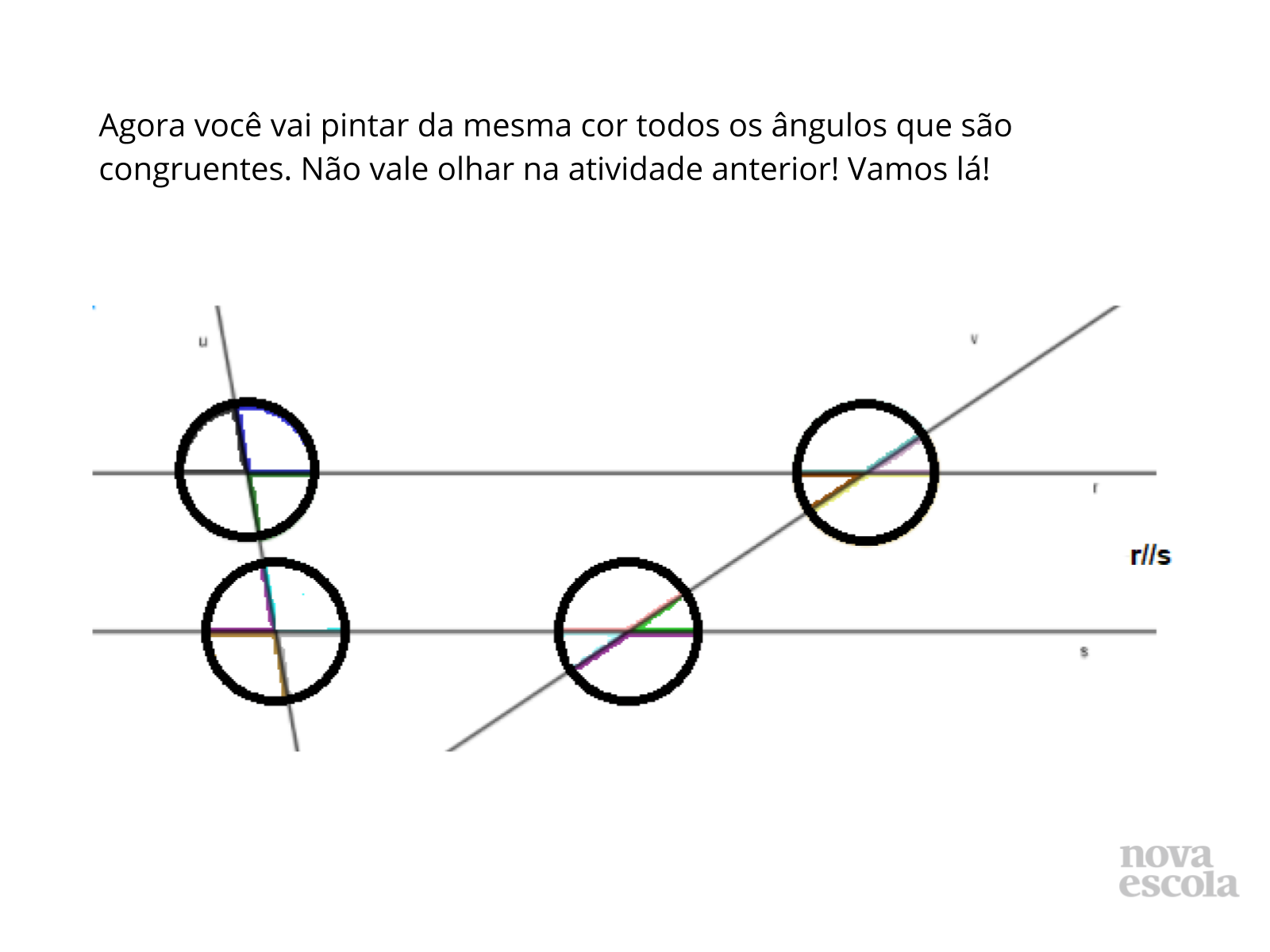
Tempo sugerido: 20 minutos (slides de 5 e 6).
Orientação: Os alunos agora deverão comparar os ângulos e verificar quais são congruentes. Para tanto basta sobrepor um ao outro. Deixe que percebam isso sozinhos.
Propósito: Fazer com que os alunos percebam a congruência entre ângulos de forma mais concreta para facilitar o entendimento.
Discuta com a turma:
- Olhando para os ângulos recortados por vocês, como eu vou saber se são iguais ou diferentes?
- Quantos ângulos diferentes você pode observar em cada transversal?
Discutindo as soluções

Tempo sugerido: 10 minutos (slides 9 e 10).
Orientação: Procure apresentar as soluções dos alunos. Pode pedir a eles mesmos que apresentem na frente da sala. Caso não encontre muitos erros diferentes aqui estão duas soluções incorretas e uma correta.
- O garoto considerou os ângulos opostos pelo vértice (não estamos usando a nomenclatura ainda) congruentes, mas não percebeu que os ângulos correspondentes também são congruentes.
- A menina de pé não compreendeu o conceito de congruência. Ela considera que os ângulos complementares são congruentes.
- A menina agachada compreendeu o conceito e respondeu corretamente.
Propósito: Analisar respostas diferentes. Perceber os diferentes caminhos que podemos utilizar para resolver uma questão matemática.
Discuta com a turma:
- O que vocês conseguem perceber sobre os ângulos nesta atividade?
- Se eu comparar a primeira reta transversal com a segunda, o que elas tem de diferente? E o que
Discutindo as soluções
Tempo sugerido: 10 minutos (slides 9 e 10).
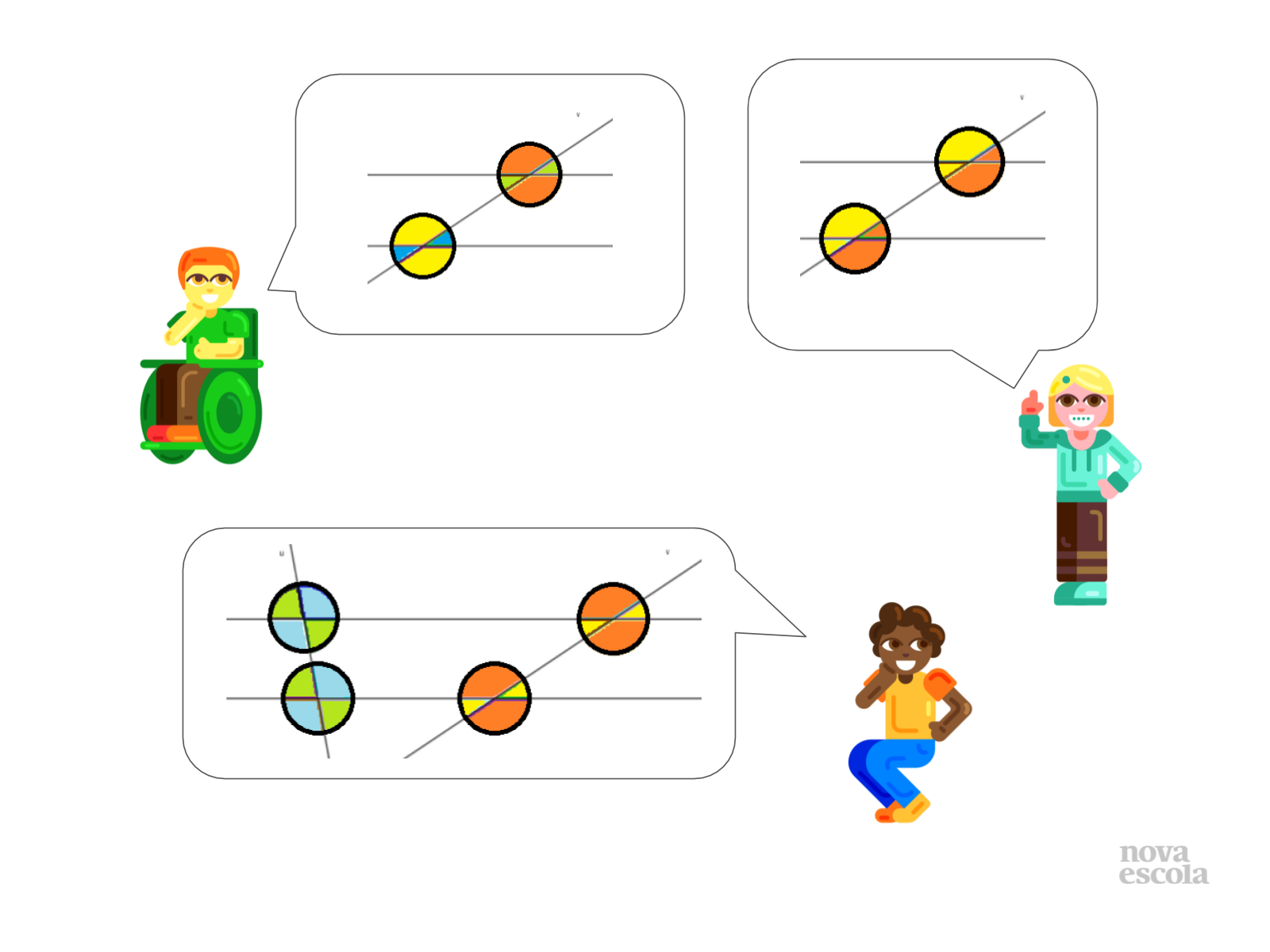
Orientação: Procure apresentar as soluções dos alunos. Pode pedir a eles mesmos que apresentem na frente da sala. Caso não encontre muitos erros diferentes aqui estão duas soluções incorretas e uma correta.
- O garoto considerou os ângulos opostos pelo vértice (não estamos usando a nomenclatura ainda) congruentes, mas não percebeu que os ângulos correspondentes também são congruentes.
- A menina de pé não compreendeu o conceito de congruência. Ela considera que os ângulos complementares são congruentes.
- A menina agachada compreendeu o conceito e respondeu corretamente.
Propósito: Analisar respostas diferentes. Perceber os diferentes caminhos que podemos utilizar para resolver uma questão matemática.
Discuta com a turma:
- O que vocês conseguem perceber sobre os ângulos nesta atividade?
- Se eu comparar a primeira reta transversal com a segunda, o que elas tem de diferente? E o que
Vamos formalizar o que já vimos
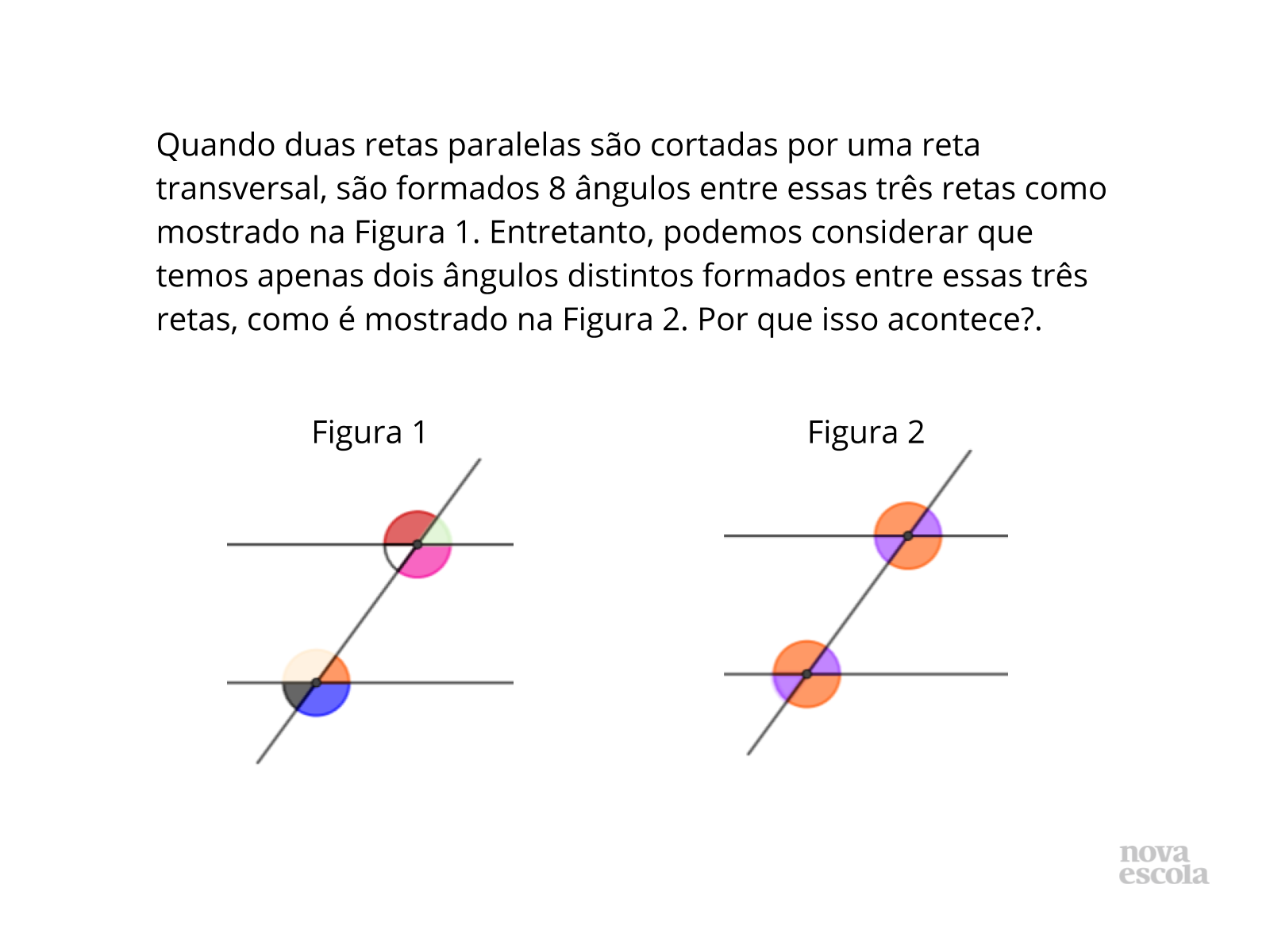
Tempo sugerido: 6 minutos (slides 9 e 10).
Orientação: Você pode mostrar os slides ou passar na lousa o conteúdo sistematizado do tema tratado nesta aula. Os alunos deverão copiar este conteúdo no caderno. É importante, neste momento, utilizar um vocabulário formal com os conceitos tratados corretamente. Procure indicar para os alunos (isso durante toda a aula) que nós podemos nos referir de forma mais livre aos objetos matemáticos quando estamos aprendendo a sua funcionalidade, mas que, depois dessa fase, temos que nos esforçar para usar os conceitos tratados corretamente e utilizar a nomenclatura correta porque, em Matemática, a precisão tanto de conceitos como de nomenclatura faz muita diferença.
Propósito: A formalização é um momento importante da aula, pois dá uma visão geral e mais clara do que foi tratado em aula e apresenta os conceitos e nomenclaturas corretamente.
Vamos formalizar o que já vimos
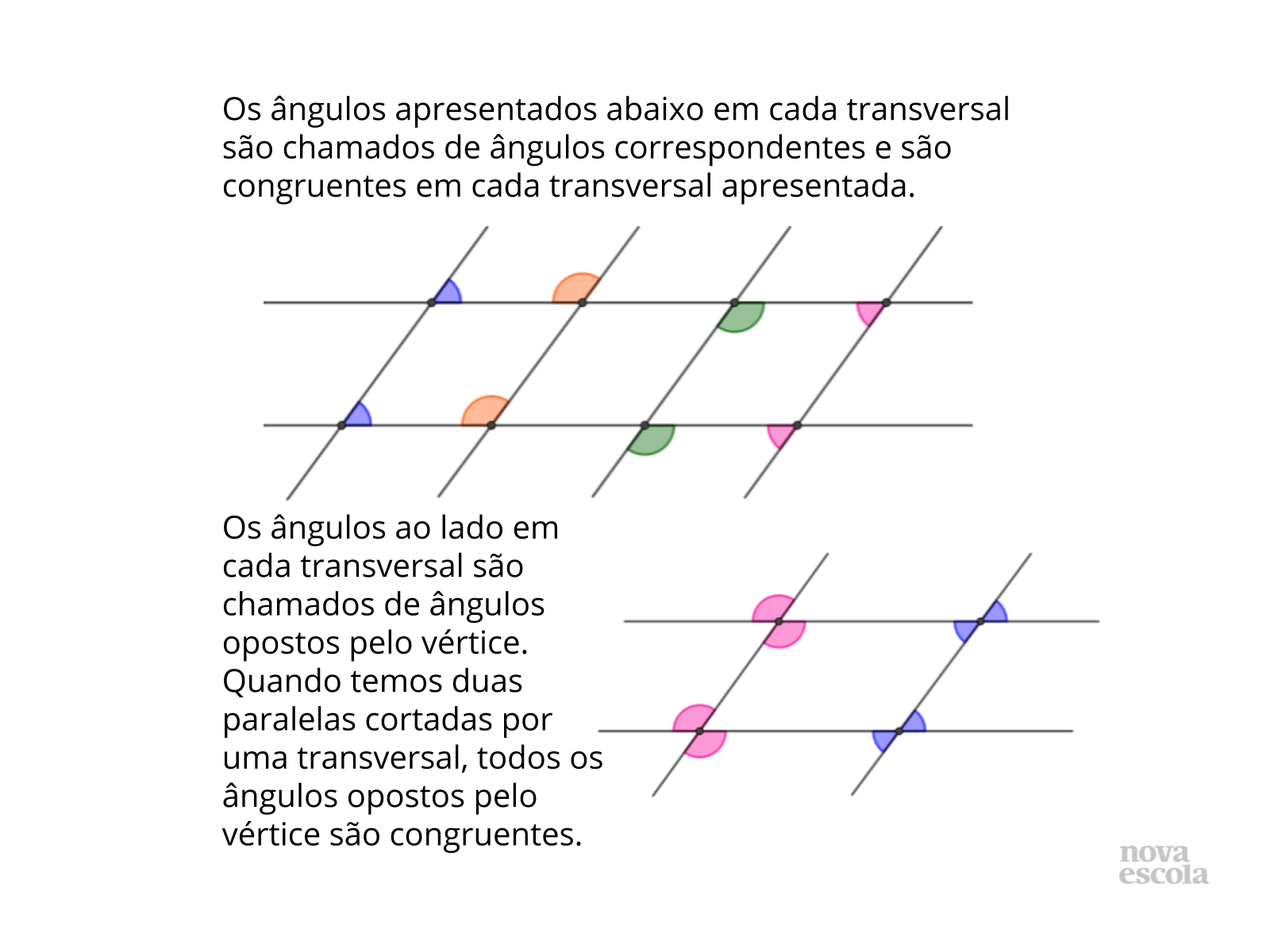
Tempo sugerido: 6 minutos (slides 9 e 10).
Orientação: Você pode mostrar os slides ou passar na lousa o conteúdo sistematizado do tema tratado nesta aula. Os alunos deverão copiar este conteúdo no caderno. É importante, neste momento, utilizar um vocabulário formal com os conceitos tratados corretamente. Procure indicar para os alunos (isso durante toda a aula) que nós podemos nos referir de forma mais livre aos objetos matemáticos quando estamos aprendendo a sua funcionalidade, mas que, depois dessa fase, temos que nos esforçar para usar os conceitos tratados corretamente e utilizar a nomenclatura correta porque, em Matemática, a precisão tanto de conceitos como de nomenclatura faz muita diferença.
Propósito: A formalização é um momento importante da aula, pois dá uma visão geral e mais clara do que foi tratado em aula e apresenta os conceitos e nomenclaturas corretamente.
Encerrando

Tempo sugerido: 2 minutos.
Orientação: Você pode apresentar o encerramento com o slide, ler para a sala ou escrever na lousa. O objetivo, como o nome indica, é dar um fechamento para a aula.
Propósito: Dar ao aluno uma visão geral do que foi tratado na aula e dar uma sensação de fechamento.
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. 





















