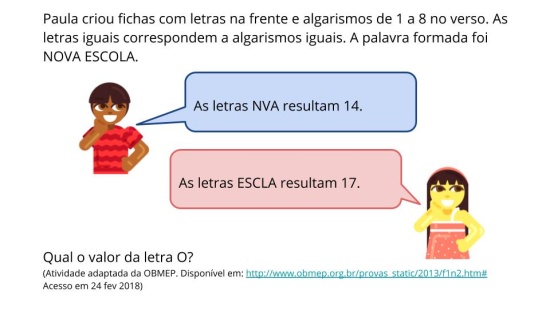
Aquecimento
Plano de Aula
Plano de aula: Ampliação - Resolver problema de investigação
Plano 6 de uma sequência de 10 planos. Veja todos os planos sobre Resolução de problemas
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Érica Fernanda Barbosa dos Santos.
Mentor: Tatiane Cristina Guadagnucci.
Especialista de área: Rita Batista.
Habilidade da BNCC
NÃO HÁ.
Objetivos específicos
Estimular a compreensão de que resolver problema é um processo de investigação para transformar a linguagem usual em representação matemática, estimular o aluno a ser protagonista da sua aprendizagem e gerenciar seus erros e acertos.
Conceito-chave
Problemas de investigação, regularidades.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não.
Habilidades BNCC:
Objetivos de aprendizagem
Estimular a compreensão de que resolver problema é um processo de investigação para transformar a linguagem usual em representação matemática, estimular o aluno a ser protagonista da sua aprendizagem e gerenciar seus erros e acertos.
Resumo da aula
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula para que os alunos saibam a intencionalidade que se pretende desenvolver na aula.
Retomada
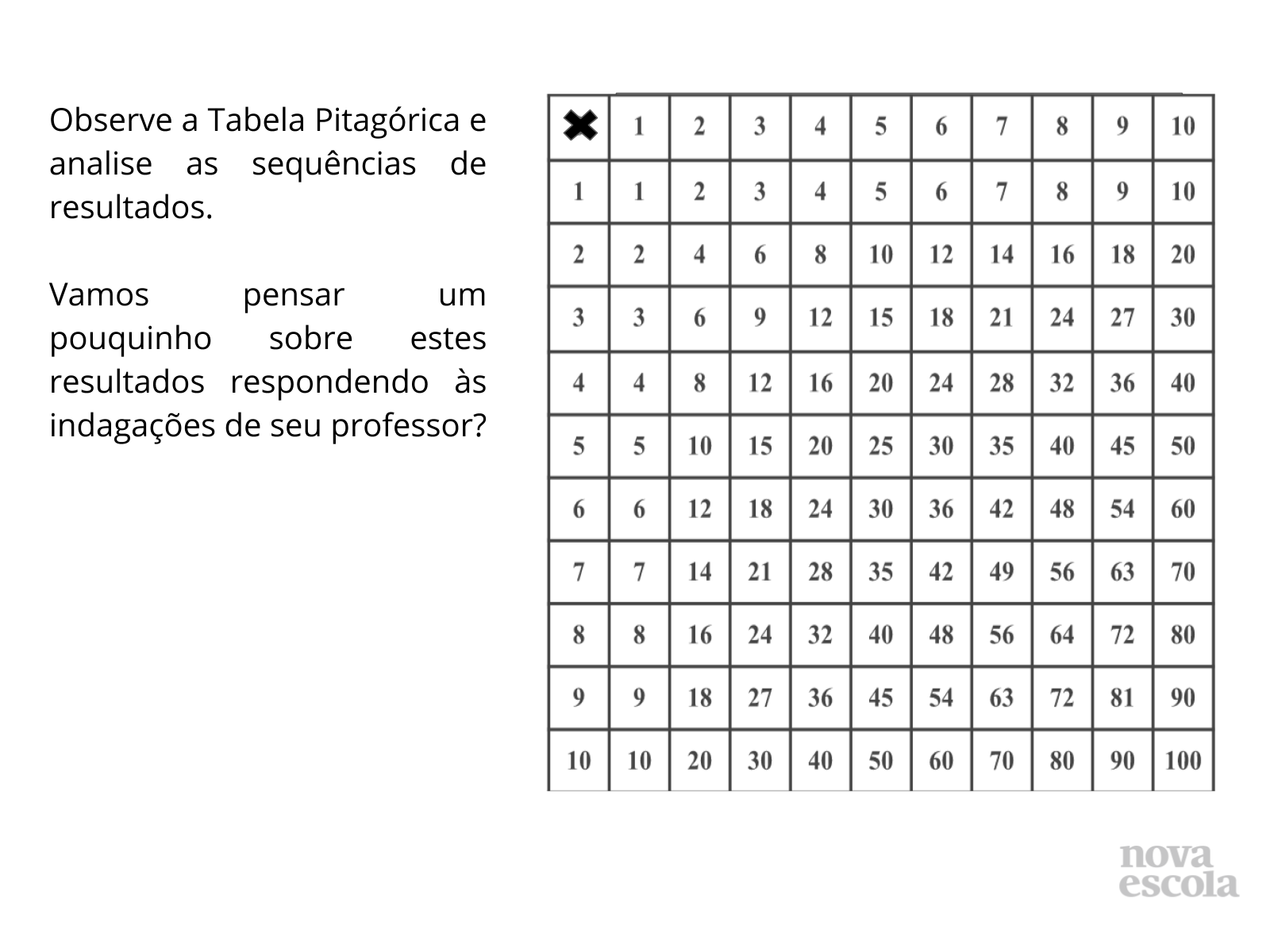
Tempo sugerido: 7 minutos.
Orientação: Projete a atividade na lousa ou entregue uma cópia para cada aluno, peça para os alunos individualmente analisar a sequência dos múltiplos. Questione os alunos considerando as perguntas presentes no DISCUTA COM A TURMA.
- É possível notar que os múltiplos de 10 são o dobro dos múltiplos de 5; assim como os múltiplos de 8 são o dobro dos múltiplos de 4 e ainda o quádruplo dos múltiplos de 2; os múltiplos de 6 são o dobro dos múltiplos de 3; os múltiplos de 9 são o triplo dos múltiplos de 3;
- Os múltiplos de 2 são metade dos múltiplos de 4 e a quarta parte dos múltiplos de 8; os múltiplos de 3 são a metade dos múltiplos de 6 e a terça parte dos múltiplos de 9; os múltiplos de 5 são a metade dos múltiplos de 10.
- É possível explorar a propriedade distributiva ao perceber que a soma da sequência de múltiplos de dois algarismos distintos, resulta na sequência de múltiplos de um terceiro algarismo, por exemplo, para saber o valor de 15×4, faça o seguinte: (10+5)×4 = 10×4+5×4 = 40+20 = 60, ou, 15×4=(20 - 5)×4 = 20×4-5×4 = 80-20 = 60;
Este último “exercício” promove uma familiaridade com a propriedade distributiva que auxilia na aprendizagem de multiplicação de monômios e polinômios.
Material complementar
Propósito: Promover a familiaridade com problemas de investigação.
Discuta com a turma:
- Quais elementos interessantes você observa considerando os resultados e as relações entre eles?
- Como se relacionam, por exemplo, os múltiplos de de 5 com os múltiplos de 10?
- Você observa alguma particularidade nos resultados das diagonais? (Veja a diagonal que vai de x até 100 e a que vai de 10 até 10)
- Qual o número central da tabela? Por que você acha é exatamente este número o que fica bem no meio da tabela?
- Descreva um erro ou conceito errôneo que você ou um colega apresentou na realização da atividade? O que você aprendeu com esse conceito errôneo?
Recomendações de leituras:
Um pouco de história: A Tabela Pitagórica foi criada pelo filósofo grego e matemático Pitágoras no século VI a. C. É formada por uma tabela de dupla entrada em que na primeira linha e na primeira coluna contém números de 1 a 10. Os números das linhas são multiplicados pelos números das colunas e vice-versa.
A Tabela Pitagórica promove uma visão geral da tabuada e “favorece a análise de regularidade apoiadas nas propriedades comutativa, distributiva, associativa e na reconstrução de resultados” (Claudia Broitman, 2011. Disponível em: https://novaescola.org.br/conteudo/3841/tabuada-como-usar-a-tabela-pitagorica )
Atividade principal

Tempo sugerido: 17 minutos (slides 4 e 5).
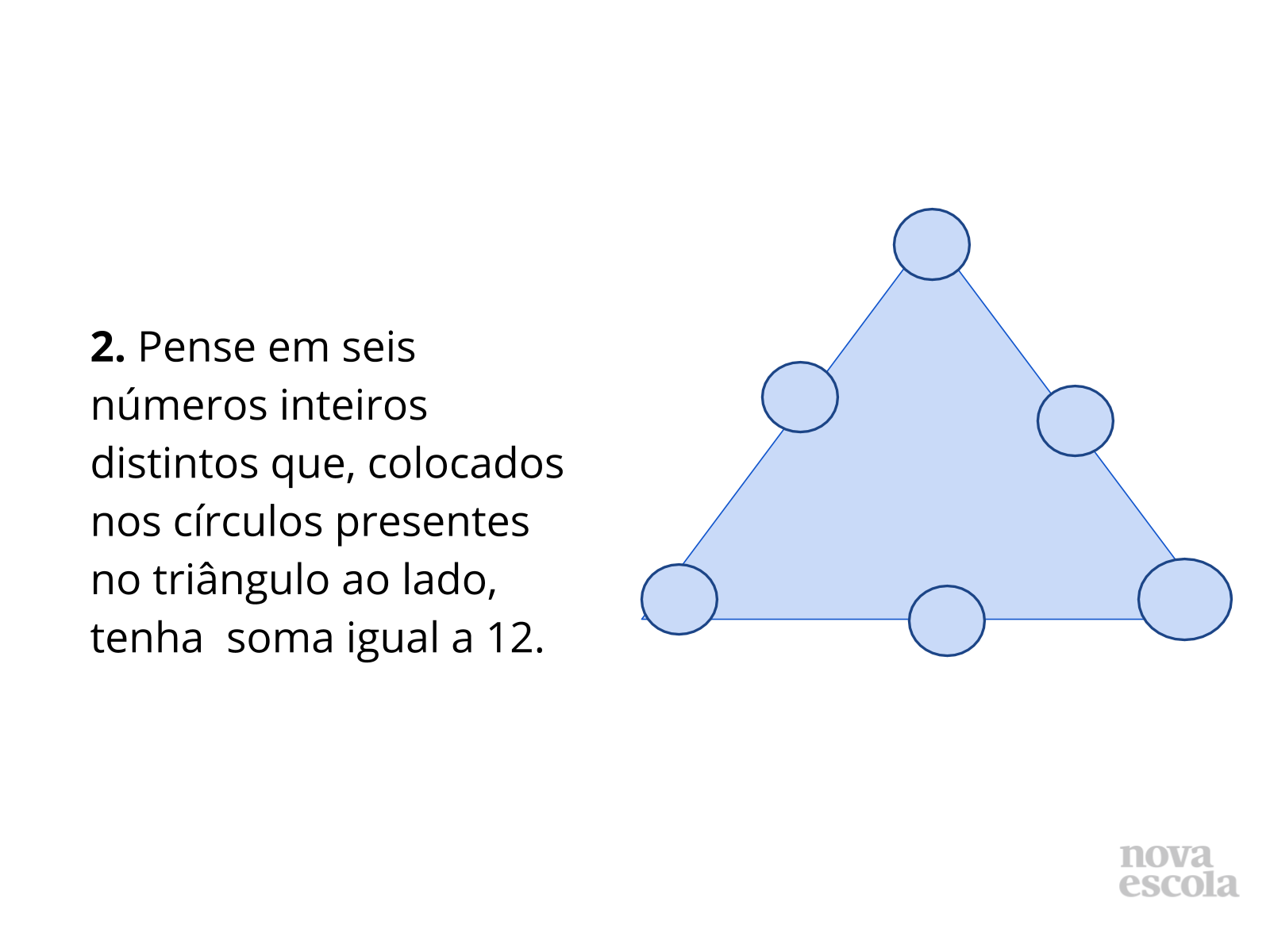
Orientações: Entregue a atividade impressa, ou projete na lousa para que os alunos possam copiar o triângulo. Peça para os alunos resolvam em duplas as duas situações propostas nesta atividade.
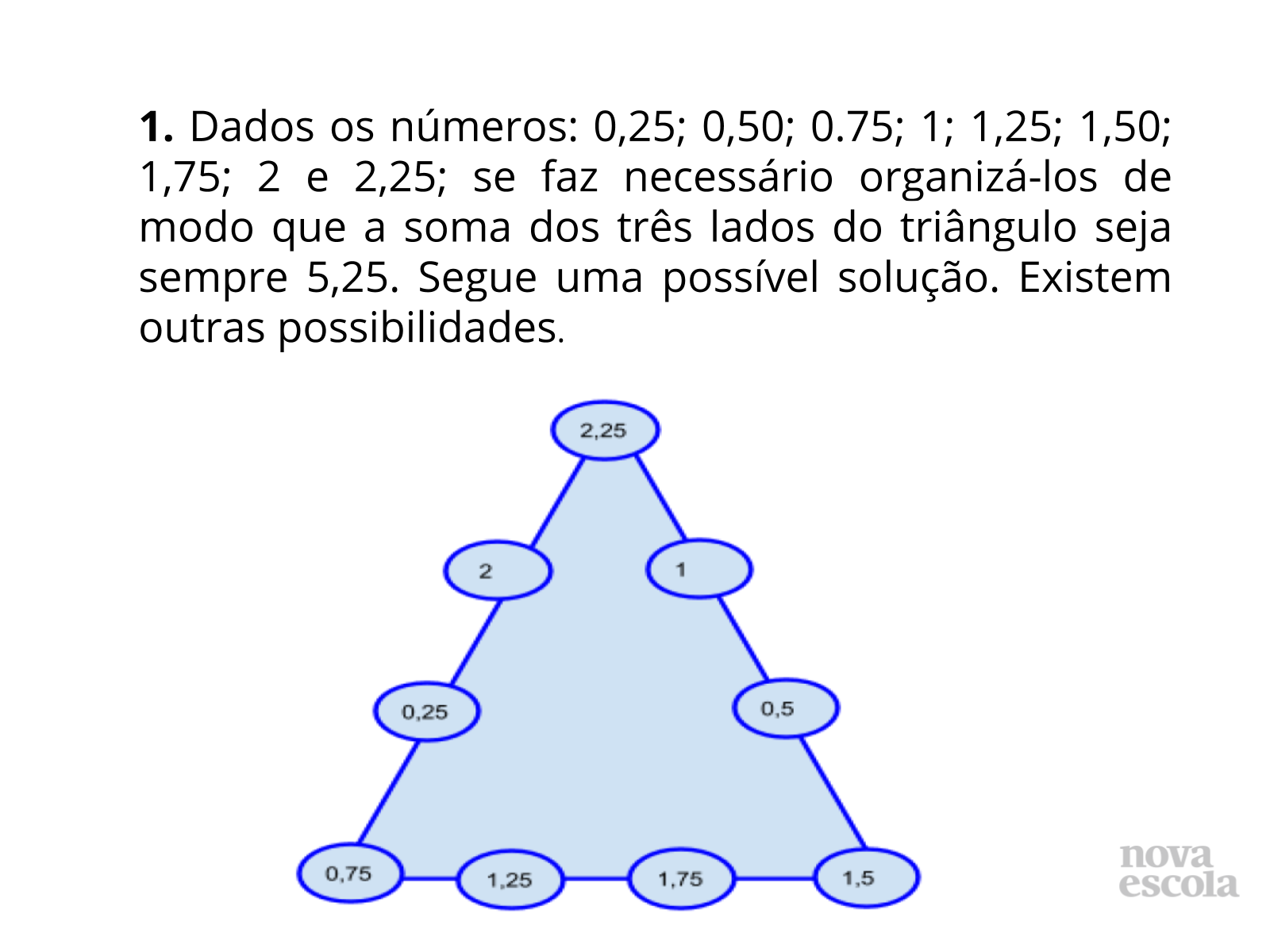
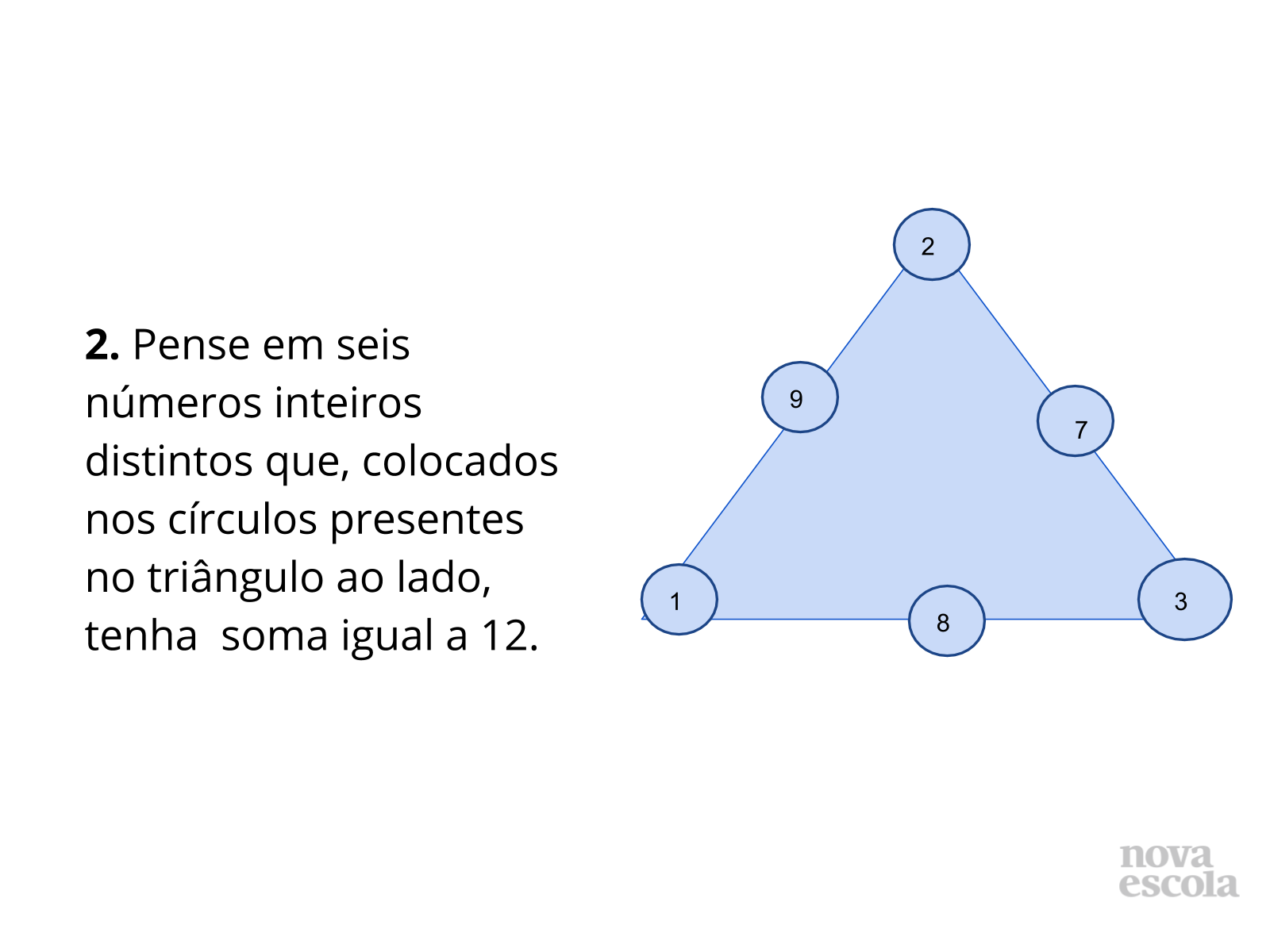
A primeira cujo o intuito é que os alunos completem os círculos dos triângulos de modo que a soma de todas as linhas seja sempre 5,25 e a segunda onde eles terão que fazer um caminho inverso (mais ampliado) que poderá ser facilitado por se tratar de números inteiros, apesar que eles podem pensar também em números reais.
Em seguida, promova uma discussão entre as duplas para argumentarem sobres suas soluções. O objetivo do problema de investigação é estimular o aluno a buscar informações que aprimore o conhecimento já adquirido. Na realização da atividade os alunos se tornam responsáveis por suas descobertas, assim como por argumentar sobre a solução apresentada. É muito importante não dar respostas, e sim estimular os alunos a realizar o esforço produtivo e representar suas ideias por meio de símbolos (desenho, esquemas ou tabelas).
A última pergunta do DISCUTA COM A TURMA, permite que os alunos reflitam sobre um possível equívoco caso não considerem os números presentes vértices como pontos comuns dos lados do triângulo na situação apresentada.
Utilize o guia de intervenção para discutir com os alunos as formas e possibilidades de representação da solução.
Propósito: Desenvolver o raciocínio lógico e dedutivo.
Discuta com a turma:
- Quais são os dados que o problema apresenta?
- Considerando os dados do problema, alguém se lembra de ter resolvido algum problema parecido?
- Alguém tem alguma estratégia para resolver o problema?
- Como você ou seu grupo abordou o problema ou conjunto de problemas de hoje? Sua abordagem foi bem sucedida? O que você aprendeu com sua abordagem?
- Você acha que o 0,50 do problema poderia ser substituído pelo 0,5 sem mudança no resultado?
- O que aconteceria com o resultado
- O resultado da soma de todos os números dados totaliza 11,25. Queremos organizar os números para cada lado resultar em 5,25. Como isso é possível em cada um dos lados do triângulo? A soma total de todos os números não deveria ser 15,75 (5,25 x 3)? Como você justifica isto?
Disponível em: https://www.google.com/url?q=http://clubes.obmep.org.br/blog/problema-triangulo-magico/&sa=D&ust=1516212504948000&usg=AFQjCNEC5OW0KlCNAzyB4fs6UmNOu_VK1Q . Acesso em 17 jan 2018)
Atividade principal
Tempo sugerido: 17 minutos (slides 4 e 5).
Orientações: Entregue a atividade impressa, ou projete na lousa para que os alunos possam copiar o triângulo. Peça para os alunos resolvam em duplas as duas situações propostas nesta atividade.
A primeira cujo o intuito é que os alunos completem os círculos dos triângulos de modo que a soma de todas as linhas seja sempre 5,25 e a segunda onde eles terão que fazer um caminho inverso (mais ampliado) que poderá ser facilitado por se tratar de números inteiros, apesar que eles podem pensar também em números reais.
Em seguida, promova uma discussão entre as duplas para argumentarem sobres suas soluções. O objetivo do problema de investigação é estimular o aluno a buscar informações que aprimore o conhecimento já adquirido. Na realização da atividade os alunos se tornam responsáveis por suas descobertas, assim como por argumentar sobre a solução apresentada. É muito importante não dar respostas, e sim estimular os alunos a realizar o esforço produtivo e representar suas ideias por meio de símbolos (desenho, esquemas ou tabelas).
A última pergunta do DISCUTA COM A TURMA, permite que os alunos reflitam sobre um possível equívoco caso não considerem os números presentes vértices como pontos comuns dos lados do triângulo na situação apresentada.
Utilize o guia de intervenção para discutir com os alunos as formas e possibilidades de representação da solução.
Propósito: Desenvolver o raciocínio lógico e dedutivo.
Discuta com a turma:
- Quais são os dados que o problema apresenta?
- Considerando os dados do problema, alguém se lembra de ter resolvido algum problema parecido?
- Alguém tem alguma estratégia para resolver o problema?
- Como você ou seu grupo abordou o problema ou conjunto de problemas de hoje? Sua abordagem foi bem sucedida? O que você aprendeu com sua abordagem?
- Você acha que o 0,50 do problema poderia ser substituído pelo 0,5 sem mudança no resultado?
- O que aconteceria com o resultado
- O resultado da soma de todos os números dados totaliza 11,25. Queremos organizar os números para cada lado resultar em 5,25. Como isso é possível em cada um dos lados do triângulo? A soma total de todos os números não deveria ser 15,75 (5,25 x 3)? Como você justifica isto?
Disponível em: https://www.google.com/url?q=http://clubes.obmep.org.br/blog/problema-triangulo-magico/&sa=D&ust=1516212504948000&usg=AFQjCNEC5OW0KlCNAzyB4fs6UmNOu_VK1Q . Acesso em 17 jan 2018)
Discussão da solução
Tempo sugerido: 12 minutos (slides 6 e 7).
Orientações: Peça que alguns grupos apresentem suas soluções. Incentive para que eles justifiquem suas escolhas e informem o que julgaram difícil ou fácil.
Propósito: Discutir soluções possíveis
Discuta com a turma:
- Você teve alguma dificuldade?
- Comunique a seus colegas como você pensou...
Painel de Solução
Tempo sugerido: 12 minutos (slides 6 e 7).
Orientações: Peça que alguns grupos apresentem suas soluções. Incentive para que eles justifiquem suas escolhas e informem o que julgaram difícil ou fácil.
Propósito: Discutir soluções possíveis
Discuta com a turma:
- Você teve alguma dificuldade?
- Comunique a seus colegas como você pensou…
- Há mais de uma solução?
- Você pensou em incluir números decimais?
- Seria possível se fosse incluído raiz quadrada? E fração?
Encerramento

Tempo sugerido: 2 minutos.
Orientações: Encerre a atividade retomando com os alunos a importância de entender a situação problema, reconhecer os dados que o problema fornece e a pergunta que tem que ser respondida. E ainda os conceitos necessários para representar a solução do problema.
Propósito: Sintetizar o conhecimento adquirido na aula.
Discuta com a turma:
- Quais foram os principais conceitos ou ideias matemáticas que você aprendeu hoje ou discutimos em aula hoje?
- Quais foram seus pontos fortes e fracos, nesta atividade? Qual é o seu plano para melhorar nas áreas em que teve dificuldades?
Raio x

Tempo sugerido: 10 minutos.
Orientação: Entregue aos alunos uma cópia da questão, para que individualmente analisem o problema proposto, e apresentem estratégias que satisfaçam a solução. O objetivo desta atividade é estimular o aluno a desenvolver seu pensamento matemático por meio da representação simbólica durante a apresentação das possíveis soluções para o problema, desenvolver no aluno habilidades para argumentar diante da hipótese de solução em defesa de seu ponto de vista de maneira autônoma. Um problema de investigação visa estimular o aluno a ser protagonista de seu conhecimento, o aluno tende a se deparar com um erro, neste momento o professor deve ser mediador da situação, estimulando a lidar com os erros e buscar alternativas para encontrar a solução
Propósito: Consolidar a aprendizagem de participação ativa na resolução de problemas de investigação.
Discuta com a turma:
- Qual a pergunta para o problema?
- Quais estratégias você pensou para explicar a solução do problema?
- Quais maneiras foram pensadas para descrever as soluções encontradas?
- Quais foram os principais conceitos ou ideias matemáticas que você aprendeu hoje ou que discutimos em aula hoje?
- Descreva um erro ou conceito errôneo que você ou um colega apresentou na aula de hoje. O que você aprendeu com esse erro ou conceito errôneo?
Para os alunos
Para o professor
Sugestão de adaptação para ensino remoto
Código do plano
MAT8_26RDP06
Recursos
- Necessários:
- caderno
- lápis
- grupo de alunos no WhatsApp
- Opcionais:
- Google Sala de Aula
- Meet
- Zoom
- Padlet
- Jamboard
Dicas de uso do Jamboard no link: https://support.google.com/jamboard/#topic=7383644
Para este plano, foque na etapa: Atividade Principal
Atividade Principal
Para a realização dessa atividade, o aluno precisa ter em mãos a situação-problema. Você pode enviar uma foto do problema via WhatsApp e montar um Painel de Soluções, com todos os dados do problema, utilizando o Padlet, o Jamboard, ou produzir um arquivo de forma que todos possam ter acesso. Peça para que, em duplas, os alunos discutam as possíveis soluções, registrem no caderno e, após analisarem, preencham os espaços indicados nos Triângulos, a interação entre eles pode ser feita via chamada de vídeo do WhatsApp. Instigue a argumentação e a comparação das soluções encontradas. Sugira os jogos online, “Soma 9 no triângulo” no link,
http://www.cercifaf.org.pt/mosaico.edu/ca/tsoma9.html, (acesso em 04 de jul 2020) e “Soma 10 no triângulo” no link http://www.cercifaf.org.pt/mosaico.edu/ca/tsoma10.html, (acesso em 04 de jul 2020).
Na primeira parte da atividade os alunos devem completar os círculos dos triângulos de modo que a soma dos valores de cada lado seja sempre 5,25 e na segunda parte eles terão que fazer um caminho inverso (mais ampliado), que poderá ser facilitado por se tratar de números inteiros. Estimule os alunos a realizar o esforço produtivo e representar suas ideias por meio desenho, esquemas ou algoritmos. Se o aluno apresentar dificuldades para resolver a Adição com números decimais, sugira que assista o vídeo "Soma de números decimais: 9,087+15,31"- Khan Academy, no link: https://youtu.be/i03fCG9k_bo (acesso em 04 de jul 2020). Solicite que anotem suas estratégias e respostas, para compartilhar com a turma.
Discussão das soluções
Professor, verifique as orientações feitas no Guia de Intervenção no link https://nova-escola-producao.s3.amazonaws.com/S7wugs9SJf2FWaYw9MDGQKfe4C6d6AFVj6eTb7b2JkWg8ha26P5ZbXnyUWAQ/guiainterv-mat8-26rdp06.pdf, elas serão úteis na condução dessa discussão. A escuta das possíveis soluções é muito importante. Incentive para que eles justifiquem suas escolhas e informem o que julgaram difícil ou fácil. Peça que as duplas compartilhem suas soluções, seja por áudio, vídeo, fotos ou por meio do Painel de Soluções interativo, no Padlet, no Jamboard ou no arquivo de acesso coletivo.
Convite às famílias
Sugira aos alunos que envolvam os familiares na discussão das estratégias para chegar às soluções é um momento favorável para interação e troca de conhecimentos. Entretanto, é importante tomar cuidado porque, apesar da indicação, as pessoas que convivem com os alunos nesse momento de reclusão, podem estar envolvidos com outros afazeres.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Érica Fernanda Barbosa dos Santos.
Mentor: Tatiane Cristina Guadagnucci.
Especialista de área: Rita Batista.
Habilidade da BNCC
NÃO HÁ.
Objetivos específicos
Estimular a compreensão de que resolver problema é um processo de investigação para transformar a linguagem usual em representação matemática, estimular o aluno a ser protagonista da sua aprendizagem e gerenciar seus erros e acertos.
Conceito-chave
Problemas de investigação, regularidades.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não.