Guia de Interação
Plano de Aula
Plano de aula: Translações no plano
Plano 2 de uma sequência de 5 planos. Veja todos os planos sobre Simetrias
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Marcia Maria Viana Suriano
Mentor: Renata S. Gonçalves
Especialista de área: Pricilla Mendes Cerqueira
Objetivos específicos
- Construir o conceito de simetria de translação;
- Estudar a movimentação de polígonos no plano cartesiano, trabalhando a sua posição original e localização da forma após transformações.
Conceito-chave
Simetria de translação
Recursos necessários
Folha de atividades impressa, cartões numerados conforme anexo da atividade, Datashow (opcional)
Leitura Complementar
Geometria das transformações. Disponível em: <https://novaescola.org.br/conteudo/2711/geometria-das-transformacoes> Acesso em: 06/02/2018
Habilidades BNCC:
Objetivos de aprendizagem
- Construir o conceito de simetria de translação;
- Estudar a movimentação de polígonos no plano cartesiano, trabalhando a sua posição original e localização da forma após transformações.
Resumo da aula
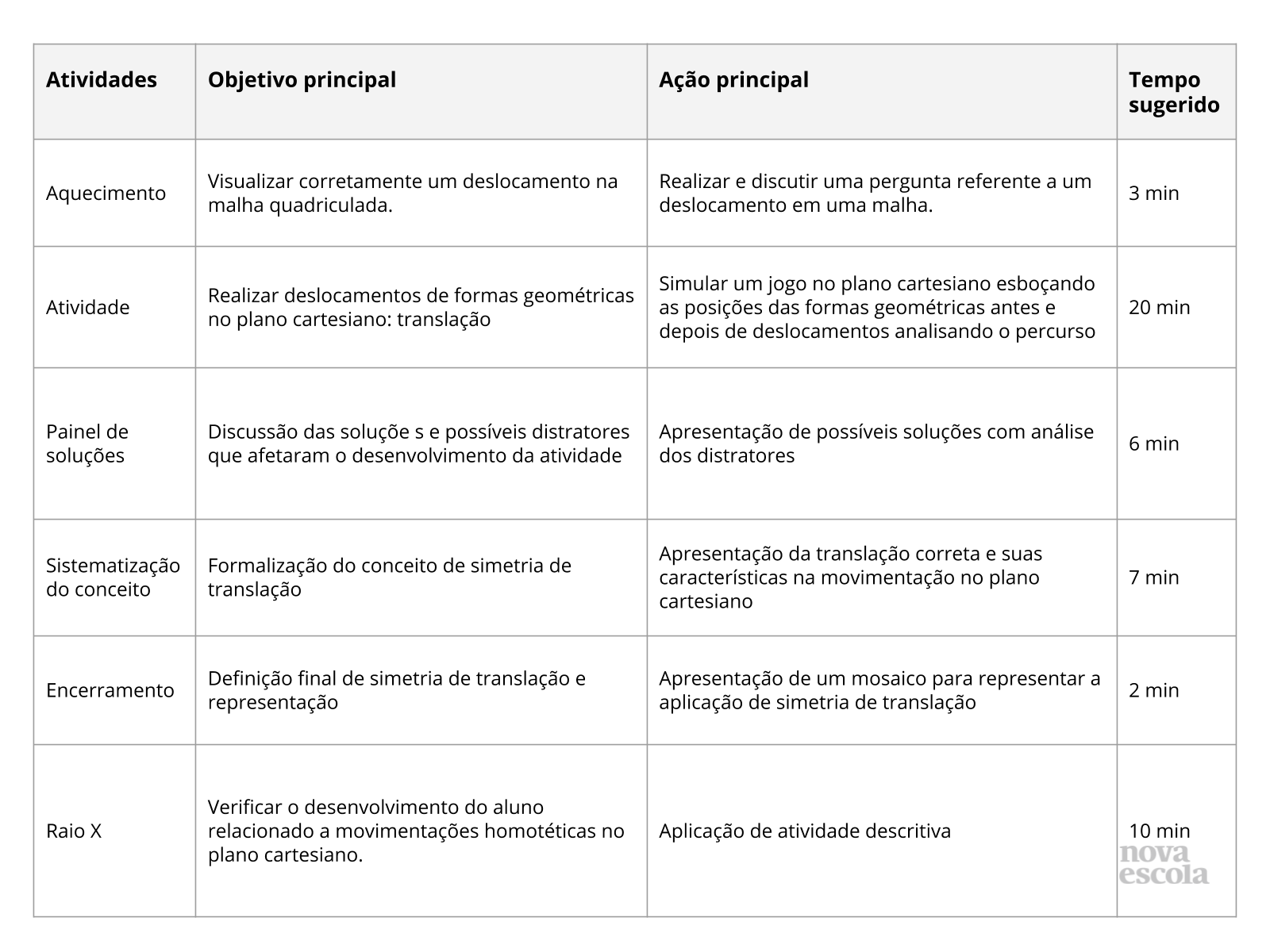 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Propósito: Enfatizar os conceitos a serem abordados levando os alunos a refletirem sobre a movimentação dos vértices de polígonos no plano cartesiano, trabalhando a sua localização antes e após as transformações isométricas nos pares ordenados que o representam: translação
Orientações: Apresente o objetivo da aula aos alunos conforme slide simplificado acima. Tenha em mente o propósito da aula determinado aqui.
Aquecimento
Tempo sugerido: 3 minutos.
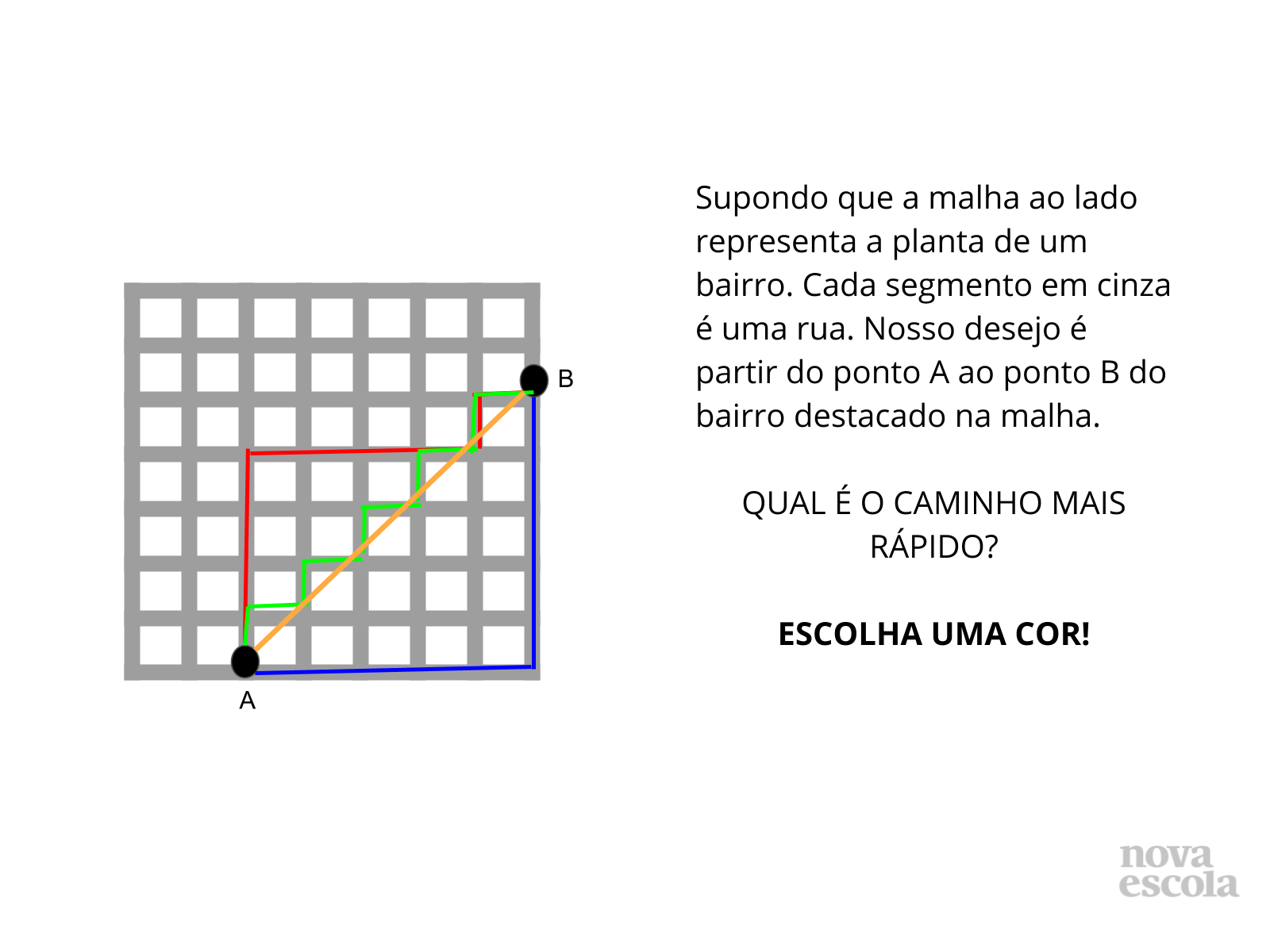
Propósito: Visualizar corretamente um deslocamento na malha quadriculada.
Orientação: Apresente a malha a turma. Faça aos alunos a pergunta do slide. Diga que deverão escolher a cor que corresponde a resposta sugerida por eles. Complemente suas respostas.
Discuta com a turma:
- Você saberia dizer qual é o caminho mais rápido considerando as informações do problema?
- Por que não é possível escolher o caminho laranja?
- Qual a diferença de distância entre os três outros caminhos?
Atividade Principal
Tempo sugerido: 20 minutos (slides 4, 5 e 6).
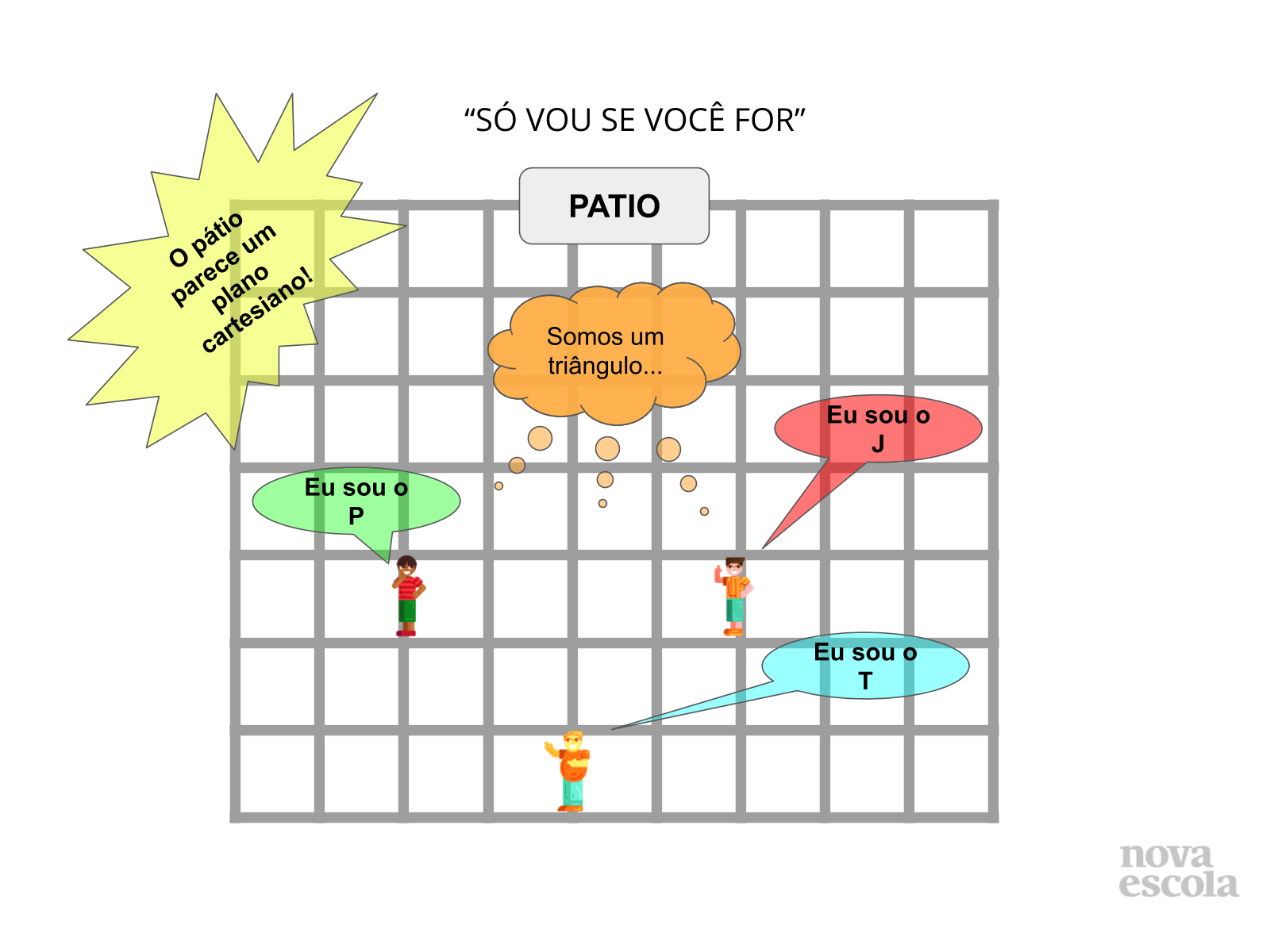
Propósito: Construir o conceito de simetria de translação
Orientação: Os alunos serão convidados a conhecer a brincadeira criada pelos amigos Pedro, Tiago e João. A sugestão é que após a apresentação os alunos representem no plano cartesiano a atividade realizada pelos três amigos. Divida a turma em trios. Peça aos alunos que dêem uma boa lida na explicação da brincadeira. Feito isso deverão seguir o roteiro de atividade disponível para a impressão e realizar as atividades solicitadas. Eles observarão o movimento do triângulo desenhado no plano.
Discuta com a turma:
- De que forma é encontrada a localização de um ponto no plano cartesiano através de um par ordenado?
- E se marcarmos um ponto no plano, como representá-lo através de um par ordenado?
- O que é necessário para movimentar a figura no plano sem que ela se deforme?
- Você conseguiria determinar a distância entre a figura original e a deslocada através de um par ordenado? Explique aos alunos o que isso significa. Peça aos alunos que façam isso por partes. Primeiro devem fazer o caminho em x, contando suas casas e depois fazer o mesmo em y.
Material Complementar:
Atividade Principal
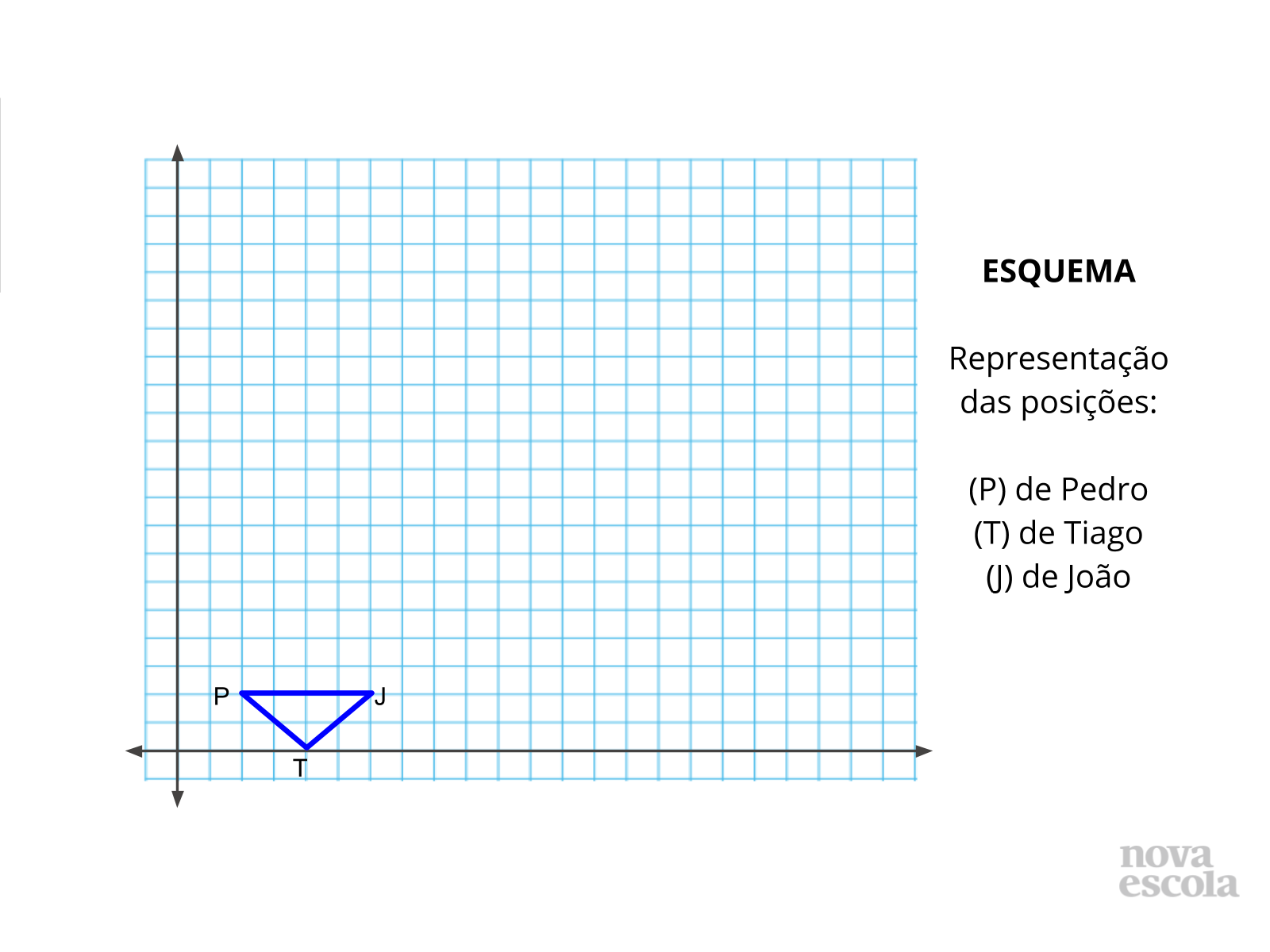
Tempo sugerido: 20 minutos (slides 4, 5 e 6).
Propósito: Construir o conceito de simetria de translação
Orientação: Os alunos serão convidados a conhecer a brincadeira criada pelos amigos Pedro , Tiago e João. A sugestão é que após a apresentação os alunos representem no plano cartesiano a atividade realizada pelos três amigos. Divida a turma em trios. Peça aos alunos que dêem uma boa lida na explicação da brincadeira. Feito isso deverão seguir o roteiro de atividade disponível para a impressão e realizar as atividades solicitadas. Saliente que eles farão uma análise do movimento do triângulo formado no plano. Incentive-os a tirarem conclusões a respeito dos movimentos. A percepção visual presente na atividade de aquecimento precisa estar, também, na mente dos alunos, principalmente na construção da tabela.
Discuta com a turma
- De que forma é encontrada a localização de um ponto no plano cartesiano através de um par ordenado?
- E se marcarmos um ponto no plano, como representá-lo através de um par ordenado?
- O que é necessário para movimentar a figura no plano sem que ela se deforme?
- Você conseguiria determinar a distância entre a figura original e a deslocada através de um par ordenado? Explique aos alunos o que isso significa. Peça aos alunos que façam isso por partes. Primeiro devem fazer o caminho em x, contando suas casas e depois fazer o mesmo em y, como no aquecimento.(Nesse caso o aluno estará determinando e representando a variação do deslocamento em x e y; não é necessário formalizar esse fato).
Material Complementar:
Atividade Principal

Tempo sugerido: 20 minutos (slides 4, 5 e 6).
Propósito: Construir o conceito de simetria de translação
Orientação: Os alunos serão convidados a conhecer a brincadeira criada pelos amigos Pedro tiago e João. A sugestão é que após a apresentação os alunos representem no plano cartesiano a atividade realizada pelos três amigos. Divida a turma em trios. Peça aos alunos que dêem uma boa lida na explicação da brincadeira. Feito isso deverão seguir o roteiro de atividade disponível para a impressão e realizar as atividades solicitadas. Saliente que eles farão uma análise do movimento do triângulo formado no plano. Incentive-os a tirarem conclusões a respeito dos movimentos. A percepção visual presente na atividade de aquecimento precisa estar, também, na mente dos alunos, principalmente na construção da tabela.
Discuta com a turma:
- De que forma é encontrada a localização de um ponto no plano cartesiano através de um par ordenado?
- E se marcarmos um ponto no plano, como representá-lo através de um par ordenado?
- O que é necessário para movimentar a figura no plano sem que ela se deforme?
- Você conseguiria determinar a distância entre a figura original e a deslocada através de um par ordenado? Explique aos alunos o que isso significa. Peça aos alunos que façam isso por partes. Primeiro devem fazer o caminho em x, contando suas casas e depois fazer o mesmo em y, como no aquecimento.(Nesse caso o aluno estará determinando e representando a variação do deslocamento em x e y; não é necessário formalizar esse fato).
Material Complementar:
Discussão da Solução
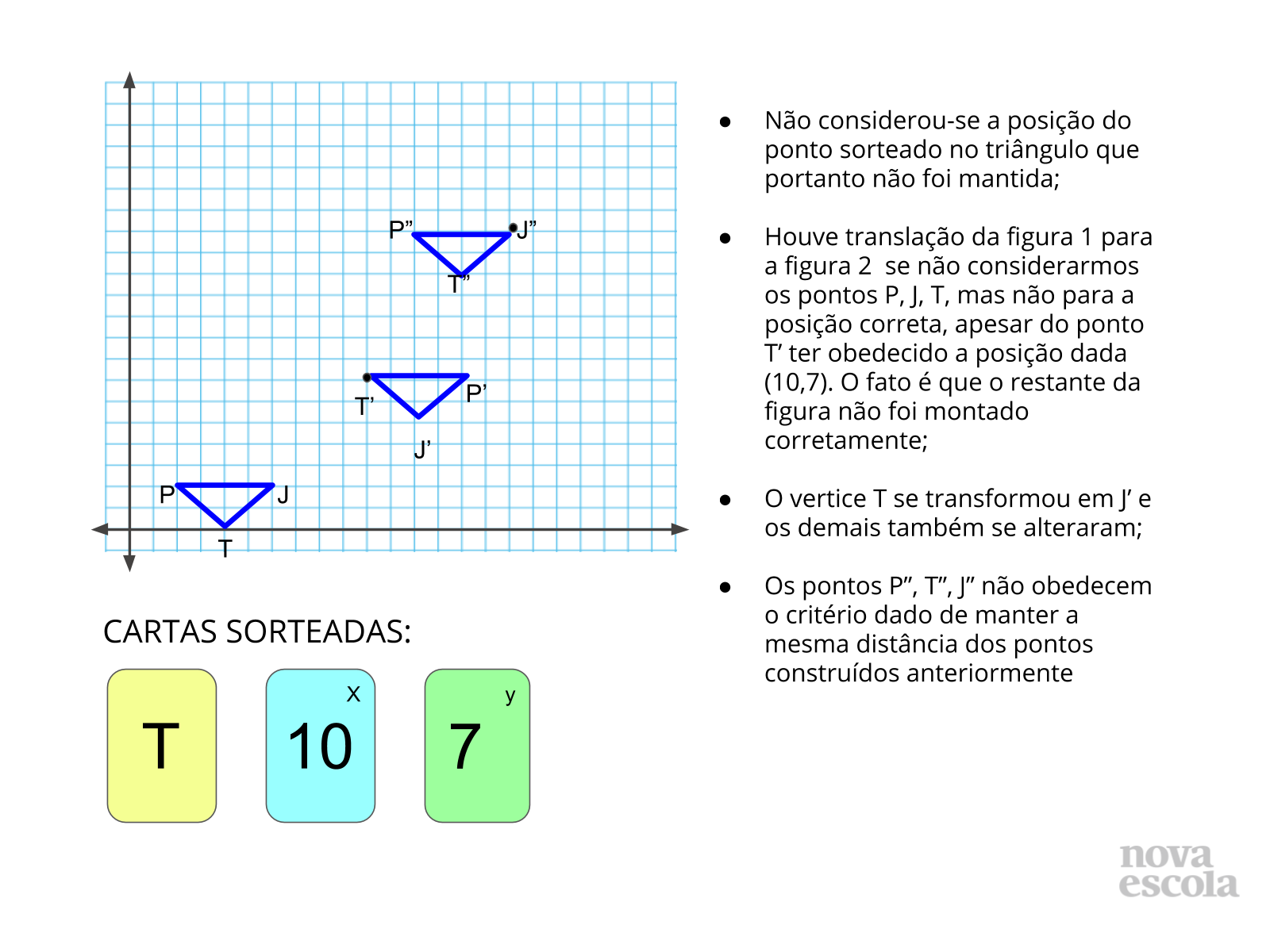
Tempo sugerido: 6 minutos (slides 7, 8 e 9).
Propósito: Discutir o conceito construído através de imagens dos possíveis resultados obtidos pelos alunos;
Orientação: Apresente a imagem do slide para discutirem alguns dos possíveis equívocos ou distorções apresentadas nas atividades desenvolvidas. Através desse momento os alunos perceberão que mínimos detalhes podem impedir que a transformação desejada aconteça de fato. Eles perceberão que é necessário manter todos os critérios da figura original, inclusive o ponto simétrico correspondente. Através do slide 9 é possível analisar distorções variadas de deslocamento no plano, divergentes do solicitado na atividade. O último slide da discussão apresenta a movimentação correta segundo a sugestão de cartas sorteadas.
Discuta com a turma:
- Como podemos definir o primeiro movimento solicitado na atividade?
- Qual a distância entre os três pontos da figura original e seus respectivos simétricos?
- Todas as figuras obedecem o mesmo critério de distanciamento? O que isso quer dizer?
Discussão da Solução
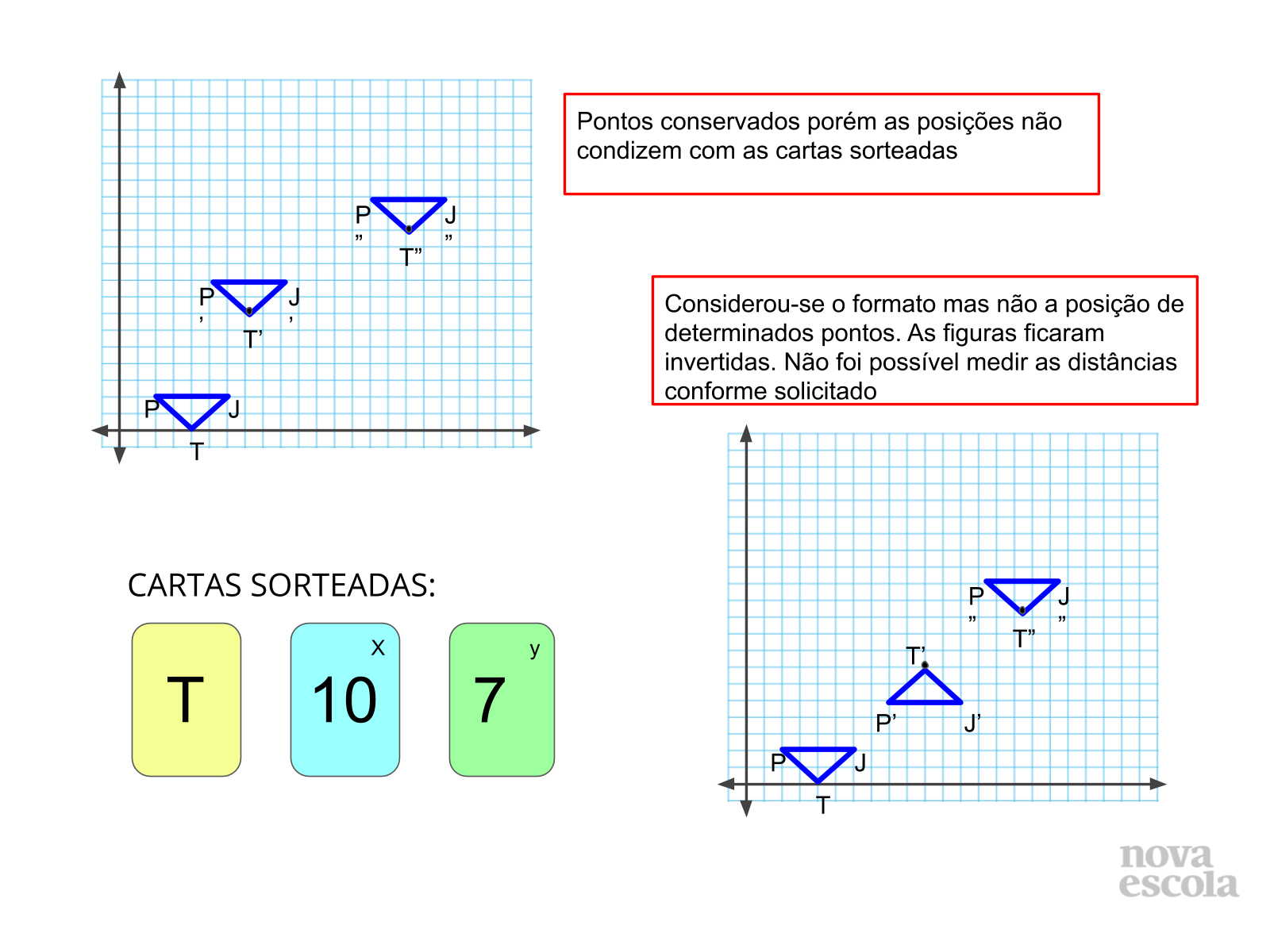
Tempo sugerido: 6 minutos (slides 7, 8 e 9).
Propósito: Discutir o conceito construído através de imagens dos possíveis resultados obtidos pelos alunos;
Orientação: Apresente a imagem do slide para discutirem alguns dos possíveis equívocos ou distorções apresentadas nas atividades desenvolvidas. Através desse momento os alunos perceberão que mínimos detalhes podem impedir que a transformação desejada aconteça de fato. Eles perceberão que é necessário manter todos os critérios da figura original, inclusive o ponto simétrico correspondente. Através do slide 9 é possível analisar distorções variadas de deslocamento no plano, divergentes do solicitado na atividade. O último slide da discussão apresenta a movimentação correta segundo a sugestão de cartas sorteadas.
Discuta com a turma:
- Como podemos definir o primeiro movimento solicitado na atividade?
- Qual a distância entre os três pontos da figura original e seus respectivos simétricos?
- Todas as figuras obedecem o mesmo critério de distanciamento? O que isso quer dizer?
Discussão da Solução
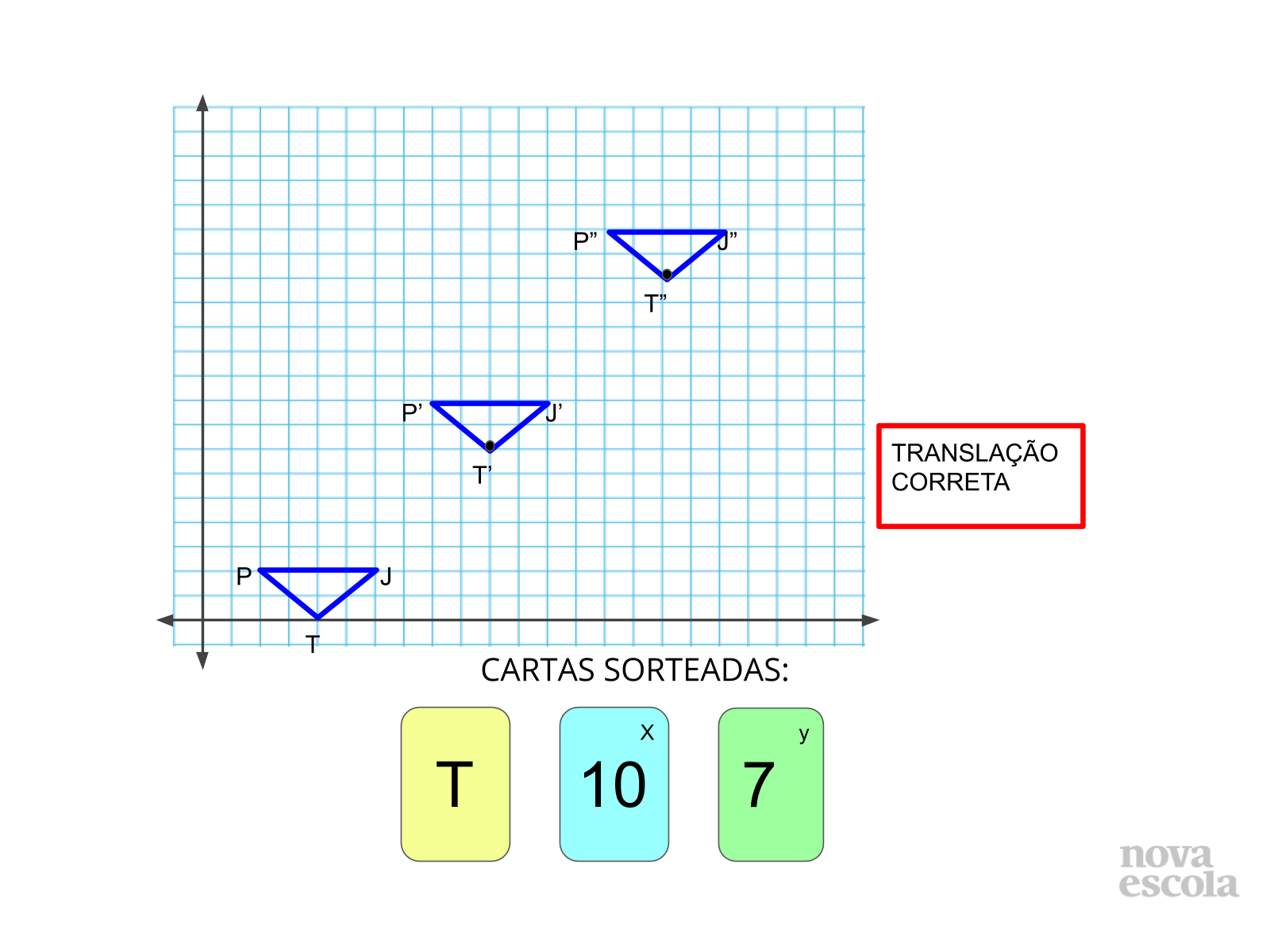
Tempo sugerido: 6 minutos (slides 7, 8 e 9).
Propósito: Discutir o conceito construído através de imagens dos possíveis resultados obtidos pelos alunos;
Orientação: Apresente a imagem do slide para discutirem alguns dos possíveis equívocos ou distorções apresentadas nas atividades desenvolvidas. Através desse momento os alunos perceberão que mínimos detalhes podem impedir que a transformação desejada aconteça de fato. Eles perceberão que é necessário manter todos os critérios da figura original, inclusive o ponto simétrico correspondente. Através do slide 9 é possível analisar distorções variadas de deslocamento no plano, divergentes do solicitado na atividade. O último slide da discussão apresenta a movimentação correta segundo a sugestão de cartas sorteadas.
Discuta com a turma:
- Como podemos definir o primeiro movimento solicitado na atividade?
- Qual a distância entre os três pontos da figura original e seus respectivos simétricos?
- Todas as figuras obedecem o mesmo critério de distanciamento? O que isso quer dizer?
Sistematização
Tempo sugerido: 7 minutos.
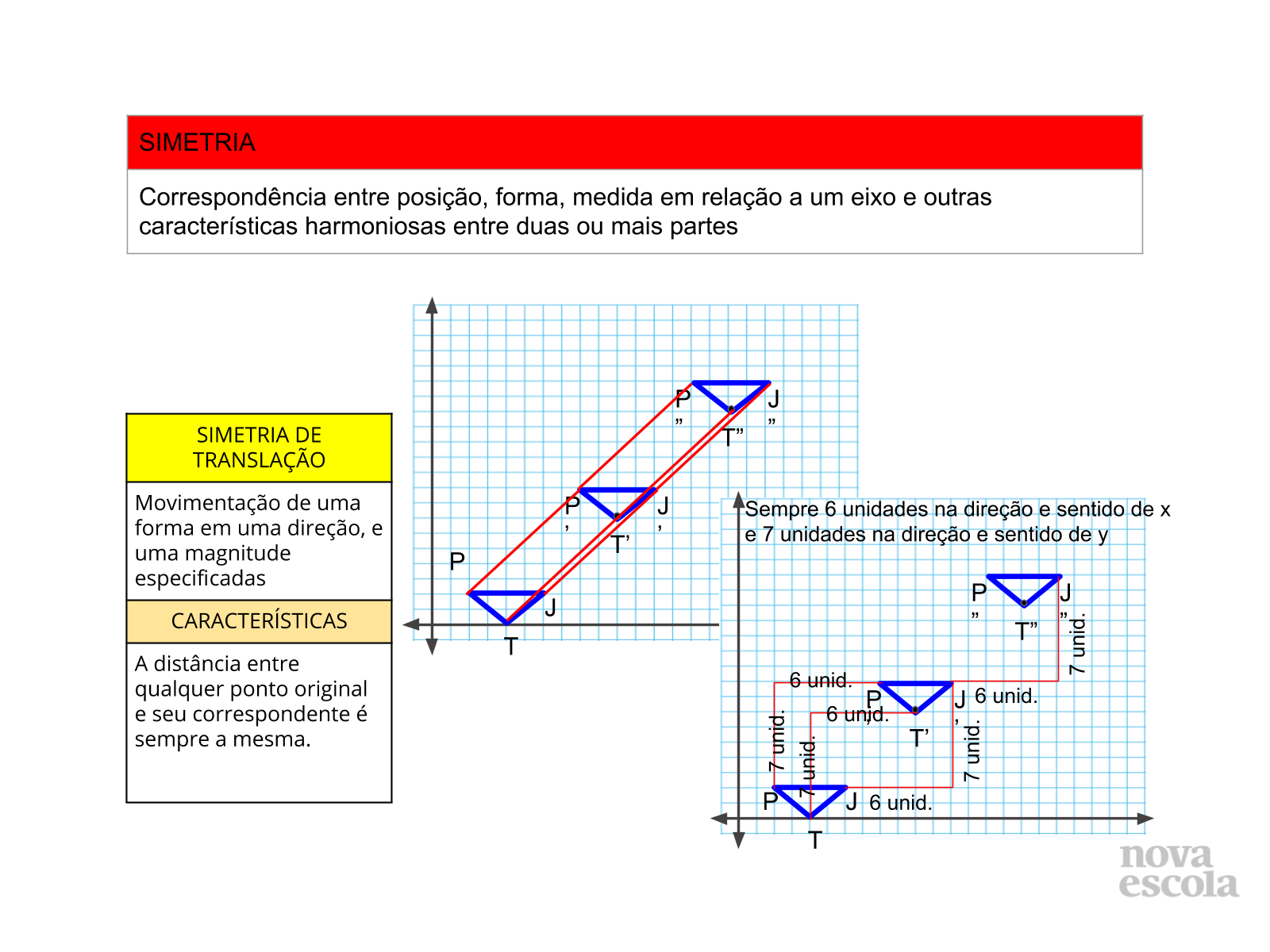
Propósito: Concluir a atividade através de definições formais definindo simetria de translação.
Orientação: Apresente as definições de simetria e posteriormente de simetria de translação para a turma para a formalização do conceito desenvolvido. Demonstre através das imagens que a atividade proposta desenvolve tal conceito de forma precisa e que atende as características de simetria de translação apresentadas.
Encerramento

Tempo sugerido: 2 minutos
Propósito: Aplicar a definição formalizada
Orientação: Peça aos alunos que observem a imagem. Eles perceberão que todo conceito construído e formalizado está presente no mosaico.
Raio X
Tempo sugerido: 10 minutos
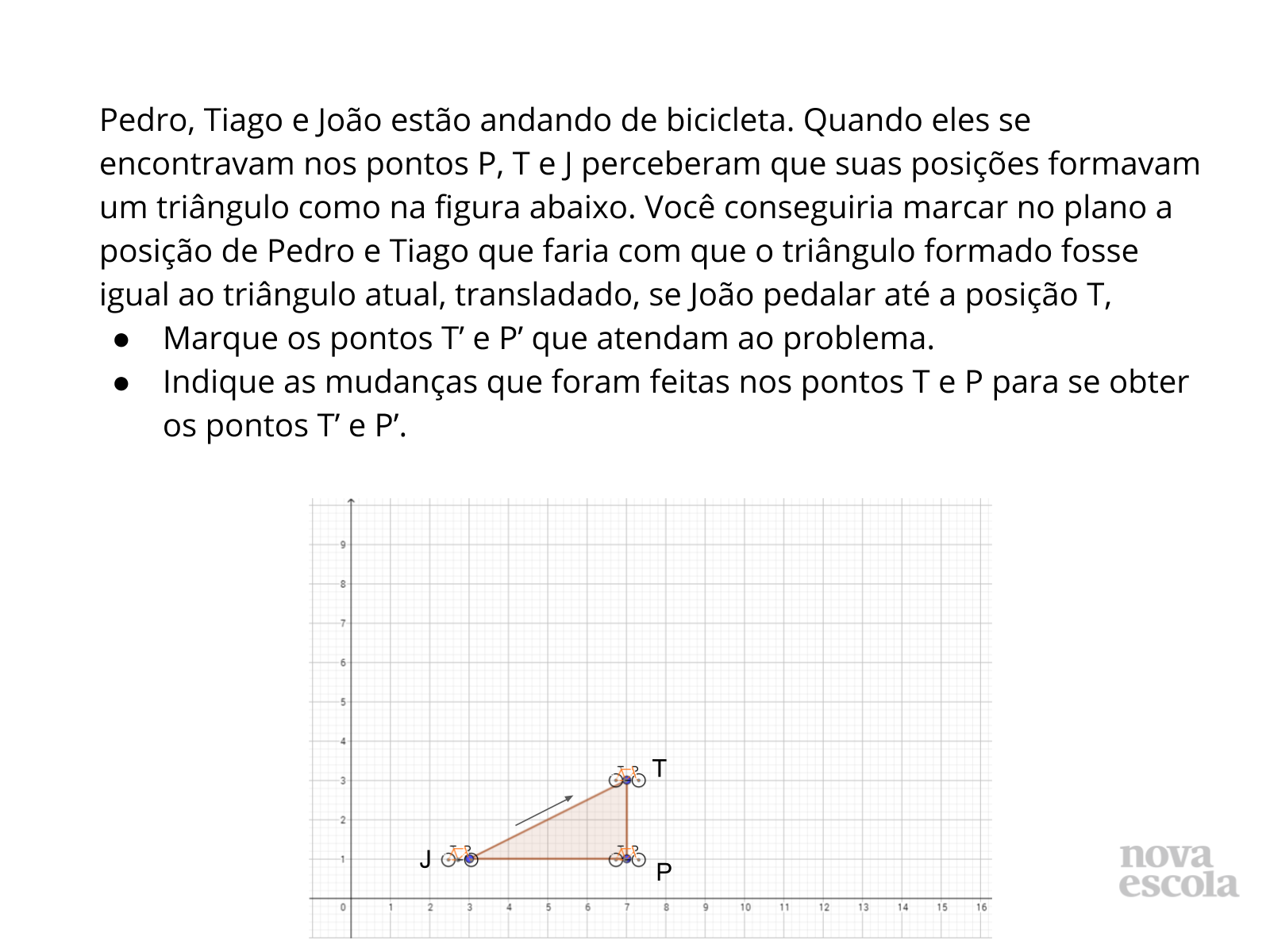
Propósito: Verificar a capacidade dos alunos em analisar transformações isométricas de forma qualitativa.
Orientação: Peça que os alunos anotem os respectivos pares ordenados correspondentes aos pontos P, T e J e aos pontos P’, T’ e J’ e compare os pontos correspondentes. Eles deverão perceber que foi realizada a mesma transformação em cada um dos pontos.
Discuta com a turma:
- Como seria o deslocamento da bicicleta J?
- Como seria o deslocamento da bicicleta T?
- Como seria o deslocamento da bicicleta P?
- O que acontece com os respectivos pares ordenados que representam os pontos P, T e J? Analise a quantidade de unidades deslocadas na vertical e na horizontal em cada um dos pontos.
Material Complementar:
Sugestão de adaptaçãopara ensino remoto
Código do plano
MAT6_18GEO02
Recursos
- Necessários: Folha sulfite, lápis, caderno
- Opcionais: Meet, Zoom, WhatsApp
Introdução à transformações: https://pt.khanacademy.org/math/basic-geo/basic-geo-transformations-congruence/transformations-intro-basic-geo/v/introduction-to-transformations
Translação de Formas: https://pt.khanacademy.org/math/basic-geo/basic-geo-transformations-congruence/basic-geometry-translations/v/drawing-image-of-translation
Vídeo: https://www.youtube.com/watch?v=HpBZUTUBU80
Para este plano, foque na etapa: Atividade Principal
Atividade Principal
Você pode propor uma aula invertida. Para isso, os alunos precisam ter acesso aos slides (4, 5 e 6). Encaminhe pelo WhatsAppp ou outro meio de comunicação combinado com eles (Meet, Hangout, Zoom). No primeiro momento eles precisam desenhar o plano cartesiano e representar a posição dos amigos no slide 1. O conceito de par ordenado precisa estar sistematizado pelos alunos. Caso contrário, sugerimos que seja feito de forma síncrona. Em seguida, oriente os alunos a imprimir ou reproduzir as cartas do arquivo enviado. Nessa hora é interessante a participação de algum familiar para que o jogo seja realizado. Você pode gravar um áudio ensinando as regras e dando dicas de como realizar esse jogo. Peça que façam os registros das cartas que foram sorteadas, tirem fotos e/ou encaminhem para você. É importante que sigam o roteiro. No dia do encontro, você pode retomar com os alunos e fazer o “Discuta com a turma” para que seja os conceitos sejam revistados e trabalhados. Dê um tempo para que eles falem sobre as dificuldades e possíveis equívocos que surgiram durante o jogo.
Encerramento
Para encerrar a aula sugira o vídeo https://www.youtube.com/watch?v=HpBZUTUBU80 que mostra a simetria de translação no plano cartesiano.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa. Portanto, indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos. Nessa aula seria importante a participação de algum familiar para que o aluno possa realizar o jogo.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Marcia Maria Viana Suriano
Mentor: Renata S. Gonçalves
Especialista de área: Pricilla Mendes Cerqueira
Objetivos específicos
- Construir o conceito de simetria de translação;
- Estudar a movimentação de polígonos no plano cartesiano, trabalhando a sua posição original e localização da forma após transformações.
Conceito-chave
Simetria de translação
Recursos necessários
Folha de atividades impressa, cartões numerados conforme anexo da atividade, Datashow (opcional)
Leitura Complementar
Geometria das transformações. Disponível em: <https://novaescola.org.br/conteudo/2711/geometria-das-transformacoes> Acesso em: 06/02/2018