Atividade Principal
Plano de Aula
Plano de aula: Aumentos e descontos sucessivos
Plano 5 de uma sequência de 5 planos. Veja todos os planos sobre Aumentos e descontos percentuais
Por: Luiz Filipe Trovão
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Luiz Filipe Trovão
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA02 - Resolver e elaborar problemas que envolvam porcentagens, como os que lidam com acréscimos e decréscimos simples, utilizando estratégias pessoais, cálculo mental e calculadora, no contexto de educação financeira, entre outros.
Objetivos específicos
- Analisar situações problema do cotidiana envolvendo acréscimos e descontos percentuais sucessivos.
Conceito-chave
Acréscimos e descontos sucessivos.
Recursos necessários
Lápis, borracha, caderno e calculadora.
Habilidades BNCC:
Objetivos de aprendizagem
- Analisar situações problema do cotidiana envolvendo acréscimos e descontos percentuais sucessivos.
Resumo da aula
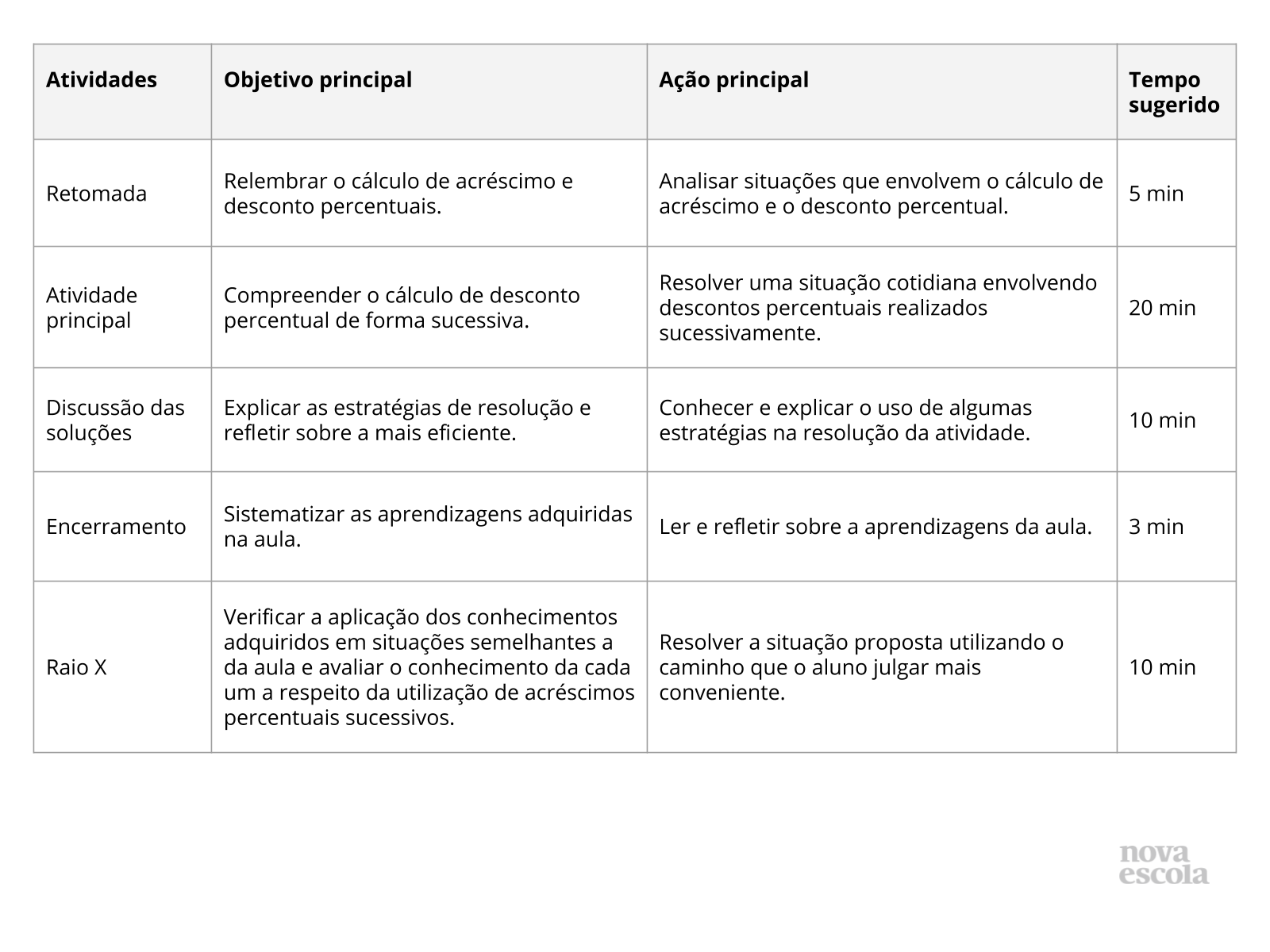 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma. Caso não seja possível a projeção, escreva o objetivo no quadro.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo sugerido: 5 minutos (slides 3 e 4)
Orientação: Professor, projete essa série de slides para a sala. Caso não seja possível a projeção, leia a pergunta presente no balão de fala e copie no quadro ou em um cartaz as situações presentes no slide 3, bem como as soluções presentes no slide 4.
Inicialmente, realize a pergunta presente no balão de fala, para os alunos: “Você se lembra como efetuar o cálculo de acréscimos ou descontos percentuais?”. A intenção dessa pergunta é apresentar o que será trabalhado nessa retomada.
Após essa breve introdução, passe para as duas situações presentes no slide 3, uma referente a desconto e a outra referente a acréscimo percentual, não aponte isso para os alunos, deixam que eles percebam, se familiarizando com os termos.
Disponibilize um breve momento para que os alunos analisem e resolvam as duas situações propostas. Passado esse tempo, vá para o slide 4 e discuta as soluções das duas situações propostas.
Conclua com os alunos que as situações que envolvem desconto, o valor percentual calculado é subtraído do valor inicial e as situações que envolvem acréscimos, o valor percentual calculado é adicionado ao valor inicial.
Propósito: Relembrar a ideia de desconto e acréscimo percentual.
Discuta com a turma:
- As duas situações apresentadas possuem o mesmo significado?
- Ambas envolvem o cálculo de porcentagem, porém a interpretação final é a mesma nas duas situações?
- O que caracteriza o desconto em uma situação? E o acréscimo?
Retomada

Tempo sugerido: 5 minutos (slides 3 e 4)
Orientação: Professor, projete essa série de slides para sala. Caso não seja possível a projeção, leia a pergunta presente no balão de fala e copie no quadro ou em um cartaz as situações presentes no slide 3, bem como as soluções presentes no slide 4.
Inicialmente, realize a pergunta presente no balão de fala, para os alunos: “Você se lembra como efetuar o cálculo de acréscimos ou descontos percentuais?”. A intenção dessa pergunta é apresentar o que será trabalhado nessa retomada.
Após essa breve introdução, passe para as duas situações presentes no slide 3, uma referente a desconto e a outra referente a acréscimo percentual, não aponte isso para os alunos, deixam que eles percebam, se familiarizando com os termos.
Disponibilize um breve momento para que os alunos analisem e resolvam as duas situações propostas. Passado esse tempo, vá para o slide 4 e discuta as soluções das duas situações propostas.
Conclua com os alunos que as situações que envolvem desconto, o valor percentual calculado é subtraído do valor inicial e as situações que envolvem acréscimos, o valor percentual calculado é adicionado ao valor inicial.
Propósito: Relembrar a ideia de desconto e acréscimo percentual.
Discuta com a turma:
- As duas situações apresentadas possuem o mesmo significado?
- Ambas envolvem o cálculo de porcentagem, porém a interpretação final é a mesma nas duas situações?
- O que caracteriza o desconto em uma situação? E o acréscimo?
Atividade principal

Tempo sugerido: 20 minutos (slides 5 e 6)
Orientação: Imprima a atividade principal, entregue para os alunos e leia juntamente com eles a situação apresentada na atividade. Caso não seja possível a projeção, escreva a situação no quadro ou confeccione um cartaz.
Explique para os alunos que a atividade será composta por duas situações, que continuarão trabalhando a ideia de descontos e aumentos, de maneira análoga a realizada no início da aula, porém agora ele será realizado de forma sucessiva, ou seja, “um desconto sobre um valor que já sofreu um desconto” e “um aumento sobre um valor que já sofreu um aumento”, por isso, atente-se ao fato de que nesse momento serão realizados dois cálculos seguidos em cada uma das situações, procure deixar claro isso para os alunos, para eles evitem alguns erros comuns nesse tipo de situação.
Peça para que os alunos utilizem a calculadora como ferramenta auxiliar nesses cálculos, caso algumas alunos prefiram realizar o cálculo manualmente, sugira para que ele utilize a calculadora como forma de verificar o resultado obtido e para que ele pegue prática em seu uso, visando situações em que os cálculos a serem realizados serão mais extensos.
Propósito: Analisar uma situação problema envolvendo descontos sucessivos.
Discuta com a turma:
- Existe a possibilidade de realizar os dois descontos sucessivos com um único cálculo?
- Há outra forma de se determinar o valor pago pela TV?
- Existe a possibilidade de realizar os dois aumentos sucessivos com um único cálculo?
- Há outra forma de se determinar o reajuste sofrido pelo salário de Mateus?
Materiais complementares para impressão:
Resolução da Atividade Principal
Leituras:
Qual a diferença entre porcentagem e percentagem?
Atividade principal

Tempo sugerido: 20 minutos (slides 5 e 6)
Orientação: Imprima a atividade principal, entregue para os alunos e leia juntamente com eles a situação apresentada na atividade. Caso não seja possível a projeção, escreva a situação no quadro ou confeccione um cartaz.
Explique para os alunos que a atividade será composta por duas situações, que continuarão trabalhando a ideia de descontos e aumentos, de maneira análoga a realizada no início da aula, porém agora ele será realizado de forma sucessiva, ou seja, “um desconto sobre um valor que já sofreu um desconto” e “um aumento sobre um valor que já sofreu um aumento”, por isso, atente-se ao fato de que nesse momento serão realizados dois cálculos seguidos em cada uma das situações, procure deixar claro isso para os alunos, para eles evitem alguns erros comuns nesse tipo de situação.
Peça para que os alunos utilizem a calculadora como ferramenta auxiliar nesses cálculos, caso algumas alunos prefiram realizar o cálculo manualmente, sugira para que ele utilize a calculadora como forma de verificar o resultado obtido e para que ele pegue prática em seu uso, visando situações em que os cálculos a serem realizados serão mais extensos.
Propósito: Analisar uma situação problema envolvendo descontos sucessivos.
Discuta com a turma:
- Existe a possibilidade de realizar os dois descontos sucessivos com um único cálculo?
- Há outra forma de se determinar o valor pago pela TV?
- Existe a possibilidade de realizar os dois aumentos sucessivos com um único cálculo?
- Há outra forma de se determinar o reajuste sofrido pelo salário de Mateus?
Discussão da solução

Tempo sugerido: 10 minutos (slides 7 a 10)
Orientação: Inicialmente, peça para que os alunos discutam as soluções da situação proposta em duplas, sempre acompanhando-os em seus raciocínios. Em seguida, peça para que alguns alunos exponham suas resoluções. A ideia não é direcionar para que determinado aluno apresente a solução, porém quanto mais caminhos diferentes forem apresentados para se chegar na mesma resposta, mais rica será a discussão.
Após os alunos compartilharem as estratégias utilizadas na resolução da atividade, passe para essa série de slides (7 a 10). Caso não seja possível a projeção, reproduza, pelo menos os cálculos realizados para se chegar aos valores solicitados no quadro ou em um cartaz, o restante da solução poderá ser lida com a sala.
A ideia principal na solução das situações na atividade é compreender que, quando se trata de um desconto, será concluída com uma redução do valor apresentado inicialmente. E quando se trata de um aumento, será concluída com um aumento de valor. Perceba que, pelo fato de o segundo desconto (ou aumento) ser sucessivo ao primeiro, há a necessidade de realizar os cálculos um de cada vez, pois, na primeira situação, o segundo desconto é aplicado ao valor da televisão subtraído o valor do 1º desconto, e na segunda situação, o segundo reajuste é aplicado ao salário inicial adicionado o valor do 1º reajuste.
Note que o resultado final da primeira situação não é mesma coisa de se calcular 15% de R$ 1.800,00, pois esse é efetuado de uma única vez.
E o resultado final da segunda situação, não é o mesmo se calcularmos 18% de R$ 2.200,00, pois esse é efetuado de uma única vez.
Perceba que há uma instrução em relação ao uso da calculadora para encontrar o valor equivalente a porcentagem desejada.
Estimule o aluno ao uso dessa ferramenta, visto que em situaçõe que apresentarem mais do que dois descontos ou acréscimos sucessivos, os cálculos realizados manualmente podem se tornar exaustivos.
Propósito: Fazer com que os alunos percebam que o uso da calculadora pode facilitar o cálculo de porcentagens e que dois descontos sucessivos (10% e 5%) não podem ser acumulados como apenas um que é a soma dos dois (15%).
Discuta com a turma:
- Há como realizar essa cálculo em uma calculadora sem a função de porcentagem (%)?
- O desconto de 10% seguido do desconto de 5%, equivale a um desconto de 15%? Por que?
- O aumento de 8% seguido de um aumento de 10%, equivale a um aumento de 18%? Por que?
- É possível encontrar o valor final, utilizando a calculadora, sem dividir a resolução em etapas?
Discussão da solução
Tempo sugerido: 10 minutos (slides 7 a 10)
Orientação: Inicialmente, peça para que os alunos discutam as soluções da situação proposta em duplas, sempre acompanhando-os em seus raciocínios. Em seguida, peça para que alguns alunos exponham suas resoluções. A ideia não é direcionar para que determinado aluno apresente a solução, porém quanto mais caminhos diferentes forem apresentados para se chegar na mesma resposta, mais rica será a discussão.
Após os alunos compartilharem as estratégias utilizadas na resolução da atividade, passe para essa série de slides (7 a 10). Caso não seja possível a projeção, reproduza, pelo menos os cálculos realizados para se chegar aos valores solicitados no quadro ou em um cartaz, o restante da solução poderá ser lida com a sala.
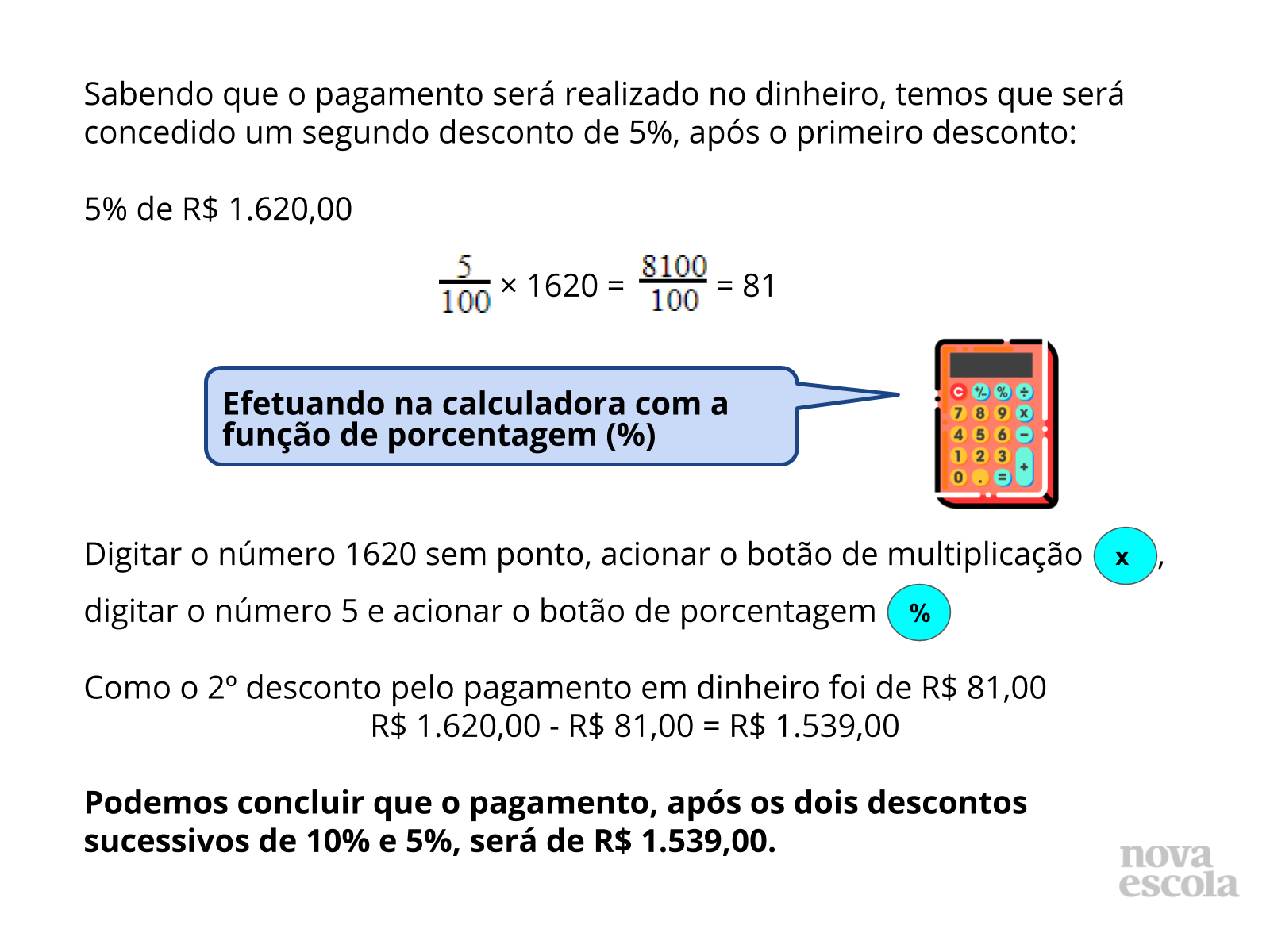
A ideia principal na solução das situações na atividade é compreender que, quando se trata de um desconto, será concluída com uma redução do valor apresentado inicialmente. E quando se trata de um aumento, será concluída com um aumento de valor. Perceba que, pelo fato de o segundo desconto (ou aumento) ser sucessivo ao primeiro, há a necessidade de realizar os cálculos um de cada vez, pois, na primeira situação, o segundo desconto é aplicado ao valor da televisão subtraído o valor do 1º desconto, e na segunda situação, o segundo reajuste é aplicado ao salário inicial adicionado o valor do 1º reajuste.
Note que o resultado final da primeira situação não é mesma coisa de se calcular 15% de R$ 1.800,00, pois esse é efetuado de uma única vez.
E o resultado final da segunda situação, não é o mesmo se calcularmos 18% de R$ 2.200,00, pois esse é efetuado de uma única vez.
Perceba que há uma instrução em relação ao uso da calculadora para encontrar o valor equivalente a porcentagem desejada.
Estimule o aluno ao uso dessa ferramenta, visto que em situaçõe que apresentarem mais do que dois descontos ou acréscimos sucessivos, os cálculos realizados manualmente podem se tornar exaustivos.
Propósito: Fazer com que os alunos percebam que o uso da calculadora pode facilitar o cálculo de porcentagens e que dois descontos sucessivos (10% e 5%) não podem ser acumulados como apenas um que é a soma dos dois (15%).
Discuta com a turma:
- Há como realizar essa cálculo em uma calculadora sem a função de porcentagem (%)?
- O desconto de 10% seguido do desconto de 5%, equivale a um desconto de 15%? Por que?
- O aumento de 8% seguido de um aumento de 10%, equivale a um aumento de 18%? Por que?
- É possível encontrar o valor final, utilizando a calculadora, sem dividir a resolução em etapas?
Discussão da solução

Tempo sugerido: 10 minutos (slides 7 a 10)
Orientação: Inicialmente, peça para que os alunos discutam as soluções da situação proposta em duplas, sempre acompanhando-os em seus raciocínios. Em seguida, peça para que alguns alunos exponham suas resoluções. A ideia não é direcionar para que determinado aluno apresente a solução, porém quanto mais caminhos diferentes forem apresentados para se chegar na mesma resposta, mais rica será a discussão.
Após os alunos compartilharem as estratégias utilizadas na resolução da atividade, passe para essa série de slides (7 a 10). Caso não seja possível a projeção, reproduza, pelo menos os cálculos realizados para se chegar aos valores solicitados no quadro ou em um cartaz, o restante da solução poderá ser lida com a sala.
A ideia principal na solução das situações na atividade é compreender que, quando se trata de um desconto, será concluída com uma redução do valor apresentado inicialmente. E quando se trata de um aumento, será concluída com um aumento de valor. Perceba que, pelo fato de o segundo desconto (ou aumento) ser sucessivo ao primeiro, há a necessidade de realizar os cálculos um de cada vez, pois, na primeira situação, o segundo desconto é aplicado ao valor da televisão subtraído o valor do 1º desconto, e na segunda situação, o segundo reajuste é aplicado ao salário inicial adicionado o valor do 1º reajuste.
Note que o resultado final da primeira situação não é mesma coisa de se calcular 15% de R$ 1.800,00, pois esse é efetuado de uma única vez.
E o resultado final da segunda situação, não é o mesmo se calcularmos 18% de R$ 2.200,00, pois esse é efetuado de uma única vez.
Perceba que há uma instrução em relação ao uso da calculadora para encontrar o valor equivalente a porcentagem desejada.
Estimule o aluno ao uso dessa ferramenta, visto que em situaçõe que apresentarem mais do que dois descontos ou acréscimos sucessivos, os cálculos realizados manualmente podem se tornar exaustivos.
Propósito: Fazer com que os alunos percebam que o uso da calculadora pode facilitar o cálculo de porcentagens e que dois descontos sucessivos (10% e 5%) não podem ser acumulados como apenas um que é a soma dos dois (15%).
Discuta com a turma:
- Há como realizar essa cálculo em uma calculadora sem a função de porcentagem (%)?
- O desconto de 10% seguido do desconto de 5%, equivale a um desconto de 15%? Por que?
- O aumento de 8% seguido de um aumento de 10%, equivale a um aumento de 18%? Por que?
- É possível encontrar o valor final, utilizando a calculadora, sem dividir a resolução em etapas?
Discussão da solução
Tempo sugerido: 10 minutos (slides 7 a 10)
Orientação: Inicialmente, peça para que os alunos discutam as soluções da situação proposta em duplas, sempre acompanhando-os em seus raciocínios. Em seguida, peça para que alguns alunos exponham suas resoluções. A ideia não é direcionar para que determinado aluno apresente a solução, porém quanto mais caminhos diferentes forem apresentados para se chegar na mesma resposta, mais rica será a discussão.
Após os alunos compartilharem as estratégias utilizadas na resolução da atividade, passe para essa série de slides (7 a 10). Caso não seja possível a projeção, reproduza, pelo menos os cálculos realizados para se chegar aos valores solicitados no quadro ou em um cartaz, o restante da solução poderá ser lida com a sala.
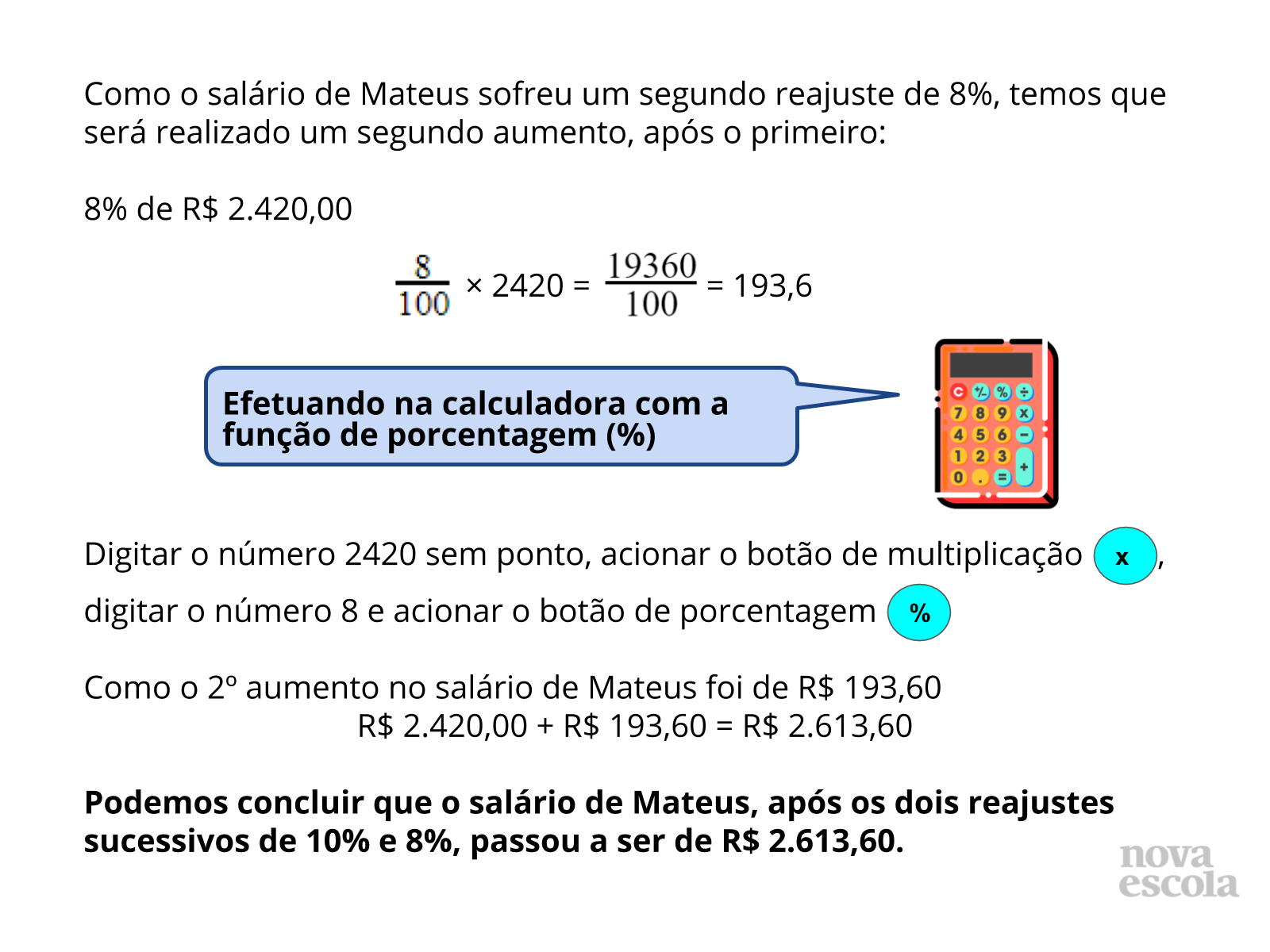
A ideia principal na solução das situações na atividade é compreender que, quando se trata de um desconto, será concluída com uma redução do valor apresentado inicialmente. E quando se trata de um aumento, será concluída com um aumento de valor. Perceba que, pelo fato de o segundo desconto (ou aumento) ser sucessivo ao primeiro, há a necessidade de realizar os cálculos um de cada vez, pois, na primeira situação, o segundo desconto é aplicado ao valor da televisão subtraído o valor do 1º desconto, e na segunda situação, o segundo reajuste é aplicado ao salário inicial adicionado o valor do 1º reajuste.
Note que o resultado final da primeira situação não é mesma coisa de se calcular 15% de R$ 1.800,00, pois esse é efetuado de uma única vez.
E o resultado final da segunda situação, não é o mesmo se calcularmos 18% de R$ 2.200,00, pois esse é efetuado de uma única vez.
Perceba que há uma instrução em relação ao uso da calculadora para encontrar o valor equivalente a porcentagem desejada.
Estimule o aluno ao uso dessa ferramenta, visto que em situaçõe que apresentarem mais do que dois descontos ou acréscimos sucessivos, os cálculos realizados manualmente podem se tornar exaustivos.
Propósito: Fazer com que os alunos percebam que o uso da calculadora pode facilitar o cálculo de porcentagens e que dois descontos sucessivos (10% e 5%) não podem ser acumulados como apenas um que é a soma dos dois (15%).
Discuta com a turma:
- Há como realizar essa cálculo em uma calculadora sem a função de porcentagem (%)?
- O desconto de 10% seguido do desconto de 5%, equivale a um desconto de 15%? Por que?
- O aumento de 8% seguido de um aumento de 10%, equivale a um aumento de 18%? Por que?
- É possível encontrar o valor final, utilizando a calculadora, sem dividir a resolução em etapas?
Encerramento

Tempo sugerido: 3 minutos
Orientação: Projete o slide e leia com os alunos a conclusão da aula. Caso não seja possível a projeção, copie no quadro ou em um cartaz as fórmulas em destaque no slide e o último cálculo ao final da conclusão.
Nesse momento de encerramento da aula, é realizada uma reflexão sobre a maneira de se calcular descontos e/ou acréscimos sucessivos. Aponte para os alunos sobre a importância de manter a ordem na realização desses cálculos, pois o único desconto ou acréscimo que é realizado tendo como referência o valor inicial é o primeiro, após ele todos os outros possuem novos valores de referência.
Conclua falando sobre a utilidade da calculadora, quando é necessária a realização de vários descontos e/ou acréscimos sucessivos. Finalize apontando o cálculo a ser feito quando a calculadora não possui a opção de porcentagem, que é a utilização da porcentagem em sua forma decimal.
Propósito: Realizar a conclusão da aula, refletindo sobre o cálculo da variação numérica e a variação percentual.
Discuta com a turma:
- É possível calcular um aumento seguido de um desconto percentual? E um desconto seguido de um aumento? Como?
- Há alguma outra forma de realizar esse cálculo de desconto utilizando a calculadora?
Raio x

Tempo sugerido: 10 minutos
Orientação: Apresente a nova situação e peça para que os alunos analisem e resolvam, em um primeiro momento individualmente e em seguida compartilhando a forma de pensar com o colega ao lado. Você pode projetar, passar no quadro ou fazer o download desta atividade e entregar para os seus alunos. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure anotar e identificar todos os comentários que surgirem. Permita o uso da calculadora nesta atividade, orientando o aluno sempre que necessário em relação a alguma dúvida que possa surgir.
Propósito: Realizar uma atividade prática relativa aos conteúdos ensinados na aula.
Discuta com a turma:
- Se somarmos as porcentagens, 6,9% + 12,9% + 4,5%, e fizermos um único aumento de 24,3%, qual seria o valor do botijão do gás?
- Por que esse valor é diferente do cálculo feito com aumentos sucessivos?
Materiais complementares para impressão:
Para os Alunos
Para o professor
Sugestão de adaptação para ensino remoto
Recursos
Necessários:
- Lápis;
- Borracha;
- Caderno;
- Whatsapp;
- Zoom.
Opcionais:
- Jambord;
- Meet.
Para este plano, foque na etapa Atividade Principal.
Aquecimento
A atividade é uma retomada de conceitos que são fundamentais para a aula. Você pode propor os questionamentos apresentados no slide usando um editor de texto (Google Docs, por exemplo) em que, de maneira colaborativa e síncrona, os alunos possam respondê-los. Também pode usar a função de áudio do Whatsapp para que um a um postem as respostas ou hipóteses sobre o assunto disparador. Oriente-os explicando que esse é um momento de retomada de conteúdos e que, caso tenham dúvidas, elas serão trabalhadas no decorrer da aula.
Atividade principal
Para a realização da atividade principal os alunos precisam ter acesso ao problema proposto. Para isso, tire uma foto e disponibilize a imagem no grupo de Whatsapp, para que eles possam pensar. Peça para tentarem resolver a atividade em três momentos. Oriente-os a filmarem ou fotografarem as estratégias e respostas, para compartilharem com você e a turma no momento da discussão das soluções.
Discussão das soluções
Organize este momento da aula usando o aplicativo Zoom e divida os alunos em duplas em salas simultâneas. Peça para discutirem entre si as soluções da situação proposta e elaborarem uma resposta conjunta para ser compartilhada com toda turma. Em seguida, volte para a sala principal e peça para que exponham as resoluções.
A ideia não é direcionar para que determinado aluno apresente a solução, porém, quanto mais caminhos diferentes forem apresentados para chegar na mesma resposta, mais rica será a discussão. Enquanto os alunos expõem as ideias, use o recurso de anotações em grupo para sistematizar as discussões.
Raio X
O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto. Envie a atividade via e-mail ou Whatsapp para os alunos e oriente-os que, quando terminarem, compartilhem novamente com você. Analise as atividades e faça devolutivas individuais expondo os pontos fortes e de atenção.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para os alunos. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa. Portanto indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Luiz Filipe Trovão
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA02 - Resolver e elaborar problemas que envolvam porcentagens, como os que lidam com acréscimos e decréscimos simples, utilizando estratégias pessoais, cálculo mental e calculadora, no contexto de educação financeira, entre outros.
Objetivos específicos
- Analisar situações problema do cotidiana envolvendo acréscimos e descontos percentuais sucessivos.
Conceito-chave
Acréscimos e descontos sucessivos.
Recursos necessários
Lápis, borracha, caderno e calculadora.










