Retomada
Plano de Aula
Plano de aula: A terça parte e o todo
Plano 5 de uma sequência de 5 planos. Veja todos os planos sobre Noções fundamentais sobre frações
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA.
Autor: Fátima Aparecida Marques Montesano
Mentor: Eliane Zanin
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
(EF03MA09) Associar o quociente de uma divisão com resto zero de um número natural por 2, 3, 4, 5 e 10 às ideias de metade, terça, quarta, quinta e décima partes.
Objetivos específicos
Aprimorar seus conhecimentos associados à ideia de terça parte com o todo.
Conceito-chave
Terça parte de um todo.
Conhecimentos prévios
Noção de dividir objetos e conjuntos de coisas em partes iguais;
em três partes; e os fatos básicos da adição.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não;
- Quadro ou flip chart para socialização dos registros;
- Projetor (opcional).
Habilidades BNCC:
Objetivos de aprendizagem
Aprimorar seus conhecimentos associados à ideia de terça parte com o todo.
Resumo da aula
Objetivo

Tempo sugerido: 2 minutos.
Propósito: Compartilhar o objetivo da aula com a turma.
Orientação: Projete ou leia o objetivo da aula para os alunos.
Retomada

Tempo sugerido: 5 minutos (slides 3 até 5).
Propósito: Retomar o conceito já estudado e preparar os alunos para a atividade da aula.
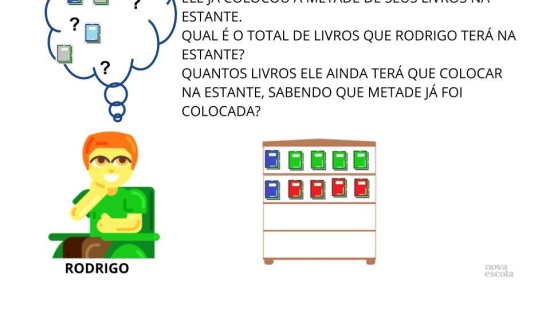
Orientação: Projete a imagem usando um projetor em sua sala, desenhe o aquário no quadro com 9 peixinhos, ou imprima a atividade e entregue para seus alunos. Leia a situação-problema com os alunos. Diga que nem todas as informações necessárias para resolver a atividade estão no enunciado. Faça as perguntas apresentadas no “Discuta com a turma” logo abaixo. Deixe que resolvam individualmente. Depois, peça para que expliquem como pensaram para resolver. Apresente os slides com as soluções somente depois dos alunos apresentarem suas estratégias e se considerar necessário.
Discuta com a turma:
- Quem tem aquário em casa? Quantos peixinhos tem?
- E neste aquário, quantos peixes tem?
- Como podemos saber quantos peixinhos devo colocar em cada aquário menor?
- Quem pode me explicar o que é um terço? Como eu consigo obter um terço?
- Vocês sabem quantos terços colocarei no aquário retangular?
Aproveite bem este momento coletivo, para contextualizar o conceito de um terço, reitere quando dividimos um todo em três partes iguais, cada parte é denominada por um terço. Mas só defina o conceito caso ninguém chegue a conclusão. É importante deixar que os alunos em primeiro momento, expressem os seus saberes sobre o conceito de um terço.
Material Complementar:
Retomada
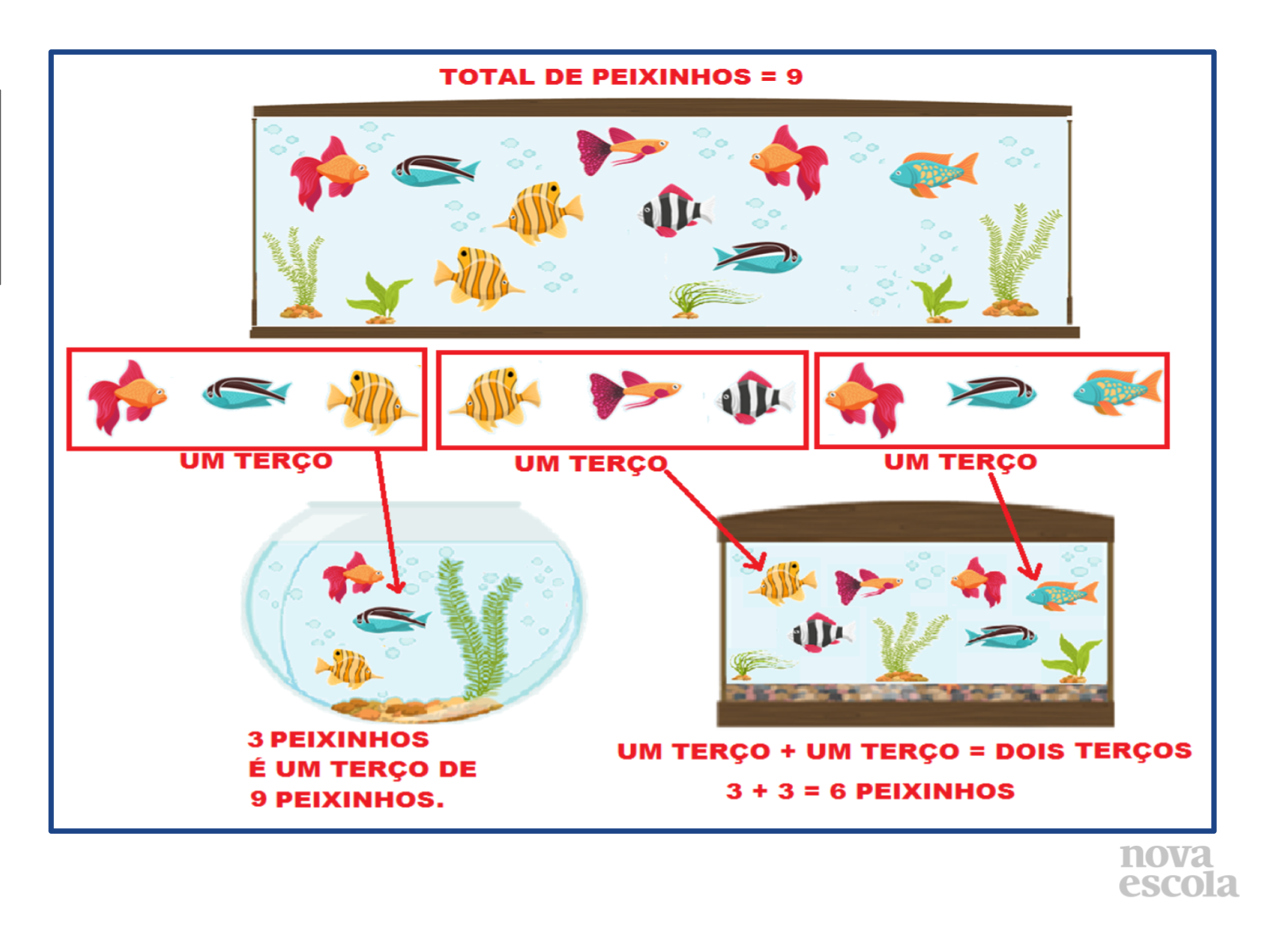
Tempo sugerido: 5 minutos (slides 3 até 5).
Propósito: Retomar o conceito já estudado e preparar os alunos para a atividade da aula.
Orientação: Projete a imagem usando um projetor em sua sala, desenhe o aquário no quadro com 9 peixinhos, ou imprima a atividade e entregue para seus alunos. Leia a situação-problema com os alunos. Diga que nem todas as informações necessárias para resolver a atividade estão no enunciado. Faça as perguntas apresentadas no “Discuta com a turma” logo abaixo. Deixe que resolvam individualmente. Depois, peça para que expliquem como pensaram para resolver. Apresente os slides com as soluções somente depois dos alunos apresentarem suas estratégias e se considerar necessário.
Discuta com a turma:
- Quem tem aquário em casa? Quantos peixinhos tem?
- E neste aquário, quantos peixes tem?
- Como podemos saber quantos peixinhos devo colocar em cada aquário menor?
- Quem pode me explicar o que é um terço? Como eu consigo obter um terço?
- Vocês sabem quantos terços colocarei no aquário retangular?
Aproveite bem este momento coletivo, para contextualizar o conceito de um terço, reitere quando dividimos um todo em três partes iguais, cada parte é denominada por um terço. Mas só defina o conceito caso ninguém chegue a conclusão. É importante deixar que os alunos em primeiro momento, expressem os seus saberes sobre o conceito de um terço.
Material Complementar:
Retomada
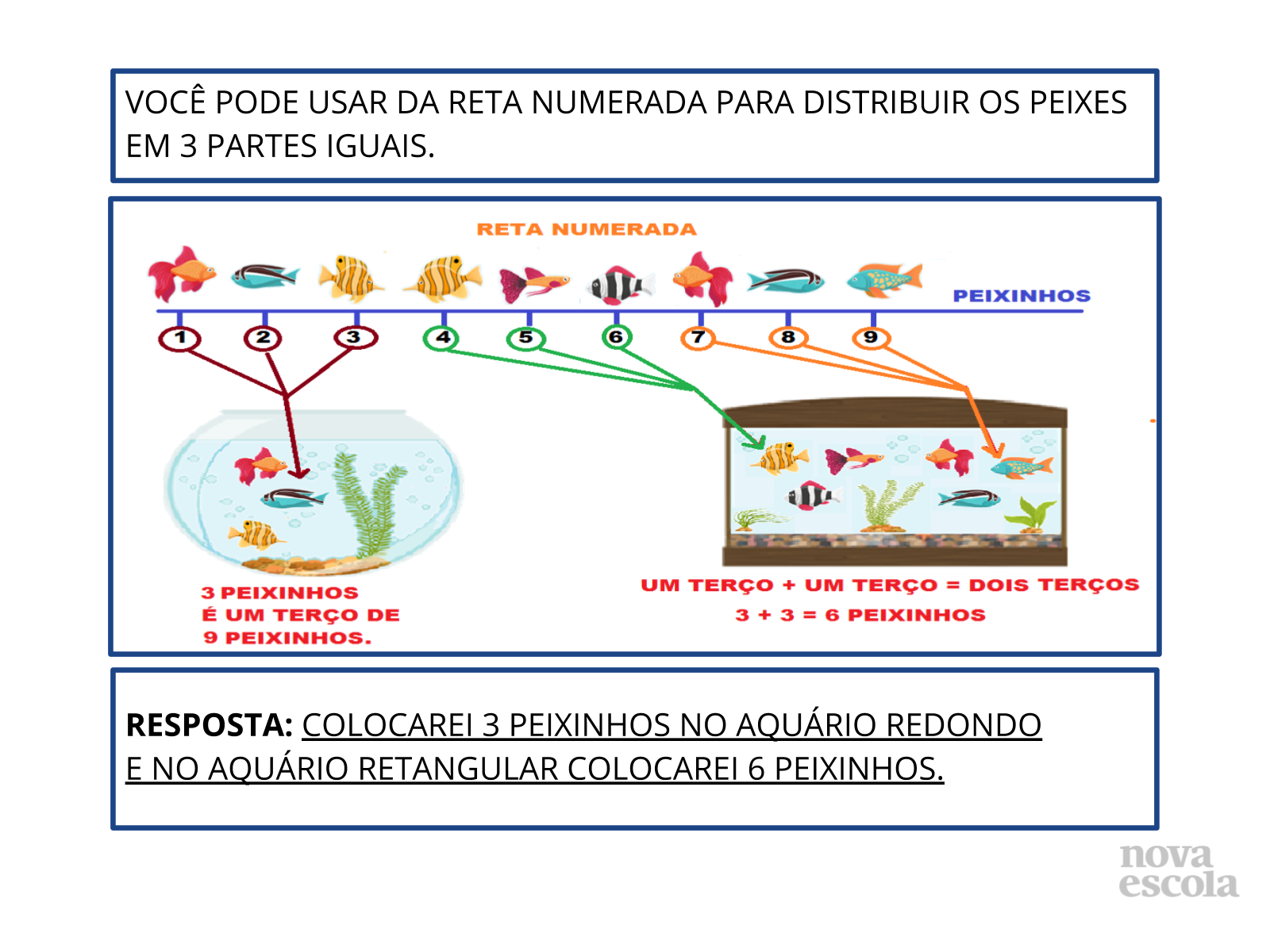
Tempo sugerido: 5 minutos (slides 3 até 5).
Propósito: Retomar o conceito já estudado e preparar os alunos para a atividade da aula.
Orientação: Projete a imagem usando um projetor em sua sala, desenhe o aquário no quadro com 9 peixinhos, ou imprima a atividade e entregue para seus alunos. Leia a situação-problema com os alunos. Diga que nem todas as informações necessárias para resolver a atividade estão no enunciado. Faça as perguntas apresentadas no “Discuta com a turma” logo abaixo. Deixe que resolvam individualmente. Depois, peça para que expliquem como pensaram para resolver. Apresente os slides com as soluções somente depois dos alunos apresentarem suas estratégias e se considerar necessário.
Discuta com a turma:
- Quem tem aquário em casa? Quantos peixinhos tem?
- E neste aquário, quantos peixes tem?
- Como podemos saber quantos peixinhos devo colocar em cada aquário menor?
- Quem pode me explicar o que é um terço? Como eu consigo obter um terço?
- Vocês sabem quantos terços colocarei no aquário retangular?
Aproveite bem este momento coletivo, para contextualizar o conceito de um terço, reitere quando dividimos um todo em três partes iguais, cada parte é denominada por um terço. Mas só defina o conceito caso ninguém chegue a conclusão. É importante deixar que os alunos em primeiro momento, expressem os seus saberes sobre o conceito de um terço.
Material Complementar:
Atividade Principal

Tempo sugerido: 20 minutos.
Propósito: Associar à ideia de terça parte com o todo.
Orientação: Entregue a atividade impressa para os alunos, ou projete a imagem. Oriente-os a lerem o enunciado e pensarem qual a melhor forma de encontrarem as respostas da situação-problema e do desafio proposto. Proporcione um momento individual para que cada aluno pense em suas próprias estratégias e depois os coloque em duplas para que discutam suas propostas de solução à situação-problema. Desafie os alunos a pensarem em outras formas de resolverem a situação além da que encontraram. Motive-os a usarem cálculo mental e exercitarem seus conhecimentos sobre os fatos básicos, soma de parcelas iguais ou na decomposição dos números. Disponibilize aos alunos materiais manipulativos (caixas de fósforos vazias, palitos, tampinhas plásticas, etc.) para que a partir da representação dos dados do problema, possam pensar sobre ele e visualizem suas hipóteses de resolução, unindo as ideias abstratas a suas representações com materiais manipulativos. Circule pela sala e faça perguntas. Questione se as duplas encontraram algum tipo de dificuldade na realização da atividade. Permita que eles reflitam sobre o quanto é bom ter conversar com o amigo sobre como resolver a atividade em parceria.
Discuta com a turma:
- Quantos centímetros tem o papel?
- Quantos cadernos dá para encapar com uma folha de 90 centímetros?
- Será que fazer um desenho ajuda a resolver?
- E usar a reta numerada, será que ajuda?
- Como seu colega pensou para resolver?
- Para encapar os 4 cadernos usaremos uma folha inteira ou precisamos de mais papel? Como podemos resolver isso?
- Estar em dupla facilitou para encontrar a resposta correta?
Materiais Complementares:
Resolução da Atividade Principal
Sugestão de leitura de estudo, Materiais Complementares:
- Frações: da aversão à compreensão. Esta produção Didática da Rede Estadual do Paraná tem por finalidade levar o aluno a aprender significativamente o conceito de frações, atribuindo sentido e significado a essa ideia matemática, para ter acesso ao conteúdo deste material clique AQUI.
- Para aprofundar o saber mais sobre os desafios para a construção do conhecimento de frações, clique AQUI.
- Vídeo sobre aula de frações, em que a turma de 3ª série tem de decidir como dividir o resto de um cálculo, clique AQUI.
- A utilização de jogos matemáticos para o ensino de frações, clique AQUI.
Painel De Soluções
Tempo sugerido: 10 minutos (slides de 7 a 9).
Propósito: Socializar os diferentes registros de resoluções dos alunos.
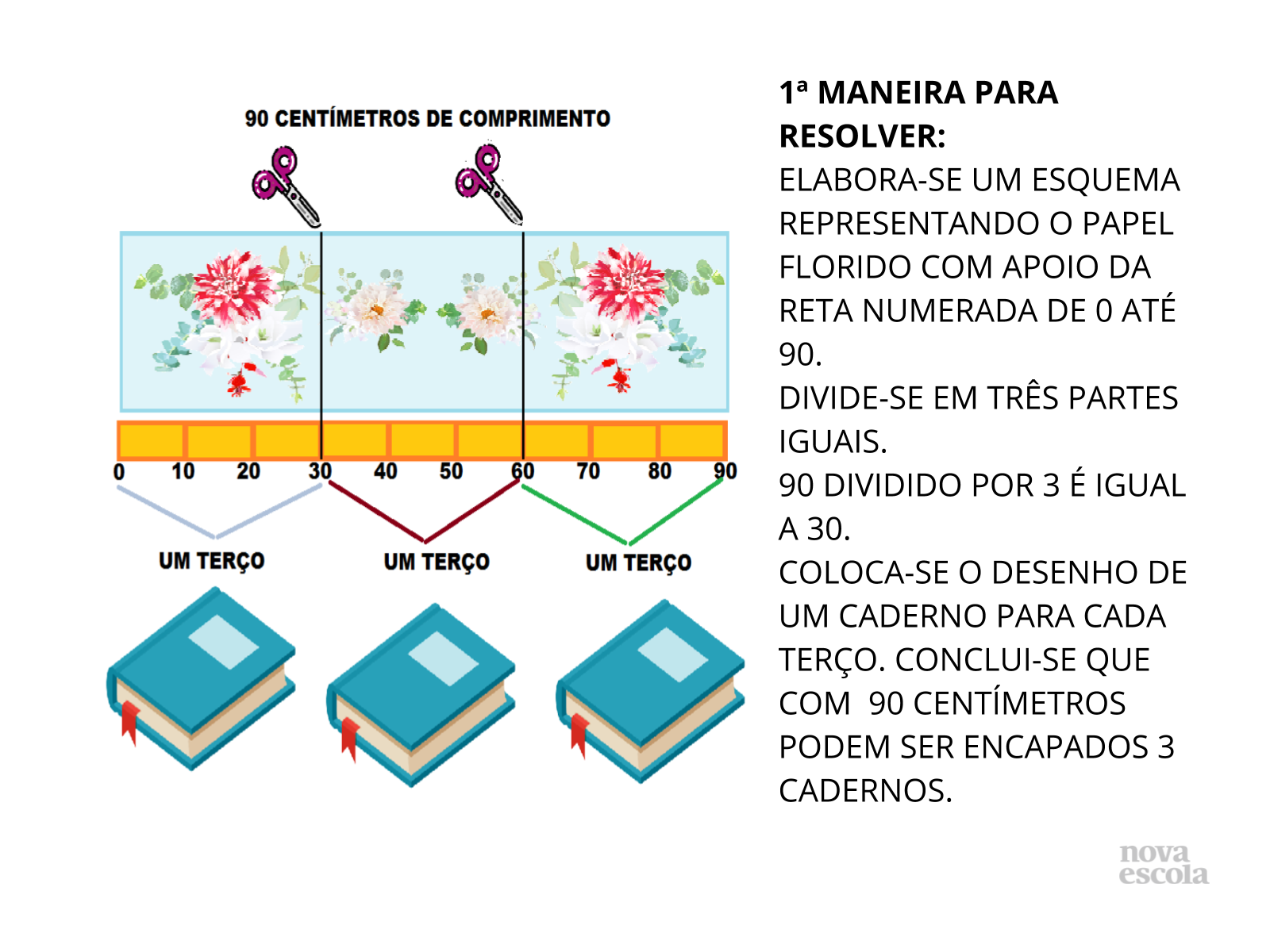
Orientação: Oriente os alunos a lerem, interpretarem o problema, a pensarem, elaborem hipóteses e apresentarem sugestões de soluções de como podem encontrar quantos centímetros precisam para encapar um caderno. Proporcione um momento individual para que cada aluno reflita alguns minutos sobre suas próprias estratégias. Depois, organize pequenos grupos (duplas ou trios) para discutirem suas ideias e juntos encontrarem a melhor solução para a situação-problema. Solicite que os alunos socializem seus registros de resolução e justifiquem seus procedimentos. Esses slides trazem possíveis soluções, porém explore as que forem apresentadas pelos alunos. Selecione alguns para registrarem suas estratégias no quadro, no flip chart ou numa folha de papel Kraft. Organize um painel de solução das duplas. Este procedimento de socializar os diferentes caminhos percorridos pelas duplas permite que cada aluno se aproprie de novas estratégias de solução para uma mesma situação-problema. Escolha um registro que não tenha sido concluído ou que não esteja totalmente correto pois, a partir da discussão da turma, os alunos terão que pensar mais para encontrarem os possíveis erros cometidos e encontrarem um jeito para alcançar a solução. Este painel de solução pode ser afixado na sala de aula servindo de apoio para novas discussões de outras situações-problema.
Observação: Não antecipe o momento dos alunos compartilharem suas descobertas, garanta que todos tenham o prazer de descobrir suas próprias soluções. Também não esqueça de valorizar a comunicação oral das crianças para que conheçam outras ideias e coloquem em jogo todo o conhecimento que já adquiriram.
Material Complementar:
Painel De Soluções
Tempo sugerido: 10 minutos (slides de 7 a 9).
Propósito: Socializar os diferentes registros de resoluções dos alunos.
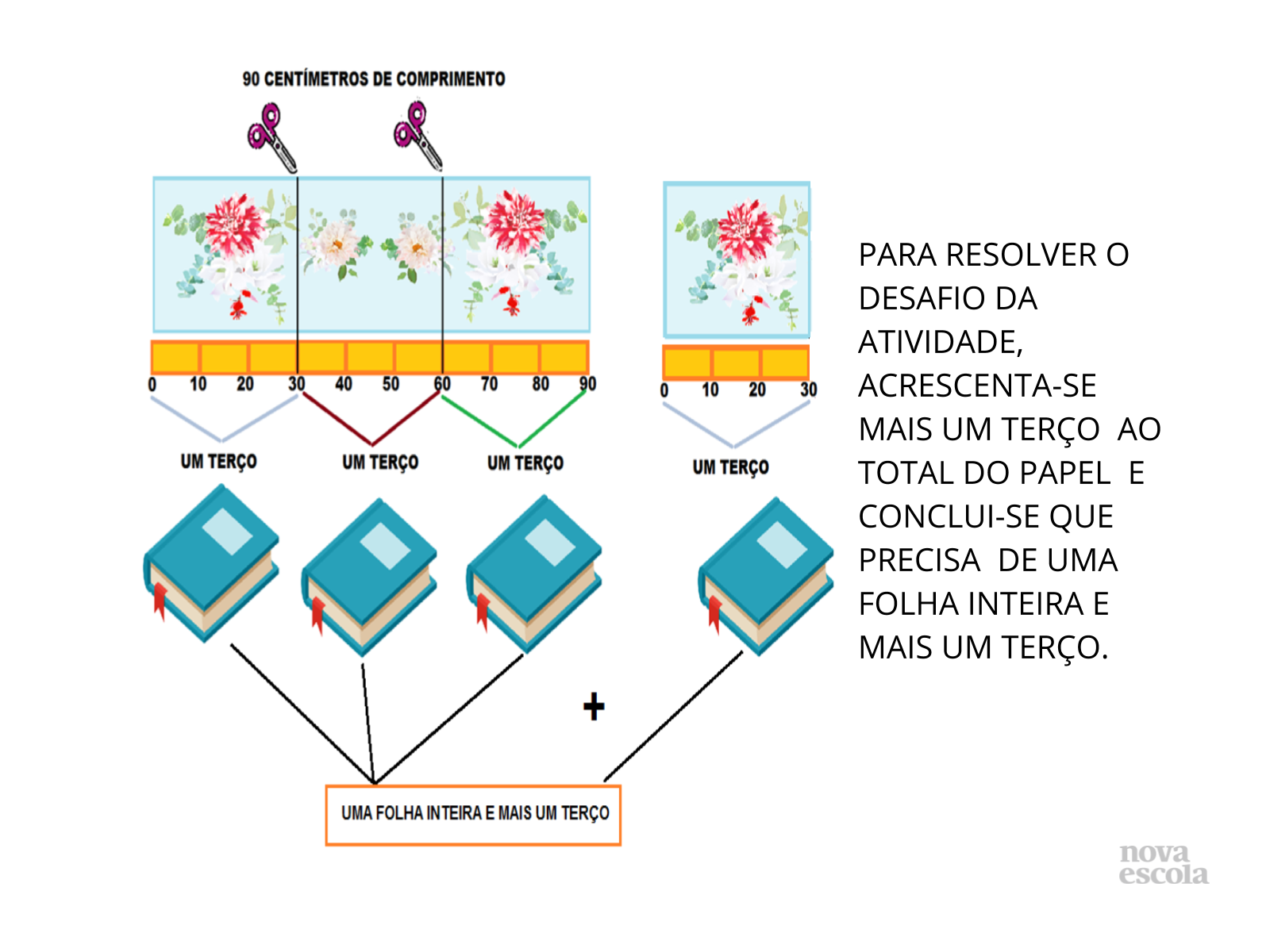
Orientação: Oriente os alunos a lerem, interpretarem o problema, a pensarem, elaborem hipóteses e apresentarem sugestões de soluções de como podem encontrar quantos centímetros precisam para encapar um caderno. Proporcione um momento individual para que cada aluno reflita alguns minutos sobre suas próprias estratégias. Depois, organize pequenos grupos (duplas ou trios) para discutirem suas ideias e juntos encontrarem a melhor solução para a situação-problema. Solicite que os alunos socializem seus registros de resolução e justifiquem seus procedimentos. Esses slides trazem possíveis soluções, porém explore as que forem apresentadas pelos alunos. Selecione alguns para registrarem suas estratégias no quadro, no flip chart ou numa folha de papel Kraft. Organize um painel de solução das duplas. Este procedimento de socializar os diferentes caminhos percorridos pelas duplas permite que cada aluno se aproprie de novas estratégias de solução para uma mesma situação-problema. Escolha um registro que não tenha sido concluído ou que não esteja totalmente correto pois, a partir da discussão da turma, os alunos terão que pensar mais para encontrarem os possíveis erros cometidos e encontrarem um jeito para alcançar a solução. Este painel de solução pode ser afixado na sala de aula servindo de apoio para novas discussões de outras situações-problema.
Observação: Não antecipe o momento dos alunos compartilharem suas descobertas, garanta que todos tenham o prazer de descobrir suas próprias soluções. Também não esqueça de valorizar a comunicação oral das crianças para que conheçam outras ideias e coloquem em jogo todo o conhecimento que já adquiriram.
Painel De Soluções
Tempo sugerido: 10 minutos (slides de 7 a 9).
Propósito: Socializar os diferentes registros de resoluções dos alunos.
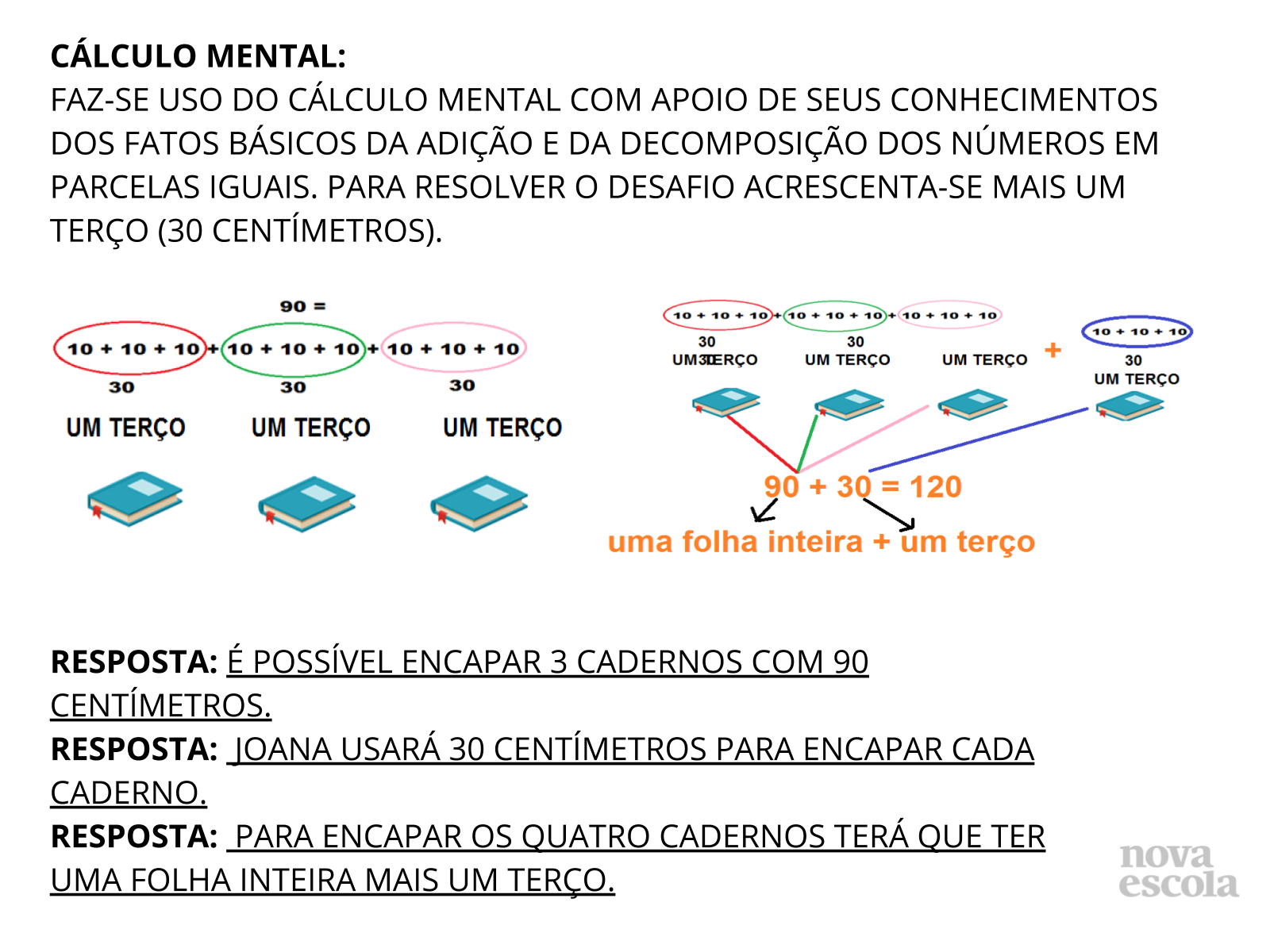
Orientação: Oriente os alunos a lerem, interpretarem o problema, a pensarem, elaborem hipóteses e apresentarem sugestões de soluções de como podem encontrar quantos centímetros precisam para encapar um caderno. Proporcione um momento individual para que cada aluno reflita alguns minutos sobre suas próprias estratégias. Depois, organize pequenos grupos (duplas ou trios) para discutirem suas ideias e juntos encontrarem a melhor solução para a situação-problema. Solicite que os alunos socializem seus registros de resolução e justifiquem seus procedimentos. Esses slides trazem possíveis soluções, porém explore as que forem apresentadas pelos alunos. Selecione alguns para registrarem suas estratégias no quadro, no flip chart ou numa folha de papel Kraft. Organize um painel de solução das duplas. Este procedimento de socializar os diferentes caminhos percorridos pelas duplas permite que cada aluno se aproprie de novas estratégias de solução para uma mesma situação-problema. Escolha um registro que não tenha sido concluído ou que não esteja totalmente correto pois, a partir da discussão da turma, os alunos terão que pensar mais para encontrarem os possíveis erros cometidos e encontrarem um jeito para alcançar a solução. Este painel de solução pode ser afixado na sala de aula servindo de apoio para novas discussões de outras situações-problema.
Observação: Não antecipe o momento dos alunos compartilharem suas descobertas, garanta que todos tenham o prazer de descobrir suas próprias soluções. Também não esqueça de valorizar a comunicação oral das crianças para que conheçam outras ideias e coloquem em jogo todo o conhecimento que já adquiriram.
Encerramento
Tempo sugerido: 3 minutos.
Propósito: Sintetizar as aprendizagens da aula.
Orientação: Retomar com a turma o que foi aprendido nesta aula.
Discuta com a turma:
- O tema foi fácil?
- Ficou alguma dúvida?
- Vocês conseguiram perceber que há várias maneiras de encontrar a terça parte de um todo, como, por exemplo, desenhos, decomposição dos números, adição de parcelas iguais, reta numerada, etc ?
Raio X
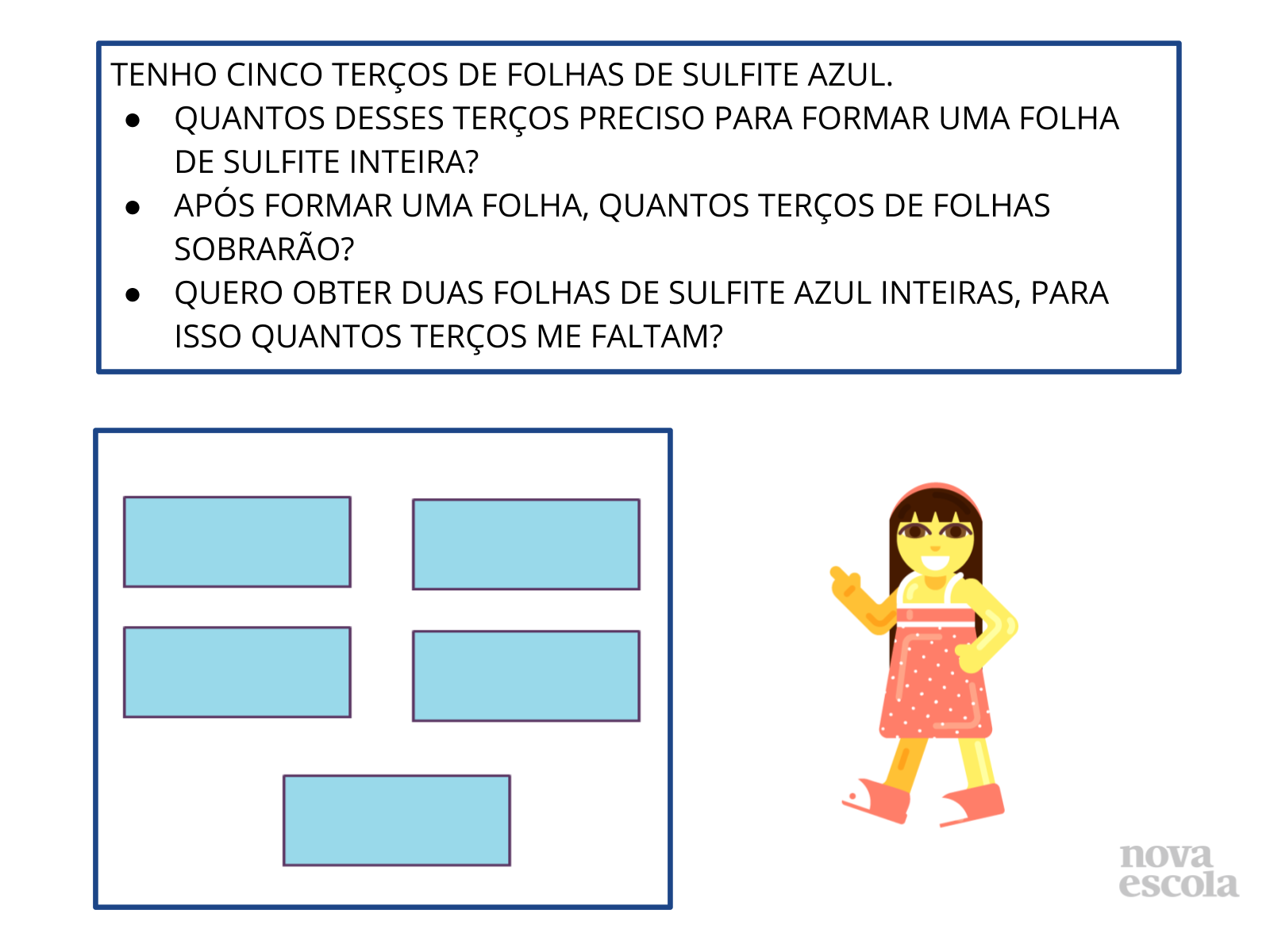
Tempo sugerido: 10 minutos.
Propósito: Verificar se os alunos compreenderam o que é terça parte de um todo.
Orientações: Solicite que os alunos, individualmente, leiam e realizem a atividade. Enquanto eles solucionam a situação-problema, circule pela sala e analise se os alunos demonstram, ao buscar a solução da atividade, ter compreendido o conceito de terça parte em relação ao todo. Observe quais os procedimentos que utilizam para resolver a atividade. Os alunos podem resolver a situação-problema usando um desenho para representar os cincos terços ou ter disponível a representação em folha de sulfite dos terços para manipular as partes e chegar a solução da situação-problema. Neste momento, não é esperado que os alunos utilizem operações de frações. O objetivo é que eles criem soluções inovadoras com significados plausíveis para a faixa etária em que se encontram. Proporcione na correção um momento que os alunos justifiquem seus procedimentos e avalie se será necessário realizar outras atividades para sistematizar a aprendizagem do conceito de terça parte.
Discuta com a turma:
- O que você irá fazer para descobrir quantos terços são necessários para formar uma folha de sulfite inteira?
- Explique quantos terços são precisos para formar duas folhas de sulfites inteiras?
Materiais Complementares:
Sugestão de adaptação para ensino remoto
Código do plano
MAT3_10NUM05
Recursos
- Necessários: estojo, papel ou caderno do aluno para que faça as anotações pertinentes.
Algum meio de comunicação com alunos: Zoom, Meet, WhatsApp, e-mail ou impressão.
Atividade principal.
- Opcionais:
Celular, computador ou tablet
Jogo: Carreira da divisão
Jogo: Divisões divertidas
Jogo físico: Divisão em linha
Grãos de feijão ou milho
Para este plano, foque na etapa da Atividade principal
Atividade principal
O foco desta atividade principal é a compreensão do conceito de terça-parte. O conceito de terça-parte foi apresentado para os alunos no segundo plano da sequência. Recomendamos que ele seja utilizado antes deste porque neste o grau de complexidade é um pouco maior. Os alunos precisam ter acesso à situação problema da atividade principal. Se você estiver em uma aula síncrona (Zoom, Meet…), pode apresentar o slide para os alunos e deixar que eles leiam a situação problema e a copiem no caderno. Caso não tenha aula síncrona, você não precisa utilizar o slide, pode colocar o enunciado em forma de texto ou áudio e compartilhar com os alunos via WhatsApp ou e-mail. Eles também devem copiar a situação no caderno. Os alunos podem desenhar o pedaço de tecido como está no slide para refletir e efetuar a divisão. Instigue os alunos para que percebam os elementos da situação problema e guiar um pouco as suas ações. Pergunte: através de texto ou áudio:
- Quantos centímetros tem o papel?
- Quantos cadernos dá para encapar com uma folha de 90 centímetros?
- Será que fazer um desenho ajuda a resolver?
- E usar a reta numerada, será que ajuda?
- Como seu colega pensou para resolver?
- Para encapar os 4 cadernos usaremos uma folha inteira ou precisamos de mais papel? Como podemos resolver isso?
- Estar em dupla facilitou para encontrar a resposta correta?
Dê um tempo para que os alunos realizem a atividade individualmente e oriente que eles podem representar sua resolução de formas variadas: cálculos, desenho, texto, fotografia, entretanto, devem saber explicá-las. Uma sugestão é separar previamente a turma em grupos fixos no Whatsapp para todas as atividades, dessa forma eles poderão compartilhar as suas estratégias com o grupo e debatê-las. No Zoom isso também é possível, você pode organizar salas separadas. Não se esqueça de entrar em todos os grupos para incentivá-los a trabalhar de forma produtiva no tempo estabelecido. Peça que os alunos compartilhem as suas resoluções e estratégias com os colegas, mantenham ou mudem de ideia. Depois, os alunos devem explicar como pensaram para realizar a atividade, quais estratégias usaram. A impressão e entrega da atividade também podem ser realizadas para os alunos que não têm acesso nenhum à Internet, entretanto, deve ser a última opção devido ao momento que estamos vivendo.
Painel de soluções
O painel de soluções é importante de ser compartilhado pois mostra de diversas formas como resolver o problema. Para isso, você pode tirar um print principalmente do slide 8 do painel que demonstra visualmente a solução da situação problema. Envie o print pela via de comunicação e interação que sua escola está utilizando. Os alunos podem escrever ou enviar áudios respondendo ou comentando as soluções encontradas, comparando-as com a forma que eles pensaram e solucionaram o problema. Promova um debate sadio entre os alunos.
Sistematização do conceito
É interessante que os alunos tenham a anotação do slide de sistematização em seus cadernos para consultas posteriores.
Raio X
A atividade do Raio X pode ser usada como tarefa de casa ou como avaliação da aula. Envie e faça a discussão da mesma forma que fez com a atividade principal. Lembre-se também que há atividades complementares que podem ser enviadas para os alunos como atividades de fixação ou sistematização.
Convite às famílias
Uma forma de envolvimento da família com os alunos nesta atividade é através de recursos utilizados no dia a dia, propondo a divisão de pizzas, bolos, tortas e através do compartilhamento de diferentes estratégias. Podem também incentivar os alunos a jogarem os jogos que foram indicados para a fixação da tabuada de divisão.
É interessante que os alunos envolvam as pessoas que estão ao seu redor em suas atividades escolares, mas devemos considerar que algumas vezes essas pessoas não poderão deixar seus afazeres e trabalhos para ajudá-los.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA.
Autor: Fátima Aparecida Marques Montesano
Mentor: Eliane Zanin
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
(EF03MA09) Associar o quociente de uma divisão com resto zero de um número natural por 2, 3, 4, 5 e 10 às ideias de metade, terça, quarta, quinta e décima partes.
Objetivos específicos
Aprimorar seus conhecimentos associados à ideia de terça parte com o todo.
Conceito-chave
Terça parte de um todo.
Conhecimentos prévios
Noção de dividir objetos e conjuntos de coisas em partes iguais;
em três partes; e os fatos básicos da adição.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não;
- Quadro ou flip chart para socialização dos registros;
- Projetor (opcional).