Atividade Principal
Plano de Aula
Plano de aula: Fatoração do trinômio quadrado perfeito com coeficiente dominante diferente de 1
Plano 6 de uma sequência de 10 planos. Veja todos os planos sobre Expressões algébricas e fatoração
Por: Vagner Campeão
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Vagner Campeão
Mentor: Telma Regina França Rosso
Especialista de área: Sandra Amorim
Habilidade da BNCC
EF09MA09: Compreender os processos de fatoração de expressões algébricas, com base em suas relações com os produtos notáveis, para resolver e elaborar problemas que possam ser representados por equações polinomiais do 2º grau.
Objetivos específicos
Resolver fatorações do tipo (bx + a)² estabelecendo relações com a expressão algébrica (bx)² + 2a(bx) +a² .
Conceito-chave
Fatoração de expressões algébricas
Conhecimentos que a turma deve dominar
Distributividade da multiplicação;
Cálculo de área de figuras retangulares;
Números quadrados perfeitos;
Recursos necessários
Projetor para apresentação dos slides da aula;
Atividades impressas em folhas, coladas no caderno ou não.
Régua;
Habilidades BNCC:
Objetivos de aprendizagem
Resolver fatorações do tipo (bx + a)² estabelecendo relações com a expressão algébrica (bx)² + 2a(bx) +a² .
Resumo da Aula
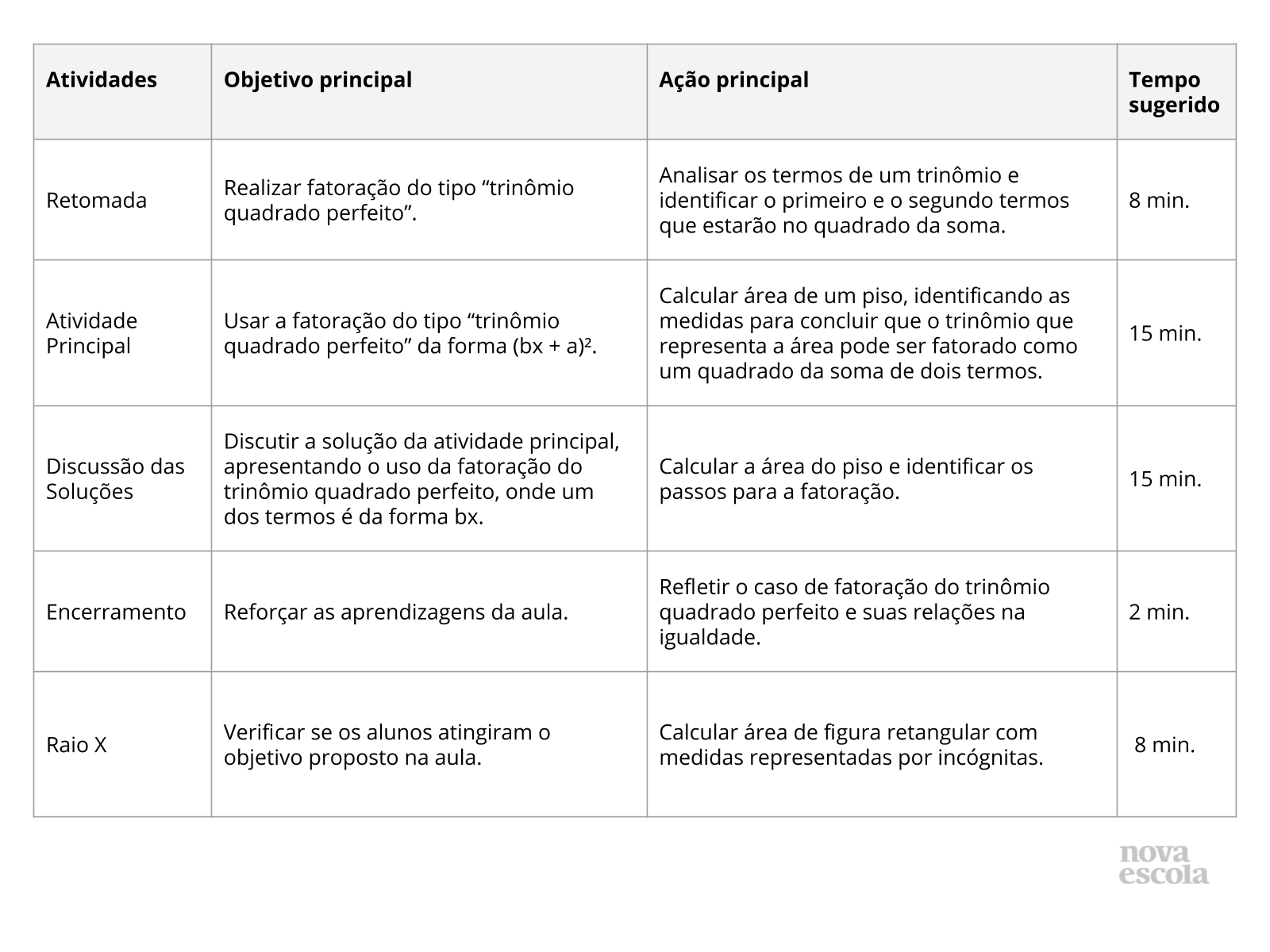 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia para os alunos o objetivo da aula.
Propósito: Apresentar o objetivo da aula.
Retomada

Tempo sugerido: 8 minutos. (Slides 3, 4 e 5)
Orientação: No slide 3, peça que, individualmente, os alunos leiam a atividade e escrevam suas respostas em seu caderno. Aproveite para retomar o conceito de fatoração. Espera-se como resposta: x² + 12x + 36 = (x + 6)².
Em seguida, no slide 4, realize coletivamente a leitura do slide, relembrando o conceito de trinômio quadrado perfeito.
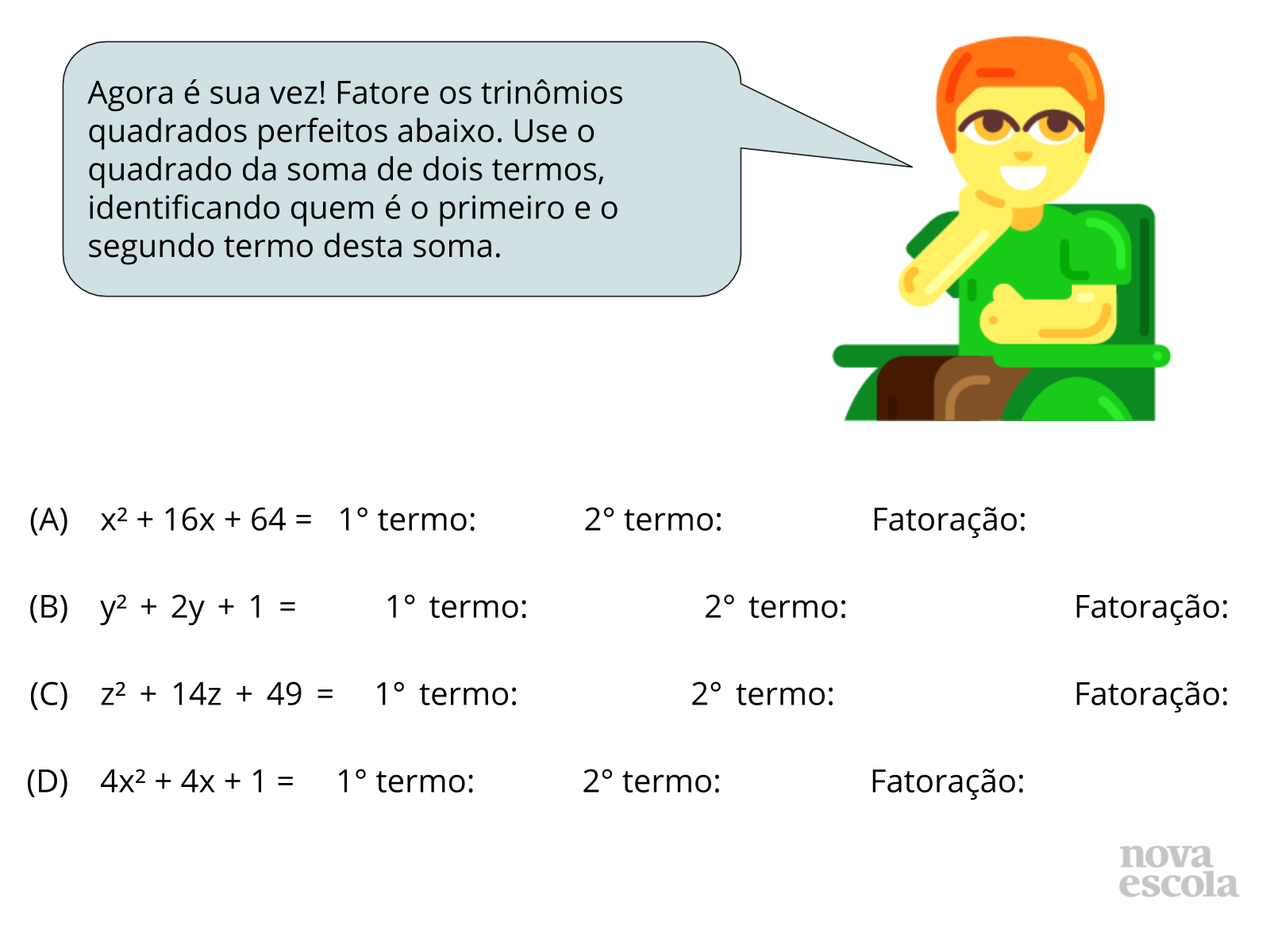
Após isto, proponha que os alunos resolvam a atividade de retomada. Sugira aos alunos que inicialmente encontrem o primeiro e depois o segundo termo. Com esses valores peça então que eles realizem a fatoração como o quadrado da soma desses dois termos encontrados.
Propósito: Retomar a fatoração por trinômio quadrado perfeito.
Discuta com a turma:
- O que é trinômio quadrado perfeito?
- O que o x² e o 36 tem em comum?
- De que forma podemos identificar que um trinômio é um quadrado perfeito?
Retomada

Tempo sugerido: 8 minutos. (Slides 3, 4 e 5)
Orientação: No slide 3, peça que, individualmente, os alunos leiam a atividade e escrevam suas respostas em seu caderno. Aproveite para retomar o conceito de fatoração. Espera-se como resposta: x² + 12x + 36 = (x + 6)².
Em seguida, no slide 4, realize coletivamente a leitura do slide, relembrando o conceito de trinômio quadrado perfeito.
Após isto, proponha que os alunos resolvam a atividade de retomada. Sugira aos alunos que inicialmente encontrem o primeiro e depois o segundo termo. Com esses valores peça então que eles realizem a fatoração como o quadrado da soma desses dois termos encontrados.
Propósito: Retomar a fatoração por trinômio quadrado perfeito.
Discuta com a turma:
- O que é trinômio quadrado perfeito?
- O que o x² e o 36 tem em comum?
- De que forma podemos identificar que um trinômio é um quadrado perfeito?
Retomada
Tempo sugerido: 8 minutos. (Slides 3, 4 e 5)
Orientação: No slide 3, peça que, individualmente, os alunos leiam a atividade e escrevam suas respostas em seu caderno. Aproveite para retomar o conceito de fatoração. Espera-se como resposta: x² + 12x + 36 = (x + 6)².
Em seguida, no slide 4, realize coletivamente a leitura do slide, relembrando o conceito de trinômio quadrado perfeito.
Após isto, proponha que os alunos resolvam a atividade de retomada. Sugira aos alunos que inicialmente encontrem o primeiro e depois o segundo termo. Com esses valores peça então que eles realizem a fatoração como o quadrado da soma desses dois termos encontrados.
Propósito: Retomar a fatoração por trinômio quadrado perfeito.
Discuta com a turma:
- O que é trinômio quadrado perfeito?
- O que o x² e o 36 tem em comum?
- De que forma podemos identificar que um trinômio é um quadrado perfeito?
Atividade Principal
Tempo sugerido: 15 minutos. (Slide 6 e 7)
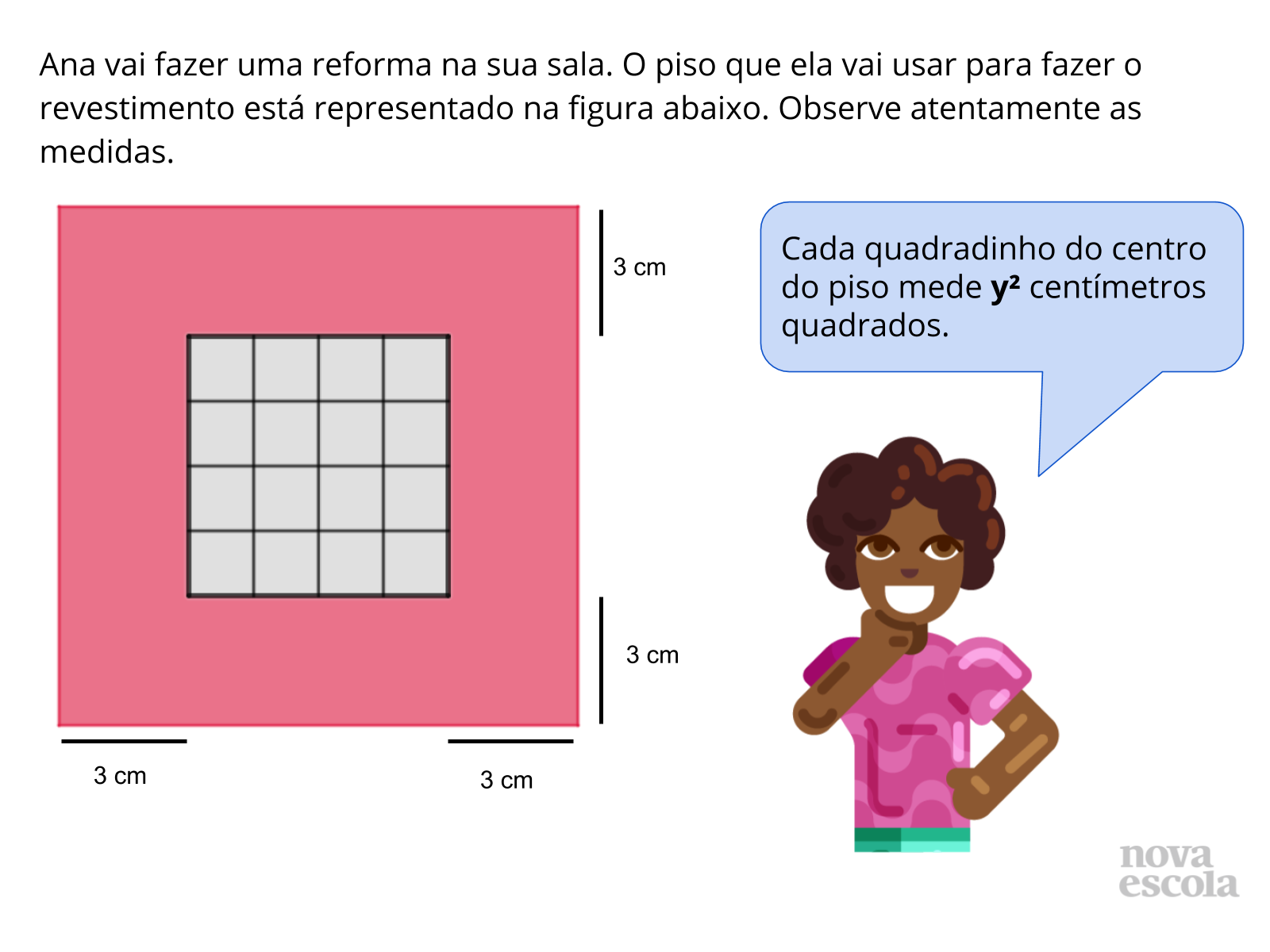
Orientação: Faça junto dos alunos uma leitura detalhada da situação problema. Chame a atenção deles para a observação que está no balão da personagem. Relembre aos alunos, se necessário, que se um quadrado possui área y² seus lados medirão y. Em seguida, deixe que os alunos pensem individualmente em como resolver a atividade e depois peça para que formem grupos de 3 a 4 pessoas.
Enquanto os alunos resolvem, procure observar as estratégias utilizadas por eles e também se há dúvidas ou dificuldades para começar a atividade, fazendo as intervenções necessárias. Consulte o guia de intervenção para mais informações.
Propósito: Explorar a fatoração de expressões algébricas do tipo (bx + a)² e relacioná-la à expressão (bx)² + 2a(bx) + a².
Discuta com a turma:
- Qual é a área central quadriculada deste piso?
- Quais outros quadrados podemos observar nessa figura?
- Quais medidas você encontrou para os lados do piso?
- Podemos dividir o piso em outros retângulos? De que forma?
- Que tipo de expressão algébrica é a que você encontrou para a área? Essa expressão pode ser fatorada?
Materiais complementares para impressão:
Atividade Principal
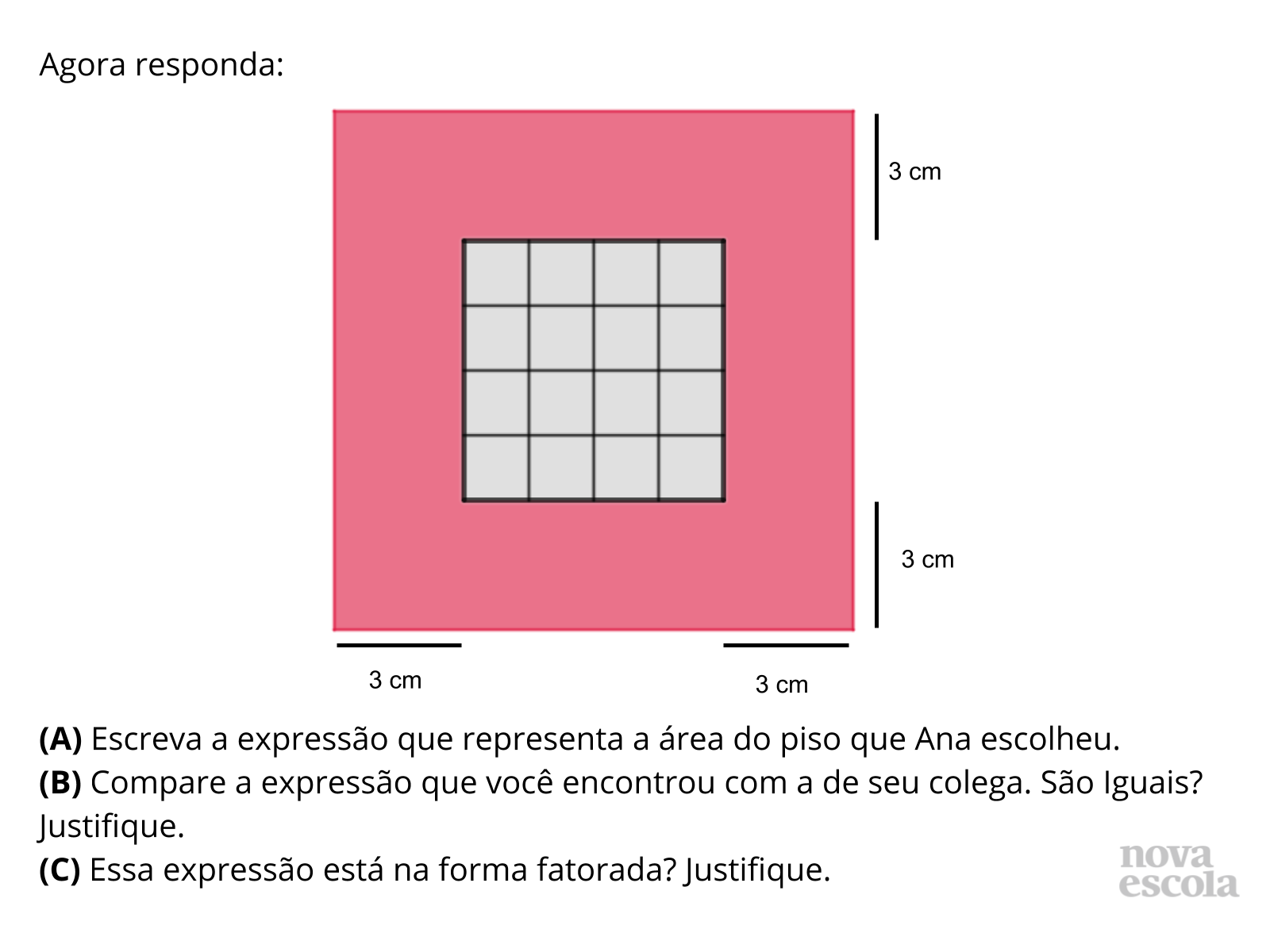
Tempo sugerido: 15 minutos. (Slide 6 e 7)
Orientação: Faça junto dos alunos uma leitura detalhada da situação problema. Chame a atenção deles para a observação que está no balão da personagem. Relembre aos alunos, se necessário, que se um quadrado possui área y² seus lados medirão y. Em seguida, deixe que os alunos pensem individualmente em como resolver a atividade e depois peça para que formem grupos de 3 a 4 pessoas.
Enquanto os alunos resolvem, procure observar as estratégias utilizadas por eles e também se há dúvidas ou dificuldades para começar a atividade, fazendo as intervenções necessárias. Consulte o guia de intervenção para mais informações.
Propósito: Explorar a fatoração de expressões algébricas do tipo (bx + a)² e relacioná-la à expressão (bx)² + 2a(bx) + a².
Discuta com a turma:
- Qual é a área central quadriculada deste piso?
- Quais outros quadrados podemos observar nessa figura?
- Quais medidas você encontrou para os lados do piso?
- Podemos dividir o piso em outros retângulos? De que forma?
- Que tipo de expressão algébrica é a que você encontrou para a área? Essa expressão pode ser fatorada?
Discussão das Soluções
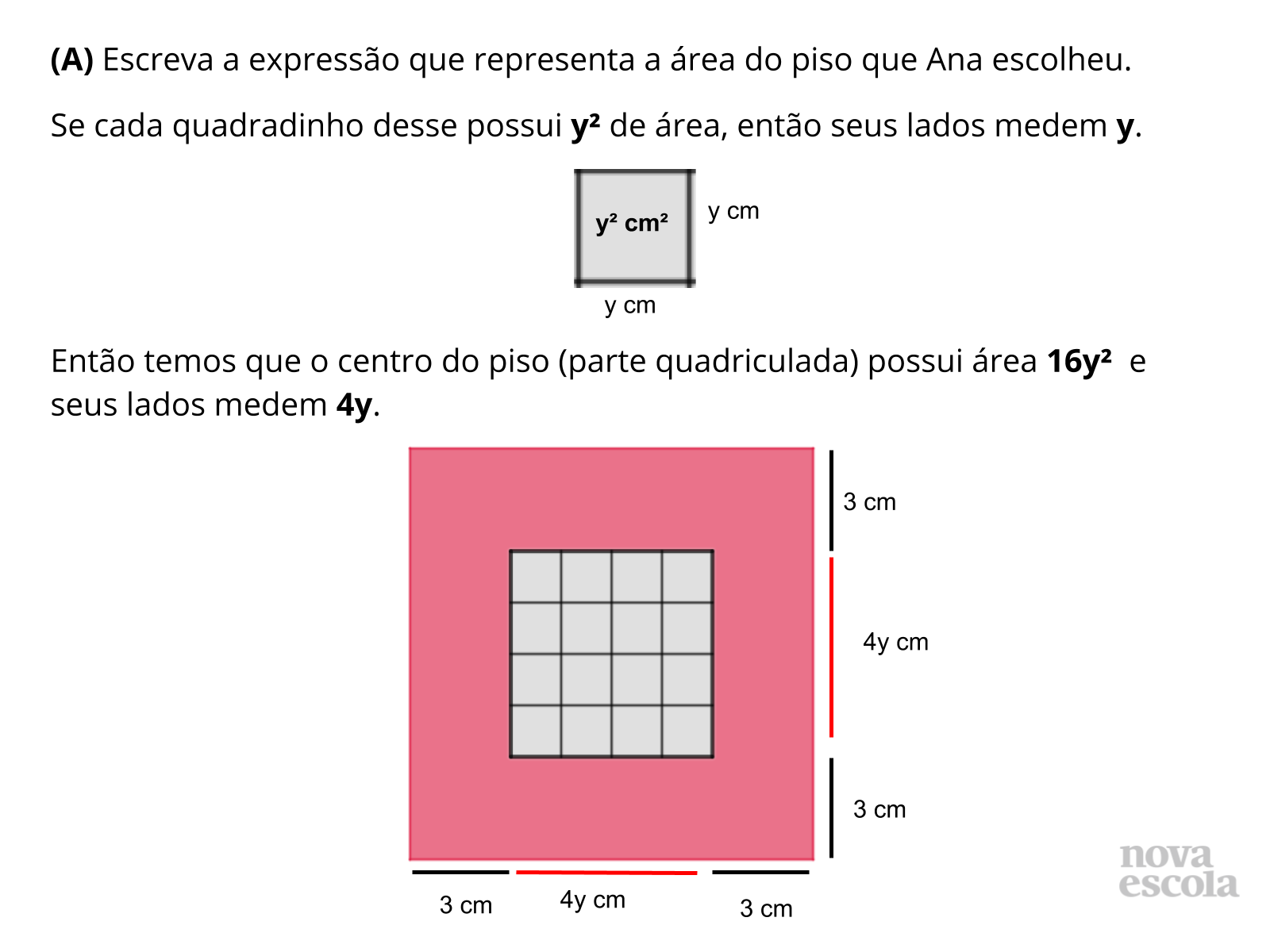
Tempo sugerido: 15 minutos. (slides 8 a 14)
Orientação: Inicie este momento da aula solicitando a um dos grupos de alunos que apresentem sua resolução para a atividade principal, ainda que você note erros, pois eles serão de grande importância. Após apresentarem, pergunte para a turma se há dúvidas ou se alguém resolveu de maneira semelhante. Caso detecte erros, faça perguntas aos alunos que os levem a entender o por que da resolução estar incorreta. Certifique-se que todos entenderam e então questione se outro grupo resolveu de maneira diferente, caso sim, peça para que também apresentem sua resolução. Feito isso, apresente então aos alunos a resolução presente nos slides de 8 a 14. Certifique-se de que todos entenderam e levante discussões, perguntando aos alunos: Qual destas resoluções apresentadas foi a mais fácil? E a mais prática? Vocês ainda possuem dúvida sobre algum procedimento utilizado? Qual?
Propósito: Explorar a fatoração de expressões algébricas do tipo (bx + a)² e relacioná-la à expressão (bx)² + 2a(bx) + a².
Discussão das Soluções
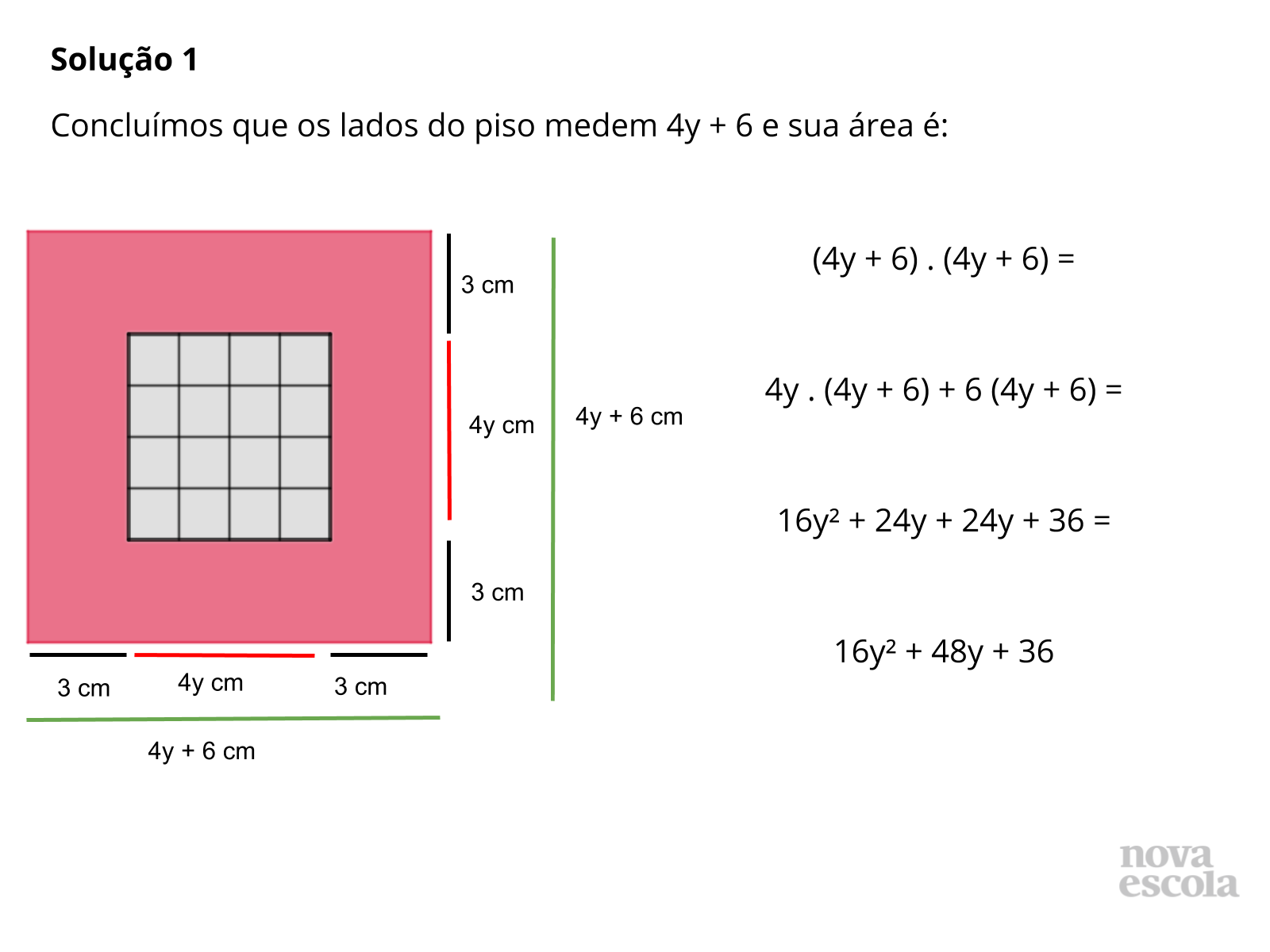
Tempo sugerido: 15 minutos. (slides 8 a 14)
Orientação: Inicie este momento da aula solicitando a um dos grupos de alunos que apresentem sua resolução para a atividade principal, ainda que você note erros, pois eles serão de grande importância. Após apresentarem, pergunte para a turma se há dúvidas ou se alguém resolveu de maneira semelhante. Caso detecte erros, faça perguntas aos alunos que os levem a entender o por que da resolução estar incorreta. Certifique-se que todos entenderam e então questione se outro grupo resolveu de maneira diferente, caso sim, peça para que também apresentem sua resolução. Feito isso, apresente então aos alunos a resolução presente nos slides de 8 a 14. Certifique-se de que todos entenderam e levante discussões, perguntando aos alunos: Qual destas resoluções apresentadas foi a mais fácil? E a mais prática? Vocês ainda possuem dúvida sobre algum procedimento utilizado? Qual?
Propósito: Explorar a fatoração de expressões algébricas do tipo (bx + a)² e relacioná-la à expressão (bx)² + 2a(bx) + a².
Discussão das Soluções
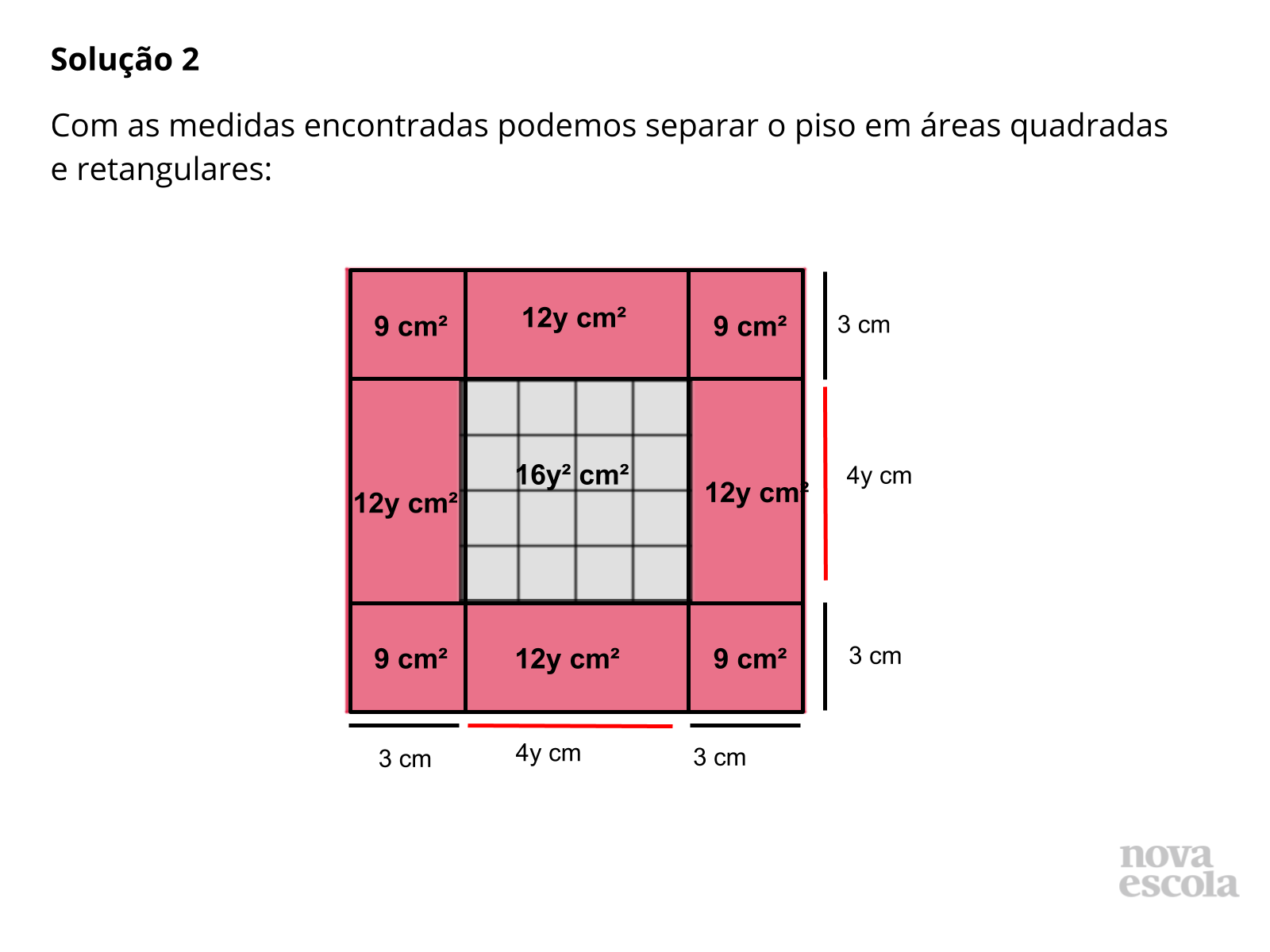
Tempo sugerido: 15 minutos. (slides 8 a 14)
Orientação: Inicie este momento da aula solicitando a um dos grupos de alunos que apresentem sua resolução para a atividade principal, ainda que você note erros, pois eles serão de grande importância. Após apresentarem, pergunte para a turma se há dúvidas ou se alguém resolveu de maneira semelhante. Caso detecte erros, faça perguntas aos alunos que os levem a entender o por que da resolução estar incorreta. Certifique-se que todos entenderam e então questione se outro grupo resolveu de maneira diferente, caso sim, peça para que também apresentem sua resolução. Feito isso, apresente então aos alunos a resolução presente nos slides de 8 a 14. Certifique-se de que todos entenderam e levante discussões, perguntando aos alunos: Qual destas resoluções apresentadas foi a mais fácil? E a mais prática? Vocês ainda possuem dúvida sobre algum procedimento utilizado? Qual?
Propósito: Explorar a fatoração de expressões algébricas do tipo (bx + a)² e relacioná-la à expressão (bx)² + 2a(bx) + a².
Discussão das Soluções

Tempo sugerido: 15 minutos. (slides 8 a 14)
Orientação: Inicie este momento da aula solicitando a um dos grupos de alunos que apresentem sua resolução para a atividade principal, ainda que você note erros, pois eles serão de grande importância. Após apresentarem, pergunte para a turma se há dúvidas ou se alguém resolveu de maneira semelhante. Caso detecte erros, faça perguntas aos alunos que os levem a entender o por que da resolução estar incorreta. Certifique-se que todos entenderam e então questione se outro grupo resolveu de maneira diferente, caso sim, peça para que também apresentem sua resolução. Feito isso, apresente então aos alunos a resolução presente nos slides de 8 a 14. Certifique-se de que todos entenderam e levante discussões, perguntando aos alunos: Qual destas resoluções apresentadas foi a mais fácil? E a mais prática? Vocês ainda possuem dúvida sobre algum procedimento utilizado? Qual?
Propósito: Explorar a fatoração de expressões algébricas do tipo (bx + a)² e relacioná-la à expressão (bx)² + 2a(bx) + a².
Discussão das Soluções

Tempo sugerido: 15 minutos. (slides 8 a 14)
Orientação: Inicie este momento da aula solicitando a um dos grupos de alunos que apresentem sua resolução para a atividade principal, ainda que você note erros, pois eles serão de grande importância. Após apresentarem, pergunte para a turma se há dúvidas ou se alguém resolveu de maneira semelhante. Caso detecte erros, faça perguntas aos alunos que os levem a entender o por que da resolução estar incorreta. Certifique-se que todos entenderam e então questione se outro grupo resolveu de maneira diferente, caso sim, peça para que também apresentem sua resolução. Feito isso, apresente então aos alunos a resolução presente nos slides de 8 a 14. Certifique-se de que todos entenderam e levante discussões, perguntando aos alunos: Qual destas resoluções apresentadas foi a mais fácil? E a mais prática? Vocês ainda possuem dúvida sobre algum procedimento utilizado? Qual?
Propósito: Explorar a fatoração de expressões algébricas do tipo (bx + a)² e relacioná-la à expressão (bx)² + 2a(bx) + a².
Discussão das Soluções

Tempo sugerido: 15 minutos. (slides 8 a 14)
Orientação: Inicie este momento da aula solicitando a um dos grupos de alunos que apresentem sua resolução para a atividade principal, ainda que você note erros, pois eles serão de grande importância. Após apresentarem, pergunte para a turma se há dúvidas ou se alguém resolveu de maneira semelhante. Caso detecte erros, faça perguntas aos alunos que os levem a entender o por que da resolução estar incorreta. Certifique-se que todos entenderam e então questione se outro grupo resolveu de maneira diferente, caso sim, peça para que também apresentem sua resolução. Feito isso, apresente então aos alunos a resolução presente nos slides de 8 a 14. Certifique-se de que todos entenderam e levante discussões, perguntando aos alunos: Qual destas resoluções apresentadas foi a mais fácil? E a mais prática? Vocês ainda possuem dúvida sobre algum procedimento utilizado? Qual?
Propósito: Explorar a fatoração de expressões algébricas do tipo (bx + a)² e relacioná-la à expressão (bx)² + 2a(bx) + a².
Discussão das Soluções
Tempo sugerido: 15 minutos. (slides 8 a 14)
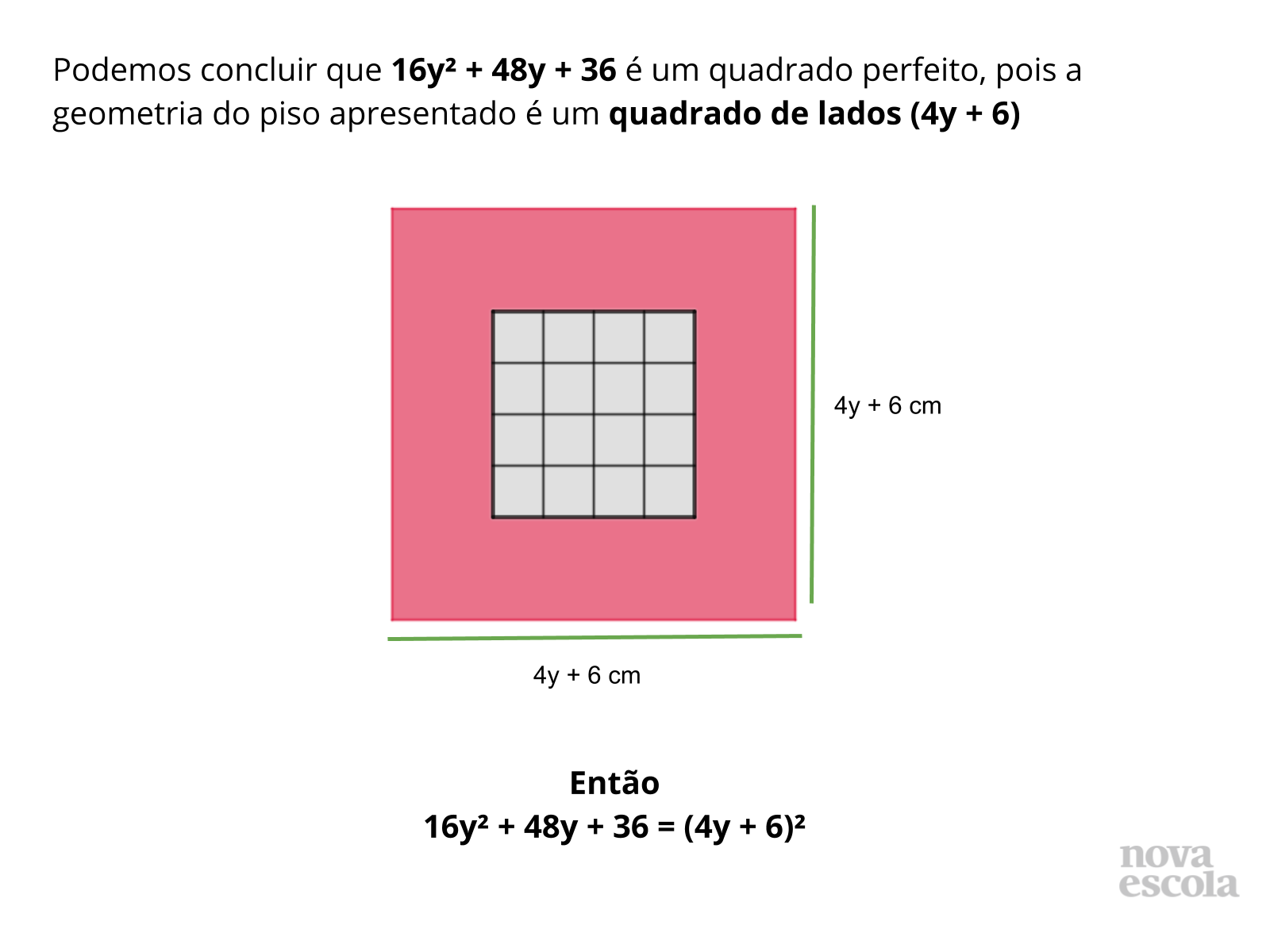
Orientação: Inicie este momento da aula solicitando a um dos grupos de alunos que apresentem sua resolução para a atividade principal, ainda que você note erros, pois eles serão de grande importância. Após apresentarem, pergunte para a turma se há dúvidas ou se alguém resolveu de maneira semelhante. Caso detecte erros, faça perguntas aos alunos que os levem a entender o por que da resolução estar incorreta. Certifique-se que todos entenderam e então questione se outro grupo resolveu de maneira diferente, caso sim, peça para que também apresentem sua resolução. Feito isso, apresente então aos alunos a resolução presente nos slides de 8 a 14. Certifique-se de que todos entenderam e levante discussões, perguntando aos alunos: Qual destas resoluções apresentadas foi a mais fácil? E a mais prática? Vocês ainda possuem dúvida sobre algum procedimento utilizado? Qual?
Propósito: Explorar a fatoração de expressões algébricas do tipo (bx + a)² e relacioná-la à expressão (bx)² + 2a(bx) + a².
Encerramento

Tempo sugerido: 2 minutos
Orientação: Neste momento, procure destacar as principais aprendizagens da aula:
- Identificação de trinômios quadrados perfeitos, nos quais um dos termos é o produto de um número por uma incógnita, do tipo (bx).
- Quando esses trinômios estudados são fatorados, tornam-se o quadrado da soma de dois termos.
Propósito: Reforçar as aprendizagens da aula.
Raio X
Tempo sugerido: 8 minutos. (slides 16 e 17)
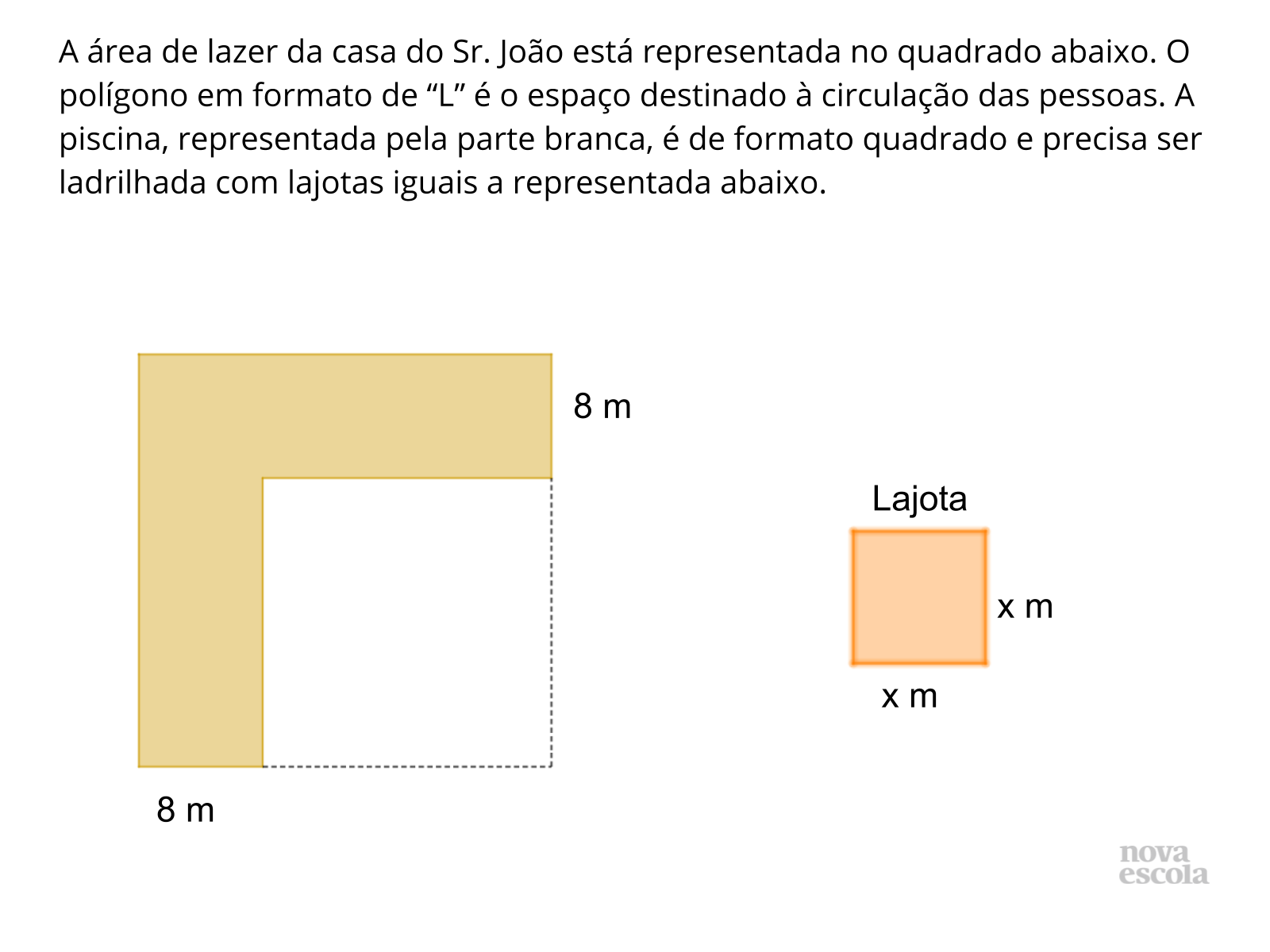
Orientação: Peça para que os alunos leiam e respondam a atividade de raio x individualmente. Sugira que usem a fatoração do trinômio quadrado perfeito do tipo (bx + a)². A atividade de raio x trata-se de um importante momento de avaliação, aproveite enquanto os alunos respondem a atividade para observar como eles estão resolvendo e se ainda há dúvidas ou dificuldades, para que as devidas intervenções sejam feitas e se necessário, você possa indicá-los a resolver as atividades complementares, disponíveis logo abaixo.
Propósito: Avaliar a aprendizagem dos alunos quanto à fatoração do trinômio quadrado perfeito.
Discuta com a turma:
- Como você pode associar os termos do trinômio encontrado com as regiões da área de lazer?
- Quais outras expressões equivalentes podem ser utilizadas?
Materiais complementares para impressão:
Raio X
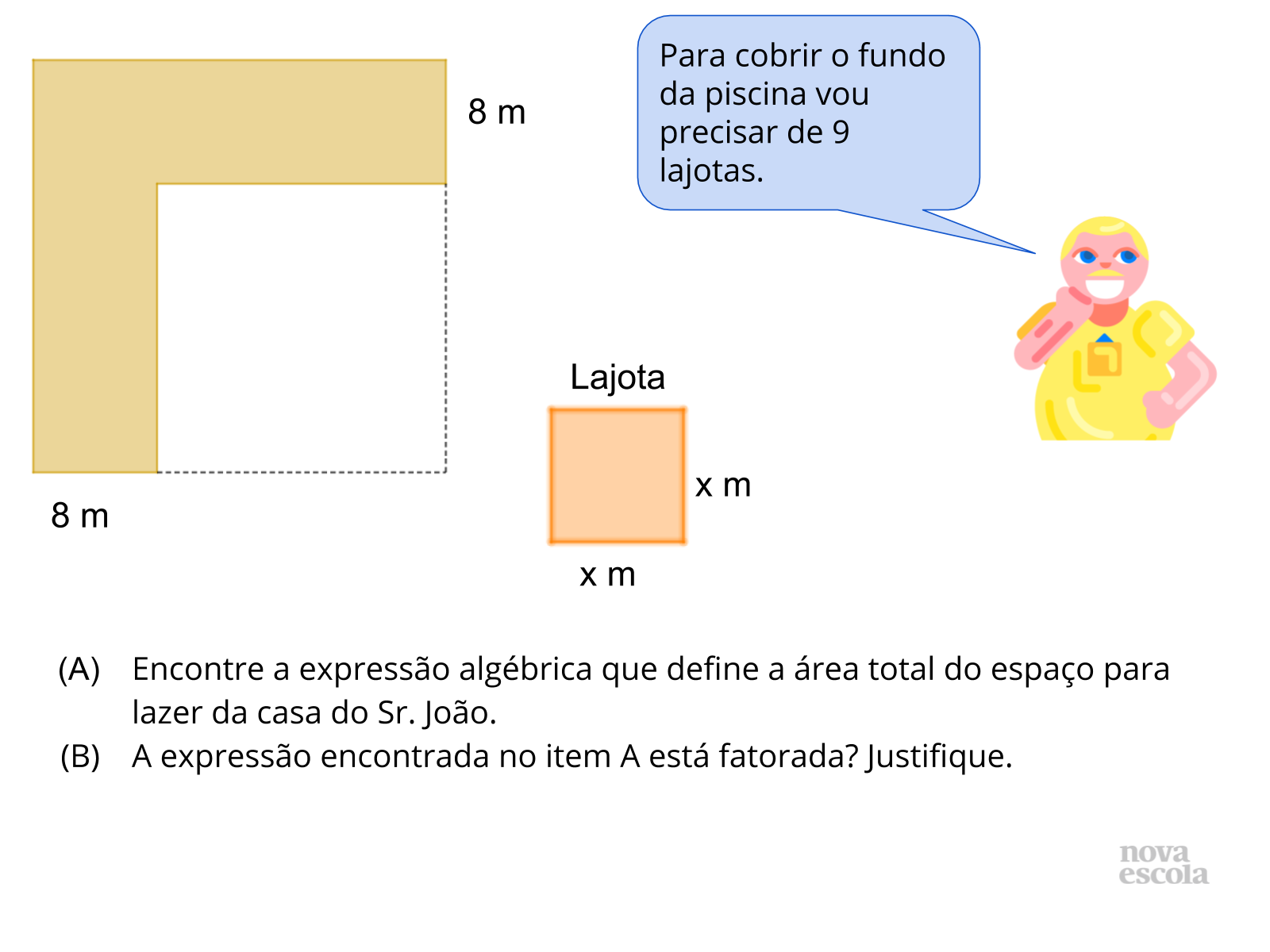
Tempo sugerido: 8 minutos. (slides 16 e 17)
Orientação: Peça para que os alunos leiam e respondam a atividade de raio x individualmente. Sugira que usem a fatoração do trinômio quadrado perfeito do tipo (bx + a)². A atividade de raio x trata-se de um importante momento de avaliação, aproveite enquanto os alunos respondem a atividade para observar como eles estão resolvendo e se ainda há dúvidas ou dificuldades, para que as devidas intervenções sejam feitas e se necessário, você possa indicá-los a resolver as atividades complementares, disponíveis logo abaixo.
Propósito: Avaliar a aprendizagem dos alunos quanto à fatoração do trinômio quadrado perfeito.
Discuta com a turma:
- Como você pode associar os termos do trinômio encontrado com as regiões da área de lazer?
- Quais outras expressões equivalentes podem ser utilizadas?
Para os alunos
Para o professor
Sugestão de adaptação para ensino remoto
Código do plano (MAT9_05ALG06)
Ferramentas sugeridas
- Essenciais: Alguma rede social (Whatsapp, Facebook, etc.) e papel para anotações, régua.
- Optativas: Calculadora e tesoura.
Aquecimento
- Pela rede social escolhida, peça que relembrem sobre como se fatora a expressão: a² + 2. a.b + b². Lembrando que é um produto notável e necessita uma atenção por ser de mais fácil percepção do que outros casos.
Atividade principal
- Proponha uma pesquisa (em livros ou na internet), determinando um prazo para a entrega, de situações-problema que podem gerar o produto notável
(a + b)² que envolvem superfícies. E, na entrega, peça que descrevam ou mostrem as correspondentes geométricas das expressões geradas.
Painel e discussão de soluções
Depende das respostas. Mas conduza de forma a perceberem a força do uso de um produto notável como ferramenta de cálculo
Sistematização e encerramento
- Faça uma sistematização dizendo que o produto notável (a + b)² deve ser visto de forma que o termo a e b possam ainda ser formados por monômios que apresentam a parte numérica diferente de 1. Ex.: (2x + 3y)² = 4x² + 12x.y + 9y²; pois o a=2x e b=3y.
Raio X
Sugira que desenvolvam a expressão: (3x + 5y)² = ?
Convite às famílias
Peça para que seus alunos envolvam seus familiares, próximos neste momento, a pesquisarem as situações ou sugerirem situações para o uso das expressões do tipo (a + b)².
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Vagner Campeão
Mentor: Telma Regina França Rosso
Especialista de área: Sandra Amorim
Habilidade da BNCC
EF09MA09: Compreender os processos de fatoração de expressões algébricas, com base em suas relações com os produtos notáveis, para resolver e elaborar problemas que possam ser representados por equações polinomiais do 2º grau.
Objetivos específicos
Resolver fatorações do tipo (bx + a)² estabelecendo relações com a expressão algébrica (bx)² + 2a(bx) +a² .
Conceito-chave
Fatoração de expressões algébricas
Conhecimentos que a turma deve dominar
Distributividade da multiplicação;
Cálculo de área de figuras retangulares;
Números quadrados perfeitos;
Recursos necessários
Projetor para apresentação dos slides da aula;
Atividades impressas em folhas, coladas no caderno ou não.
Régua;