Atividade principal
Plano de Aula
Plano de aula: Quadriláteros: trapézio isósceles e paralelogramo
Plano 1 de uma sequência de 10 planos. Veja todos os planos sobre Propriedades de quadriláteros
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Geisa Zilli Shinkawa da Silva
Mentor: Vinícius do Nascimento Silva Mano e Fabricio Eduardo Ferreira
Especialista de área: Priscilla Cerqueira
Habilidade da BNCC
EF08MA12 - Demonstrar as propriedades de quadriláteros por meio da identificação da congruência de triângulos.
Objetivos específicos
- Deduzir as propriedades dos paralelogramos utilizando congruência de triângulos;
- Deduzir as propriedades dos trapézios isósceles utilizando congruência de triângulos;
- Reconhecer as principais características dos quadriláteros e suas propriedades.
Conceito-chave
Propriedades de quadriláteros.
Recursos necessários
- Lápis de escrever, lápis de cor, borracha e tesoura;
- Esquadros e régua;
- Folha de papel A4 (para desenho e recorte);
- Atividades impressas em folhas ou projetadas.
Habilidades BNCC:
Objetivos de aprendizagem
- Deduzir as propriedades dos paralelogramos utilizando congruência de triângulos;
- Deduzir as propriedades dos trapézios isósceles utilizando congruência de triângulos;
- Reconhecer as principais características dos quadriláteros e suas propriedades.
Resumo da aula
Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar a proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Leitura individual ou leitura compartilhada junto com os estudantes para deixar claro o objetivo da aula.
Propósito: Compartilhar o objetivo da aula com os alunos
Aquecimento

Tempo sugerido: 5 minutos (Slides 3 e 4).
Orientação: Por meio de roda de conversa, deixando os estudantes o mais à vontade possível, inicie os questionamentos e sistematize no quadro algumas respostas dadas por eles, de modo a retomá-las ao final da aula, para refutá-las ou validá-las.
Propósito: Sensibilizar o aluno para a proposta da aula e ativar seus conhecimentos prévios sobre quadriláteros e congruências de triângulos.
Discuta com a turma:
- O que são quadriláteros? Quais as suas principais características?
- Onde esses quadriláteros são vistos/utilizados?
- Você se lembra dos casos de congruência de triângulos?
Aquecimento

Tempo sugerido: 5 minutos (Slides 3 e 4).
Orientação: Por meio de roda de conversa, deixando os estudantes o mais à vontade possível, inicie os questionamentos e sistematize no quadro algumas respostas dadas por eles, de modo a retomá-las ao final da aula, para refutá-las ou validá-las.
Propósito: Sensibilizar o aluno para a proposta da aula e ativar seus conhecimentos prévios sobre quadriláteros e congruências de triângulos.
Discuta com a turma:
- O que são quadriláteros? Quais as suas principais características?
- Onde esses quadriláteros são vistos/utilizados?
- Você se lembra dos casos de congruência de triângulos?
Atividade Principal
Tempo sugerido: 18 minutos (Slides 5 a 8)
Orientação:
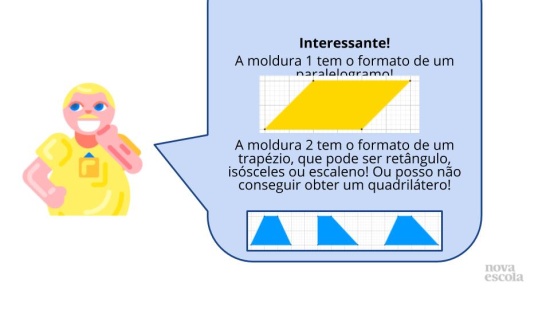
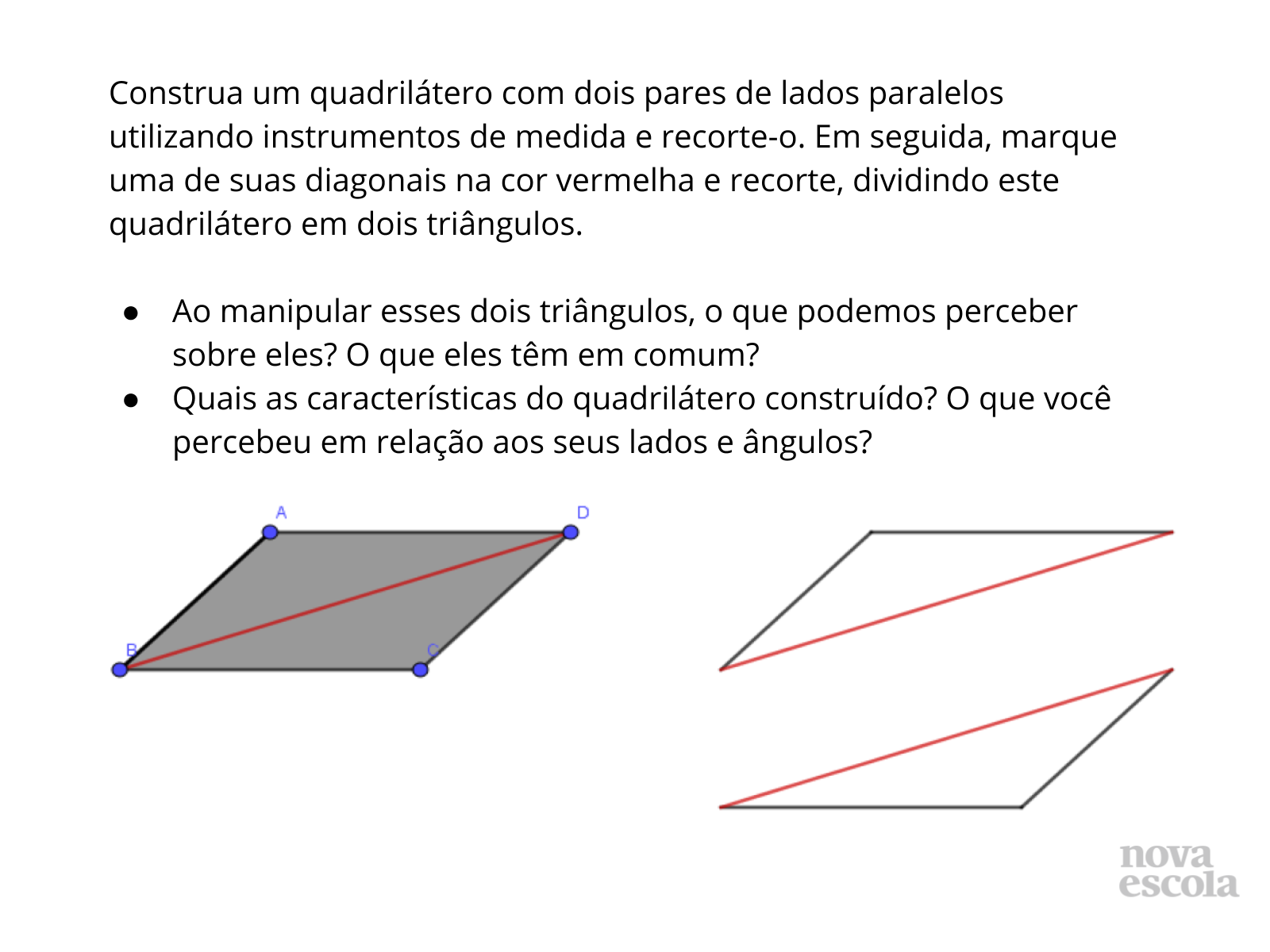
No slide 5, peça aos estudantes que construam o quadrilátero solicitado utilizando esquadros e que escolham as medidas que acharem convenientes para os lados, de modo a valorizar diferentes figuras, ou seja, figuras com diversas dimensões. Após recortarem, peça aos alunos que manipulem os triângulos e que busquem observar as características referentes aos seus lados e ângulos. Caso não percebam, atente-os para o fato de que é possível sobrepor as figuras e que elas são congruentes.
No slide 6, faça os questionamentos aos alunos e permita que eles discutam entre si o que perceberam que há de relação entre os lados opostos de um paralelogramo. Para conduzir suas conclusões, você também pode fazer os questionamentos do item “Discuta com a turma”, logo abaixo.
No slide 7, permita inicialmente que os alunos manipulem as formas construídas e recortadas, sobrepondo-as, colocando lado a lado, rotacionando-as, entre outros movimentos. Em seguida, faça os questionamentos presentes no slide.
Após explorar as observações feitas pelos alunos, caso eles não tenham notado nem compartilhado ainda, oriente-os que ao sobrepor as partes obtidas nos recortes, algumas delas se “encaixam” perfeitamente, e por consequência, representarão lados (ou diagonais) com mesma medida. Você pode também pegar as figuras de algum deles e mostrar para todos esta informação.
No slide 8, faça os questionamentos apresentados e, caso os alunos não cheguem às conclusões desejada, de que todo “trapézio isósceles possui os lados não paralelos com mesma medida e os ângulos adjacentes à mesma base também com mesma medida” faça os questionamentos do item “Discuta com a turma”, trocando a palavra paralelogramo por trapézio.
Propósito: Conduzir a discussão com os alunos para que eles sistematizem as propriedades: “em um paralelogramo, os lados opostos são congruentes”, “todo trapézio possui um par de lados paralelos” e também que “em todo trapézio isósceles os lados não paralelos possuem a mesma medida e os ângulos adjacentes à mesma base também possuem a mesma medida”
Discuta com a turma:
- O que podemos observar ao sobrepor as partes que encontramos? Elas se “encaixam” perfeitamente?
- O que isso significa em relação aos lados do paralelogramo? E aos ângulos?
- Como relacionar a congruência de triângulos e as propriedades dos paralelogramos?
Materiais Complementares:
Resolução da atividade principal
Atividade Principal

Tempo sugerido: 18 minutos (Slides 5 a 8)
Orientação:
No slide 5, peça aos estudantes que construam o quadrilátero solicitado utilizando esquadros e que escolham as medidas que acharem convenientes para os lados, de modo a valorizar diferentes figuras, ou seja, figuras com diversas dimensões. Após recortarem, peça aos alunos que manipulem os triângulos e que busquem observar as características referentes aos seus lados e ângulos. Caso não percebam, atente-os para o fato de que é possível sobrepor as figuras e que elas são congruentes.
No slide 6, faça os questionamentos aos alunos e permita que eles discutam entre si o que perceberam que há de relação entre os lados opostos de um paralelogramo. Para conduzir suas conclusões, você também pode fazer os questionamentos do item “Discuta com a turma”, logo abaixo.
No slide 7, permita inicialmente que os alunos manipulem as formas construídas e recortadas, sobrepondo-as, colocando lado a lado, rotacionando-as, entre outros movimentos. Em seguida, faça os questionamentos presentes no slide.
Após explorar as observações feitas pelos alunos, caso eles não tenham notado nem compartilhado ainda, oriente-os que ao sobrepor as partes obtidas nos recortes, algumas delas se “encaixam” perfeitamente, e por consequência, representarão lados (ou diagonais) com mesma medida. Você pode também pegar as figuras de algum deles e mostrar para todos esta informação.
No slide 8, faça os questionamentos apresentados e, caso os alunos não cheguem às conclusões desejada, de que todo “trapézio isósceles possui os lados não paralelos com mesma medida e os ângulos adjacentes à mesma base também com mesma medida” faça os questionamentos do item “Discuta com a turma”, trocando a palavra paralelogramo por trapézio.
Propósito: Conduzir a discussão com os alunos para que eles sistematizam as propriedades: “em um paralelogramo, os lados opostos são congruentes”, “todo trapézio possui um par de lados paralelos” e também que “em todo trapézio isósceles os lados não paralelos possuem a mesma medida e os ângulos adjacentes à mesma base também possuem a mesma medida”
Discuta com a turma:
- O que podemos observar ao sobrepor as partes que encontramos? Elas se “encaixam” perfeitamente?
- O que isso significa em relação aos lados do paralelogramo? E aos ângulos?
- Como relacionar a congruência de triângulos e as propriedades dos paralelogramos?
Atividade Principal
Tempo sugerido: 18 minutos (Slides 5 a 8)
Orientação:
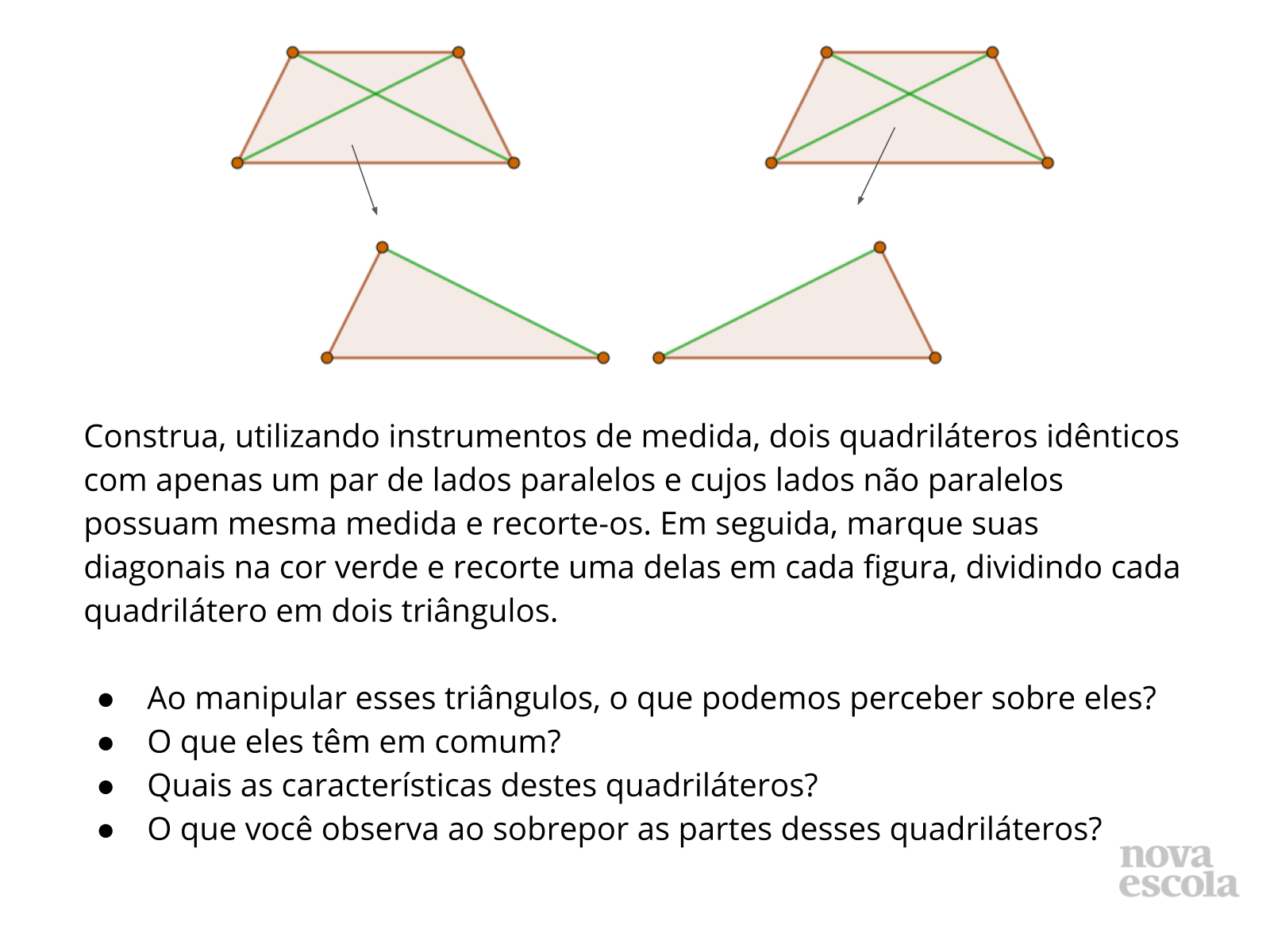
No slide 5, peça aos estudantes que construam o quadrilátero solicitado utilizando esquadros e que escolham as medidas que acharem convenientes para os lados, de modo a valorizar diferentes figuras, ou seja, figuras com diversas dimensões. Após recortarem, peça aos alunos que manipulem os triângulos e que busquem observar as características referentes aos seus lados e ângulos. Caso não percebam, atente-os para o fato de que é possível sobrepor as figuras e que elas são congruentes.
No slide 6, faça os questionamentos aos alunos e permita que eles discutam entre si o que perceberam que há de relação entre os lados opostos de um paralelogramo. Para conduzir suas conclusões, você também pode fazer os questionamentos do item “Discuta com a turma”, logo abaixo.
No slide 7, permita inicialmente que os alunos manipulem as formas construídas e recortadas, sobrepondo-as, colocando lado a lado, rotacionando-as, entre outros movimentos. Em seguida, faça os questionamentos presentes no slide.
Após explorar as observações feitas pelos alunos, caso eles não tenham notado nem compartilhado ainda, oriente-os que ao sobrepor as partes obtidas nos recortes, algumas delas se “encaixam” perfeitamente, e por consequência, representarão lados (ou diagonais) com mesma medida. Você pode também pegar as figuras de algum deles e mostrar para todos esta informação.
No slide 8, faça os questionamentos apresentados e, caso os alunos não cheguem às conclusões desejada, de que todo “trapézio isósceles possui os lados não paralelos com mesma medida e os ângulos adjacentes à mesma base também com mesma medida” faça os questionamentos do item “Discuta com a turma”, trocando a palavra paralelogramo por trapézio.
Propósito: Conduzir a discussão com os alunos para que eles sistematizam as propriedades: “em um paralelogramo, os lados opostos são congruentes”, “todo trapézio possui um par de lados paralelos” e também que “em todo trapézio isósceles os lados não paralelos possuem a mesma medida e os ângulos adjacentes à mesma base também possuem a mesma medida”
Discuta com a turma:
- O que podemos observar ao sobrepor as partes que encontramos? Elas se “encaixam” perfeitamente?
- O que isso significa em relação aos lados do paralelogramo? E aos ângulos?
- Como relacionar a congruência de triângulos e as propriedades dos paralelogramos?
Atividade Principal

Tempo sugerido: 18 minutos (Slides 5 a 8)
Orientação:
No slide 5, peça aos estudantes que construam o quadrilátero solicitado utilizando esquadros e que escolham as medidas que acharem convenientes para os lados, de modo a valorizar diferentes figuras, ou seja, figuras com diversas dimensões. Após recortarem, peça aos alunos que manipulem os triângulos e que busquem observar as características referentes aos seus lados e ângulos. Caso não percebam, atente-os para o fato de que é possível sobrepor as figuras e que elas são congruentes.
No slide 6, faça os questionamentos aos alunos e permita que eles discutam entre si o que perceberam que há de relação entre os lados opostos de um paralelogramo. Para conduzir suas conclusões, você também pode fazer os questionamentos do item “Discuta com a turma”, logo abaixo.
No slide 7, permita inicialmente que os alunos manipulem as formas construídas e recortadas, sobrepondo-as, colocando lado a lado, rotacionando-as, entre outros movimentos. Em seguida, faça os questionamentos presentes no slide.
Após explorar as observações feitas pelos alunos, caso eles não tenham notado nem compartilhado ainda, oriente-os que ao sobrepor as partes obtidas nos recortes, algumas delas se “encaixam” perfeitamente, e por consequência, representarão lados (ou diagonais) com mesma medida. Você pode também pegar as figuras de algum deles e mostrar para todos esta informação.
No slide 8, faça os questionamentos apresentados e, caso os alunos não cheguem às conclusões desejada, de que todo “trapézio isósceles possui os lados não paralelos com mesma medida e os ângulos adjacentes à mesma base também com mesma medida” faça os questionamentos do item “Discuta com a turma”, trocando a palavra paralelogramo por trapézio.
Propósito: Conduzir a discussão com os alunos para que eles sistematizem as propriedades: “em um paralelogramo, os lados opostos são congruentes”, “todo trapézio possui um par de lados paralelos” e também que “em todo trapézio isósceles os lados não paralelos possuem a mesma medida e os ângulos adjacentes à mesma base também possuem a mesma medida”
Discuta com a turma:
- O que podemos observar ao sobrepor as partes que encontramos? Elas se “encaixam” perfeitamente?
- O que isso significa em relação aos lados do paralelogramo? E aos ângulos?
- Como relacionar a congruência de triângulos e as propriedades dos paralelogramos?
Discussão das Soluções
Tempo sugerido: 10 minutos (Slides 9 a 11).
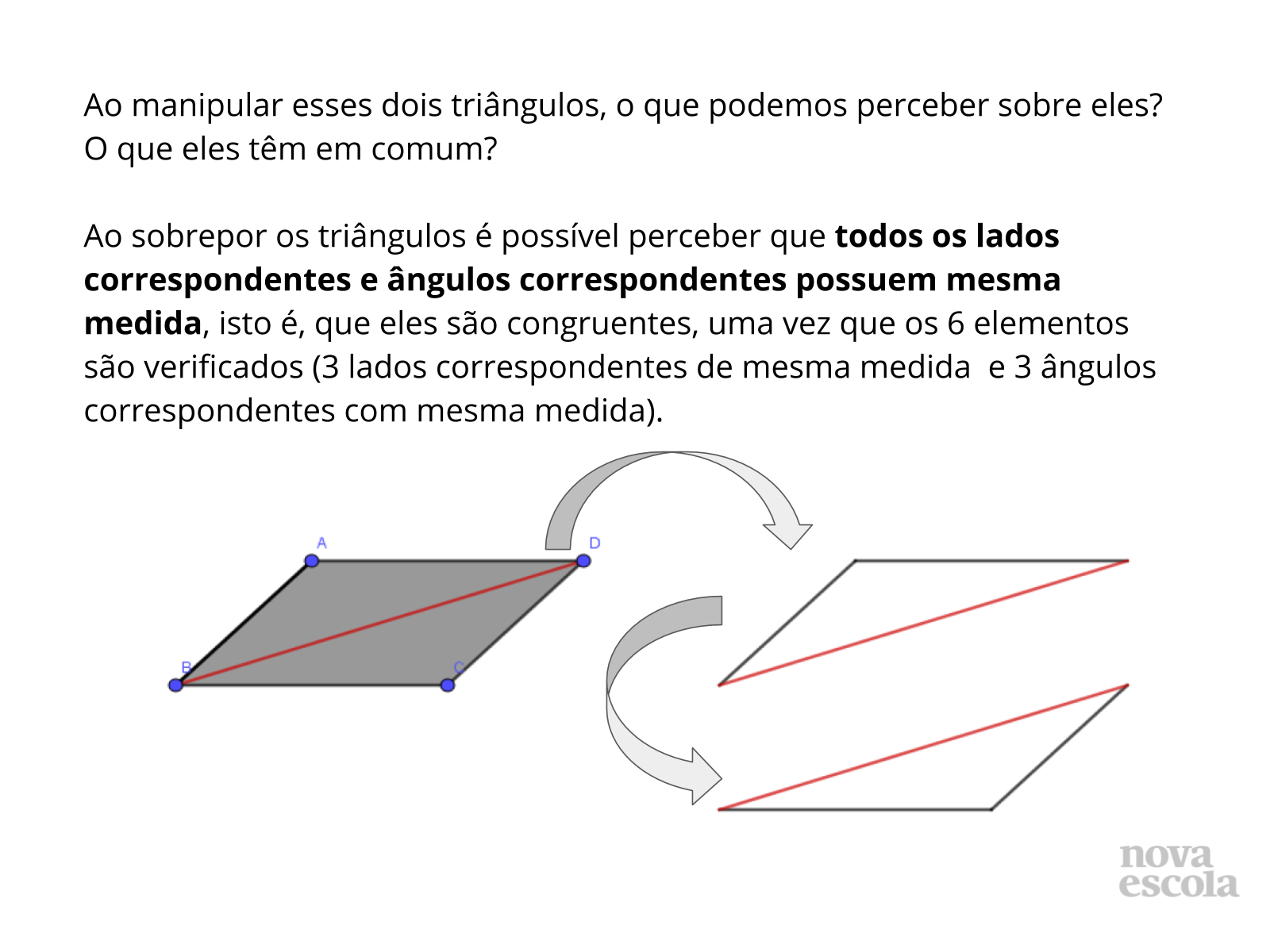
Orientação: Como as descobertas já ocorreram durante a construção e manipulação da figura, espera-se que nesta parte haja a sistematização do que foi trabalhado ao longo da atividade, apresentando os estudantes a uma definição formal dos conceitos. Pode ser realizada leitura compartilhada, com manipulação das figuras de modo que todos possam ver no slide e de forma “real” através da sua manipulação.
Propósito: Propiciar ao aluno, através da manipulação dos triângulos, a compreensão do conceito de congruência.
Discussão das Soluções

Tempo sugerido: 10 minutos (Slides 9 a 11).
Orientação: Como as descobertas já ocorreram durante a construção e manipulação da figura, espera-se que nesta parte haja a sistematização do que foi trabalhado ao longo da atividade, apresentando os estudantes a uma definição formal dos conceitos. Pode ser realizada leitura compartilhada, com manipulação das figuras de modo que todos possam ver no slide e de forma “real” através da sua manipulação.
Propósito: Propiciar ao aluno, através da manipulação dos triângulos, a compreensão do conceito de congruência.
Discussão das Soluções
Tempo sugerido: 10 minutos (Slides 9 a 11).
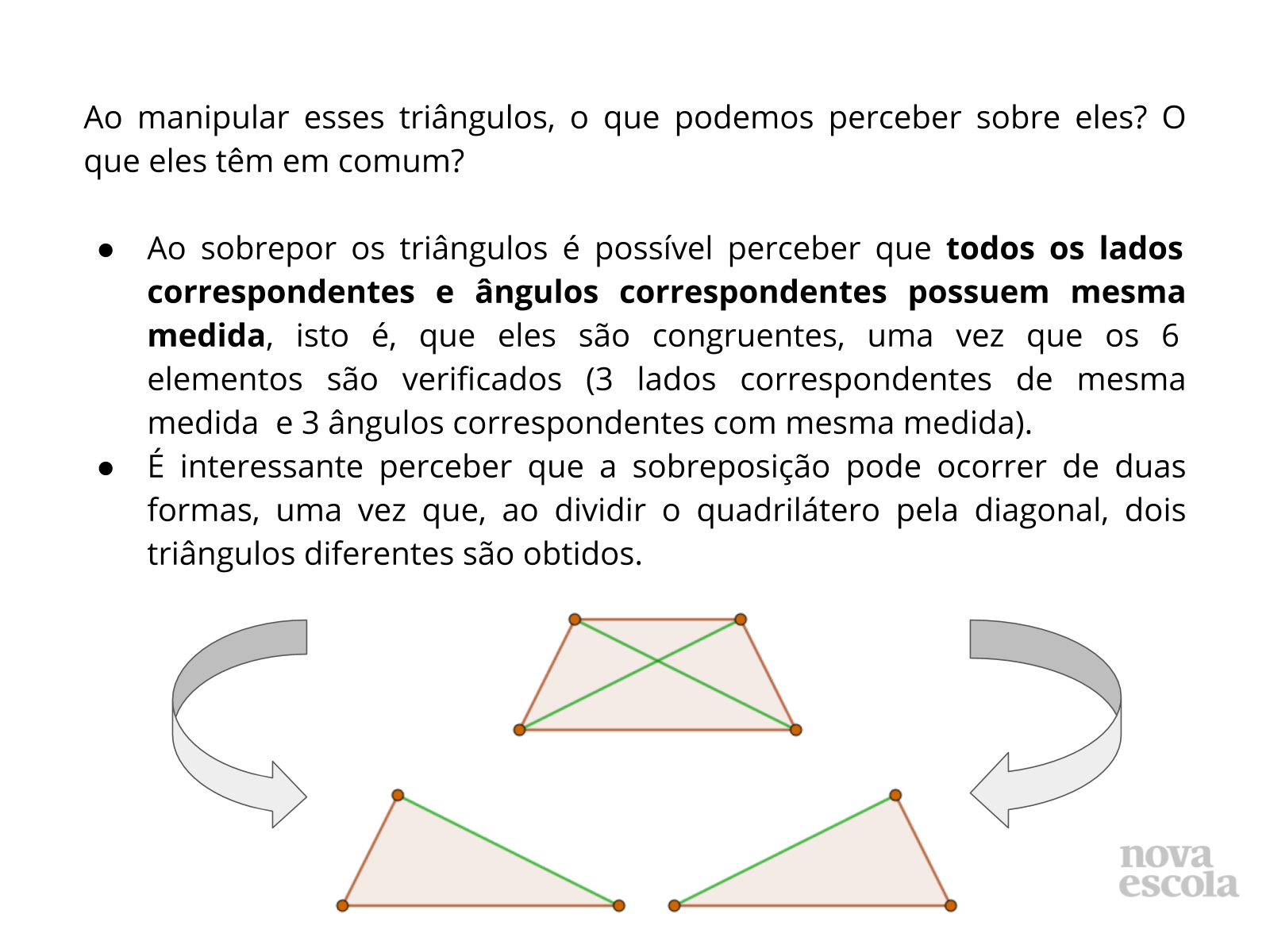
Orientação: Como as descobertas já ocorreram durante a construção e manipulação da figura, espera-se que nesta parte haja a sistematização do que foi trabalhado ao longo da atividade, apresentando os estudantes a uma definição formal dos conceitos. Pode ser realizada leitura compartilhada, com manipulação das figuras de modo que todos possam ver no slide e de forma “real” através da sua manipulação.
Propósito: Propiciar ao aluno, através da manipulação dos triângulos, a compreensão do conceito de congruência.
Sistematização do Conceito

Tempo sugerido: 2 minutos.
Orientação: Sistematize os principais conceitos aprendidos, interpretando-os junto com os alunos de modo que eles possam retomá-los sempre que necessário.
Propósito: Sistematizar o conceito central estudado no decorrer da aula.
Encerramento
Tempo sugerido: 3 minutos.
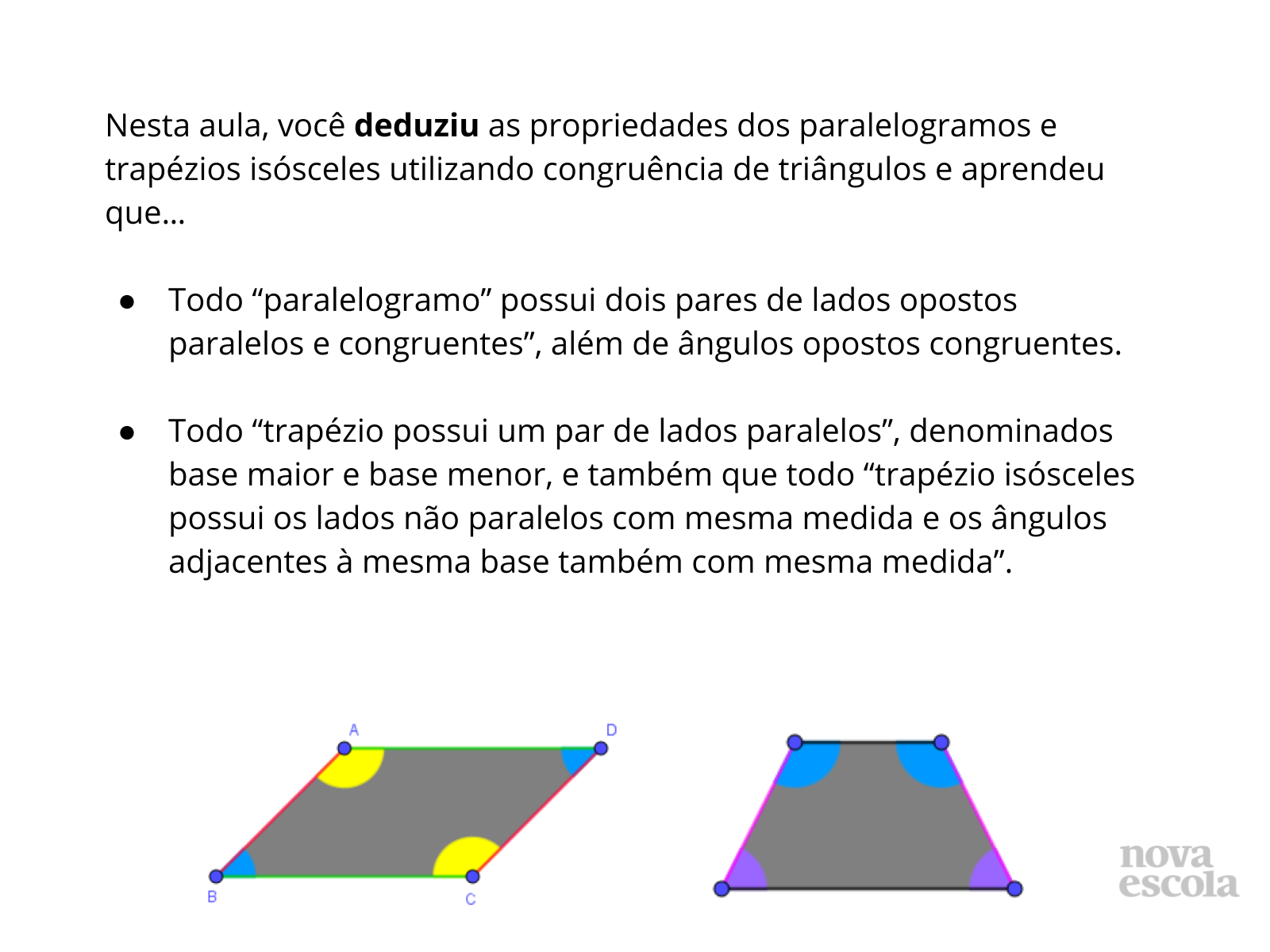
Orientação: Encerre a aula retomando com os estudantes as deduções por eles efetuadas, as quais descrevem as principais características dos paralelogramos e trapézios. Além disso, retome/relembre os questionamentos iniciais do Aquecimento para validar ou refutar as hipóteses levantadas e sugira que eles escrevam em seu caderno uma espécie de glossário, no qual as aprendizagens desta aula possam ser anotadas.
Propósito: Destacar, junto aos alunos, as principais características dos paralelogramos e dos trapézios.
Materiais Complementares:
Caso julgue necessário apresente aos estudantes as demonstrações formais. Você pode consultar aqui um material do site KhanAcademy que traz um pouco sobre elas.
Raio X
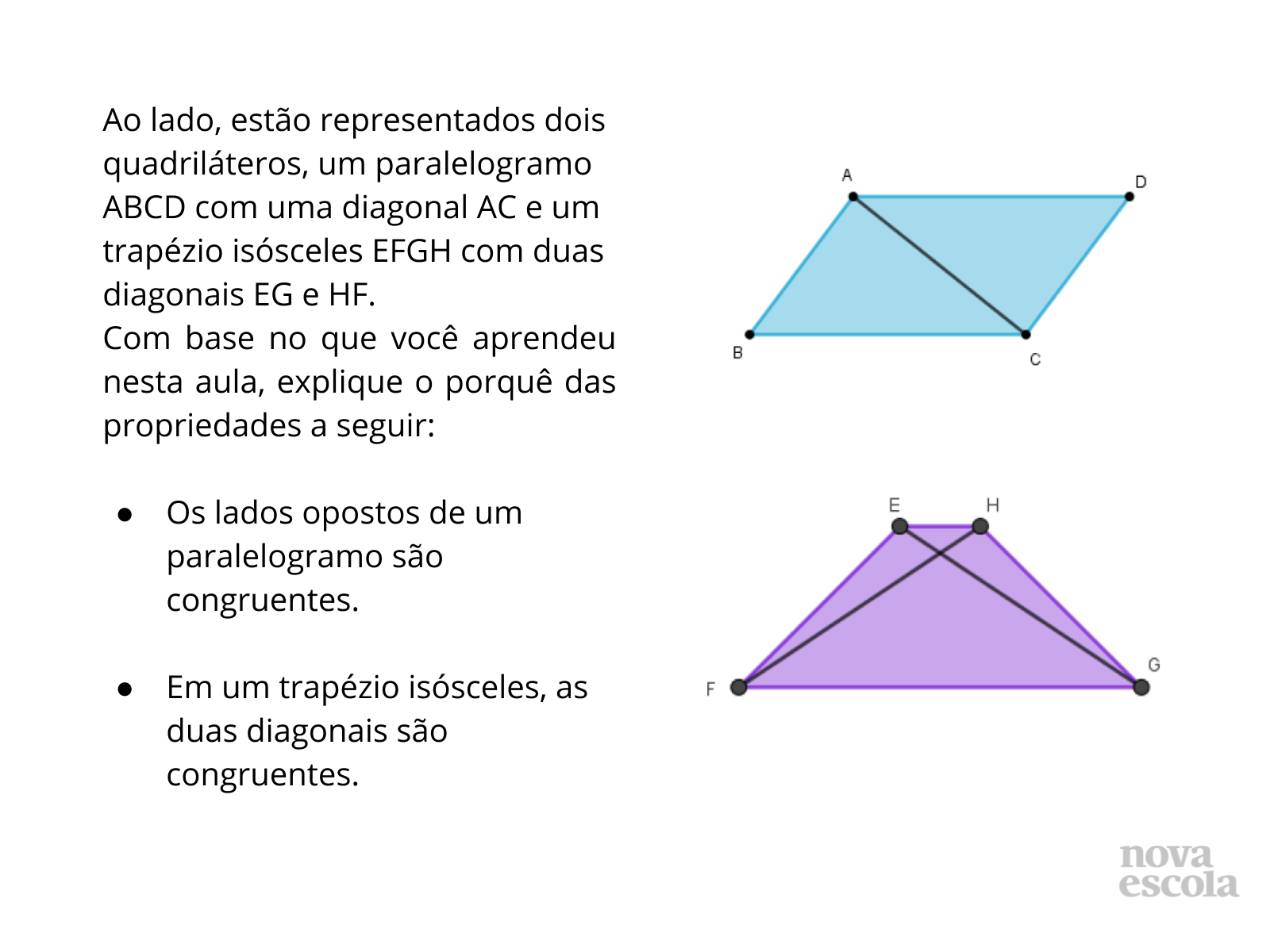
Tempo sugerido: 10 minutos.
Orientação: Realize uma leitura compartilhada ou individual do enunciado. Peça aos alunos que realizem a atividade individualmente e, em seguida, discutam com os colegas suas soluções com base no que foi apreendido.
Propósito: Verificar se o aluno justifica corretamente as principais propriedades presentes nos paralelogramos e trapézios.
Discuta com a turma:
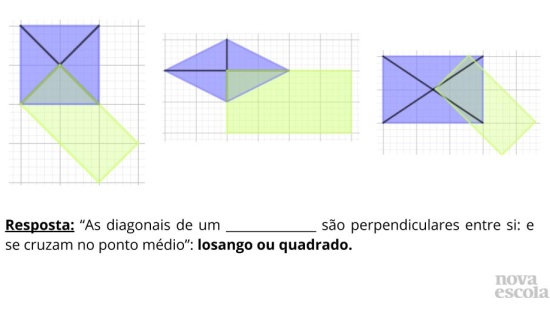
• Quais as propriedades utilizadas para chegar às afirmações?
• É possível recortar os quadriláteros e sobrepor as figuras para verificar tais propriedades?
• Você consegue notar a congruência de triângulos? Quais casos?
Materiais Complementares:
Sugestão de adaptação para ensino remoto
Código do plano
MAT8_16GEO01
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS
- Necessários: Papel, lápis, régua, esquadros, WhatsApp
- Opcionais: Messenger Sala de aluno ( https://www.messenger.com/groupcall/LINK:4svjhs7dyZw8zoxm/), Meet, Hangout, Zoom, plataforma da Khan Academy ( https://pt.khanacademy.org/)
Portal OBMEP ( https://portaldaobmep.impa.br/index.php/modulo/lista?serie=3)
Geogebra https://play.google.com/store/apps/details?id=org.geogebra&hl=pt_BR
Para este plano, foque na etapa ATIVIDADE PRINCIPAL (parte 2) + RAIO X
Aquecimento
O aquecimento traz apenas uma reflexão. Você pode usá-lo nas orientações.
Atividade principal
Na atividade há duas construções propostas: um paralelogramo e um trapézio isósceles. A construção é processual e exige conhecimentos geométricos na prática de tracejar figuras, utilizando instrumentos, bem como na linguagem matemática necessária para explicar as propriedades. Se sua turma não possuir tais habilidades, sugerimos que você grave um vídeo, seguindo a proposta de construção da atividade com o paralelogramo, por exemplo. Em seguida, você propõe, a construção do trapézio, e após discussão dessa etapa, a realização do Raio X. Faça a comunicação por WhatsApp ou em outra plataforma de comunicação como as indicadas nas Discussões. Mantenha um canal de comunicação permanente com sua turma e solicite que os alunos encaminhem as respostas da atividade para posterior discussão.
Sugestão: proponha um glossário aos alunos.
Na plataforma da Khan Academy há vários vídeos e demais recursos que tratam de quadriláteros. Você pode selecionar os materiais pertinentes e indicar aos alunos que possuem acesso à internet.
https://pt.khanacademy.org/math/geometry-home/quadrilaterals-and-polygons
No Portal da OBMEP há exploração dos elementos básicos da geometria plana (partes 1, 2 e 3) que pode servir de apoio aos alunos que possuem internet.
https://portaldaobmep.impa.br/index.php/modulo/lista?serie
Discussão das soluções
Essa proposta de atividade exige idas e vindas nas discussões. Assim, cada atividade proposta (Atividade principal, Raio X, atividades complementares) requer novas discussões para consolidação das aprendizagens. Retome as produções dos alunos para dar um feedback considerando os equívocos, acertos e dúvidas. Use informações do Encerramento e da Sistematização do conceito. No caso de construções geométricas, seria mais interessante que seu feedback fosse por meio de um vídeo curto, mas você pode optar por áudio ou registros escritos.
Se sua turma dispuser de ferramentas e internet, dê preferência por realizar as discussões em tempo real, por meio de uma das plataformas sugeridas abaixo. Se não tiver, use o WhatsApp que tem um alcance maior. Mas, não esqueça de manter um canal de comunicação para discussão e também de sugerir a realização das demais atividades desse plano (atividades complementares e Raio X).
Se for possível, você para discutir em tempo real, com sua turma. Use o Meet, Hangout ou Zoom e considere apenas os itens e os conceitos de maior relevância.
Você pode usar também o Messenger Sala de aluno https://www.messenger.com/groupcall/LINK:4svjhs7dyZw8zoxm/
Sistematização
Use nas orientações e/ou discussões
Encerramento
Use nas orientações e/ou discussões
Raio X
Use o Raio X como complemento à Atividade principal. Não esqueça também de propor a realização das atividades complementares.
Convite às famílias
xxxx
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Geisa Zilli Shinkawa da Silva
Mentor: Vinícius do Nascimento Silva Mano e Fabricio Eduardo Ferreira
Especialista de área: Priscilla Cerqueira
Habilidade da BNCC
EF08MA12 - Demonstrar as propriedades de quadriláteros por meio da identificação da congruência de triângulos.
Objetivos específicos
- Deduzir as propriedades dos paralelogramos utilizando congruência de triângulos;
- Deduzir as propriedades dos trapézios isósceles utilizando congruência de triângulos;
- Reconhecer as principais características dos quadriláteros e suas propriedades.
Conceito-chave
Propriedades de quadriláteros.
Recursos necessários
- Lápis de escrever, lápis de cor, borracha e tesoura;
- Esquadros e régua;
- Folha de papel A4 (para desenho e recorte);
- Atividades impressas em folhas ou projetadas.