Atividade principal
Plano de Aula
Plano de aula: Investigando Propriedades de Quadriláteros: Trapézio e Paralelogramo
Plano 2 de uma sequência de 10 planos. Veja todos os planos sobre Propriedades de quadriláteros
Tem interesse no tema "Neurociência, adolescências e engajamento nos Anos Finais"?
Inscreva-se neste tema para receber novidades pelo site e por email.
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Geisa Zilli Shinkawa da Silva
Mentor: Fabrício Eduardo Ferreira
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
EF08MA12 - Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
Objetivos específicos
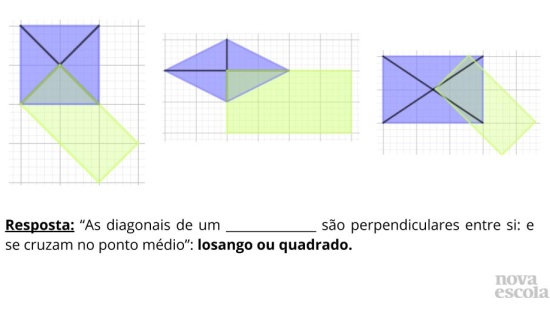
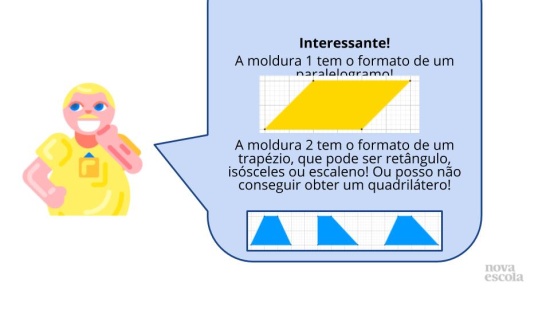
Investigar as propriedades dos paralelogramos, dos trapézios e trapézios isósceles, utilizando congruência de triângulos. Identificar as principais características dos quadriláteros e suas propriedades, além de reconhecer quadrados, retângulos e losangos como paralelogramos.
Conceito-chave
Propriedades de quadriláteros.
Recursos necessários
- Lápis de escrever, lápis de cor, borracha e tesoura;
- Esquadros e régua;
- Folha de papel A4 (para desenho e recorte);
- Atividades impressas (preferencialmente) ou projetadas.
Habilidades BNCC:
Objetivos de aprendizagem
Investigar as propriedades dos paralelogramos, dos trapézios e trapézios isósceles, utilizando congruência de triângulos. Identificar as principais características dos quadriláteros e suas propriedades, além de reconhecer quadrados, retângulos e losangos como paralelogramos.

Precisa de ajuda para criar uma aula personalizada?
Crie seu plano de aula em menos de um minuto no WhatsApp.
Novo curso gratuito

Conheça nosso mais novo curso sobre adolescências, neurociência e engajamento nos anos finais
VER CURSO