Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma. Argumente sobre a correlação dos temas estudados na Matemática, pois só poderemos compreender o que é complexo se entendermos o mais simples.
Propósito: Compartilhar o objetivo da aula.
Material complementar para impressão:
Referências bibliográficas para consulta
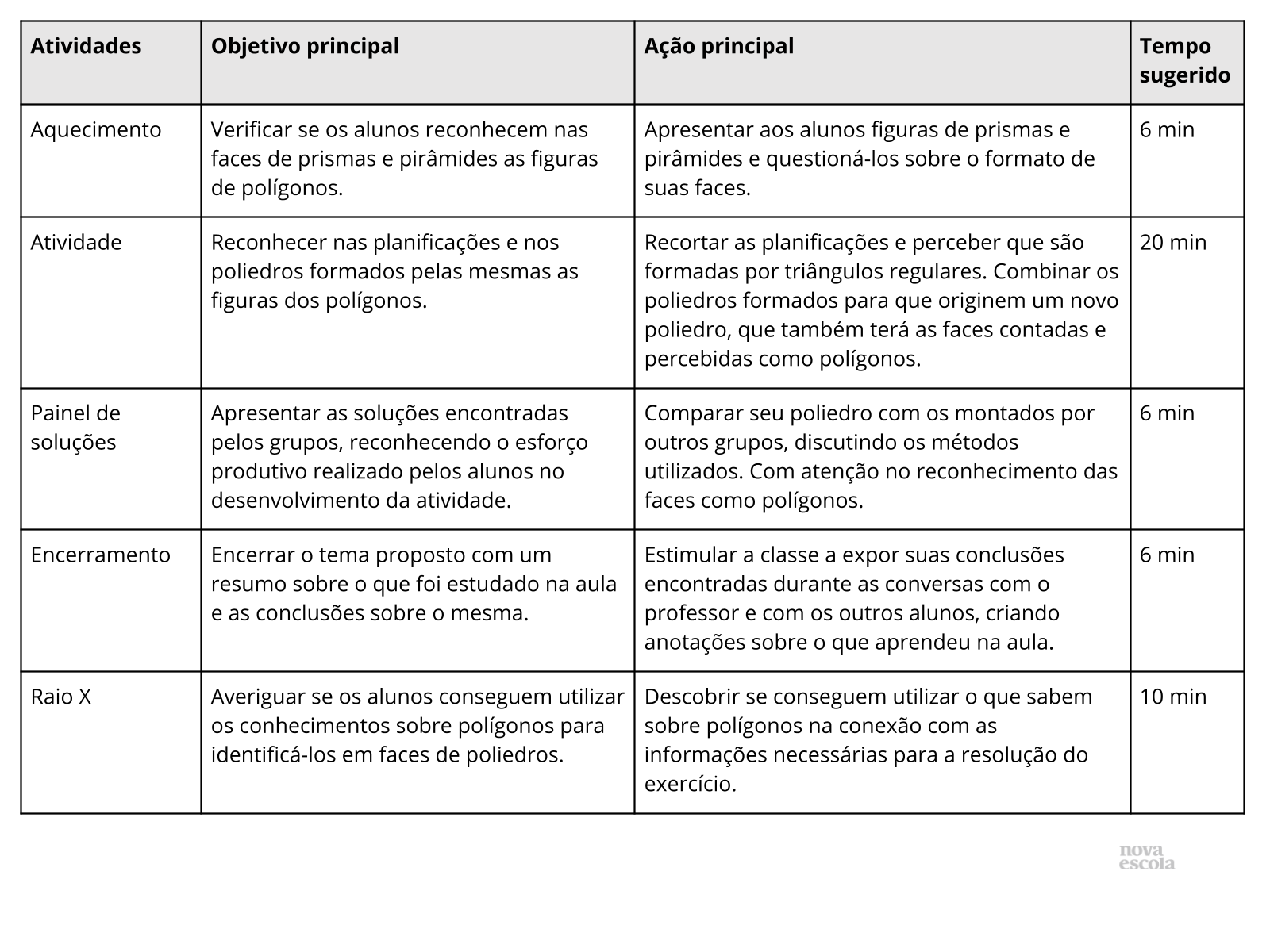
Aquecimento

Tempo sugerido: 2 minutos
Orientações: Você pode projetar as figuras. Mas seria preferível se a escola possui-se os modelos (em madeira), para os alunos manipularem os objetos.
Propósito: Resgatar o conhecimento sobre prismas e pirâmides como introdução ao tema principal.
Aquecimento (continuação)
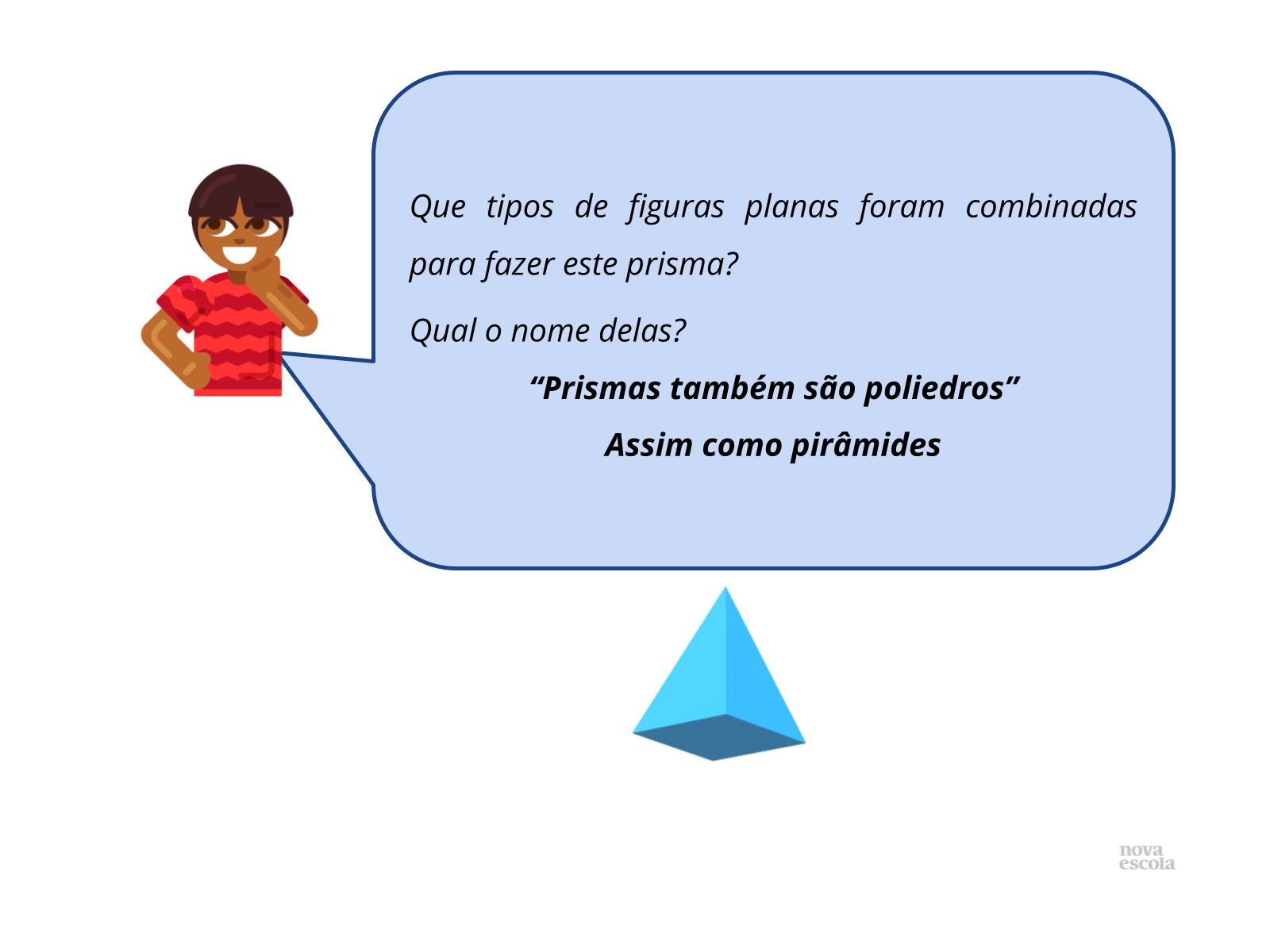
Tempo sugerido: 2 minutos
Orientações: Se os alunos responderem triângulos e retângulos, pergunte: E o que são essas figuras?
Converse com os alunos:
- Quais são as características dos poliedros?
Propósito: Resgatar o conhecimento sobre prismas e pirâmides como introdução ao tema principal.
Atividade principal

Tempo sugerido: 5 minutos
Orientação: Divida a classe em grupos e explique que irão construir um decaedro. Peça para juntarem as carteiras para facilitar a realização da atividade. Distribua uma cartolina para cada grupo, as 5 folhas (se o professor preferir trabalhar com figuras menores, pode reduzir a planificação, colocando mais figuras por folha) com a figura planificada, tesouras e cola. Atenção, cada grupo deve ter cinco planificações. A cartolina servirá para dar firmeza nos poliedros, mas se o professor considerar que não é preciso, o uso da mesma fica a seu critério.
Converse com a turma:
- Qual o nome do polígono da planificação?
- É um polígono regular?
- Depois de montado esse poliedro terá as características de suas faces?
- Que tipo de poliedro teremos?
Propósito: Trazer para a aula os conhecimento sobre polígonos, fazendo com que os alunos os percebam como faces dos poliedros que irão ser trabalhados.
Materiais complementares para impressão:
Atividade Principal
Resolução da Atividade Principal
Guia de Intervenção
Atividade principal
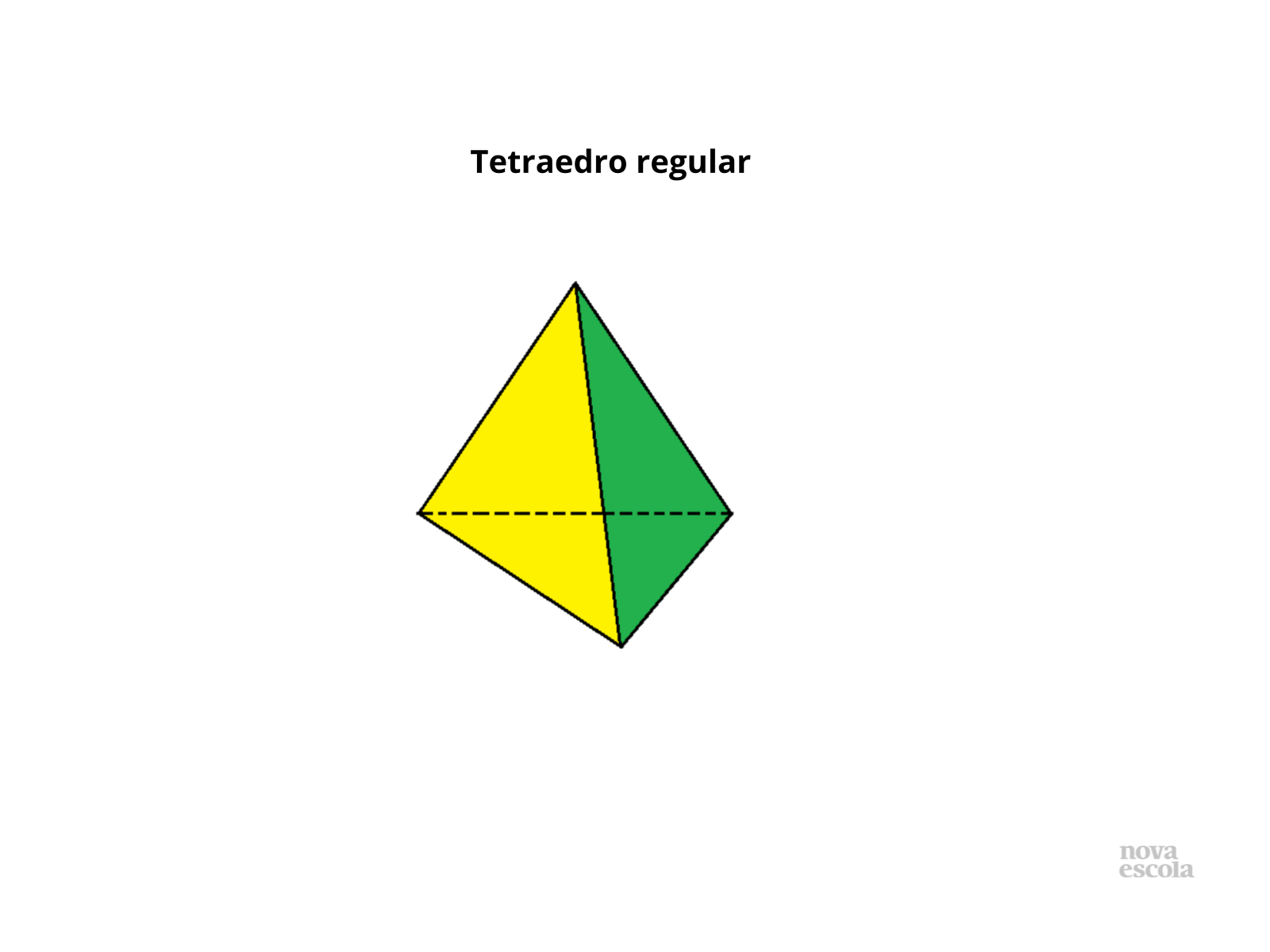
Tempo sugerido: 15 minutos
Orientação: Explique que devem recortar a planificação e colar a mesma na cartolina. Depois que fizerem isso com as cinco planificações, podem recortar da cartolina (no caso do professor ter optado pelo seu uso). Agora é só dobrar e colar as planificações, formando os tetraedros.
Converse com os grupos:
- Qual a razão desse poliedro se chamar tetraedro?
- Agora podem montar o “decaedro” usando os tetraedros.
“Não diga que o decaedro é um poliedro com dez faces”. Peça aos alunos para tentarem estabelecer uma comparação com os nomes dos polígonos, para descobrirem quantas faces deve possuir um decaedro.
Os grupos poderão usar a quantidade que quiserem de tetraedros para montarem o decaedro. Os tetraedros serão colados da maneira que os alunos julgarem a melhor para formar o decaedro.
Propósito: Estimular a criatividade do grupo em combinar os tetraedros de tal maneira que formem um decaedro.
Analisando as soluções

Tempo sugerido: 3 minutos.
Orientação: Como a atividade admite várias soluções, peça aos grupos para exporem o decaedro que montaram e que façam a contagem das faces do mesmo para confirmar que ele possui 10. Peça aos alunos que observem com atenção o decaedro que montaram, será que virando ele em outras posições não será possível perceber a imagem de outros polígonos? Apesar de todas as faces do decaedro ser um triângulo regular, se segurarmos o decaedro formado pela combinação de todos os tetraedros perceberemos a forma de um pentágono regular.
Discuta com a turma:
- Qual foi a principal dificuldade ao realizar a atividade?
- Usei todos os poliedros?
- Consigo perceber os polígonos nas faces dos poliedros?
- Se todas as faces do poliedro forem polígonos regulares, o poliedro também será regular?
Propósito: No momento em que contam as faces dos poliedros conseguem visualizar as mesmas como polígonos. E ao manusear o poliedro a procura de faces de outros polígonos e não encontram, pois ele é formado por tetraedros regulares, demonstra que entenderam que os polígonos serão as faces dos poliedros.
Analisando as soluções (continuação)
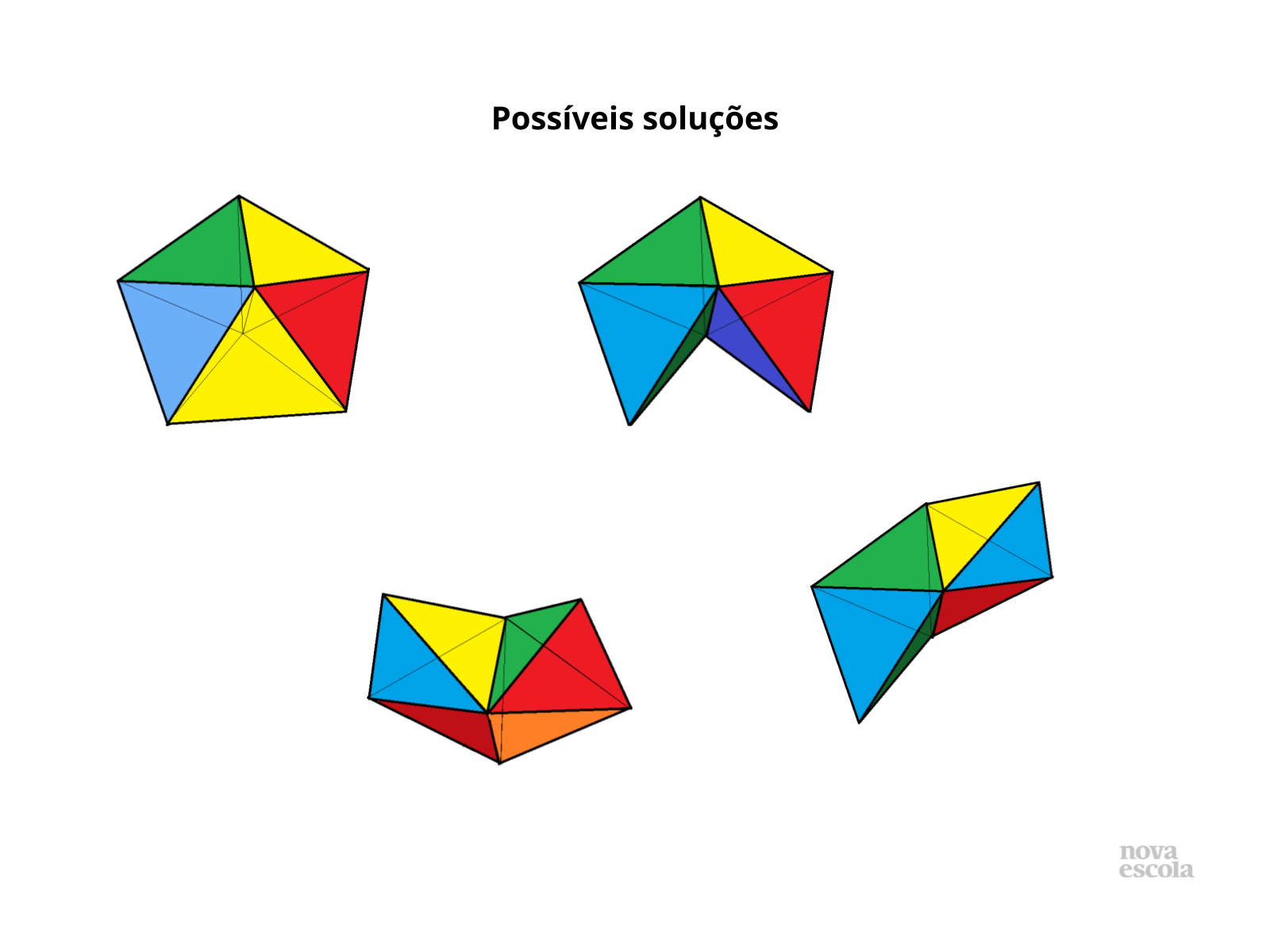
Tempo sugerido: 3 minutos.
Orientação: Neste slide temos as possíveis formações realizadas pelos alunos. Se o professor preferir fazer uma projeção, pode pedir que os alunos comparem seus modelos com os apresentados no slide. É interessante que percebam que as cores provavelmente estarão diferentes do slide, o que abrirá novos questionamentos sobre se o poliedro montado pelo grupo deve estar idêntico ao slide ou não para ser considerado “correto”.
Discuta com a turma:
- Qual foi a principal dificuldade ao realizar a atividade?
- Usei todos os poliedros?
- Consigo perceber os polígonos nas faces dos poliedros?
- Se todas as faces do poliedro forem polígonos regulares, o poliedro também será regular?
Propósito: No momento em que contam as faces dos poliedros conseguem visualizar as mesmas como polígonos. E ao manusear o poliedro a procura de faces de outros polígonos e não encontram, pois ele é formado por tetraedros regulares, demonstra que entenderam que os polígonos serão as faces dos poliedros.
Encerramento
Tempo sugerido: 6 minutos
Orientações: Questione os alunos sobre como são formados os poliedros. Peça para anotarem no caderno as conclusões obtidas durante a aula
Converse como os alunos:
- O objetivo da aula foi atingido?
- Conseguimos reconhecer os polígonos nas faces dos poliedros?
Propósito: Fazer com que os alunos compreendam que sem polígonos não existe poliedro. Reconhecer que a face ou a base de qualquer poliedro será um polígono.
Raio X
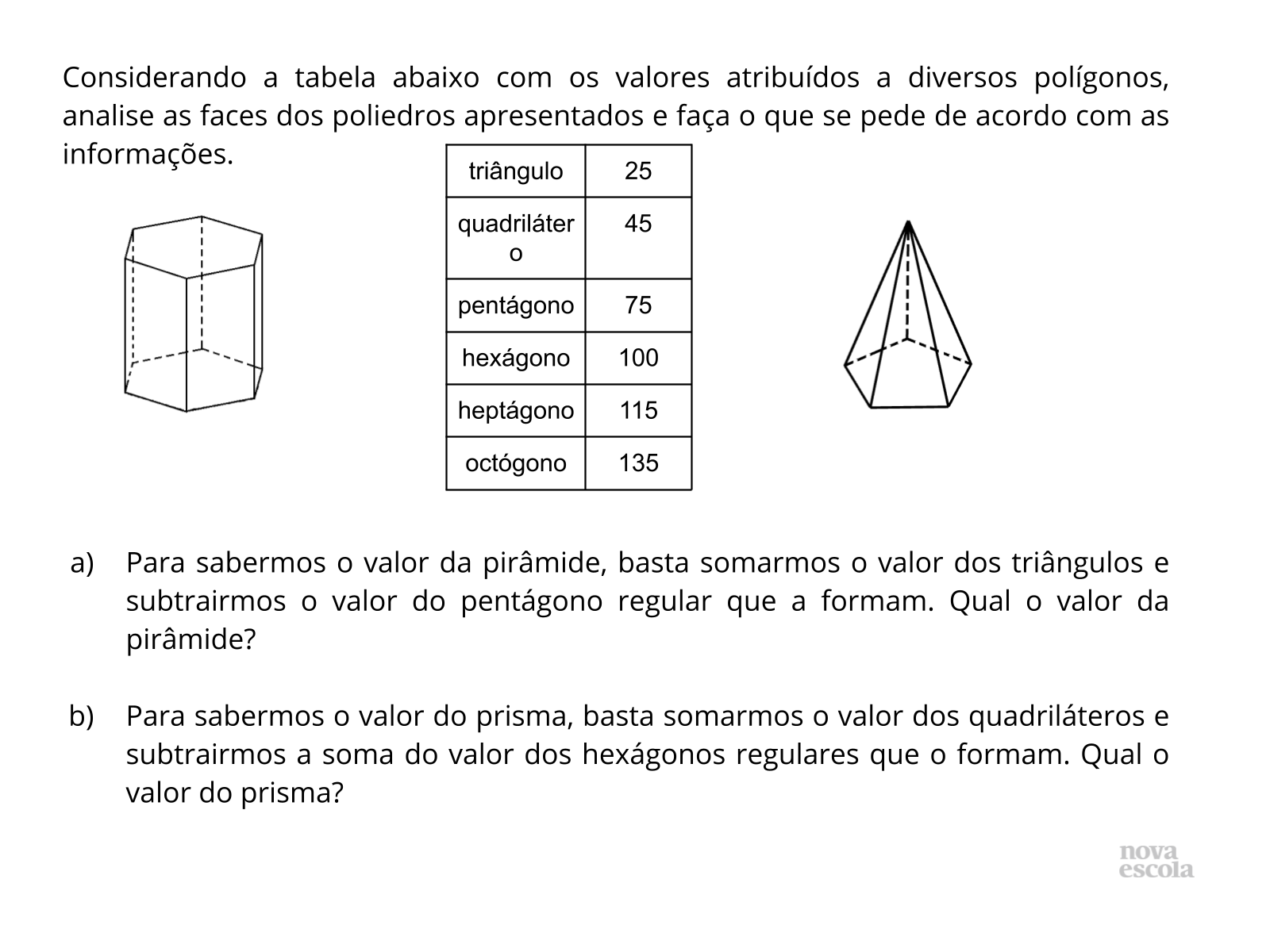
Tempo previsto: 10 minutos
Orientação: Diga que o exercício deverá ser feito individualmente. Distribua os exercícios impressos e explique que será feito com o objetivo de verificar se conseguem identificar os polígonos nas faces dos poliedros para conseguir realizar os cálculos.
Propósito: Constatar a assimilação do conteúdo pela análise da resolução individual do raio X.
Materiais complementares para impressão:
Atividade de Raio X
Resolução do Raio X
Atividade Complementar
Resolução da Atividade Complementar